改进的精英教学优化算法及其在甲醇合成优化中的应用
2017-10-14王应张凌波顾幸生
王应,张凌波,顾幸生
改进的精英教学优化算法及其在甲醇合成优化中的应用
王应,张凌波,顾幸生
(华东理工大学化工过程先进控制与优化技术教育部重点实验室,上海200237)
为了提高精英教学算法(ETLBO)的寻优能力,特别是精度差、寻优速度慢的问题,提出改进的精英教学算法。首先,通过自主学习过程,加强对优质解所在区域的局部勘探,提高算法的寻优效率。其次,引入“差异化帮扶”思想及自适应机制,对不同水平的学生施予适宜的、灵活的学习方式,有针对性的帮助,平衡了算法的勘探速度、精度。通过增加学生间的交流次数,提高了算法的全局勘探能力。标准函数优化结果表明,改进后的算法在寻优能力和勘探效率两方面都有明显提高。最后,建立甲醇合成的机理模型,将改进后的算法应用于甲醇合成过程的优化,取得了良好的效果。
算法;甲醇合成;精英教学算法;模型;优化
引 言
群体系统有着特定的规律性,由这些规律而启发出的群智能系统模型,正在被广泛地研究出来,如粒子群算法[1]、蚁群算法[2]、蜂群算法[3-6]等。教学算法是由Rao等[7]于2011年提出的一种源于对人类教学活动进行模拟的新型启发式算法。“教学算法”(teaching-learning-based optimization, TLBO)分为两个阶段:教学阶段,所有学生向老师学习,提高全体的成绩;学习阶段,学生间相互学习,提高个体成绩。
教学算法(TLBO)具有快速收敛、参数少等[8]优点,但处理复杂问题效果欠佳,学者们分别对其进行了不断的改进,如精英教学算法[9]、多目标优化[10-13]等,并广泛应用于工业问题中,如甲醇合成转化率软测量[14]、机械设计/优化[15-17]、无人机路径规划[18]、电网动态重构/调度[19-20]、数据聚类/分类[21-25]、优化工艺/参数[26-27]等。
甲醇是重要的有机化工原材料,广泛应用于有机合成、涂料和医疗应用等行业。甲醇合成过程的流程长、涉及变量多、非线性突出、各模块耦合性强且实际工况复杂多变,难以确定最佳的控制参数。将参数调节与最新的群智能算法结合,获得甲醇合成过程中优化参数,并实施,可以减少甲醇合成过程的损耗,降低企业的生产成本。
本文在精英教学算法(elitist TLBO, ETLBO)的基础上,针对精英教学算法寻优精度低、速度慢的问题,提出改进的精英教学算法(modified ETLBO, mETLBO)。通过引入自主学习,提高其寻优速度;采用差异化“帮扶”策略,平衡算法的勘探精度和速度。标准测试函数的测试结果,表明改进后算法具有良好的寻优能力。最后,应用于Lurgi管壳式副产蒸气甲醇合成过程的优化,并且在甲醇合成优化问题中取得了良好的效果。
1 精英教学算法
精英教学优化算法,分为教学阶段、学习阶段、精英策略3个阶段。每个学生的成绩为=(x,1,x,2, ,x,d),是总科目数。班级人数为,初始化为=+(-)r,、分别为成绩的上下限向量,r为0~1之间的随机数。选取最优的学生为下一次迭代中的教师。具体步骤为如下。
(1)教学阶段,全体学生向老师学习,其中班级、教学过程(次)分别为
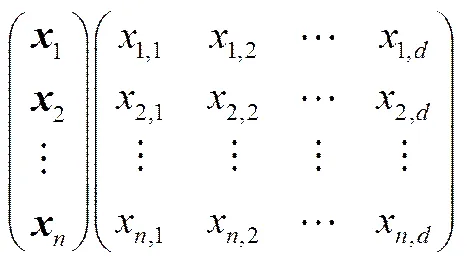
′=+r(X-×M) (2)
其中,X为最优个体(教师)的成绩,=round(1+r) 为教学因子,M为班级平均成绩;如果学习后的成绩更好,则更新,否则不变。
(2)学习阶段,对每个学生,如学生,随机选一个学生向其学习,迭代过程为

如果学习后的成绩更好,则更新,否则不变。
(3)精英策略
淘汰成绩差的学生,并用优秀的学生(精英解)替换。
2 改进的精英教学算法
由于ETLBO算法的寻优速度慢,精度差,亟需改进。在学习过程中,因为每个人的学习习惯、自我约束能力有差异,一部分学生能够利用闲暇时间进行自主学习。即优秀的学生通过自主学习,强化了学习效果,成绩提高得更快。在算法中引入此过程,由于较优解位于局部或全局最优的附近,通过加强对这些解所在区域的局部勘探,提高算法的寻优效率。
另外,对于成绩差的学生,采用“帮扶”策略,弥补落下的知识,使其成绩得以提高。差异化的“帮扶”策略可以针对不同水平的学生因材施教,给予学生差异化的学习指导,可以有针对性地帮助不同层次的学生弥补知识,提高其学习成绩。即对不同层次的个体,施以不同的迭代步长,一方面,可以维持种群的多样性,防止算法早熟;另一方面,可以防止算法陷入局部最优,增加了算法的稳定性。最后,增加学生之间的交流次数,分享知识,来提高学习者的成绩。在ETLBO算法的基础上,引入了上述的优化策略,具体如下。
2.1 自主学习
在学习过程中,优秀的学生在课后时间,自主学习各科知识,学习步长为
=(-) (4)
其中,为单位时间成绩提高率,如图1所示。根据幂律分布[28],学习过程中,前期投入单位时间成绩上升较快;反之,后期提高较慢。前期以较大的步长进行探索,提高算法的寻优速度,对于后期以较小的步长进行微细探索,而提高算法的精度。自主学习过程的伪代码如下所示。
初始化参数,自主学习人数1,科目数
//各科学习(维度方向探索)
for1 to n
for1to
//e为科目的轴向单位向量(维)
if(x+e)<(x) then′=x+e;
if(x-e)<(x) then′=x-e;end if
end
end
//整体复习
if(+r·(′-))<(′) then″=+r·(′-);end if
2.2 差异化“帮扶”策略
将班级学生按照成绩进行排序,并划分为A、B、C 3个等级。对低水平的学生,进行密切指导和督促,高强度的补差补缺;中等程度地进行适当的提醒和少量的查漏补缺;对于优秀的学生,给予自主学习的时间。根据学生的学习能力,有针对地精准化教学。算法运行中可以保留优秀学生的属性,可以有效地防止算法陷入局部最优及种群的早熟。其公式为
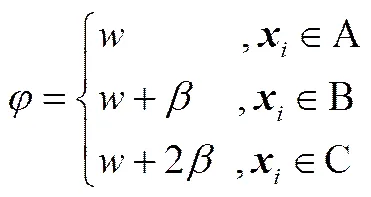
其中,为自适应步长,可以使算法可以灵活地适应最优值的波动,改善算法的全局寻优能力。
(6)
其中,1>2,;(·)为该次迭代的最优适应值;r为[0,1]间的随机数。适应值变化快时,学习步长加大,适应值变化慢时,学习步长变小,动态跟随并自适应调节,提高算法的灵活性。
将分级自适应因子代入式(2),可得改进后的教学公式为
′=×[+r(X-×M)] (7)
2.3 交流反馈
学习交流只发生在部分人之间,按照概率(rand),随机选学生通过提高交流次数,提高学习者的成绩。在两点间采样,遍历采样点,成绩提高则替代。通过增加随机的采样点,提高对空间的感知能力,增加算法的全局勘探能力。
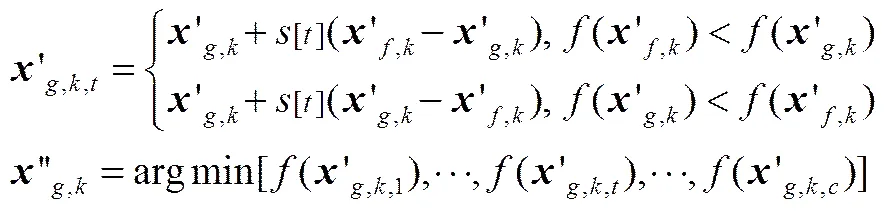
其中,=[r,r,…,r]为维随机采样矩阵。
(1)初始化班级,设置算法的参数;
(2)评价学生的适应度、记录精英解、划分等级;
(3)自主学习:选取优秀的学生,进行自主学习;
(4)教学阶段:采用式(7),对每个学生进行差异化教学;
(5)学习阶段:采用式(8),完成学生间的交流学习;
(6)精英解替换差解;
(7)满足条件,则终止,否则转步骤(2)。
为进一步规范县人大代表述职工作,10月11日,县人大常委会在城关街道组织召开县人大代表述职评议现场观摩会。县人大常委会主任、分管副主任和各镇人大主席、各街道人大工作室主任、各园(区)负责人大工作的同志参加了会议。观摩会上,住城关街道的6名县人大代表面对面向选区200多名选民代表作了述职报告。观摩会后,县人大常委会主任王晋成主持召开县镇人大代表述职评议工作动员部署会,要求各镇(街、园、区)人大认真学习此次观摩会,认真规范组织好代表述职活动,确保真述真评,不搞形式,不走过场,取得实效。
3 实验与分析
3.1 实验分析(一)
为了全面评价算法的性能,选取经典测试函数,如表1所示。为了评价算法处理不同复杂程度问题的能力进行20、30、50维测试,并与权威的算法ABC、I-ABC比较。为了客观评价,取相同的共性参数,种群规模为40,最大40000次适应度评价,运行50次。特性参数,1、2、分别为0.75、0.25、0.35,自主学习人数1、科目数、精英人数都设为3,ABC、I-ABC数据取至文献[29]。测试结果见表2,黑体表示算法寻得最优,精度为10-7。适应度曲线见图2。

表1 无约束测试函数
表2 优化结果对比

Table 2 Comparison of optimization results
(1)由表1可知,mETLBO算法在20、30、50维都寻得5次最优,且寻优精度非常高,优于其他算法。在50维复杂问题的处理上,改进后的算法也表现优异。此外,标准差的大小,反应算法的稳定性,其标准差也远小于ETLBO等算法的标准差,说明算法具有良好的稳定性。
(2)由图2可知,在单峰函数收敛上算法基本无差别,[图2(a)、(d)]。但是在多模函数测试表现上,改进后的算法可以快速寻得最优,尤其是处理高维复杂的问题,寻优速度明显好于其他算法[图2(e)~(g)]。
(3)因Ackley、Schwefel 、Rastrigin函数存在很多局部最优点和局部凹区域,由图2(c)、(e)、(f)、(g)可知,改进后的算法可以有效地跳出局部最优,而快速有效地寻得全局最优值,即mETLBO算法的全局搜索性能更好。
3.2 实验分析(二)
为确定mETLBO算法的特性参数,先进行正交实验,然后对结果进行显著性分析和时间复杂度分析。考虑实验(一)的结果,选择较为复杂的测试函数f5~f10,可以更加准确及客观地评价算法的性能。共性参数:为40,为30,为5,40000次适应度评价,精度10-7,独立运行50次。
(1)算法参数的确定
选取多模测试函数(f5~f10),分别进行正交实验、方差分析,旨在确定各个策略的最佳的参数配置。正交表设计为L12(28),改进的算法因子和水平参数见表3。分析结果见表4。
因方差分析中的显著性指标(sig)越小,表明该参数的改变其对结果影响越显著,故将参数影响按照权重大小次序排列,并由实验结果确定最佳的参数。根据表4,可得最终参数确定为3、3、0.75、0.25、0.35、10、0.7、4。
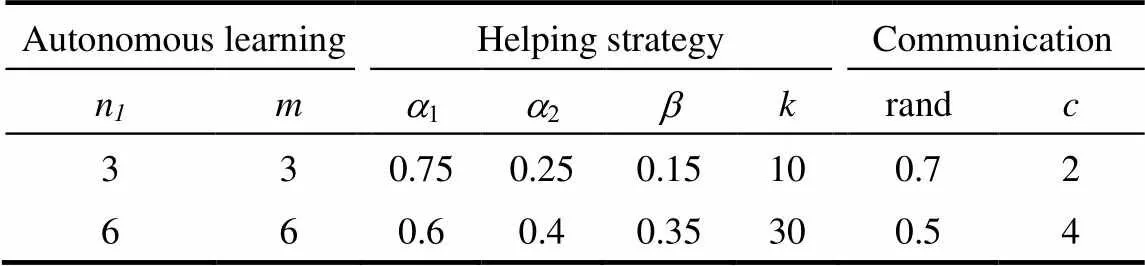
表3 正交因子、水平参数
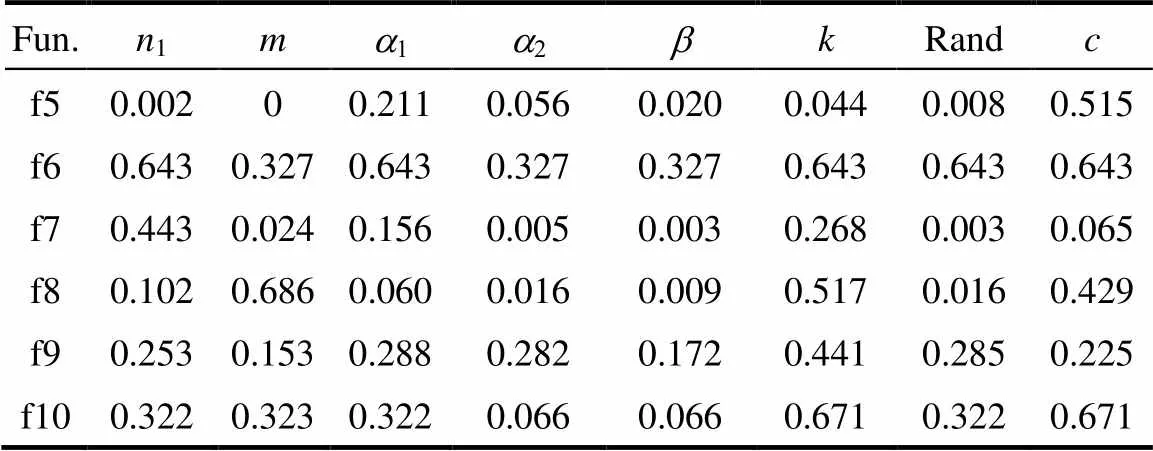
表4 正交实验-方差分析(sig)
(2)显著性检验及复杂度分析
根据正交实验中确定的参数,进行测试,并对结果进行显著性分析。即以ETLBO为对照组,进行Mann-Whitney显著性检验。结果见表5。同时进行算法时间记录,分析算法的运行效率,见表6。
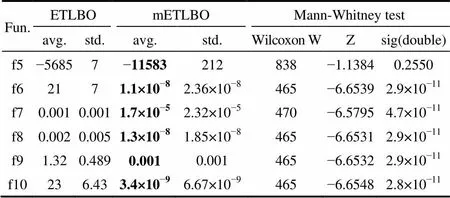
表5 实验测试结果
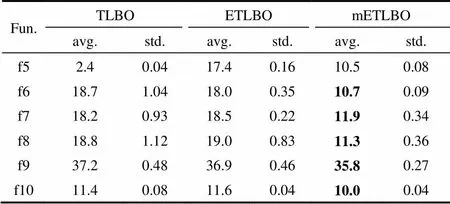
表6 运行时间统计
由表5可知,改进后的算法均明显优于精英教学算法,且根据Mann-Whiteny显著性检验,除f6不显著外,其余均小于0.05,显著性明显,改进后的算法最优适应值下降的速度较快,能够在相同适应度评价下,快速寻得最优值。
假设原算法有1个人向老师学习,共有个科目,则教师阶段为1次学习,学习阶段为21次学习,精英替代为2次,次循环的复杂度为[(1212)];改进后的算法则为[(1rand×2123)],3为自主学习次数;因为rand为交流概率,小于1,因此(ETLBO)>(mETLBO),改进后的算法时间复杂度较小,提高了算法的效率。mETLBO算法的时间复杂度更低,如表6所示,mETLBO算法运行时间均小于ETLBO。
(3)不同策略的对比
为分析3种策略的有效性及相互关系,分别将其单独加入到ETLBO算法上,测试函数(f5~f10),特性参数为正交实验的结果,维数为30。不同策略的迭代曲线如图3所示。
如图3(a)、(b)、(c)、(e)、(f)所示,mETLBO算法的寻优能力,总能够与最有效的策略保持一致性。说明策略间的相互影响较小,且通过混合所有策略可以使算法适用面更加广泛,提高了算法解决不同问题的能力。
4 甲醇合成优化应用
4.1 甲醇合成工艺及模型验证
甲醇是主要的化工有机的原材料,对其合成过程进行建模与优化至关重要。常见的甲醇合成工艺是Lurgi工艺,属于低压、铜基、等温反应工艺。其生产过程包括3个基本步骤:① 合成气的制备;② 合成气转化为甲醇;③ 甲醇的分离和纯化。针对Lurgi管壳式副产蒸气甲醇合成过程,采用文献[30]所述的C301铜基催化剂甲醇合成本征动力学方程,选择CO、CO2加氢为关键反应,CO、CO2为关键组分,建立甲醇合成过程的机理模型。其中,CO、CO2浓度随着床层高的变化为
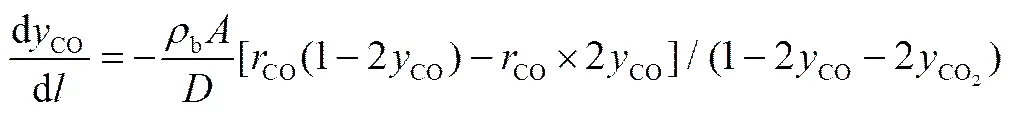
(10)
根据热量衡算,可得反应床温度随着床高的变化,为
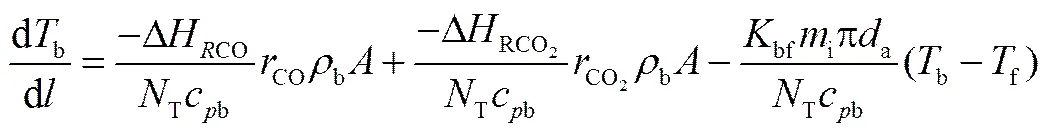
其中,CO、CO2分别为单位质量催化剂上的反应速率;b为床层堆积密度,为催化床横截面积。b、f分别为床层与管外介质温度,cb为混合物的摩尔热容;-DRCO、-DRCO2分别为CO、CO2加氢反应的热效应,T为催化床中混合气体的摩尔流量,bf、i、a分别为床层与冷却介质间的传热系数,反应管根数及反应管平均直径。
某Lurgi管壳式副产蒸气甲醇合成器,管长5800 mm,反应管尺寸44 mm×2 mm,共4309根。根据文献[31]的某厂2016年的实际生产数据的模型估计参数,建立实际工业模型。从生产报表中摘录5组数据进行模型验证,得到结果见表7。in是入塔温度,w是沸腾水温度。由结果可知催化床温度的分布,出塔的CO和CO2摩尔分数(CO、CO2)很好地贴合实际工业数据。

表7 模拟计算结果与工厂生产数据比较
4.2 甲醇合成的优化
甲醇合成中的各项生产控制因素,如反应压力、温度、循环气量等参数都影响甲醇合成回路中的能源消耗和物料消耗。在实际生产中,循环气量调节不恰当会使功耗增加,驰放气调节不当会增加物料消耗,即:(1)当加大循环气流量时,驰放气减小,但压缩机功耗也会增加,物料消耗减少,能源消耗增加;反之,减小循环气流量,压缩机功耗会减小,但驰放气的排放会增加,导致有效气体因排除而浪费。循环气流量与驰放气流量的关系[图4(a)];(2)随着循环气流量的不断增加,甲醇产量增加较快,但是循环气流量到一定值时,甲醇的产量则维持在某一稳定值[图4(b)]。此时,如果继续增加循环气流量,则会增加无效的压缩机功耗,增加了能源消耗,所以存在着物料消耗和能源消耗的优化问题。模型的新鲜气体积流量设为4×104m3·h-1,成分(体积分数)如表8所示。

表8 新鲜气成分
确定相应的优化目标,在一定新鲜气组分、流量、合成压力、管间水温度等条件下确定合适的循环气流量,使甲醇合成塔的生产单位甲醇所产生的功耗和物料消耗最低,即生产每单位甲醇所耗费的费用最低,为
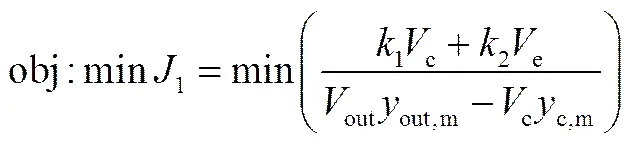
s.t.
(1)轴向浓度约束:式(9),式(10)
(2)轴向温度约束:式(11)
(3)循环气体积约束:3×105m3·h-1 (4)床层温度:240℃ (5)合成气温度:225℃<<255℃ (6)沸腾锅炉水压力:4.0~5.5 MPa 其中,1为1 m3循环气的压力经压缩机加压到入塔压力产生的能耗费用,1=38.4 kJ·m-3;2为1 m3驰放气的排放产生的物耗费用,2=4084.5 kJ·m-3;c为循环气的气体体积;e为驰放气的气体体积;out为出塔气的气体体积;out,m为出塔气中甲醇气体的百分比;c,m为循环气中甲醇气体的百分比。 将目标函数带入算法中,参数与正交实验所确定的参数相同,进行优化,寻优结果见表9。 表9 甲醇合成优化结果 由图5可知,改进后的算法可以有效优化甲醇合成中的循环气流量和H/C等参数,且适应度下降较快,寻得的甲醇单耗更低。由表9可知,在给定新鲜气流量及成分情况下,以甲醇单耗最低为目标时,合成塔压力为4.2 MPa,循环气流量应控制为4.7927×105m3·h-1,此时甲醇产量为380.3 kmol·h-1;合成塔压力为4.3 MPa,循环气流量应控制为5.1586×105m3·h-1,此时甲醇产量为385.8 kmol·h-1。 本文提出了一种改进的精英教学算法,主要进行了3个方面的改进: (1)引入自主学习过程,加强了优质解对其所在区域的局部勘探; (2)引入差异化帮扶策略; (3)设计了步长自适应及差异化自适应策略,平衡算法的综合性能,并分析不同参数对算法性能的影响。测试函数结果揭示出自主学习、差异化帮扶、自适应策略可以有效提高算法性能。最后,应用于甲醇合成过程的优化,能够有效降低甲醇合成回路的能源和物料消耗,提高了经济效益。 [1] KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. 1995, 4: 1942-1948. [2] MANIEZZO D M, COLORNI V A. The ant system: optimization by a colony of cooperating agents[J].IEEE Trans. on Systems, Man, and Cybernetics B, 1996, 26(1): 29-41. [3] AKAY B, KARABOGA D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192(1): 120-142. [4] BANHARNSAKUN A, ACHALAKUL T, SIRINAOVAKUL B. The best-so-far selection in artificial bee colony algorithm[J]. Applied Soft Computing, 2011, 11(2): 2888-2901. [5] WU B, QIAN C H. Differential artificial bee colony algorithm for global numerical optimization[J]. Journal of Computers, 2011, 6(5): 841-848. [6] CHEN S M, SAROSH A, DONG Y F. Simulated annealing based artificial bee colony algorithm for global numerical optimization[J]. Applied Mathematics & Computation, 2012, 219(8): 3575-3589. [7] RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303-315. [8] SATAPATHY S C, NAIK A. Modified teaching-learning-based optimization algorithm for global numerical optimization—a comparative study[J]. Swarm & Evolutionary Computation, 2014, 16: 28-37. [9] RAO R V, PATEL V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J].Int. J. Ind. Eng. Comput., 2012, 3(4): 535-560. [10] PATEL V, SAVSANI V. Multi-objective optimization of a stirling heat engine using TS-TLBO (tutorial training and self learning inspired teaching-learning based optimization) algorithm[J]. Energy, 2016, 95: 528-541. [11] RAJA B D, JHALA R L, PATEL V. Multi-objective optimization of a rotary regenerator using tutorial training and self-learning inspired teaching-learning based optimization algorithm (TS-TLBO)[J]. Applied Thermal Engineering, 2016, 93: 456-467. [12] PATEL V K, SAVSANI V J. A multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)[J]. Information Sciences, 2016, 357: 182-200. [13] SIVADURGAPRASAD C, KOMMADATH R, KOTECHA P. A note on multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)[J]. Information Sciences, 2016, 373: 337-350. [14] 双翼帆, 张凌波, 顾幸生.基于高斯过程和改进教与学优化算法的甲醇合成转化率软测量[J]. 华东理工大学学报(自然科学版), 2016, (3): 369-374. SHUANG Y F, ZHANG L B, GU X S. Soft sensor of conversion rate in methanol synthesis based on Gaussian process and improved teaching-learning-based optimization[J]. Journal of East China University of Science and Technology(Nature Science), 2016, (3): 369-374. [15] TOĞAN V. Design of planar steel frames using teaching-learning based optimization[J]. Engineering Structures, 2012, 34: 225-232. [16] CAMP C V, FARSHCHIN M. Design of space trusses using modified teaching-learning based optimization[J]. Engineering Structures, 2014, 62: 87-97. [17] DEDE T, AYVAZ Y. Combined size and shape optimization of structures with a new meta-heuristic algorithm[J]. Applied Soft Computing, 2015, 28: 250-258. [18] 武巍, 邹杰. 基于改进教-学算法的无人机航路规划[J].计算机应用, 2016, 36(9): 2626-2641. WU W, ZOU J.Route planning method for unmanned aerial vehicle based on improved teaching-learning algorithm[J]. Journal of Computer Applications, 2016, 36(9): 2626-2641. [19] 时慧喆, 刘志鹏, 钟文强. 基于混合优化算法的配电网动态重构研究[J].电气技术, 2016, 17(6): 41-46. SHI H Z, LIU Z P, ZHONG W Q. The research for dynamic distribution network reconfiguration based on hybrid optimization algorithm[J]. Electrical Engineering, 2016, 17(6): 41-46. [20] MANDAL B, ROY P K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization[J]. International Journal of Electrical Power & Energy Systems, 2013, 53: 123-134. [21] SATAPATHY S C, NAIK A. Data Clustering based on teaching-learning-based optimization[C]// International Conference, Semcco, Visakhapatnam, Andhra Pradesh, India, December. DBLP, 2011: 148-156. [22] SAHOO A J, KUMAR Y. Modified Teacher Learning Based Optimization Method for Data Clustering[M]//Advances in Signal Processing and Intelligent Recognition Systems. Springer International Publishing, 2014: 429-437. [23] NAIK B, NAYAK J, BEHERA H S,. A self adaptive harmony search based functional link higher order ANN for non-linear data classification[J]. Neurocomputing, 2016, 179: 69-87. [24] PANIGRAHI S K, PATTNAIK S. Empirical study on clustering based on modified teaching learning based optimization[J]. Procedia Computer Science, 2016, 92: 442-449. [25] MURTY M R, NAIK A, MURTHY J V R,. Automatic clustering using teaching learning based optimization[J]. Applied Mathematics, 2014, (5): 1202-1211 [26] VENKATA RAO R, KALYANKAR V D. Parameter optimization of machining processes using a new optimization algorithm[J]. Materials and Manufacturing Processes, 2012, 27(9): 978-985. [27] RAO R V, KALYANKAR V D. Parameter optimization of modern machining processes using teaching-learning-based optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 524-531. [28] ANDRIANI P, MCKELVEY B. From Gaussian to Paretian thinking: causes and implications of power laws in organizations[J]. Organization Science, 2009, 20(6): 1053-1071. [29] LI G, NIU P, XIAO X. Development and investigation of efficient Artificial Bee Colony algorithm for numerical function optimization[J]. Appl.Soft Comput., 2012, 12(1): 320-332. [30] 谢克昌, 房鼎业.甲醇工艺学[M]. 北京: 化学工业出版社, 2010: 175-195. XIE K C, FANG D Y. Methanol Technology[M]. Beijing: Chemical Industry Press, 2010: 175-195 [31] 俞灵杰, 张凌波, 顾幸生. 基于改进狼群算法的甲醇合成塔转化率机理建模及参数估计[J]. 华东理工大学学报(自然科学版), 2017, (5), 待发表. YU L J, ZHANG L B, GU X S. Mechanism modeling and parameter estimation of conversion rate in methanol synthesis tower based on improved wolf pack algorithm[J]. Journal of East China University of Science and Technology(Nature Science), 2017, (5), in press. Application of modified elitist teaching-learning-based optimization algorithm to process optimization of methanol synthesis WANG Ying, ZHANG Lingbo, GU Xingsheng (Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China) Elitist teaching-learning-based optimization (ETLBO) algorithm is inspired by practical teaching-learning process. A novel group search optimizer, modified elitist teaching-learning-based optimization (mETLBO), was proposed to improve low precision and poor stability of the ETLBO. First, an autonomous learning process was introduced to strengthen local search of high quality solution so as to improve algorithm’s elite-searching speed. Second, differentiated support and self-adaptive strategy providing appropriate and flexible learning approach to students at various levels, were applied to offer desirable assistance and balance searching rate and accuracy of the algorithm. Third, global searching ability of the algorithm was enhanced by increasing communication frequency between students. Optimization results on standardized functions show that the proposed algorithm is obviously superior to the original one in performance and efficiency. Finally, satisfactory results were achieved by applying the improved algorithm to process optimization with mechanism model of methanol synthesis. algorithm; methanol synthesis; ETLBO; model; optimization 10.11949/j.issn.0438-1157.20170146 TP 273 A 0438—1157(2017)08—3141—11 张凌波。第一作者:王应(1993—),男,硕士研究生。 国家自然科学基金项目(61573144)。 2017-02-16收到初稿,2017-04-19收到修改稿。 2017-02-16. ZHANG Lingbo, zlb@ecust.edu.cn supported by the National Natural Science Foundation of China (61573144).
5 结 论
References
