基于多证据融合决策的间歇过程测量数据异常检测方法
2017-10-14刘伟旻王建林邱科鹏于涛赵利强
刘伟旻,王建林,邱科鹏,于涛,赵利强
基于多证据融合决策的间歇过程测量数据异常检测方法
刘伟旻,王建林,邱科鹏,于涛,赵利强
(北京化工大学信息科学与技术学院,北京 100029)
间歇过程测量数据的高维、非线性、非高斯分布特征直接影响过程测量数据异常检测的准确性,为了融合多源数据异常检测信息,提升间歇过程测量数据异常检测精度,提出了一种基于多证据融合决策的间歇过程测量数据异常检测方法,该方法通过引入证据理论(Dempster-Shafer,D-S),采用主焦元判别伪证据和重新计算证据权重改进冲突证据处理方法,减小了冲突证据对多证据融合决策结果的影响,提高了间歇过程测量数据异常检测的准确率。构建了基于多证据融合的测量数据异常检测模型并将其应用到间歇过程测量数据异常检测决策判决中。实验结果表明,该方法能够融合多证据信息,有效地处理冲突证据,实现了间歇过程测量数据异常检测,降低了误检和漏检率。
间歇过程;D-S证据理论;冲突证据;多证据决策;测量数据异常检测
引 言
间歇过程作为工业生产中的一种重要生产方式,被广泛应用于精细化工、生物制药、食品、聚合物反应及金属加工等现代重要生产领域[1-3]。间歇过程在线检测技术及系统的不断进步,提供了丰富的过程测量数据,为过程在线监测与优化控制提供了基础和保障[4-7]。然而间歇过程现场检测仪表及系统出现性能衰减、故障、外界干扰等异常,直接导致过程测量数据的可靠性和准确性降低,严重影响过程测量数据的质量[8],因此实现对间歇过程测量数据异常检测,能够有效地保障过程在线监测、优化控制等方法和技术的实施[9-10]。
传统的过程数据异常检测方法主要是利用误差的显著性水平进行统计假设检验,包括整体检验法、约束检验法、组合检验法、广义似然比法等[11],这些方法主要应用于有明确过程模型约束的过程测量数据异常检测上,虽然取得了较好的应用效果,但适用面较窄,难以在过程机理复杂的间歇过程测量数据异常检测中应用。近年来出现了基于数据驱动的过程测量数据异常检测方法:聚类分析、多变量统计分析等方法[12]。聚类分析方法[13]不依赖过程模型,能够实现过程测量数据异常检测。田慧欣等[14]将聚类算法与软测量建模过程相结合,用建模误差指导过失误差侦破过程,使其克服了单纯聚类分析的缺陷。但聚类分析提取特征量单一,难以全面表达复杂的过程测量数据异常。多变量统计分析方法[15]以采集到的过程测量数据为基础,依靠分析数据统计量,从其中的变化提取特征,挖掘隐含的过程测量数据异常信息。Narasimhan等[16]根据间歇过程测量数据的时变信息,通过建立统计分析模型实现间歇过程测量数据异常检测,该方法从不同侧面反映测量数据异常变化信息,但容易忽略某个维度的异常变化特性,无法保证多变量统计分析结果的准确性,容易导致误检;Luo等[17]同时考虑多个维度上的时变数据特征的变化,实现全局多变量统计分析,获得了表征过程测量数据异常的统计量变化,但其忽略局部微小变化信息,容易导致漏检。基于数据驱动的方法均采用单一过程测量数据异常检测获取单源数据异常信息,没有通过多源数据异常信息融合处理来提高间歇过程测量数据异常检测的准确率。
证据理论(Dempster-Shafer,D-S)是一种不确定性推理方法[18],通过对多源证据的一致性信息处理,排除和整合矛盾信息,从不精确和不完整信息中得到可能性最大的结论,并已在故障检测与诊断中得到应用,取得较好的应用效果。陈斌等[19]将神经网络和证据理论相结合,对管道流量、压力、声波传感器等局部决策信息进行证据融合,提高了管道泄漏检测精度;Ghosh等[20]在不同层次上提取连续搅拌反应器的多源诊断结果,使用D-S证据理论融合多源信息,提高异常检测精度;Hui等[21]提出一种SVM-DS方法,利用证据融合改进SVM轴承多类异常检测投票模型,实现在证据混乱下的异常检测。将证据融合理论引入间歇过程测量数据异常检测,融合多源测量数据异常证据信息,是提高间歇过程测量数据异常检测准确率的有效途径。然而当多源证据体间不完全一致时,将出现冲突证据处理问题,直接影响证据融合结果的准确性。
本文提出了一种基于多证据融合决策的间歇过程测量数据异常检测方法。引入D-S证据理论,采用主焦元判别伪证据和重新计算证据权重,改进冲突证据处理方法,构建了基于多证据融合的测量数据异常检测模型,并将其应用到青霉素发酵过程测量数据异常检测决策判决中,验证所提方法的有效性。
1 改进的冲突证据处理方法
1.1 证据理论及冲突证据
D-S证据理论是一种不确定性问题处理方法,能够将信度赋予假设空间的单个元素,同时也能赋予它的子集[22]。定义识别框架是所有可能取值的一个完备集合,且内的元素是互不相容的。在上的基本概率分配(basic probability assignment,BPA)是一个2®[0,1]的函数,即BPA函数,且满足()=0,及
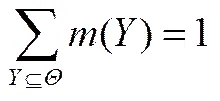
式中,使得(>0的称为焦元,表示识别框架中的任一子集。()为命题的支持程度。对于上的任一焦元,若由2条证据体获取的BPA为1,2,其焦元分别为和,则2条证据的融合规则为
(2)
式中,为冲突系数;1/(1-)为归一化系数;通过归一化处理将大小为的信度分配给非空集。证据融合后的不确定度为

实际应用中,当证据源受到某种较大干扰时,将提供错误的信息,产生伪证据,伪证据与其他证据源提供的证据产生高度冲突,出现冲突证据问题。当直接利用D-S规则进行证据融合将产生相悖的结论[23];即使有大量的有效证据,融合后得到正确的结论,然而由于伪证据的影响,导致收敛速度慢,甚至使目标命题的信度支持不突出,直接影响决策。
1.2 改进的冲突证据处理方法
证据推理的期望是增强主焦元的置信度,Murphy方法使平均支持程度最高的焦元获得最终支持[24]。本文提出了采用主焦元判别伪证据和权重计算对冲突证据进行处理,即由Murphy方法求出平均证据并确定主焦元,引入权重计算,计算主焦元的大小并确定伪证据。若存在伪证据,则修改证据源;若不存在伪证据,各证据支持的命题一致,直接用D-S融合证据。
改进的冲突证据处理步骤如下。
(1)判断证据体数量,若仅有2条证据融合,默认两个证据的权重为0.5,转入步骤(5)。
(2)由Murphy方法求出平均证据的m= [1,2,…,a],由max(1,2,…,a) 确定主焦元的大小,对应命题标号为。若主焦元不唯一或者主焦元的大小等于或小于证据支持命题的不确定度的值,则说明证据间整体冲突较大,转入步骤(3);否则转入步骤(6)。
(3)判断是否存在伪证据,即提供错误决策信息的证据体。各证据对主焦元位置命题的支持度为m(a),若存在m(a)<,且m(a)≠max(m[1,2,…,a])则判定证据体为伪证据,转入步骤(4);否则,转入步骤(6)。
(4)利用对主焦元的支持度确定各证据权重w,即
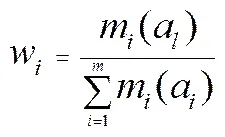
(5)对证据进行加权平均
(5)
利用D-S组合规则融合加权后的证据-1次,得到最后组合结果,转入步骤(7),为证据数。
(6)利用D-S方法对证据进行合成,得到最终结果。
(7)根据决策规则做出决策。
该改进的冲突证据处理方法能将冲突证据的判别和处理同时进行,由证据体入手,根据期望命题判断冲突证据,与应用对象无关,具有普适性。判别冲突证据时只进行简单的比较运算,具有运算量小的优点。基于主焦元确定权重系数,从期望命题出发,意义明确,即与其他多数证据信息较为一致的证据,其可信度高,其权重较大,反之则较小。
2 基于多证据融合决策的间歇过程测量数据异常检测
2.1 多证据融合决策的间歇过程测量数据异常检测模型
图1为多证据融合决策的间歇过程数据异常检测模型,由数据预处理模块、多证据构造模块、多证据融合推理分析模块、融合决策模块组成。在使用间歇过程数据进行过程建模监测前,间歇过程三维矩阵()按照批次方向或变量方向展开为二维矩阵()或(),其中为批次个数,为变量个数,为采样时间,并进行相应的标准化处理,使用多元统计分析方法提取反映过程测量数据异常的统计量特征信息,构造证据体子空间。将每个证据体在征兆空间进行初步诊断,获得各证据体的BPA,并通过多证据融合进行决策,最终实现间歇过程数据异常检测。
2.2 基于统计量特征多证据构造
在上述数据标准化处理的基础上,获得两种标准化后的数据,分别使用多向主元分析法[25](multiway principal component alalysis,MPCA)和平行因子法[26](PARAFAC2)方法求得在不同置信度下的预测误差平方和指标(squared predition error,SPE)和Hotelling-2(下文简称2)统计量的测量数据异常检测结果。
(1)基于MPCA的统计量特征多证据构造
MPCA将三维数组展开为二维数据形式后,计算相应的得分矩阵、负载矩阵及其残差矩阵,并保留适当的主元个数,MPCA模型定义如下
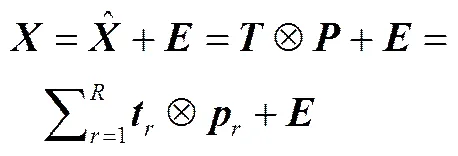
其计算出来的主成分可近似地服从正态分布。
①SPE特征证据源:MPCA模型的SPE统计量服从加权2分布

其中,m是建模数据集中所有间歇过程批次数据在第个采样时刻SPE(=1,…,)值的均值;v则是对应的方差。在离线或在线计算时刻的SPE值时,的计算如下
(8)
②2特征证据源:MPCA模型的2统计量服从多维正态分布

其中,-1是建模数据集的协方差对角阵,表示在第个采样时刻的得分向量。在离线或在线计算时刻的2值时,的计算如下
=P(10)
根据不同的显著水平,根据式(7)和式(9)能够获得不同置信度下SPE和2控制限用于在线监测。
(2)基于PARAFAC2的统计量特征多证据构造
将PARAFAC2用于标准化后的三维矩阵,计算相应的正交矩阵、得分矩阵、负载矩阵和、其残差矩阵和组合得分矩阵,PARAFAC2模型定义如下

①SPE特征证据源:对于离线过程,第批次,采样时刻的SPE值为
(12)
在线过程采样时刻的SPE值为
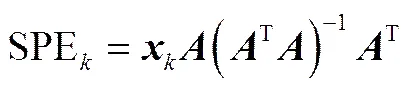
②2特征证据源:对于离线过程,对于第批次,且采样时刻的2值为
(14)
其中,为所有(=1,…,)的协方差矩阵
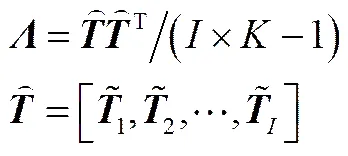
在线过程采样时刻的2值为
(16)
根据式(12)和式(14)计算出离线情况下建模数据的SPE和2,使用核密度估计[27](kernel density estimate,KDE)方法计算不同显著水平时的SPE和2的控制限用于在线监测。
(3)多证据源的BPA输出
历史数据集经过数据预处理后,作为MPCA和PARAFAC2统计模型的输入,输出的是相应统计量的控制限。传统异常检测方法中,通过计算在线时刻数据的统计量,并与统计量相应的控制限作比对,若超过控制限,则判定时刻的数据存在异常;反之,则数据正常。此方法无法实现BPA分配。
传统的统计模型设定历史过程测量数据集服从特定分布和显著性水平,属于该数据集的置信度为1-,能够计算出在该显著性水平下的异常判定控制限。因此,本文为统计模型设计一种BPA计算方法,设当前的统计模型为,统计量为和显著水平集合为=[0.01,0.02,…,0.99]。首先,在显著水平集合为时计算异常检测控制限Limit();然后,在线计算时刻数据样本的统计量为f;最后,搜寻Limit(down)<f< Limit(up)区间,寻找将该点判为异常的最大概率down,进而设置down作为模型和统计量在时刻的证据源异常BPA输出。
2.3 多证据融合的决策方法
获得各证据的BPA,经证据理论融合处理,得到识别框架中所有可能发生状态命题的总信度值,由以下规则确定检测结果[28]。
(1)(F)max{(F)},目标命题具有最大的BPA。
(2)(F)m(F)1,且(F)m()0,目标命题的BPA与其他命题的BPA差值必须大于某一阈值,且目标的BPA必须大于不确定区间的长度。
(3)()2,即不确定度必须小于某一阈值。
其中,F为决策结构,1值设为0.2,2值设为0.1。规则(1)是间歇过程数据异常检测的基本条件,规则(2)确保检测结果的BPA占有较大优势,规则(3)确保样本是充分可判的。如以上3个规则不能同时满足,则无法获得结论,则输出决策结果为不确定。通过以上多证据融合决策方法实现对间歇过程数据异常检测决策判断。
3 实验与分析
3.1 实验数据
青霉素是一种具有广泛临床医用价值的抗生素,其生产过程是一个典型的非线性、动态和多时段的间歇生产过程。Pensim仿真平台[29]为青霉素发酵过程测量数据异常检测提供了标准的过程仿真数据。实验过程选取10个主要过程变量,如表1所示。设定不同的初始条件,生成20个正常批次数据,采样时间为400 h,采样间隔为1 h,在每批次数据中加入高斯白噪声。生成5个异常批次,异常批次的情况如表2所示。
3.2 实验结果与分析
根据历史情况统计,间歇过程可能发生的状态为平稳状态、异常状态。构建识别框架={平稳状态,异常状态},()为不确定度。历史数据按照两种数据标准化方法,分别使用MPCA和PARAFAC2多变量统计分析方法,计算SPE和2统计量的证据源。设定保留原有数据空间中85%以上的信息,使用累积贡献率[30]方法计算得到需要保留的主成分个数。对于测试批次,输入多证据融合决策的间歇过程数据异常检测模型,实现在线间歇过程数据异常检测。下列实验结果通过多次实验求得的平均值作为最终实验结果。

表1 青霉素发酵过程变量说明
Note: 1cal=4.1868J.

表2 青霉素发酵过程异常批次说明

表3 不同监测方法的异常检测率
基于批次方向展开标准化的B-MPCA和B-PARAFAC2与基于变量方向展开标准化的V-MPCA和V-PARAFAC2的异常检测率和误检率结果如表3和表4所示。对于不同的异常类型,如:B-MPCA考察的是不同操作批次间的随机波动,通过判断波动大小是否服从多维正态分布,进而判断是否发生故障。在异常批次1中,由专家机理知识可知,异常持续位置正好处于过程过渡阶段,因此,历史训练批次中,时间段的随机波动相对较大,训练而得异常检测模型难以检测较小的异常;而对于其他异常批次,异常持续位置处于过程发展的主要阶段,因此B-MPCA均有较好的异常检测结果。
不同异常检测方法的检测性能均不相同,而且不同统计量对不同异常的敏感程度也不一样。然而,如表4所示,由于V-MPCA方法中的2统计量证据源提供了错误信息,使用传统的D-S证据融合方法虽然能提高数据异常检测精度,但同时也带来了较高的误检率。所提出的改进冲突证据处理方法进行证据融合,能够减少证据冲突导致的错误融合结果,利用权重对证据源预处理,给伪证据较小权重减小了其对融合结果的影响,相比于传统的D-S方法,不仅提高了数据异常检测率,而且降低了数据异常误检率。

表4 不同监测方法的异常误检率
从表3和表4可知,单一特征源进行间歇过程测量数据异常检测,准确率偏低,平均准确率小于30%;多证据融合决策的间歇过程测量数据异常检测平均准确率达到80%。
4 结 论
间歇过程的测量数据具有高维、非线性、非高斯分布特征。将证据融合引入间歇过程测量数据异常检测,融合多源证据信息,能够有效提高间歇过程异常检测准确率;针对证据理论融合中存在的冲突证据,所提出的多证据融合决策的间歇过程测量数据异常检测方法充分利用证据源的冗余互补信息,采用主焦元判别伪证据,并重新计算证据权重,能够有效地处理冲突证据,提高了间歇过程测量数据异常检测的准确性,有较好的泛化能力和稳定性,降低了误检和漏检率。
References
[1] BAKSHI B R, LOCHER G, STEPHANOPOULOS G,. Analysis of operating data for evaluation, diagnosis and control of batch operations[J]. Journal of Process Control, 1994, 4(4): 179-194.
[2] WISE B M, GALLAGHER N B, BUTLER S W,. A comparison of principal component analysis, multiway principal component analysis, trilinear decomposition and parallel factor analysis for fault detection in a semiconductor etch process[J]. Journal of Chemometrics, 1999, 13(3/4): 379-396.
[3] RATO T J, RENDALL R, GOMES V,. A systematic methodology for comparing batch process monitoring methods(Ⅰ): Assessing detection strength[J]. Industrial & Engineering Chemistry Research, 2016, 55: 5342-5358.
[4] CAMACHO J, PICÓ J, FERRER A. Bilinear modelling of batch processes(Ⅰ): Theoretical discussion[J]. Journal of Chemometrics, 2008, 22(5): 299-308.
[5] 曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进[J]. 化工学报, 2013, 64(3): 788-800. CAO P F, LUO X L. Modeling of soft sensor for chemical process[J]. CIESC Journal, 2013, 64(3): 788-800.
[6] WANG H, YAO M. Fault detection of batch processes based on multivariate functional kernel principal component analysis[J]. Chemometrics & Intelligent Laboratory Systems, 2015, 149: 78-89.
[7] 王立敏, 杨继胜, 于晶贤, 等. 基于T-S模糊模型的间歇过程的迭代学习容错控制[J]. 化工学报, 2017, 68(3): 1081-1089. WANG L M, YANG J S, YU J X,. Iterative learning fault-tolerant control for batch processes based on T-S fuzzy model[J]. CIESC Journal, 2017, 68(3): 1081-1089.
[8] KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry[J]. Computers & Chemical Engineering, 2009, 33(4): 795-814.
[9] ZHANG Z J, CHEN J H. Correntropy based data reconciliation and gross error detection and identification for nonlinear dynamic processes[J]. Computers & Chemical Engineering, 2015, 75: 120-134.
[10] CENCIC O, FRÜHWIRTH R. A general framework for data reconciliation(Ⅰ): Linear constraints[J]. Computers & Chemical Engineering, 2015, 75: 196-208.
[11] 蒋余厂, 刘爱伦. 基于GLR-NT的显著性误差检测与数据协调[J]. 华东理工大学学报(自然科学版), 2011, 37(4): 502-508. JIANG Y C, LIU A L. Gross error detection and data reconciliation based on a GLR-NT combined method[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2011, 37(4): 502-508.
[12] GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562.
[13] WANG J S, CHIANG J C. A cluster validity measure with outlier detection for support vector clustering[J]. IEEE Transactions on Systems Man and Cybernetics, Part B-Cybernetics, 2008, 38(1): 78-89.
[14] 田慧欣, 毛志忠, 赵珍. 与软测量建模相结合的过失误差侦破新方法[J]. 仪器仪表学报, 2008, 29(12): 2658-2662. TIAN H X, MAO Z Z, ZHAO Z. New method of gross error detection combined with soft sensor modeling[J]. Chinese Journal of Scientific Instrument, 2008, 29(12): 2658-2662.
[15] COAKLEY D, RAFTERY P, KEANE M. A review of methods to match building energy simulation models to measured data[J]. Renewable and Sustainable Energy Reviews, 2014, 37(3): 123-141.
[16] NARASIMHAN S, BHATT N. Deconstructing principal component analysis using a data reconciliation perspective[J]. Computers & Chemical Engineering, 2015, 77: 74-84.
[17] LUO L J, BAO S Y, MAO J F,. Phase partition and phase-based process monitoring methods for multiphase batch processes with uneven durations[J]. Industrial & Engineering Chemistry Research, 2016, 55(7): 2035-2048.
[18] ZADEH L A. A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination[J]. AI Magazine, 1986, 7(2): 85-90.
[19] 陈斌, 万江文, 吴银锋, 等. 神经网络和证据理论融合的管道泄漏诊断方法[J]. 北京邮电大学学报, 2009, 32(1): 5-9. CHEN B, WAN J W, WU Y F,. A pipeline leakage diagnosis for fusing neural network and evidence theory[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(1): 5-9.
[20] GHOSH K, NATARAJAN S, SRINIVASAN R. Hierarchically distributed fault detection and identification through Dempster-Shafer evidence fusion[J]. Industrial & Engineering Chemistry Research, 2011, 50(15): 9249-9269.
[21] HUI K H, LIM M H, LEONG M S,. Dempster-Shafer evidence theory for multi-bearing faults diagnosis[J]. Engineering Applications of Artificial Intelligence, 2017, 57: 160-170.
[22] DEMPSTER A P. The Dempster-Shafer calculus for statisticians[J]. International Journal of Approximate Reasoning, 2008, 48(2): 365-377.
[23] LIU W R. Analyzing the degree of conflict among belief functions[J]. Artificial Intelligence, 2006, 170(11): 909-924.
[24] MURPHY C K. Combining belief functions when evidence conflicts[J]. Decision Support Systems, 2000, 29(1): 1-9.
[25] NOMIKOS P, MACGREGOR J F. Monitoring batch processes using multiway principal component analysis[J]. AIChE Journal, 1994, 40(8): 1361-1375.
[26] KIERS H A L, TEN BERGE J M F, BRO R. PARAFAC2(Ⅰ): A direct fitting algorithm for the PARAFAC2 model[J]. Journal of Chemometrics, 1999, 13(3/4): 275-294.
[27] 韩敏, 张占奎. 基于改进核主成分分析的故障检测与诊断方法[J]. 化工学报, 2015, 66(6): 2139-2149. HAN M, ZHANG Z K. Fault detection and diagnosis method based on modified kernel principal component analysis[J]. CIESC Journal, 2015, 66(6): 2139-2149.
[28] BASIR O, YUAN X H. Engine fault diagnosis based on multi-sensor information fusion using Dempster-Shafer evidence theory[J]. Information Fusion, 2007, 8(4): 379-386.
[29] BIROL G, ÜNDEY C, CINAR A. A modular simulation package for fed-batch fermentation: penicillin production[J]. Computers & Chemical Engineering, 2002, 26(11): 1553-1565.
[30] JACKSON J E. A User's Guide to Principal Components[M]. New York: John Wiley & Sons, 2005.
Multi-evidence fusion decision-making method for detecting abnormal data of batch processes
LIU Weimin, WANG Jianlin, QIU Kepeng, YU Tao, ZHAO Liqiang
(College of Information Science and Technology, Beijing University of Chemical Technology, Beijing100029, China)
High-dimensional, non-linear, and non-Gaussian distributions of measured data in batch processes directly influence accuracy of detecting abnormal data. In order to integrate information of multi-source abnormal detection and increase detection accuracy, a method was proposed on the basis of multi-evidence fusion decision. With introduction of the Dempster-Shafer evidence theory, the main focal element was used to identify fake evidence and to recompute weight of evidences. The re-calculation on weight of evidences improved handling conflict evidences, reduced influence of conflict evidences on multi-evidence fusion decision, and enhanced detection accuracy of abnormal measured data. Furthermore, an abnormal detection model was constructed from multi-evidence fusion decision and was applied to decision-making of abnormal data detection in batch processes. The experimental results show that the proposed method can combine multi-evidence information and analyze conflict evidence effectively. Thus abnormal data detection for batch processes is achieved with low false and missing detection rates.
batch processes; Dempster-Shafer theory; conflicting evidence; multi-evidence decision; abnormal measured data detection
10.11949/j.issn.0438-1157.20170117
TQ 277
A
0438—1157(2017)08—3183—07
王建林。第一作者:刘伟旻(1989—),男,博士研究生。
国家自然科学基金项目(61240047);北京市自然科学基金项目(4152041)。
2017-02-26收到初稿,2017-04-22收到修改稿。
2017-02-26.
Prof. WANG Jianlin, wangjl@ mail.buct.edu.cn
supported by the National Natural Science Foundation of China (61240047) and the Natural Science Foundation of Beijing (4152041).
