超声传输时间法颈动脉脉搏波速估计精度及影响因素研究

2017-10-13张榆锋杨丽春李支尧张俊华

电子与信息学报 2017年2期

邓丽张榆锋杨丽春胡晓李支尧高莲张俊华

邓丽①张榆锋*①杨丽春②胡晓①李支尧②高莲①张俊华①

①(云南大学信息学院昆明 650091)②(昆明医科大学第三附属医院昆明 650031)

该文基于传播模型定量分析了超声传输时间法检测局部脉搏波速(PWV)过程中扫描帧频与声束数对脉动位移曲线估计、延迟时间估计及PWV拟合的估计精度，采用方差分析确定了误差显著性和影响因素的主次关系。结果表明，脉动位移相对误差在0.23~0.28之间，帧频对其估计精度影响不显著()；延迟时间估计同时受声束对距离和帧频的影响()，声束对间距从2.38 mm增大到 38 mm，平均相对误差由0.99减至0.06；帧频从1127 Hz 减小为226 Hz，平均相对误差由0.19 增至 0.43; PWV拟合受声束数及帧频的共同影响，声束数不小于10时，估计误差为7%~20%，帧频为主要影响因素()。因此，在保证合理声束数条件下，提高帧频可改善PWV的估计精度。结果有助于为后续PWV检测精度的改进研究提供依据。

超声射频信号；颈动脉；脉搏波速；精度性能

1 引言

动脉硬化、原发性高血压患者与心血管病死亡率有重要关系，对预防和早期诊断心血管疾病有重要意义[1]。定量描述主动脉管壁弹性程度的参数包括血管脉动扩张度、顺应性系数、杨氏弹性模量及脉搏波传播速度(Pulse Wave Velocity, PWV)等。其中，PWV直接与动脉杨氏弹性模量有关，是动脉硬化定量评价的优选方法[2]。同一段血管不同局部弹性存在明显差异，近年来，局部PWV检测已成为定量评价动脉硬化的研究热点[3]。

超声技术因其操作简单，无创，实时性等优点，已成为目前动脉局部PWV检测的主要手段[4]。具体包括传输时间(Transit Time, TT)法[5]、血流面积法[6]、相位法[7]、管径梯度法[8]等。其中，TT法通过检测动脉血管上一段特定距离内脉搏波传输延迟时间，并根据距离时间比计算该段血管上脉搏波平均速度。因无需测量血管直径、管壁厚度、局部弹性模量等参数，该方法在超声颈动脉局部PWV的临床检测研究中被广泛使用。Hasegawa等人[9]使用超声平面波扫描提高帧频和声束密度，临床采集3例正常人体颈动脉B超序列图像及对应的射频信号，基于TT法得到的PWV值范围在5.6~7.0 m/s之间。Sorensen等人[10]利用超声扫描仪(RASMUS)采集1例36岁正常男性的颈动脉B超序列图像，在已知距离内利用互相关估计管壁径向脉动位移(Distension Wave Form, DWF)，然后比较了两种DWF互相关延迟时间估算方案获取PWV的结果。其中，方案1用第个声束位置与第个对应的DWF进行互相关；方案2利用第个声束位置与第个对应的DWF进行互相关。结果表明，方案2获得的PWV值在4~9 m/s之间，与方案1相比其结果更接近文献报道。Luo等人[11]使用彩色超声诊断系统，通过将帧频从140 Hz增至1127 Hz，每帧扫描声束减至16线的方法临床采集正常人体一段颈总动脉的B超序列图像，利用射频信号进行互相关提取不同位置管壁脉动曲线，并对该结果再次互相关估算脉搏波传播延迟时间，最后对序列延迟时间进行线性拟合估算PWV。研究表明，该方法估计的正常人体颈动脉局部PWV值范围在4.0~ 5.2 m/s。对比分析上述研究方案及实验结果发现，基于超声射频信号的TT法需要综合设定超声扫描帧频与每帧扫描声束数(声束密度)，信号的处理涉及脉动位移曲线估计、延迟时间估计及PWV拟合3个步骤。检测参数及处理环节相互影响，造成这些研究中获得的人体正常颈动脉局部PWV值的范围存在较大差异。而直接针对临床采集信号进行分析处理的试验方法无法对检测的准确性及其估计过程中相关因素的影响进行系统研究。

为此，本文基于临床提取的脉动位移曲线提出了PWV为4.5 m/s的颈动脉脉搏波传播超声仿真模型，定量比较分析了射频超声TT法PWV检测过程中不同扫描帧频与声束数下，脉动位移曲线估计、延迟时间估计及PWV拟合产生的误差，系统研究了扫描帧频、声束数对颈动脉PWV检测精度影响的显著性。首先构建了颈动脉脉搏波局部传播超声仿真模型，在长度为38 mm血管段产生帧扫描线为16，帧频分别为1127 Hz, 564 Hz, 376 Hz, 226 Hz的30组射频回波信号；利用归一化互相关法对信号进行运动追踪处理，分别获取4种帧频条件下3个处理环节估计值，即：一个心动周期内各声束位置对应的脉动位移曲线、脉搏波从第1线声束位置传输到其余各声束位置的延迟时间以及声束数分别为2至15拟合获得的PWV估计值；然后对比分析了3个处理环节估计值与模型预设值的相对均方根误差；最后通过方差分析法确定帧频与声束数对这3个处理环节估计精度影响的显著性及主次关系。研究结果有助于把握TT法检测局域PWV的精度及其误差产生的原因，对后续改善PWV估计处理方法，提高PWV检测精度具有重要意义。

2 方法原理

2.1 超声TT法颈动脉PWV检测原理

超声TT法检测动脉局域PWV的原理：利用线阵超声探头以16线声束沿脉搏波传播方向从左到右对一段颈总动脉血管进行扫描。PWV检测过程包括：(1)移动互相关估计16个声束位置的脉动位移曲线；(2)移动互相关估计声束1与其余15个声束位置两点间的脉搏波传输时间，计算两点间的PWV值；(3)对整段血管两两点估计的结果线性拟合获得PWV的平均值。利用移动互相关检测脉动位移或脉搏波传播时间的方法中，令为最大相关系数，其定义式可表示为[12]

2.2 颈动脉脉搏波传播超声仿真模型

为了系统研究扫描帧频与声束数对TT法估计PWV所涉及3个处理环节精度的影响，建立逼真的颈动脉脉搏波传播超声仿真模型是关键。本文通过临床采集正常人10个心动周期内颈动脉血管超声射频信号，经移动互相关处理获得脉动位移曲线，然后按4.5 m/s的脉搏波传播速度对齐前向波构建脉搏波传播模型，进而使用Field II仿真超声扫描射频回波信号[13]。

2.2.1 颈动脉血管的几何模型及组织散射模型长38 mm、宽8.5 mm及高25 mm的立方体中央，水平放置直径分别为6 mm和8.5 mm的同心嵌套圆柱体，构成了长度为38 mm，管腔直径为6 mm，管壁厚度为1.25 mm的颈动脉血管几何模型。组织散射模型由血管壁、血管外周组织及血流3部分组成，共包含个散射点(密度为,为超声波长)，其位置服从均匀分布，幅度服从瑞丽分布[14]。

2.2.2 脉搏波传播超声仿真为了获得逼真的颈动脉脉搏波传播模型，本文首先通过临床采集正常人颈动脉脉动超声回波射频信号。使用SonixTouch RP超声系统及线阵探头L14-5w/60(Ultrasonix RP, 加拿大优胜医疗有限公司)采集正常人10个心动周期的颈动脉血管超声射频信号，帧频为1127 Hz，扫描声束为16线，探头中心频率为10 MHz，扇区宽度为38 mm。然后使用TT法提取每线声束位置处10个心动周期的脉动位移曲线，并作集合平均降噪处理后获得一个心动周期的脉动位移曲线，最后进行延迟时间估计，线性拟合处理计算PWV值。图1为一个心动周期内16线声束位置对应的血管壁脉动位移曲线及在0至0.6 s内相应的时间-声束位置脉动速度分布图，其中，图1(a)所示为集合平均后的临床脉动位移曲线，可看出各声束位置对应的脉动位移曲线具有大致相同的变化规律，由近及远逐渐产生延迟。图1(b)为2维灰度图表示的管壁脉动速度随时间和空间位置变化分布(即对图1(a)脉动位移求导结果)，圆圈标注了16线声束对应的前向速度波峰点，直线代表16个波峰点延迟时间线性拟合结果(其斜率为PWV估计值)；圆圈偏离直线越远说明受斑点噪声的影响，延迟时间出现较大误差。为了建立颈动脉血管壁脉动的动态传输过程模型，本文预设正常人体颈动脉PWV为4.5 m/s，假定血管长度为38 mm，由此计算出16线声束位置对应的脉搏波延迟时间，据此调整对齐临床提取的16个脉动位移曲线(图1(a))前向波峰相对位置，如图1(c)所示。图1(d)为对应的管壁脉动速度分布，图中直线斜率为4.5 m/s的PWV预设值。可以看出，圆圈圆心正好穿过直线，表明脉博波沿血管的传播速度达到预设的4.5 m/s。据此，获得了脉搏波传输过程中不同时刻和声束位置的脉动位移、延迟时间及PWV的模型预设值。为了仿真一个心动周期(1 s)内脉搏波动态传输的超声扫描信号，根据图1(c)中各扫描帧(时间)时，16线声束(位置)处脉动位移量，调整模型中管壁组织散射点的位移，生成颈动脉散射体动态组织模型，产生射频回波信号。

2.3 PWV估计过程中误差统计分析

为了定量对比分析检测参数对各处理环节估计精度的影响，实验中首先计算了各个环节估计量与模型预设值之间的相对均方根误差(Relative Root Mean Squared Error, RRMSE)。具体方法是在4种扫描帧频(1127 Hz, 564 Hz, 376 Hz和226 Hz)条件下，基于30组超声射频信号分别估计16线声束位置处脉动位移、延迟时间以及不同声束数的PWV拟合值，并计算与预设值间的相对均方根误差[15,16]，最后采用双因素方差分析法，将样本总方差来源分为随机误差，因素(帧频)、因素(声束对)及其交互作用引入误差4部分，对各部分误差构造统计量，根据界值表，选用显著性水平为0.05或0.01与显著性值进行比较判断各个因素影响的显著性以及其主次关系[17]。

3 实验与结果

3.1 信号仿真及PWV估计

图2(a)给出了声束为16线、帧频为1127 Hz的仿真条件下获得的脉搏波速度变化的灰度分布图，图2(b)为图2(a)中前向波峰延迟时间线性拟合结果。从图2(a)中圆圈相对位置可看出脉动位移由近及远产生延迟，与图1(c)模型中脉动位移的传播规律一致。此外，前向波和反射波的分布及变化与图1(b)临床变化规律一致。图2(b)中拟合直线斜率的倒数便是PWV估计值(即4.24 m/s)，拟合相关系数达0.97。利用该模型随机仿真了30组超声射频信号，估计的平均延迟时间与预设值相比相对误差为6.2%, PWV平均相对误差为7.0%；进一步提高至60组，延迟时间平均相对误差降为2.8%, PWV平均相对误差降为3.2%。因此，仿真模型不仅反映了临床实际的变化规律和特征，估计过程中的延迟时间和PWV结果也与模型预设值一致，从而验证了本文所提模型的有效性。

3.2 PWV估计各环节误差及影响因素显著性分析

3.2.1 脉动位移及其延迟时间估计误差分析 PWV估计涉及了脉动位移估计、延迟时间估计及PWV线性拟合3个环节。4种不同帧频对应的16个声束位置处脉动位移平均相对均方误差范围在0.23至0.28之间，误差统计分析表明帧频对脉动位移的检测精度影响不显著()，与文献报道的结果一致[18]。

图3(a)为4种不同帧频下，声束1到其余15个声束位置间的脉搏波延迟时间平均相对均方根误差及标准差。从图3(a)中可看出，随着声束对间距增大，延迟时间相对误差整体呈减小趋势，声束对间距从2 增大到 16 , 延迟时间平均相对误差由0.99减至0.06；而帧频从1127 Hz减至226 Hz，延迟时间平均相对误差从0.19 增至 0.43，表明远距声束对与高帧频都能减小延迟时间的估计误差。表1进一步给出了对脉搏波延迟时间进行的双因素方差分析结果。可以看出，帧频、声束对以及二者交互作用对应的显著性均为“* *”，即影响十分显著。这是由于延迟时间估计的本质是通过帧频对时间进行量化来实现，即利用移动互相关法对脉动位移进行运动追踪，所确定的脉搏波移动的时间是以帧频倒数的整数倍来表示。随着帧频减小，声束对之间的延迟时间分辨率也下降，导致误差增大。这也是远距声束对之间延迟时间误差较小的原因。

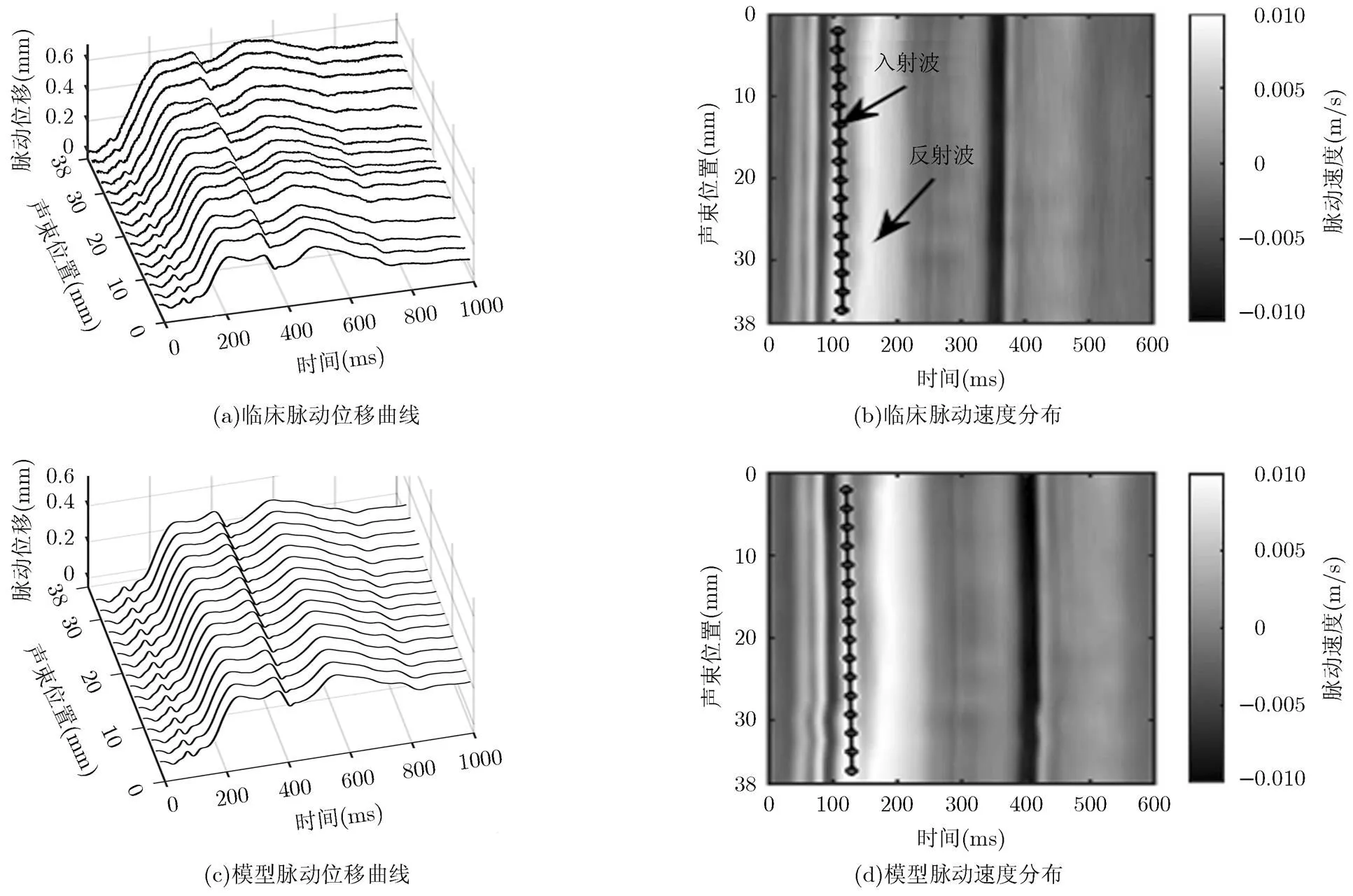
图1 16线声束位置的血管壁脉动位移曲线及其对应的速度分布

图2 16线声束位置的仿真血管壁脉动速度分布及其对应的延迟时间线性拟合结果

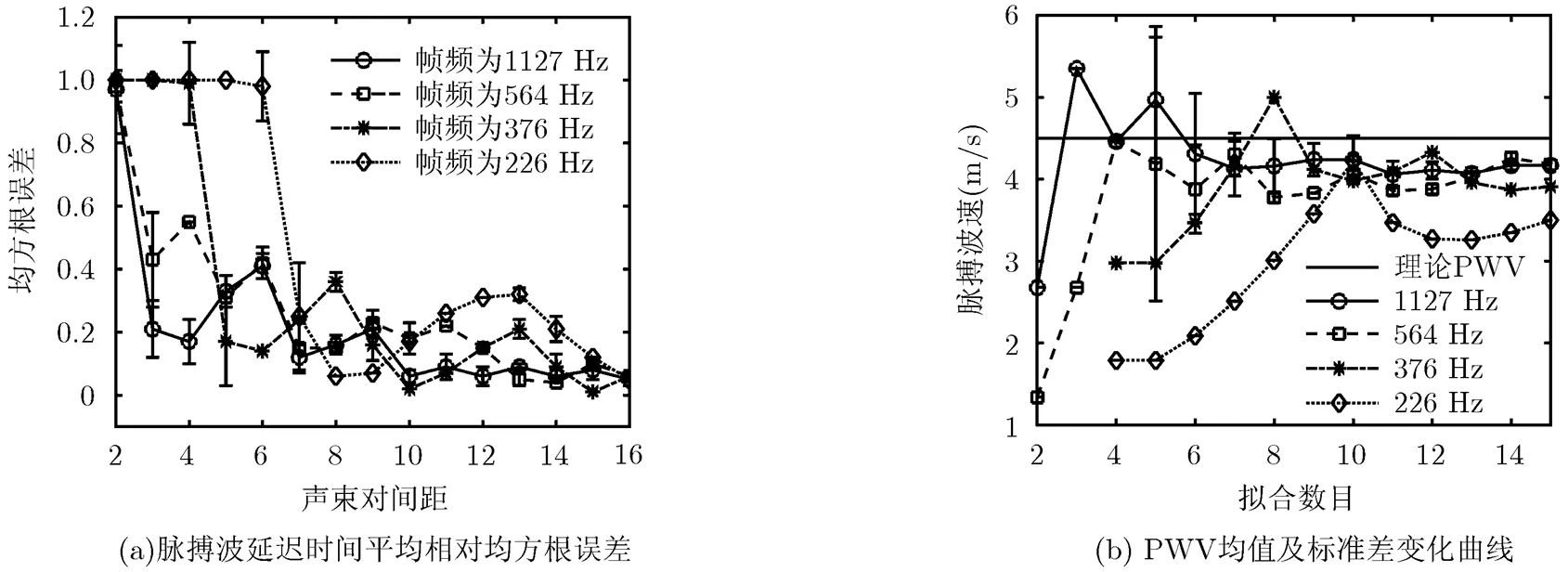
图3 脉搏波延迟时间的平均相对均方根误差曲线以及PWV的标准差变化曲线

表1 对脉搏波延迟时间估计精度进行帧频和声束对的双因素方差分析结果

注：* * 表示影响十分显著

3.2.2 PWV拟合精度分析从图3(b)中可看出，帧频为1127 Hz和564 Hz，拟合点数从5到15时PWV曲线上对应的标准差逐渐减小，而帧频为376 Hz和226 Hz时PWV曲线上标准差均为零，这是因为高帧频提高了脉搏波延迟时间估计的分辨率，量化误差减小，对信号进行移动互相关处理时受随机分布的斑点噪声影响增大。此时尽管精度较高，离散度也加大。反之，较小的帧频降低了脉搏波延迟时间估计的分辨率，升高了量化系统误差，使估计结果受随机斑点噪声的影响也减小。此时，估计精度降低，离散程度也随之减低。进一步定量分析表明，在扫描帧频和声束数的共同影响下，PWV拟合结果在7%~65%范围内存在不同程度误差，而使用10~15个声束数估计的PWV误差为7%~20%，说明拟合处理中声束对个数不宜小于10。

为了确定帧频与声束数对PWV拟合精度的影响显著性以及区分二者影响的主次关系，实验将PWV拟合分为声束数为2~9与声束数为10~15两个水平，并分别对其进行双因素方差分析，其结果如表2所示。由表可知，声束数为2~9时，帧频、声束数以及二者共同作用均对PWV拟合精度的影响十分显著；声束数为10~15时，声束数对PWV拟合精度影响不显著()，而帧频以及帧频与声束数共同作用时对PWV拟合精度均有十分显著的影响()。综上所述，过低的声束密度会导致PWV拟合误差显著增大；在声束数不小于10的情况下，帧频是主要影响因素，此时提高帧频有助于改善PWV拟合精度。

4 结束语

研究结果表明，脉动位移相对误差在0.23~ 0.28之间，帧频对脉动位移估计精度影响不显著()(在此环节，声束相互之间对估计结果没有影响)；随着帧频由1127 Hz 减小到 226 Hz，延迟时间平均相对误差由0.19 增至0.43，远距声束对间延迟时间误差小于近距声束对的，这是由于延迟时间估计是时间量化过程，其精度受帧频和声束对的影响均十分显著()，导致高帧频、远距声束对时延迟时间估计精度较高；PWV拟合在不同声束密度时影响程度不一，声束数小于10时，帧频与声束数对其估计精度影响均十分显著；声束数大于10时，估计误差为7%~20%，精度较高。此时，帧频为主要影响因素()，而声束数影响不明显()。综上所述，在延迟时间估计及PWV拟合过程中保证合理声束配置，侧重于研究信号插值算法或超声平面波扫描技术提高帧频，有望改善PWV估计精度。研究结果不仅有助于把握超声射频信号TT法局域PWV检测精度及其误差产生的原因，而且能够为后续提高PWV检测精度的改进方法研究提供可靠依据。

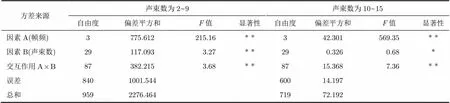
表2 对PWV拟合精度进行帧频和声束数的双因素方差分析结果

注：* * 表示影响十分显著，* 表示影响不显著

[1] GULAN U, LUTHI B, HOLZNER M,. Experimental investigation of the influence of the aortic stiffness on hemodynamics in the ascending aorta[J]., 2014, 18(6): 1775-1780. doi: 10.1007/s00348-012-1371-8.

[2] PETER L, FOLTYN J, and CERNY M. Pulse wave velocity measurement; developing process of new measuring device[C]. Machine Intelligence and Informatics (SAMI) 2015 IEEE 13th International Symposium, Herl’any, Slovakia, 2015: 59-62. doi: 10.1109/SAMI.2015.7061846.

[3] LAURENT S, COCKCROFT J, and BORTEL L V. Expert consensus document on arterial stiffness; methodological issues and clinical applications[J]., 2006, 27(21): 2588-2605.doi: 10.1093/eurheartj/ehl254.

[4] NAGAOKA R, MASUNO G, KOBAYASHI K,. Measurement of regional pulse-wave velocity using spatial compound imaging of the common carotid artery in vivo[J]., 2015, 55(1): 92-103. doi: 10.1016/j.ultras.2014. 07.018.

[5] PILT K, KOOTS K, MEIGAS K,. The aortic pulse wave velocity estimation for arterial stiffness assessment[J]., 2015, 45: 294-297. doi: 10.1007/978- 3-319-11128-5_73.

[6] RABBEN S I, STERGIOPULOS N, and HELLEVIK L R. An ultrasound-based method for determining pulse wave velocity in superficial arteries[J]., 2004, 37(10): 1615-1622. doi: 10.1016/j.jbiomech.2003.12. 031.

[7] KANAI H, SATO M, KOIWA Y,. Transcutaneous measurement and spectrum analysis of heart wall vibrations[J].,, 1996, 43(5): 791-810. doi: 10.1109/58.535480.

[8] BRANDS J P, WILLIGERS M J, LEDOUX A L,. A noninvasive method to estimate pulse wave velocity in arteries locally by means of ultrasound[J]., 1998, 24(9): 1325-1335. doi: 10.1016/ S0301-5629(98)00126-4.

[9] HASEGAWA H, HONGO K, and KANAI H. Measurement of regional pulse wave velocity using very high frame rate ultrasound[J]., 2012, 40(2): 91-98. doi: 10.1007/s10396-012-0400-9.

[10] SORENSEN L G, JENSEN B J, UDESEN J,. Pulse wave velocity in the carotid artery[C].Proceedings of the IEEE International Ultrasonics Symposium, Beijing, China, 2008: 1386-1389. doi: 10.1109/ULTSYM.2008.0336.

[11] LUO J W, LI R X, and KONOFAGOU E E. Pulse wave imaging of the human carotid artery: an in vivo feasibility study[J].,, 2012, 59(1): 174-181. doi: 10.1109 /TUFFC.2012.2170.

[12] LUO J and KONOFAGOU E E. A fast normalized cross-correlation calculation method for motion estimation[J].,, 2010, 57(6): 1347-1357. doi: 10.1109/ TUFFC.2010.1554.

[13] JENSE J A. Speed-accuracy trade-offs in computing spatial impulse responses for simulating medical ultrasound imaging[J]., 2001, 9(3): 731-744. doi: 10.1142/S0218396X01001248.

[14] BALOCCO S and BASSET O. 3D dynamic model of healthy and pathologic healthy and pathologic arteries for ultrasound technique evaluation[J]., 2008, 35(12): 5440-5449. doi: 10.1118/ 1.3006948.

[15] 蔡轶珩, 张琳琳, 盛楠, 等. 基于光度立体法的中医舌体三维表面重建[J]. 电子与信息学报, 2015, 37(11): 2564-2570. doi: 10.11999/JEIT150124.

CAI Yiheng, ZHANG Linlin, SHENG Nan,. 3D reconstruction of tongue surface based on photometric stereo method[J].&, 2015, 37(11): 2564-2570. doi: 10.11999/JEIT150124.

[16] GAO L, ZHANG Y F, and LIN W J. A novel quadrature clutter rejection approach based on the multivariate empirical mode decomposition for bidirectional Doppler ultrasound signals[J]., 2014, 13(13): 31-40. doi: 10.1016/j.bspc.2014.03.003.

[17] 魏子翔, 崔嵬, 李霖, 等. 一种基于最大似然估计的合作目标多维参数跟踪算法[J]. 电子与信息学报, 2015, 37(6): 1450-1456. doi: 10.11999/JEIT141150.

WEI Zixiang, CUI Wei, LI Lin,. Maximum likelihood estimation based algorithm for tracking cooperative target[J].&, 2015, 37(6): 1450-1456. doi: 10.11999/JEIT141150.

[18] STADLER R, TAYLOR A, and LEES R. Comparison of B-mode, M-mode and echo-tracking methods for measurement of the arterial distension waveform[J]., 1997, 23(6): 879-887. doi: 10.1016/S0301-5629(97)00074-4.

Accurate Performance and Associated Influence Factors for Pulse Wave Velocity Measurement of Carotid Arteries Based on Ultrasonic Transit Time Method

DENG Li①ZHANG Yufeng①YANG Lichun②HU Xiao①LI Zhiyao②GAO Lian①ZHANG Junhua①

①(,,650091,)②(,650031,)

The estimation accuracy of the wall displacement, delay time, and linear-regression-based Pulse Wave Velocity (PWV) affected by different scanning frame rates and beam density is investigated quantitatively in the measurement of the regional PWV with ultrasound transit time method based on a model of pulse wave propagation along a carotid artery segment. Through statistical variance analysis, the significance levels of measurement errors as well as the primary and secondary relations of these two influence factors are ascertained. The results show that the frame rates do not significantly affect the wall displacement estimation accuracy () with relative errors ranged from 0.23 to 0.28. The delay time measurement accuracy is influenced significantly by the frame rates and spacing between two beams simultaneously (). The relative errors decrease from 0.99 to 0.06 as the distances from the first beam to others increase from 2.38 mm to 38 mm. However, the mean transit time errors increase from 0.19 to 0.43 when the frame rates decrease from 1127 Hz to 226 Hz. The PWV estimation errors ranging from 7% to 20% are affected significantly by the number of beams as well as frame rates under the condition that the beams used for regression fitness are no less than 10. The frame rate is the main influence factor in this situation (). Therefore, the PWV measurement accuracy can be improved by increasing frame rate with a proper beam setting. Experimental results could be helpful to explore novel measurement method for improving PWV accuracy in the follow-up work.

Ultrasound radio frequency signal; Carotid artery; Pulse wave velocity; Accurate performance

R445.1

1009-5896(2017)02-0316-06

10.11999/JEIT160306

2016-03-31；改回日期：2016-09-09；

2016-11-14

张榆锋 yfengzhang@yahoo.com

国家自然科学基金(61261007, 61561049)，云南省自然科学基金(2013FA008)

The National Natural Science Foundation of China (61261007, 61561049 ), The Natural Science Foundation of Yunnan Province (2013FA008)

邓丽：女，1991年生，博士生，研究方向为超声医学信息处理.

张榆锋：男，1965年生，教授，博士生导师，现主要从事微弱信号检测、超声医学工程等.

杨丽春：女，1960年生，教授，主要研究方向为超声医学、超声诊断及介入超声.