基于改进BRISK的图像拼接算法

董 强 刘晶红 王 超 周前飞



基于改进BRISK的图像拼接算法

董 强①②刘晶红*①王 超③周前飞①②

①(中国科学院长春光学精密机械与物理研究所 长春 130033)②(中国科学院大学 北京 100049)③(解放军77110部队 什邡 618400)

为了获得精准的航空拼接图像，更好地解决图像拼接中经常出现的尺度变化、角度旋转、光照差异以及传统的BRISK(Binary Robust Invariant Scalable Keypoints)算法匹配正确率较低，图像拼接精度低等问题，该文提出一种全新的基于有向线段的BRISK特征的图像拼接模型。首先，使用BRISK算法进行图像匹配，得到粗匹配点对，再构造有向线段及其BRISK特征进行邻近线段匹配，通过概率统计模型进行特征点的精匹配，最后进行加权融合和亮度均衡化进行图像融合完成图像拼接。实验结果表明，该文算法针对图像的光照条件不同、角度旋转、分辨率低、尺度变化等均有良好的鲁棒性和稳定性，该文算法是一种耗时短、精确度高、拼接效果良好的图像拼接方法。

图像配准；图像拼接；BRISK特征；邻近线段

1 引言

近年来，随着计算机技术的飞速发展，图像处理技术也得到空前的提升，作为其重要组成部分的图像拼接已经广泛应用于图像压缩、虚拟现实、医学图像处理等各领域。图像拼接主要分为图像预处理、图像配准和图像融合3个步骤。

图像配准技术是图像拼接的关键。其方法大体分为两类：基于灰度信息的配准方法和基于特征的配准方法。基于灰度的图像配准方法较为简单，直接计算图像间的灰度值关系来匹配图像，这种方法虽然简单、易实现，但其稳定性差，对光照变化敏感。相比之下，基于局部特征的方法具有良好的稳定性，在克服图像的光照、尺度、旋转等变化上比基于灰度的方法有更好的鲁棒性，是目前主流的图像配准方法。

SIFT(Scale Invariant Feature Transform)特征检测算法是Lowe于1999年提出并在2004年完善的，该算法对于尺度缩放、平移旋转、光照变化都具有良好的不变性，对于图像的仿射变换及噪声也具有一定的稳定性，但其描述算子复杂，运行时间过长，很难满足实时性要求。针对SIFT算法在低分辨率图像中出现的误匹配点对较多的问题，文献[12,13]引入一种有向线段匹配方法，能够有效的提高SIFT的匹配正确率，但其增加了算法的复杂度，运行时间较SIFT算法更长。BRISK(Binary Robust Invariant Scalable Keypoints)算法解决了SIFT算法在实时性方面的不足，极大的提高了匹配速度，但相较于SIFT算法，该算法的鲁棒性明显降低，误匹配率较高[14,15]。

兼顾配准精度及运行时间，本文引入一种有向线段BRISK特征的图像配准算法。该算法通过构造有向线段BRISK特征的方法，充分利用图像细节信息，对匹配点进行精确定位，能够有效剔除误匹配点，提高配准的准确率和精度，同时，由于BRISK特征的提取匹配时间较短，本文增加的时间开销很少。实验表明本文算法匹配准确率高于SIFT算法和BRISK算法，运行时间远远小于SIFT算法，经过本文算法获得的遥感拼接图像无明显错位，拼接精度高。

2 BRISK算法

BRISK 算法主要包含3步：角点检测、特征描述、特征匹配。首先，构建尺度空间金字塔，并通过AGAST(Adaptiveand Generic Accelerated Segment Test)角点检测算子提取连续尺度空间中亚像素级精度的稳定极值点。然后，利用局部图像邻域内随机采样点对的灰度大小关系来建立局部图像的二值特征描述子。最后，采用汉明距离进行特征匹配。

3 改进BRISK算法

本文针对BRISK存在的问题，对BRISK的匹配算法提出改进，首先采用BRISK算法进行基于特征的图像匹配，在寻找到匹配点对后，利用匹配点建立有向线段和线段特征进行邻近线段匹配，采用概率统计方法精确寻找正确的匹配点对，提高匹配精度，增强算法的鲁棒性和稳定性。

3.1 构造线段特征

3.2 邻近线段匹配

本文构造一种邻近线段匹配模型，假定在参考图像和待配准图像中构造了条有向线段，表示为和。记：有向线段的特征描述为，有向线段的特征描述为。

因为本文采用矩阵作为有向线段的特征描述，故计算矩阵的F-范数进行邻近线段匹配，即：。得到长度为的向量，对进行归一化，当小于给定的阈值时，即为的邻近线段。本文阈值取0.6。

3.3 特征点匹配

利用邻近线段匹配准则得到了有向线段的匹配，为了得到精确的拼接图像，有必要得到更精确的匹配点。对于给定的两幅图像的匹配点和，使用统计模型来获得匹配点的出现频率，从而进行点的匹配。

如果两条有向线段匹配，那么这两条线段的起点和终点是两对匹配点。首先建立统计矩阵,的计算过程如下：

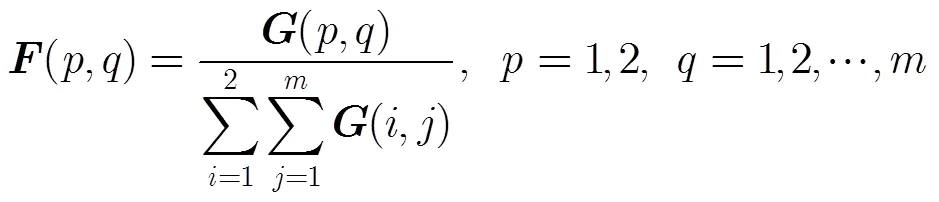
图1 TP值对匹配的影响

利用经典BRISK算法匹配图像后，易产生大量误匹配点对。本文通过构造有向线段的方法，充分利用匹配点间的图像信息，能够有效地剔除误匹配点对。如图2所示，与是参考图像与待配准图像中的3组匹配点对，其中，为一组误匹配点对。分别在两幅图像中利用本文算法构造有向线段,,和。,,分别为有向线段,,的中点，,,分别为有向线段的中点。由图2可以看出与在图像中的位置不同，像素点周围的图像信息差异较大，点在图像中的位置一致，其周围的纹理信息相同。故以两端点及中点的BRISK特征作为有向线段描述进行邻近线段匹配时，和能够有效地进行匹配，,和,由于特征差异较大，不能够进行匹配，从而误匹配点对得以剔除。

图2 误匹配点剔除

4 图像拼接及融合算法

在获得两幅图像的精确匹配特征点对后，由式(4)图像变换关系可以求解出变换矩阵，将待配准图像通过进行变换后与参考图像进行叠加。

由于输出图像存在亮度等方面的差异，在完成图像配准叠加后，在得到的拼接图像上一般会存在明显的缝合线，不利于视觉观察，本文可以采用加权平滑算法来实现两幅图像间的融合过渡[16]。融合方法如下：

式中，1为图像1的非重合区域，3为图像2的非重合区域，2为两幅图像的重叠区域，1和2分别为加权值，与重叠区域有关，并且：,,。在重叠区域，1由1平滑变到0,2由0平滑变到1，这样就实现了两幅图像的融合。

5 实验结果及分析

本文基于改进的BRISK算法图像拼接流程如图3所示。

针对本文提出的改进BRISK算法，采用了大量图像进行实验，并将本文算法与BRISK算法、SIFT算法进行比较，对其匹配性能和拼接精度进行了定量评价与分析。

5.1 运行环境

算法运行环境为：CPU为Intel core i5, 3.20 GHz，内存为4 GB的PC机，32位Win7操作系统，Matlab版本为Matlab 8.1.0.604(R2013a)。

5.2 评价指标

本文采用3个参数对实验结果进行综合评价。

(1)采用运行时间对匹配速度进行评价。

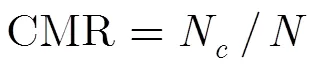
5.3 配准性能评价

图4为实验图像，分别对本文算法的抗光照、抗旋转、分辨率低、及抗尺度变化性能进行测试，并且与BRISK算法和SIFT算法进行对比。图4中各图像对大小为748×534像素、696×524像素、710×536像素、708×410像素。

表1给出使用BRISK算法、SIFT算法和本文算法对上述4组图像进行配准实验的正确匹配点对数、匹配正确率及算法运行时间。表2给出本文算法的各个步骤的耗时。

图3 图像拼接流程图

图4 测试图像

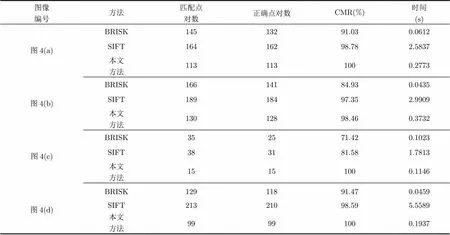
表1 3种方法的匹配结果对比

表2 本文算法时间分析(s)

由表1比较可以看出，本文算法对图像的光照变化、旋转、分辨率低及尺度变化都有较强的鲁棒性和稳定性。相较与BRISK算法，虽然本文算法运行时间略长，但匹配正确率获得极大的提高。相较与SIFT算法，本文算法获取的匹配特征点数略少，但运行时间大大减少，匹配正确率也有所提高。

由表2可以看出，本文算法相较与BRISK算法增加的时间消耗主要集中在有向线段的构造与特征提取部分，且增加的时间与BRISK算法中的匹配点对数有关，增加的时间消耗与匹配点对数成二次方关系，这是因为提取的有向线段数为,为粗匹配点对数。虽然本文算法较BRISK算法用时增加，但精度大大提高，同时算法时间仍远远少于SIFT算法用时。

均衡时间与精度两方面，本文算法较前两种算法更具优越性。

5.4 图像拼接结果

分别不同的图像配准算法对图像进行拼接，放大拼接边缘，拼接结果如图5所示，图5(a)、图5(b)、图5(c)分别为BRISK算法、SIFT算法、本文方法的拼接图像，图5(d)、图5(e)、图5(f)为上述3种方法的拼接边缘放大图像，即图中标注区域。由图5(d)可以看出，BRISK算法拼接图像精度最差，有明显错位，由图5(e)可以看出，SIFT算法拼接图像精度良好，明显错位较少，拼接精度较BRISK算法有很大提高，图5(f)可以看出，本文算法无明显的接缝，拼接精度较前两种算法均有显著提高。

图5 图像拼接比较

最后，针对两图像亮度差异产生的明显接缝，采用如前所述的加权平滑算法对图像进行处理，得到亮度变化均匀，无明显接缝，无鬼影，保真度高的拼接图像，如图6所示。

图6 拼接图像

6 结论

针对基于BRISK的拼接算法误匹配率高、拼接精度低的问题，本文提出一种全新的基于有向线段BRISK特征的图像拼接方法，并与BRISK算法和SIFT算法进行对比。首先利用BRISK算法进行粗匹配，再利用匹配点构造有向线段及其特征，采用邻近线段匹配法及概率统计模型进行特征点的精确匹配，最后利用加权融合算法和亮度均衡化实现图像的融合拼接。实验结果表明，本文算法对于图像拼接中经常出现的光照强度差异、角度旋转、分辨率低及尺度变化等问题都具有较强的鲁棒性和稳定性。相较于BRISK算法，本文算法能够有效地剔除误匹配点，提高匹配正确率，为图像拼接提供更为准确的变换模型，因此，本文算法的拼接精度较BRISK算法更高。相较于SIFT算法，本文算法精度有所提高，但运行时间大大减少。综合权衡时间及精度两方面，本文算法较上述两种算法更具优越性。综上所述，本文提出了一种耗时短、精确度高、拼接效果良好的图像拼接方法。

[1] GHOSH D and KAABOUCH N. A survey on image mosaicing techniques[J].&, 2015, 34(C): 1-11. doi: org/10.1016/ j.jvcir.2015.10.014.

[2] 张宝龙, 李洪蕊, 李丹, 等. 一种针对车载全景系统的图像拼接算法的仿真[J]. 电子与信息学报, 2015, 37(5): 1149-1153. doi: 10.11999/JEIT141185.

ZHANG Baolong, LI Hongrui, LI Dan,. A simulation of image mosaic algorithm based on vehicle panorama system[J].&, 2015, 37(5): 1149-1153. doi: 10.11999/JEIT141185.

[3] XIE X, XU Y, LIU Q,. A study on fast SIFT image mosaic algorithm based on compressed sensing and wavelet transform[J].&, 2015, 6(6): 835-843. doi: org/10.1007/s12652- 015-0319-2.

[4] 余先川, 吕中华, 胡丹. 遥感图像配准技术综述[J]. 光学精密工程, 2013, 21(11): 2960-2972.doi: 10.3788/OPE.20132111. 2960.

YU Xianchuan, LÜ Zhonghua, and HU Dan. Review of remote sensing image registration technique[J]., 2013, 21(11): 2960-2972. doi: 10.3788/ OPE.20132111.2960.

[5] AGHAJANI K, YOUSEFPOUR R, SHIRPOUR M,. Intensity based image registration by minimizing the complexity of weighted subtraction under illumination changes[J].&, 2016, 25: 35-45. doi: org/10.1016/j.bspc.2015.10.009.

[6] 赵春阳, 赵怀慈. 多模态鲁棒的局部特征描述符[J]. 光学精密工程, 2015, 23(5): 1474-1483. doi: 10.3788/OPE.20152305. 1474.

ZHAO Chunyan and ZHAO Huaici. Multimodality robust local feature descriptors[J]., 2015, 23(5): 1474-1483. doi: 10.3788/OPE.20152305.1474.

[7] 颜雪军, 赵春霞, 袁夏. 一种鲁棒的基于图像对比度的局部特征描述方法[J]. 电子与信息学报, 2014, 36(4): 882-887. doi: 10.3724/SP.J.1146.2013.00846.

YAN Xuejun, ZHAO Chunxia, and YUAN Xia. A robust local feature descriptor based on image contrast[J].&, 2014, 36(4): 882-887. doi: 10.3724/SP.J.1146.2013.00846.

[8] WANG Weixing, CAO Ting, LIU Sheng,. Remote sensing image automatic registration on multi-scale harris- laplacian[J]., 2015, 43(3): 501-511. doi: org/10.1007/s12524-014-0432-2.

[9] LOWE D G. Object recognition from local scaleinvariant features[C]. Proceedings of the 7th International Conference on Computer Vision, Corfu, Greece, ICCV, 1999, 2: 1150-1157.

[10] LOWE D G. Distinctive image features from scale-invariant key points[J]., 2004, 60(2): 91-110.doi: org/10.1023/B:VISI.0000029664.99615.94.

[11] CALONDER M, LEPETIT V, STRECHA C,. BRIEF: Binary Robust Independent Elementary Features[C]. European Conference on Computer Vision, Springer Berlin Heidelberg, Germany, 2010: 778-792. doi: org/10.1007/ 978-3-642- 15561-1_56.

[12] LEUTENEGGER S, CHLI M, and SIEGWART R Y. BRISK: Binary Robust Invariant Scalable Keypoints[C]. International Conference on Compater Vision, Barcelona, Spain, 2011: 2548-2555. doi: org/10.1109/ICCV.2011.6126542.

[13] KASHIF M, DESERNO T M, HAAK D,. Feature description with SIFT, SURF, BRIEF, BRISK, or FREAK? A general question answered for bone age assessment[J]., 2015, 68: 67-75. doi: org/10.1016/j.compbiomed.2015.11.006.

[14] ZHU Jun and REN Mingwu. Image mosaic method based on SIFT features of line segment[J]., 2014, 2014(6): 926312.doi: org/10.1155/2014/926312.

[15] ZHAO Chunyang, ZHAO Huaici, LÜ Jinfeng,. Multimodal image matching based on multimodality robust line segment descriptor[J]., 2016(177): 290-303. doi: org/10.1016/j.neucom.2015.11.025.

[16] 黄立勤, 陈财淦. 全景图拼接中图像融合算法的研究[J]. 电子与信息学报, 2014, 36(6): 1292-1298. doi: 10.3724/SP.J.1146. 2013.01220.

HUANG Liqin and CHEN Caigan. Study on image fusion algorithm of panoramic image stitching[J].&, 2014, 36(6): 1292-1298.doi: 10.3724/SP.J.1146.2013.01220.

Image Mosaic Algorithm Based on Improved BRISK

DONG Qiang①②LIU Jinghong①WANG Chao③ZHOU Qianfei①②

①(,,,130033,)②(,100049,)③(77110’,618400,)

In order to obtain accurate aerial stitching images,this paper proposes a novel image mosaic method based on Binary Robust Invariant Scalable Keypoints (BRISK) feature of directed line segment, aiming to resolve incident scaling, rotation, changes in lighting condition, the low correct matching rate and low accuracy using conventional BRISK algorithm in image mosaic. This method firstly uses BRISK algorithm to match in order to acquire rough point matching. Secondly, it constructs directed line segments, describes them with BRISK feature, and matches those directed segments.The method is used to purified point matching based on statistical voting. Finally, weighted fusion and luminance equalization are used to image fusion to accomplish image mosaic. The experiment results show that the method has strong robustness and stability for lighting, rotation, resolution and scaling. The proposed method has high precision, and can achieve fine image mosaic results.

Image registration; Image mosaic;Binary Robust Invariant Scalable Keypoints (BRISK) feature; Nearest-neighbor line segments

TP7221

A

1009-5896(2017)02-0444-07

10.11999/JEIT160324

2016-04-05；改回日期：2016-10-11；

2016-12-02

刘晶红 liu1577@126.com

吉林省重大科技攻关项目(11ZDGG001)，国家林业公益性行业科研专项(201204515)

The Key Science and Technology Project of Jilin Province (11ZDGG001), The Forestry Industry Scientific Research for National Public Welfare Projects (201204515)

董 强： 男，1989 年生，博士生，研究方向为遥感图像拼接技术.

刘晶红： 女，1967 年生，研究员，研究方向为机载光电成像测量设备.

王 超： 男，1983 年生，工程师，研究方向为无人机技术.

周前飞： 男，1989 年生，博士生，研究方向为航空光电成像畸变校正技术.