NaNO3-KNO3-NaNO2三元混合相变熔盐结构与物性的分子动力学模拟
2017-10-13倪海欧路贵民于建国
倪海欧,孙 泽,路贵民,于建国
NaNO3-KNO3-NaNO2三元混合相变熔盐结构与物性的分子动力学模拟
倪海欧,孙 泽,路贵民,于建国
(华东理工大学国家盐湖资源综合利用工程技术研究中心,上海200237)
相变熔盐目前是太阳能热发电的重要传蓄热介质,其结构和性质之间的定量关系是相变熔盐研究的热点。本文采用分子动力学方法,利用Buckingham势函数,对NaNO3-KNO3-NaNO2三元混合熔盐的结构和性质进行了研究。计算了混合熔盐在不同温度下的径向分布函数、配位数、角分布函数等结构信息,以及密度、剪切黏度、热导率、比热容等性质。结果表明,计算得到的各项性质与文献值吻合较好,验证了势函数和计算方法的可靠性,为计算机模拟指导熔盐配方、熔盐构效关系定量研究奠定了基础。
分子动力学;熔盐结构;熔盐物性
随着能源问题越来越成为当今世界所关注的一大重要议题,太阳能光热发电作为一种绿色可持续的能源形式,正受到越来越广泛的关注。我国已在“十二五”期间启动示范项目,“十三五”规划到2020年光热发电装机容量达到500万千瓦[1],光热发电正进入一个快速发展期。
熔盐作为一种廉价、高效的传蓄热介质,在太阳能热发电等领域有着重要的应用[2-3]。但是,由于熔盐的高温特性,其物性的实验测试成本高、难度大、精度低,对测试仪器的伤害也很大。而随着计算机科学的飞速发展,计算机模拟可以处理的体系越来越大,计算精度也越来越高,在很多情况下可以作为传统实验的替代和补充,尤其适合熔盐这种高温高腐蚀的场合。LYNDEN-BELL等[4]用分子动力学方法计算了NaNO2的晶格振动。PENG等[5]用第一性原理方法计算了KNO2固体的Debye温度、比热容、声子速度、声子平均自由程、声子热导率等性质。JAYARAMAN等[6]利用分子动力学方法计 算了Li、Na、K三种碱金属硝酸盐的密度、黏度、 热导率、比热容、熔点等性质。URAHATA等[7]采用带有极化模型的分子动力学方法计算了LiNO3的一些性质,并比较了极化模型与经典模型计算结果的差异。
本文通过经典分子动力学模拟的方法计算了质量比为7∶53∶40的NaNO3-KNO3-NaNO2三元混合熔盐。这种熔盐通常被称为HITEC,在工业上有着广泛的应用。本文计算了HITEC熔盐的结构与性质,包括径向分布函数、角分布函数、密度、剪切黏度、热导率、比热容等,并与文献中的实验值进行了比较,验证了势函数和计算方法的可靠性。
1 分子动力学计算
1.1 力场模型
采用Buckingham势函数来描述模拟体系分子间库仑相互作用、短程排斥作用和范德华耗散作用,如式(1)所示
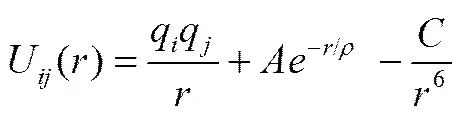
式中,q、q为原子电荷,为原子间距离,r为截断半径,、为短程斥力的力场参数,为耗散系数。混合熔盐中,硝酸钠和硝酸钾采用文献[8]中的势函数,亚硝酸钠采用文献[4]中的势函数。势函数参数见表1(硝酸根中的N和O以N3、O3表示,亚硝酸根中的以N2、O2表示,下文均用这种方法表示)。对于交叉项,采用如下交叉法则:A= (AA)1/2,C= (CC)1/2,2/ρ=1/ρ+1/ρ。
硝酸根与亚硝酸根的分子内作用力的力常数由拉曼光谱数据计算得出[9-10],N—O键采用Harmonic简谐势,如式(2)所示,式中为N—O键长,0为平衡键长,K为力常数;O—N—O键角采用Charmm势,如式(3)所示,其中第一项为O—N—O键角弯曲的简谐项,第二项为O—O非键排斥项。式中为O—N—O键角,0为平衡键角,K为力常数,为O—O距离,UB为平衡距离,UB为Urey Bradley力常数。具体参数见表2。

(3)
1.2 计算方法
模拟计算使用开源计算软件Lammps进行。采用周期性边界条件,总粒子数为5540个,其中含有685个Na+、543个K+、628个、600个。势函数截断半径取模拟盒子边长的一半。长程作用力采用pppm求和法,计算精度设置为10-4。时间步长取1fs。

表1 分子间势函数参数

表2 分子内势函数参数
2 结果与讨论
2.1 径向分布函数
径向分布函数(radical distribution function,RDF)是描述流体结构特征最重要的函数,其定义如式(4)所示,其中β为β粒子的数密度,αβ()表示位于以α粒子为中心、为半径的球体内β粒子的平均数。
图1是阳-阳离子对的RDF。从图中可以看出,随着温度的上升,RDF第一峰的高度逐渐降低,第一峰峰谷的高度逐渐增大,峰变得更平,峰位置右移,而RDF的整体形貌没有发生明显变化。图2是阳-阴离子对的RDF,同样的,随着温度的升高,峰趋向于展平,但峰位置没有明显变化。这是由于温度的升高,离子之间相互作用减弱,分子运动随机性变大,分子微观团簇变得有所松散。而温度的升高使得同号离子之间距离变大,导致峰位置右移,但异号离子之间库仑引力较强,温度的升高对其离子间距离并没有明显影响。
图3是623 K下异号离子对的RDF。从图中可以看出,Na-N3和K-N3的峰高基本一致,而Na-N3峰位置比K-N3更小,两者峰位置之差是由于Na的离子半径小于K,导致Na-N之间距离更近。而Na-N2的峰高明显高于K-N2,两者第一峰位置的差异也相对较大,这可能是源于Na+与的相互作用更强,两者结合得更加紧密。
配位数是描述熔盐结构最重要得参数之一,如式(5)所示,可由径向分布函数得积分得到。表3列出了M-N离子对的配位数。可以看出,随着温度的升高,所有的离子对的配位数均变小了,这说明随着温度的升高,微观层面上离子团簇变得松散。同时,M-N3离子对的配位数比M-N2离子对大,这是由于体系中的数量多于。对不同的阳离子,Na-N的配位数小于K-N,而在径向分布函数中Na-N的峰高于K-N,这说明虽然K的第一配位壳层内阴离子个数比Na多,但是和Na相比结合的更为松散。

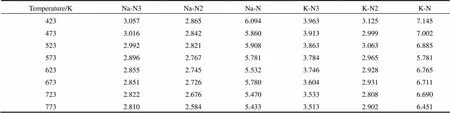
表3 阳-阴离子的配位数
2.2 角分布函数
径向分布函数在描述液体局域结构中起着至关重要的作用,但是其只描述了粒子之间的配对状况,而没有描述其团簇结构内部粒子之间的取向信息。为了获取团簇内部的取向信息,在径向分布函数的基础上,本文还计算了体系阴-阳-阴离子的角度分布函数(angular distribution function,ADF),以反映“键”的取向[11]。
图4为混合熔盐中N-M-N“键角”的角分布函数(M指代Na和K)。从图中可以看出N-M-N“键角”主要分布在40°~180°之间,在90°附近分布最为密集,说明在熔盐中M-N“键角”的取向并不是无规律的,而是倾向于形成松散的八面体配位结构。
图5选取了623 K下N-M-N角分布函数,可以看出对相同的阳离子,N3-M-N3和N2-M-N2的角分布没有明显差别。而对不同的阳离子,N-Na-N的峰比N-K-N的峰更高,且更接近90°,说明Na-N的八面体配位构型比K-N更为显著。N-K-N的峰小于90°也和K-N的配位数超过6吻合。
2.3 密 度
密度计算在NPT系综下进行,每个温度点共计算200万步,然后对每一步输出的密度值进行平均,得到该温度下熔盐密度的模拟值。模拟值与文献值的对比如图6所示,两者的偏差小于3%。密度的文献值采用Serrano-López[12]总结的关联式,以下剪切黏度、比热容的文献值均采用该文献的值。
2.4 剪切黏度
熔盐的剪切黏度采用平衡分子动力学方法计算,根据Green-Kubo公式,由模拟体系应力张量自相关函数(Stress Tensor Auto-Correlation Function)计算出体系的剪切黏度,如式(6)所示。式中B为波尔兹曼常数,、为体系的温度和体积,S为应力张量的分量。应力张量的每一个非对角分量(S,S,S)都可以计算出一个剪切黏度值,最终计算值取这三个值的平均数。

剪切黏度的计算在NVT系综下进行,自相关函数的相关长度取8ps,总共计算1000万步。
剪切黏度计算值与实验值的比较见图7,其中红色的曲线为文献值,蓝色的曲线为模拟值的拟合曲线,拟合曲线与文献值的平均误差小于5%。拟合得到的黏度-温度关联式如下:

2.5 热导率
热导率同样采用平衡分子动力学计算方法,根据Green-Kubo公式,由模拟体系热流通量自相关函数(Heat Flux Auto-Correlation Function)计算出体系的热导率,如式(8)所示。式中B为波尔兹曼常数,为体系的温度,Ex为热流分量E的方向分量。热流通量在、、方向上的每一个分量都可以计算出一个热导率值,最终计算值取这3个值的平均数。
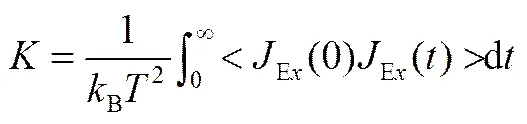
热导率的计算在NVT系综下进行,自相关函数的相关长度取8ps,共计算1000万步。
热导率的计算值与文献值的对比见图8,其中红色实线为Serrano-López[12]总结的数据库中的推荐值,虚线为其它文献[13-15]中报道的热导率值,可见不同文献报道的热导率的值差异很大,本文得到的计算值与Serrano-López所总结的推荐值之间的平均偏差约24%,考虑到本文所采用的经典分子动力学方法,此误差在可接受范围内。
2.6 比热容
比热容通过体系总能量的涨落来计算,如式(9)~(10)所示。恒容比热容在NVT系综下进行,恒压比热容在NPT系综下进行。式中(2)=(2)-()2,为体系总能量。总共计算200万步。

比热容计算值见表4,将不同温度下的C进行平均之后得到熔盐的比热容为1428.141 J/(kg·K),文献值为1561 J/(kg·K),计算值与文献值相比偏差为8.5%,两者吻合得较好。
1.3 常规治疗 术后给予止血、预防感染、补液等治疗,补液量在3000 mL左右,采用头低脚高位,头偏向患侧,术后第3天给予阿托伐他汀钙片20 mg口服,每日1次。根据引流情况术后3 d内拔除引流管。

表4 熔盐的定压比热容计算值
3 结 论
本文利用Buckingham势函数对NaNO3-KNO3- NaNO2三元混合熔盐进行了分子动力学计算。径向分布函数、配位数与角分布函数计算结果表明,随着温度的升高,离子间相互作用减弱,离子团簇变得松散,且异号离子之间距离变大,而同号离子间距没有明显变化。配位数与角分布函数表明混合熔盐中阴阳离子呈六配位八面体构型,且Na-N的八面体构型比K-N更为显著。同时本文对熔盐密度、剪切黏度、热导率、比热容进行了模拟计算,并与文献值进行了对比。结果表明,计算值与文献值均吻合得很好,验证了本文所采用的势函数与计算方法的可靠性,为下一步大规模计算模拟熔盐配方提供了研究基础。
[1] 国家能源局. 太阳能发展“十三五”规划[R]. 2016.
[2] VIGNAROOBAN K, XU X, ARVAY A, et al. Heat transfer fluids for concentrating solar power systems—A review[J]. Applied Energy, 2015, 146: 383-396.
[3] NUNES V M B, QUEIRÓS C S, LOURENÇO M J V, et al. Molten salts as engineering fluids—A review[J]. Applied Energy, 2016, 183: 603-611.
[4] LYNDEN-BELL R M, IMPEY R W, KLEIN M L. Investigation of the lattice vibrations of solid NaNO2by means of molecular dynamics calculations[J]. Chemical Physics, 1986, 109(1): 25-33.
[5] PENG Q, DING J, WEI X, et al. First-principles study for thermodynamic properties of solid KNO2system[J]. International Journal of Thermophysics, 2015, 36(10/11): 2833-2844.
[6] JAYARAMAN S, THOMPSON A P, VON LILIENFELD O A, et al. Molecular simulation of the thermal and transport properties of three alkali nitrate salts[J]. Industrial & Engineering Chemistry Research, 2010, 49(2): 559-571.
[7] URAHATA S R M, RIBEIRO M C C. Molecular dynamics simulation of molten LiNO3with flexible and polarizable anions[J]. Physical Chemistry Chemical Physics, 2003, 5(12): 2619-2624.
[8] RIBEIRO M C C. On the Chemla effect in molten alkali nitrates[J]. The Journal of Chemical Physics, 2002, 117(1): 266-276.
[9] JANZ G J, JAMES D W. Raman spectra and ionic interactions in molten nitrates[J]. The Journal of Chemical Physics, 1961, 35(2): 739-745.
[10] HISATSUNE I C, DEVLIN J P, CALIFANO S. Urey-Bradley potential constants in nitrogen dioxide, nitrite and dinitrogen tetroxide[J]. Spectrochimica Acta, 1960, 16: 450-458.
[11] WANG J, SUN Z, LU G, et al. Molecular dynamics simulations of the local structures and transport coefficients of molten alkali chlorides[J]. The Journal of Physical Chemistry B, 2014, 118(34): 10196-10206.
[12] SERRANO-LÓPEZ R, FRADERA J, CUESTA-LÓPEZ S. Molten salts database for energy applications[J]. Chemical Engineering and Processing: Process Intensification, 2013, 73: 87-102.
[13] JANZ G J, TOMKINS R P T. Physical properties data compilations relevant to energy storage. IV. Molten salts: Data on additional single and multi-component salt systems[R]. U.S. Department of Commerce, 1981.
[14] WU Y, CHEN C, LIU B, et al. Investigation on forced convective heat transfer of molten salts in circular tubes[J]. International Communications in Heat and Mass Transfer, 2012, 39(10): 1550-1555.
[15] OMOTANL T, NAGASHLMA A. Thermal conductivity of molten salts, HTS and the LiNO3-NaNO3system, using a modified transient hot-wire method[J]. J. Chem. Eng. Data, 1984, 29: 1-3.
Molecular dynamics simulation of structure and physical properties of NaNO3-KNO3-NaNO2ternary phase-change molten salts
NI Haiou, SUN Ze, LU Guimin, YU Jianguo
(National engineering research center for comprehensive utilization of salt lake resources, East China University of Science and Technology, Shanghai 200237, China)
Phase-change salt is an important heat transfer and storage material for concentrated solar power plants. This calls for a quantitative understanding of the relationship between the structure and properties of molten salts. We performed molecular dynamics simulations on NaNO3-KNO3-NaNO2ternary molten salts using Buckingham potential with an aim to understand such relationship. The simulations gave structural information such as radical distribution function, coordination number and angular distribution function, and physical properties including density, shear viscosity, thermal conductivity and heat capacity. The results showed that all the properties calculated agree well with the literature data, suggesting the reliability of pair potential and simulation method used in the work.
molecular dynamics simulation; structure; physical property
10.12028/j.issn.2095-4239.2017.0060
TB 34
A
2095-4239(2017)04-669-06
2017-05-03;
2017-05-16。
国家自然科学基金(U1407126);青海省应用基础研究(2017- ZJ-727);青海省重大科技专项(2013-G-A1A-3)。
倪海欧(1988—),男,主要研究方向为相变材料,E-mail:nihaiou@foxmail.com;
孙泽,博士,副教授,研究方向为熔盐储能,化工过程模拟,E-mail:zsun@ecust.edu.cn;路贵民,教授,研究方向为熔盐离子结构,盐湖资源综合利用等,E-mail:gmlu@ecust.edu.cn。
