蒙特卡洛方法在坦克火控系统误差分析中的应用

王 东， 陈晚如， 杜 宏 ， 马 骁

(1.中国人民解放军驻201所军代室，北京 100072；2.中国北方车辆研究所，北京 100072 )

蒙特卡洛方法在坦克火控系统误差分析中的应用

王 东1， 陈晚如2， 杜 宏2， 马 骁2

(1.中国人民解放军驻201所军代室，北京 100072；2.中国北方车辆研究所，北京 100072 )

影响坦克火控系统总体精度的误差源众多，且各误差源误差值随着时间的推移呈现随机分布.为了找出各误差源的误差值与系统总误差的关系，及所谓的误差传递关系，应用蒙特卡洛法建立了火控系统的误差分析数学模型.应用该模型模拟仿真实际射击，得到了火控系统输入量误差与输出量误差之间的传递关系，结果表明输入量误差对高低分量的影响大于水平分量，从而找到影响射击精度的主要误差源.

火控系统；误差分析；蒙特卡洛法；圆概率偏差

Abstract：There are many sources of input error affecting the tanker′s fire control system′s total precision, and the input errors present random distribution over time. In order to find out the relationship between input errors and the total system error, which is called error transfer relation，the total fire control system error analysis mathematical model is established by using the Carlo method. It can simulate actual shooting to obtain the error transfer relation between inputs and outputs. The result shows that the vertical input error affects more than the horizontal input error and can be rergarded as the primary error source which influences the shooting precision.

Keywords: fire control system; error analysis; Monte Carlo method; circle probable error

误差分析是对火控系统的精度进行合理分配的前提, 其主要工作就是全面、合理地分析整个系统的误差源, 并找出各误差源与系统总误差的关系, 即所谓的误差传递关系.然后,对偏离目标产生的原因、后果及发生的阶段进行分析，找出主要的误差源，把误差减少到最低限度.

由于坦克火控系统包含的分系统、部件或元器件很多, 所以影响火控系统总体精度的误差源很多, 且各误差源误差值随着时间的推移是随机的，服从一定的概率统计分布.因此, 火控系统的误差分析是一个繁杂的、反复的过程.蒙特卡洛方法[1]又称“统计试验法”，是一种解算数学和物理问题的近似计算方法.该方法能够直接地反映被研究系统的随机性.徐卫良等作者利用蒙特卡洛技术模拟具有任意概率分布的原始误差，抽样计算机器人手部位姿误差数模[2]；赵永涛等作者根据导航机器人的误差数学模型，利用蒙特卡洛方法对导航机器人的位姿精度进行了分析[3].

本研究以某型坦克火控系统作为研究对象，应用蒙特卡洛方法计算火控系统输出量标称值、输入量和输出量的抽样值，通过N次模拟得到瞄准点方位分量误差和高低分量误差的N个抽样值，最终得到平面坐标系中的圆概率偏差，从而找到影响射击精度的主要误差源.

1 火控系统误差计算数学模型的建立

蒙特卡洛法(Monte Carlo Method)是一种通过随机变量的统计实验、求解工程技术问题近似解的数值方法.下面应用蒙特卡洛方法对影响火控系统的射击精度进行分析，并建立火控系统误差计算数学模型.

1.1 火控系统输出量标称值的计算

火控系统误差的计算在二维平面内进行.设在平面坐标系统中瞄准点的方位或高低量为y；火控系统的n维输入参数向量为x1,x2,…,xn，它们之间的函数关系可以表示为

y=f(x1,x2,…,xn).

(1)

若综合火控系统输入参数不存在误差，那么根据系统输入量的标称值，可计算得到系统输出量的标称值y0=f(x10,x20,…,xn0)，其中，x10,x20,…,xn0为综合火控系统n维输入参数向量的标称值.

1.2 仿真产生输入量的抽样值

在实际综合火控系统中，输入量是由各个有关的传感器提供的.由于各种随机因素的影响，n维输入向量X带有误差，而误差分析的目的就是分析计算各个输入量误差对综合火控系统输出的影响，即求解在存在输入误差的条件下，系统输出的误差.

一般输入量可用公式(2)来描述.

xi=xi0+△xi.

(2)

式中：xi0为第i个输入量的标称值；△xi为第i个输入量的随机误差；i=1,2,…,n.

根据中心极限定理，工程上可将随机误差△xi处理为正态随机变量，即

△xi～N(μi,σi).

(3)

式中：μi为第i个输入量随机误差的均值；σi为第i个输入量随机误差的均方差.

1.3 系统输出量抽样值的计算

因此，当综合火控系统输入参数存在误差时，系统的第k次模拟产生的实际输出为

yk=f(x1k,x2k,…,xnk)=
f(x10+△x1k,x20+△x2k,…,xn0+△xnk).

(4)

式中：k=1,2,…,n.

Xk=(x1k,x2k,…,xnk)表示第k次模拟产生的输入随机向量；ΔXk=(△x1k,△x2k,…,△xnk)为第k次模拟产生的输入随机误差向量.

1.4 系统输出误差抽样值计算

系统第k次模拟产生的输出误差为：

△yk=yk-y0.

(5)

式中：y0为系统输出量的标称值；yk为考虑所有误差源后系统的第k次模拟输出量.

这样，通过n次模拟，就可以得到系统输出误差的n个抽样值：

{△y1,△y2,…,△yn}.

(6)

1.5 误差指标的统计计算

按照上述方法，通过n次模拟，可以得到瞄准点方位分量误差和高低分量误差的n个抽样值：

{ΔFWk,ΔGDk}.

(7)

式中：ΔFWk为第k次模拟产生的瞄准点方位分量误差；ΔGDk为第k次模拟产生的瞄准点高低分量误差；k=1,2,…,n.

根据数理统计和概率论知识，可得到瞄准点方位分量误差的均值E(ΔFW)和高低分量误差的均方差E(ΔGD).则瞄准点方位分量误差的均方差(Root-Mean-Square，简称RMS)RMS(ΔFW)和高低分量误差的均方差RMS(ΔGD)为：

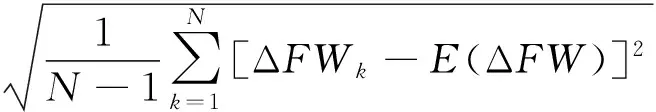
(8)

(9)

1.6 圆概率偏差的计算

综合火控系统的精度指标之一圆概率偏差，其定义为：在平面坐标系内，以瞄准点方位和高低分量的标称值(或平均瞄准点)为中心、以R为半径的一个圆.如果瞄准点二维随机变量出现在该圆中的概率为50%，则称此圆的半径R为概率偏差，记作RCEP.

瞄准点脱靶量是标称瞄准点与实际瞄准点之间的距离.第k次模拟产生的瞄准点脱靶量计算模型为：

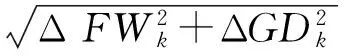
(10)

通过n次模拟，可以得到瞄准点脱靶量的n个抽样值：{Δ1,Δ2,…,Δk}(k=1,2,…,n).首先将瞄准点脱靶量按从小到大排列所有的仿真结果，得到瞄准点脱靶序列：

{Δ1,Δ2,…,Δ0.5(n-1),Δ0.5n,Δ0.5(n+1),…,Δn}.

(11)

则当n为偶数时，

RCEP=0.5[Δi=0.5n+Δi=0.5(n+1)];

(12)

当n为奇数时，

RCEP=Δi=0.5(n-1).

(13)

式中：i为按脱靶量Δi增加顺序排列时的脱靶量编号.

2 仿真模型的建立

坦克火控系统射击过程依次为瞄准、跟踪、解算、调炮、击发和验靶.其组成包括目标观瞄子系统、火控计算机子系统和火炮控制子系统[2].坦克火控系统的各误差源误差值随着时间的推移是随机的，服从一定的概率统计分布，图1是在MATLAB/Simulink中搭建的火控系统误差仿真模型.该模型包含火控系统的所有输入源及引入误差环节，能够反映出误差对精度的传递关系.

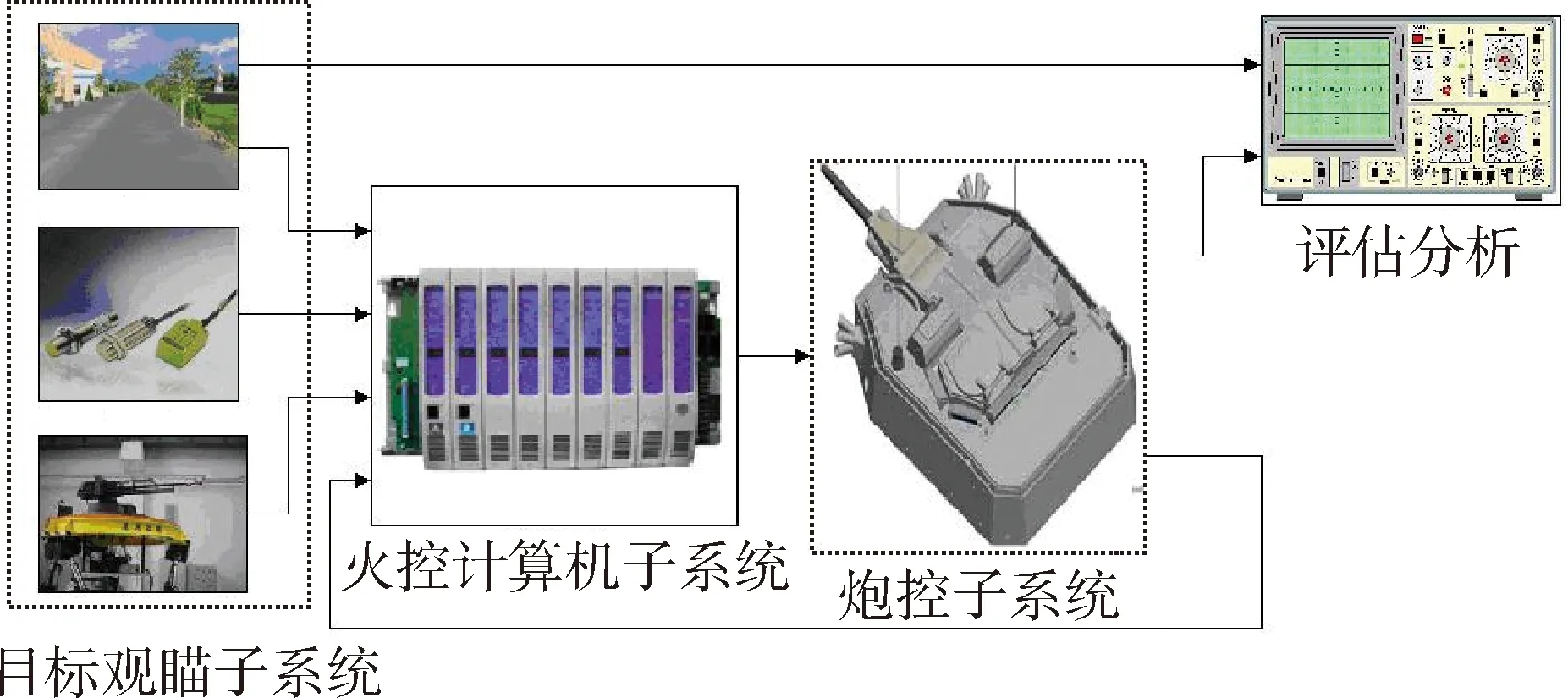
图1 坦克火控系统火控系统误差仿真模型

由图1可见火控系统的误差源包括以下三部分：

1)目标观瞄子系统中的误差源主要有：测量目标距离、高低角和方位角的3个传感器；目标跟踪误差，目标状态预测误差，瞄准线稳定和漂移误差，机动目标模型误差，等等.

2)火控计算机子系统中的误差源主要有：由于横风风速对弹丸的飞行影响很大，所以横风传感器是弹道解算阶段的主要误差源.另外，药温偏差、炮膛磨损、弹重、装药量，还有环境因素包括气温、气压、横风和地形，射弹散布，弹道解算模型及修正误差，等等.

3)炮控子系统中的误差源主要有：火炮零位测量误差、火炮位置测量误差、火炮稳定误差、火炮身管变形.

3 仿真实验

设定仿真条件如下：目标距离为1 800 m，药温为21 ℃，气温为15 ℃，气压为一个标准大气压.取仿真次数为3 000次.分别考虑如下两种情况：

1)火控计算机子系统输入误差分析，即只考虑火控计算机子系统输入量引入的误差；

2)坦克火控系统总输入量误差的分析，即目标观瞄子系统、火控计算机子系统和炮控子系统所有误差源对瞄准点精度的影响.

在MATLAB/Simulink中分别就以上两种情况进行仿真计算，得到瞄准点位置.瞄准点位置的分布图如图2和图3所示.

图2 计算机子系统输入量误差的圆概率偏差图

图3 火控系统输入量误差的圆概率偏差图

同时得到瞄准点方位分类误差E(ΔFW)、瞄准点高低分量误差E(ΔGD)、瞄准点脱靶量最小值和最大值、以及瞄准点方位分量和高低分量的均方差RMS、最后得到瞄准点分布的圆概率偏差RCEP.各项数据见表1.

从表1中各项数据可知，当只考虑火控计算机子系统输入量误差时，瞄准点方位分量误差和高低分量误差均较小.而考虑整个火控系统输入误差时，瞄准点高低分量误差增大了3.29倍，水平分量误差增大了1.3倍.同时当只考虑火控计算机子系统误差输入时，瞄准点以50%的概率分布在半径为0.084的圆内；考虑坦克火控系统整体误差输入时，圆的半径增大为0.241，圆概率偏差RCEP增大了2.87倍.由此可以得出，目标观瞄子系统和炮控子系统的误差输入量对高低分量的影响要大于水平分量，应该把减小目标观瞄子系统和炮控子系统高低分量误差作为提高火控系统精度的一个重点研究方向.

表1误差分析结果对比表

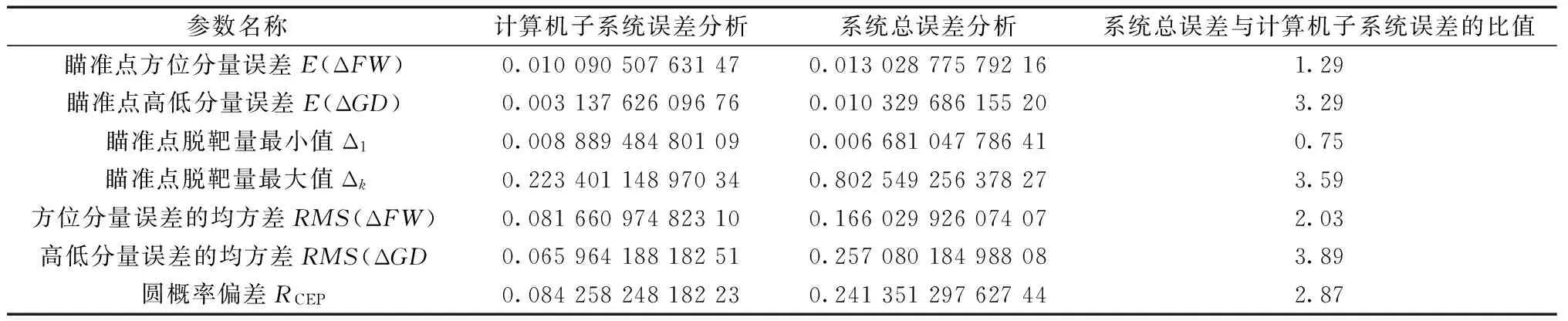
参数名称计算机子系统误差分析系统总误差分析系统总误差与计算机子系统误差的比值瞄准点方位分量误差E(ΔFW)0.010090507631470.013028775792161.29瞄准点高低分量误差E(ΔGD)0.003137626096760.010329686155203.29瞄准点脱靶量最小值Δ10.008889484801090.006681047786410.75瞄准点脱靶量最大值Δk0.223401148970340.802549256378273.59方位分量误差的均方差RMS(ΔFW)0.081660974823100.166029926074072.03高低分量误差的均方差RMS(ΔGD0.065964188182510.257080184988083.89圆概率偏差RCEP0.084258248182230.241351297627442.87

某次实弹动对动射击试验，车速保持在20 km/h左右，一共发射了9发弹，图4为弹着点分布图.此时影响射击精度的误差源增加了很多，包括车体的振动、炮口的振动等因素.经计算得到圆概率偏差RCEP为0.861 0，方位向的偏差均方差为0.590 1，高低向的偏差均方差为0.938 2，显然弹着点在高低方向的偏差要大于方位向的偏差，所以要将减小高低分量误差作为提高火控系统精度的一个重点研究方向.这与上面的仿真结果一致.

图4 某次试验射击实验弹着点分布图

4 结 论

以某型坦克火控系统作为研究对象，应用蒙特卡洛方法计算了火控系统输出标称值、输入量和输出量的抽样值，通过N次模拟得到了瞄准点方位分量误差和高低分量误差的N个抽样值，最终得到了平面坐标系中的圆概率偏差，从而可以方便地找到影响射击精度的主要误差源.通过研究得到以下结论：

1)采用“蒙特卡洛”随机模拟法,模拟实际的坦克火力控制系统的各个误差源及其传递的关系，提供了一种利用计算机仿真来分析各误差源对火控系统精度影响敏感程度的方法.

2)得出的部分误差源的仿真结果与实际测试结果一致,其变化趋势对于改进误差源是很有参考意义的，甚至可以对单个传感器的误差进行评价，得到其贡献值，从而指导传感器的改进，达到效果和成本的最佳.

3)利用蒙特卡洛方法，得到各误差源对系统总误差的权系数,再应用最优或专家系统的方法就可以得到火控系统的精度分析方案，可以很好地指导实际工作.通过这样的仿真试验，可以得到各个子系统对精度的贡献值，指导系统指标分配.

[1] 裴鹿成，王仲奇.蒙特卡洛方法及其应用[M]. 北京：海洋出版社：1993-1997.

[2] 徐卫良，张启先. 机器人误差分析的蒙特卡洛方法[J]. 机器人，1988，(4)：3-8.

[3] 赵永涛，王田苗，孙 磊. 基于蒙特卡洛方法的导航机器人的误差分析[J]. 航空制造技术，2004，(3)：52-54.

ApplicationofMonteCarloMethodinErrorAnalysisofTankFireControlSystem

WANG Dong， CHEN Wan-ru， DU Hong， MA Xiao

(1. People′s Liberation Army in 201 Military Representative Room, Beijing 100072，China；2. China North Vehicle Research Institute, Beijing 100072，China)

TJ81+0.376；TJ81+0.1

A

1009-4687(2017)03-0036-04

2017-04-14.< class="emphasis_bold">网络出版时间

时间：2017-07-13.

10.16599/j.cnki.1009-4687.20170713.001

王 东(1968-)，男，研究方向为坦克装甲车辆.

http：//kns.cnki.net/kcms/detail/11.4493.TH.20170713.1124.002.html