船舶电力系统无功优化的GSA-IPM算法

唐卓贞



船舶电力系统无功优化的GSA-IPM算法

唐卓贞

（南通航运职业技术学院，江苏南通 226010 ）

提出GSA-IPM（万有引力-内点）算法求解船舶电力系统无功优化问题，以降低船舶电力系统的有功损耗，提高电压质量，改善安全经济运行水平。将算法应用于某实际船舶电力系统进行仿真测试，结果与万有引力搜索算法（GSA）、遗传算法（GA）及粒子群算法（PSO）作比较，证明了算法能够使有功网损更低，电压质量更佳，从而验证了方法的有效性。

船舶工程 船舶电力系统 无功优化 GSA-IPM算法

0 引言

大规模大容量的电力系统在船舶工业领域不断得到应用，以及在船舶电力系统的特殊地位，其安全稳定性至关重要。为了改善船舶电力系统的经济安全运行状况，降低系统有功损耗，改善电能的质量，进一步开展无功优化的分析、研究显得日益迫切。

船舶电力系统无功优化问题是包含多个变量、约束的混合非线性规划问题，求解这类问题有智能算法[1]与数值算法[2]两类。前者较擅于处理连续性优化问题，但在处理离散变量时具有明显不足。后者对于离散变量的处理显著优于前者，但易陷于局部最优解。万有引力搜索算法（GSA）[3,4]作为新近提出的启发式算法，已被证明较其它同类算法具有更好的鲁棒性，并能取得更佳的优化结果，而现代内点法（IPM）则以求解大规模非线性规划问题著称。

结合GSA与IPM提出了一种求解船舶电力系统无功优化的新型混合算法，并对所建立的船舶电力系统无功优化模型进行了求解。

1 船舶电力系统无功优化

1.1 电力系统无功优化

无功优化问题是一个含有多变量（离散与连续）、多约束（发电机机端电压、变压器分接头的调节以及电容器组的投切）的复杂非线性规划问题。

无功优化的数学表示如下：

1.2 船舶电力系统无功优化

船舶电力系统是孤立系统，与陆上电力系统有诸多差异，如输电方式、系统容量和负荷类型等，船舶电站供给的负荷通常分为船舶用电设备的负荷（动力用电、生活用电）与其它功率损耗（线路阻抗等功率损耗）两部分。其中的无功负荷主要是电动机的感性负载。

船舶电力系统无功优化数学模型可表述如下。

2 GSA-IPM算法

2.1 万有引力算法原理

万有引力搜索算法于2009年由Rashedi等人提出，该算法是受牛顿万有引力定律和运动定律的启发。该算法认为，任何粒子间均以万有引力相互作用，该作用力使所有粒子趋向于质量更大的粒子运动。由此，更重的粒子的适应度值更高，它的位置即对应于更优解。

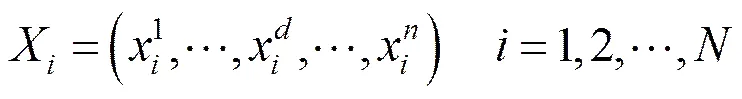
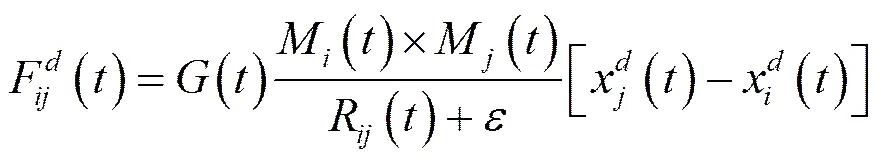
（5）

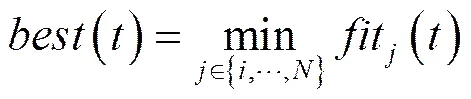
（8）

（10）

2.2 现代内点算法原理

H. Wei等人于2000年将现代内点算法应用于求解大规模水火最优潮流问题，取得了重要成果[5]。该算法考虑如式（1）描述的规划问题。先引入松驰变量对该问题进行等价变换：

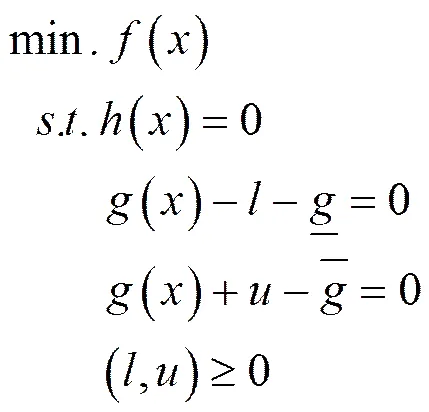
再构建一个拉格朗日函数。

（13）

得到KKT方程。

2.3 GSA-IPM混合算法

2.3.1 算法思路

以GSA算法为代表的随机方法，在处理离散问题上比较适合，但易陷入局部最优。以IPM为代表的确定性方法，虽在连续优化问题上有优势，但不适合处理离散变量。结合GSA与IPM的优点，提出一种GSA-IPM混合算法来求解无功优化。

首先采用GSA对离散变量进行初始化，计算其适应度。在潮流计算中用IPM对连续变量进行优化，优化结果再与GSA的结果交互迭代，再计算其适应度。对各个个体的目标函数值作排序，优秀个体替代次优个体参与下一轮迭代，直到找到最优解或迭代终止。

2.3.2 算法流程

GSA-IPM算法的流程见图1。

注：普通潮流网损(p.u.)为0.719

3 算例分析

为验证上述算法和模型的有效性，对某实际的船舶电力系统[2]进行仿真测试，所有数据都采用标幺值，电压约束是[1, 1.1]，无功出力约束是[-50, 50]。计算机配置条件为：Intel i5 CPU 4.21 GHz，4 GB内存，Windows 7 Professional，Matlab R2012a。

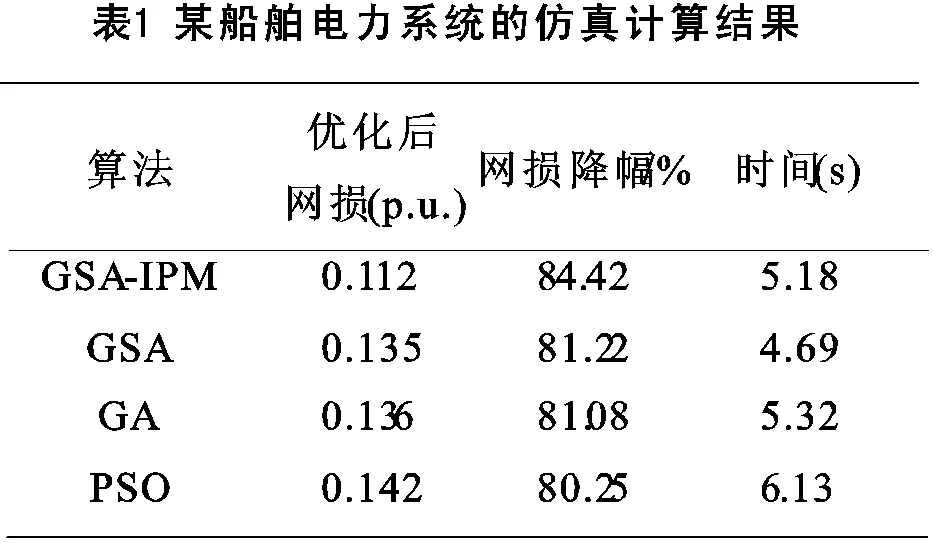
为了验证提出的GSA-IPM算法在求解船舶电力系统无功优化问题上的效果，分别利用GSA-IPM、GSA、GA和PSO这4种算法在相同条件下求解，其结果如表1所示。

由表1可见，万有引力算法能将该船舶电力系统的有功损耗优化得更低，由于采用了GSA与IPM的混合优化方法，其计算时间略长于单纯使用GSA算法。表2给出了初始潮流及GSA-IPM优化结果，所有电压都得到优化。

4 结论

1）提出的GSA-IPM算法适用于求解多目标、多变量、多约束的混合非线性规划问题。

2）通过对某实际船舶电力系统进行仿真测试，结果验证了所提算法和模型的正确性、有效性。

3）GSA-IPM算法船舶电力系统无功优化运行方法能改善系统的安全经济运行水平，具有更为优越的效益。

[1] 李彦, 董龙龙, 雍建容, 等. 基于改进粒子群算法的舰船电力系统无功优化[J]. 中国航海, 2014, 37(4): 30-33, 39．

[2] 唐卓贞, 沈苏海, 薛斌. 基于现代内点法的船舶电力系统无功优化[J]. 中国航海, 2010，33(3)：36-38．

[3] Rashedi, E., Nezamabadi-pour, H., Saryazdi, S. GSA: a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232–2248.

[4] S. Duman Y. Sonmez U. Guvenc, et al. Optimal reactive power dispatch using a gravitational search algorithm [J]. IET Gener. Transm. Distrib., 2012, 6(6): 1044–1051.

[5] H. Wei, H. Sasaki, J. Kubokawa, et al. Large scale hydro-thermal optimal power flow problems based on interior point nonlinear programming[J]. IEEE Transactions On Power Systems, 2000, 15(1): 396-403.

GSA-IPM Algorithm of Reactive Power Optimization for Ship’s Power System

Tang Zhuozhen

( Nantong Shipping College, Nantong 226010, Jiangsu, China )

TM7

A

1003-4862（2017）03-0009-04

2016-09-15

唐卓贞（1984-），女，硕士，讲师。研究方向：船舶电力系统。