一种用于不平衡畸变电网数字锁相环算法

石 媛，张新民



一种用于不平衡畸变电网数字锁相环算法

石 媛，张新民

(武汉船用电力推进装置研究所，武汉 430064）

为提高并网逆变器及整流器在不平衡及畸变电网下的控制性能，本文提出了一种基于Clarke变换理论及频率自适应的锁相环算法，该算法可同时应用于三相不平衡系统及单相系统。文中设计了用于提取不平衡电网中正序分量的滤波器，能够准确快速的识别不平衡电网的正负序分量。通过仿真分析可知，该锁相环算法对带直流分量的不平衡电网，电压瞬态变化具有良好的适应性。

锁相环 不平衡电网 直流分量

0 引言

在诸多电力电子设备，并网风力发电设备、可控整流器、UPS、动态电压恢复器等接入电网时，都存在电压突变（暂降或突升）、谐波以及由其他电力电子设备接入时引起的电压畸变等问题。为获得良好的控制性能，需要准确的获取电网的电压及相位信息，锁相环尤其是数字锁相环是应用最广泛及最有效的方式。

当电网电压平衡时，基于同步坐标系的SRF-PLL能够满足应用的需要，但这需要品质良好的电源[1]。国内外学者就不平衡电网下的锁相环设计提出许多解决策略。V.Kaura,V.Blasko应用了基于DQ变换理论的方法，但其锁相环的带宽及锁相时间都不太理想[2].文献[3]提出了对文献[2]进行了改进，在锁相环中加入负序、谐波分量滤波，并进行了相位补偿，在动态性能上取得良好效果。

为了使锁相环在不平衡电网下的应用更加简易，本文在阐述锁相环原理的基础上，建立了分离电网中正负序及直流分量的滤波器频域及时域模型，在MATLAB/SIMULINK环境中对电网各种畸变情况进行了锁相环的仿真。

1 锁相原理

在三相三线制系统中，忽略零序分量，当电网电压含有直流分量时，三相不平衡电网电压可表示为三相正序分量、负序分量、直流分量之和。对单相系统来说，可以看成是其它两相电压为0的三相不平衡系统。

式(1)中：+、-分别为正、负序分量的幅值；adc、bdc和cdc分别为abc三相电压所含的直流分量；为负序分量的相位；0为电网角频率。

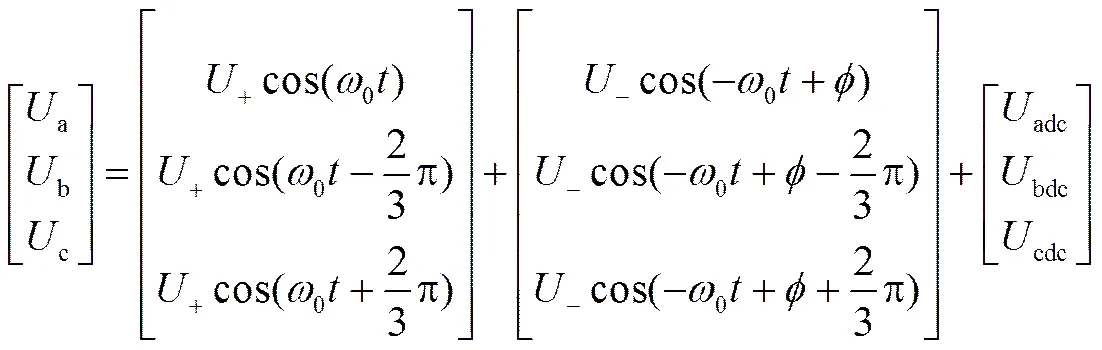
(2)

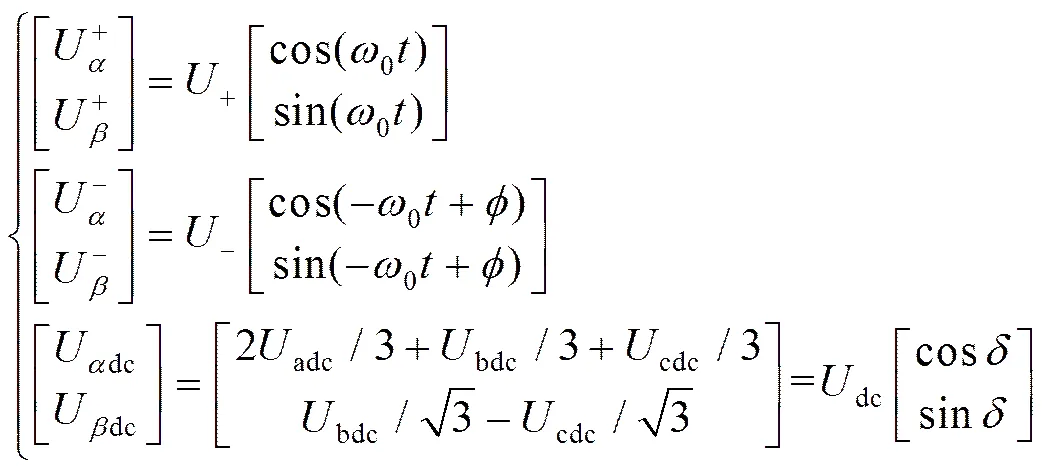
式(3)中dc和分别为直流分量在坐标系下形成向量的幅值和角度。从上式可以看出，三相电网电压的正序分量在坐标系下正序分量的角频率为0，而负序分量的角频率为-0，直流分量仍然为直流分量。因此，在闭环锁相前需要分解出电网电压的正序、负序和直流分量。提出的锁相环框图如图1所示。

图1 锁相环框图

电网电压正序和负序分量频率绝对值均为0，但极性相反(正序频率为0，负序频率为-0)。若要将电网电压中的正序分量滤出，所需滤波器必须满足频率0处幅频特性为1、相频特性为0，同时在其他频率处呈衰减趋势。直流分量可以看成频率为0 Hz的信号。综合考虑，建立滤波器频域数学模型如下：

课堂内的探究活动，受时间和空间的限制，一般不可能是完整的探究过程，即不可能包含完整的探究要素。因此，课堂内的探究活动过程，必然应该有所侧重，要制定明确的探究目标，作为实现探究活动的指向。

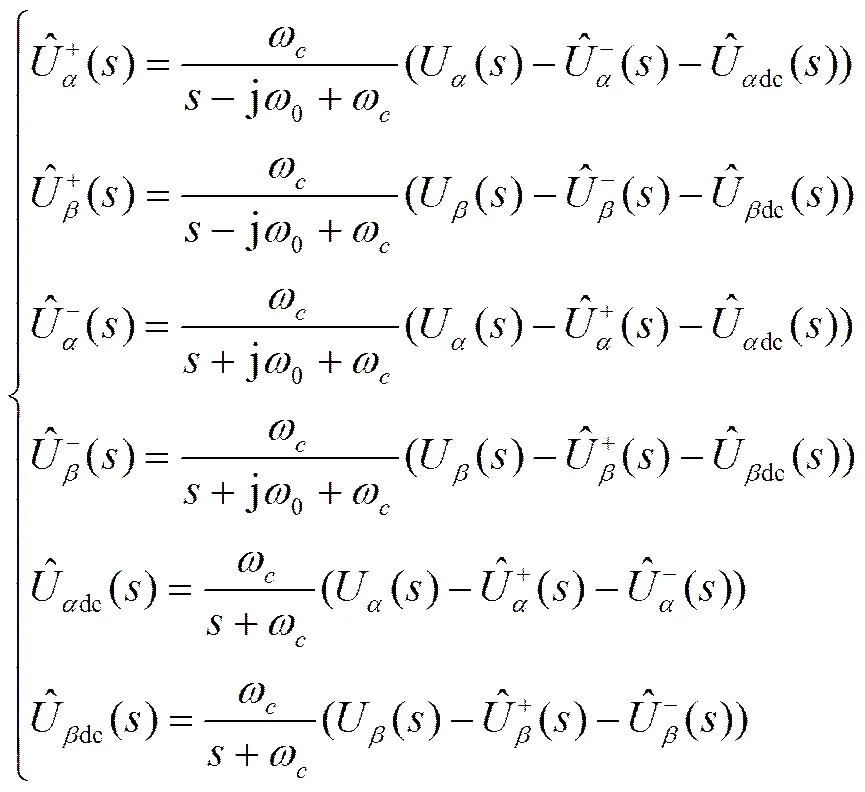
根据上式的频域数学模型可以得到滤波器时域数学模型：

(5)

式中c影响滤波器的带宽。滤波器动态响应主要取决于参数c，综合考虑滤波效果和动态性能，选择c=314。正负序解耦实现如图2所示。

当锁相环数字化实现时，特别是计算频率小于5 kHz时，需要补偿延时带来的误差，否则正序、负序和直流分量无法完全解耦滤波。

设锁相环计算周期为s，通过上一次估计值预测出下一次参与计算的估计值，预测公式如下

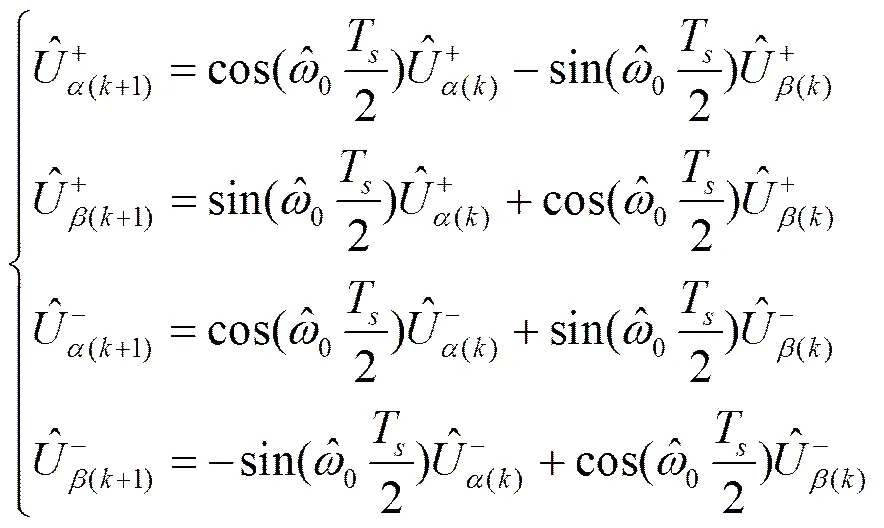
图2 正负序解耦

若锁相环在单相系统使用，单相可以看作是三相不平衡的一个特例，即三相中一相供电、两相断电的情况。

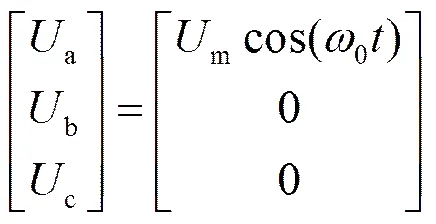
经Clarke变换后

(8)

2 仿真分析

对锁相环的仿真在Matlab/Simulink环境中进行，三相电网相电压除基波外分别加入直流偏置、特定谐波次数的电压（主要以35和37次谐波为主），仿真时电网电压波形如图3所示。经带宽417 Hz低通滤波后电网电压如图4所示。

2.1 某相电压突变

在这种工况下，模拟C相电压突然增大为额定值1.5倍时锁相环的调节能力。仿真结果如图5所示。非常清楚的看到，锁相环的相位非常稳定，没有发生大的变化，具有快速的锁相能力。

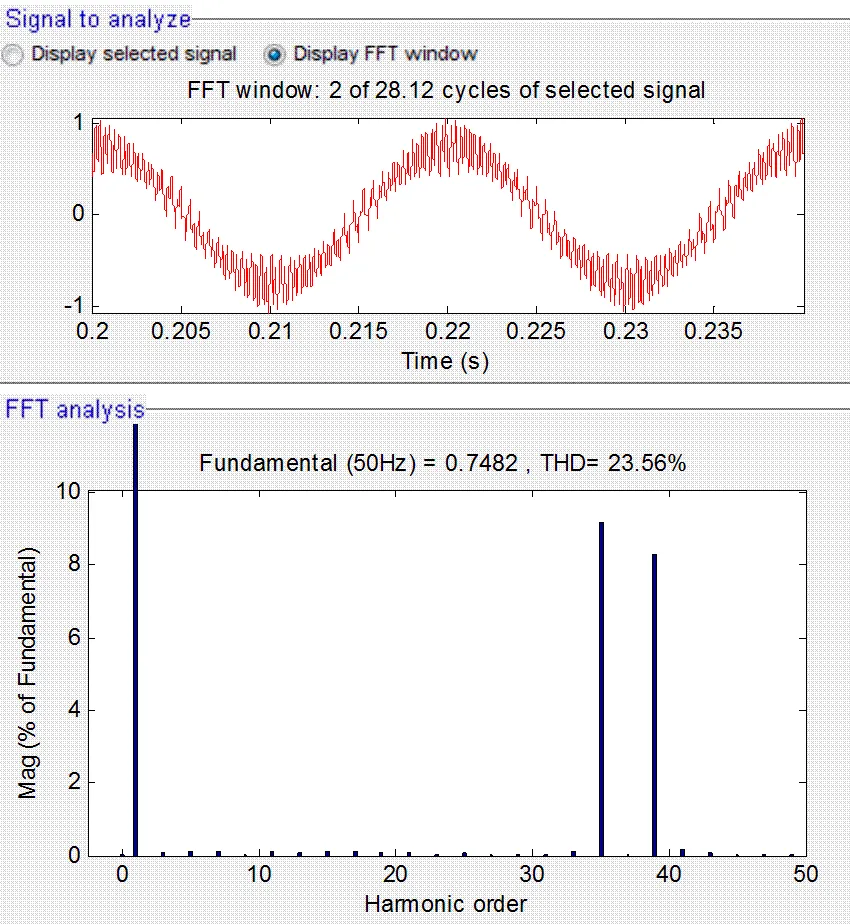
图3 电网电压FFT

图4 带宽417 Hz低通滤波后电网电压

图5 C相电压突增为1.5倍时动态调节过程

2.2 单相电压带直流偏置

模拟单相电压带直流偏置，仿真中在A相电压中加入一定的直流偏置，锁相环的输出波形如图6所示。由仿真波形可见，锁相环的相位在动态调节过程中非常稳定，锁相环响应速度快。

图6 A相电压直流偏置时动态调节过程

2.3 某相电压频率突变

仿真中将某相电压频率由50 Hz突变为51 Hz，经过锁相环调节后的锁相角度、锁相角频率如图7所示。仿真结果表明，锁相环对频率突变具有良好的适应性。

图7 频率突变为51 Hz时动态调节过程

2.4 应用于单相系统

该锁相环应用于单相系统的仿真如图8所示，仿真中将其它两相电压设置为0，由仿真结果得出，该锁相环对于单相系统的锁相也同样适用。

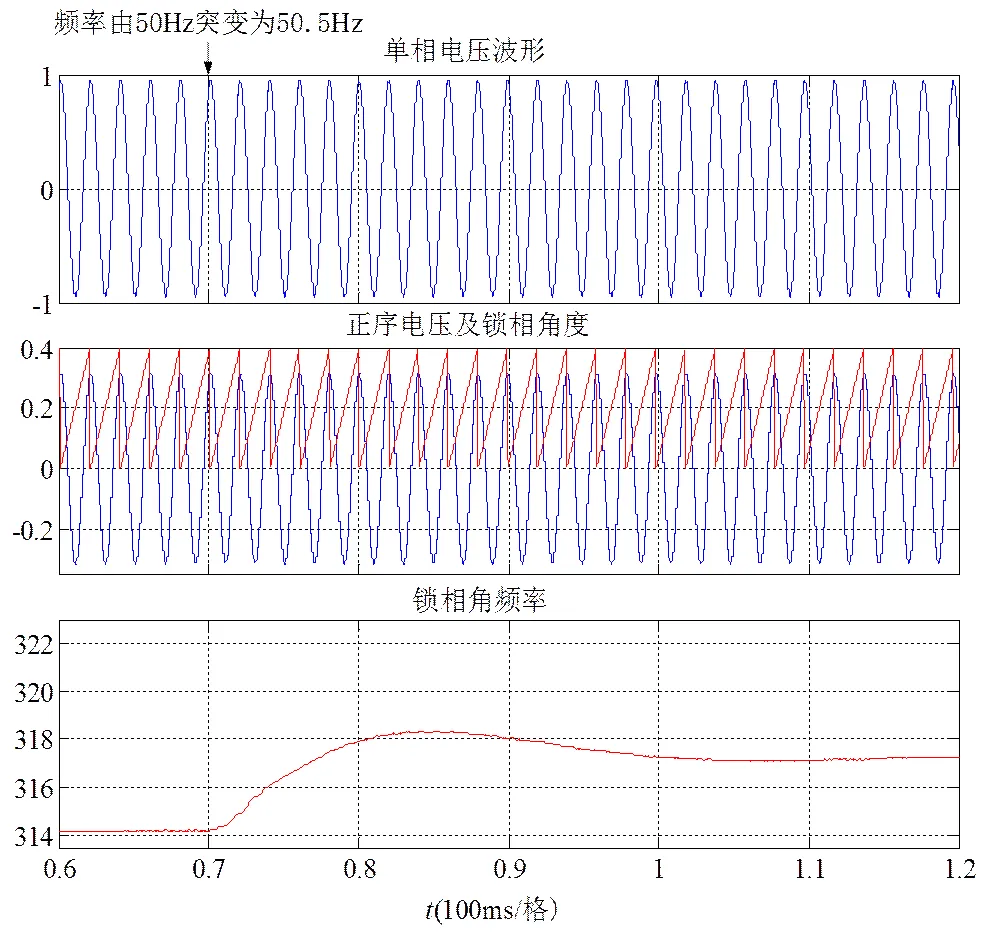
图8 单相系统锁相环动态调节过程

3 结语

本文在建立了一种基于Clarke变换理论及频率自适应的锁相环算法，通过设计合理的滤波器，对电网中的正、负序分量进行解耦。仿真结果表明了本文提出的锁相环对电网幅值阶跃跳变、频率突变、直流偏置及单相电源系统具有良好的适应性，锁相环动态响应迅速，相位稳定，验证了本文提出的锁相环的设计正确性。

[1] 王宝归, 李泽泉等. 并网型电力电子装置锁相环研究[J]. 大功率变流技术, 2012(4): 39-42.

[2] V. Kaura, V. Blasko, Operation of a phase locked loop system under distorted utility conditions, IEEE Trans. on Ind. Application, Vol.33, No.1 Jan/Feb 1997.

[3] Rakesh Kumar Sinha, Partha Sarathi Sensarma. Improved PLL under distorted utility conditions. IEEE International Conference on Industrial Technology, 2006: 1849 - 1854.

A Phase Locked Loop Algorithm Under Unbalanced and Distorted Grid Conditions

Shi Yuan, Zhang Xinmin

(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)

TM46

A

1003-4862（2017）06-0077-04

2017-03-15

石媛（1985-），女，工程师。研究方向：电力电子。E-mail: 315198341@qq.com