电弧仿真收敛性研究
2017-10-13吴国林张怀亮
吴国林,张怀亮
电弧仿真收敛性研究
吴国林1,张怀亮2
(1. 中国人民解放军91003部队,海南三亚572000; 2. 海军装备部装备采购中心,北京170001)
电弧仿真的研究,对于电器开关的发展改进有着重要意义。本文以稳态空气电弧为研究对象,对其中心轴附近近极区域建立了二维轴对称模型,利用MATLAB软件编程,采用局部细化网格的电弧仿真方法,对电弧近极的电位场进行了仿真,给出了一种解决电弧仿真过程中发散问题的新思路。
电弧仿真 收敛性 MATLAB
0 引言
随着电网中故障短路电流水平的不断提高[1-3],大容量分断设备的应用也越来越广泛。分断设备在分断短路电流时,会在分断的通流柱体之间产生电弧[4],大容量分段设备的广泛应用也使得电弧的研究越来越重要。电弧近极区温度的剧变使得近极区电弧物性参数变化剧烈,对该区域进行仿真时,若采用常规的网格划分方法,则极易使得计算发散。目前为避免发散问题的出现,大都将整个模型或该区域的网格划分得十分密集[5-7],使得电弧的仿真计算动辄数十小时,造成很大的资源浪费。
本文以稳态空气电弧为研究对象,对其中心轴附近近极区域建立了二维轴对称模型,利用MATLAB软件编程,给出了一种局部细化网格的方法,使得仿真计算大幅简化。
1 模型建立
1.1 物理模型
如图1所示,给出了电弧模型示意图,电弧为阳极与阴极之间的虚线部分,目前普遍将电弧作为圆柱体仿真。本文为简化模型,将电弧转化为二维模型,又由于本章的目的主要是解决电弧近极部分由于物性参数剧变带来的发散问题,从而仅取电弧中心轴附近区域进行仿真,即图1中斜线区域,并且仿真区域轴向长度为电弧轴向长度1/2。如图2所示,给出近极电弧模型的尺寸及边界条件,由于模型选取自电弧中心轴处,可认为电弧模型与电弧其他部分没有热量交换,模型热量只能由电极传出。
1.2 数学模型
1.2.1 电场方程
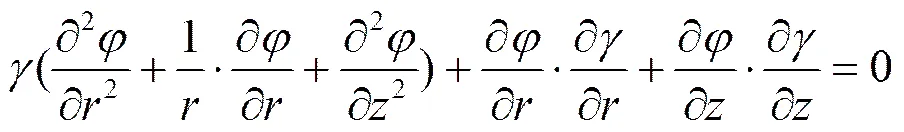
式(1)中,及分别为圆柱坐标径向及轴向分量;表示电位,单位;表示电导率,单位1/s。
图1 电弧模型示意图
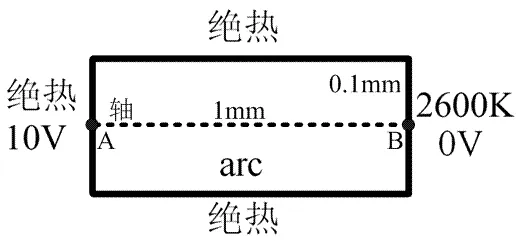
图2 模型边界
1.2.2 导热微分方程
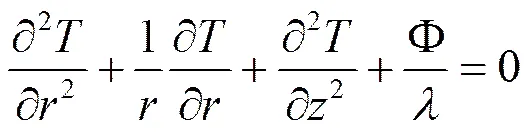
式(2)中,表示温度,单位为K;表示单位体积单位时间内产生的热量,单位J;表示热导率,单位W/m•K[8]。
1.3 离散方法
本文采用有限差分法对所建立的数学模型进行离散。首先对仿真区域进行网格划分。用(i,j)表示点(i,j)的温度,用(i,j)表示点(i,j)的电位,如图3所示。

图3 网格剖分
进行网格划分后,任一内部节点(i,j)在方向上的偏导可以由其四周的点之间的关系进行描述,从而得到内部节点(i,j)的离散公式(以电位的离散公式为例):
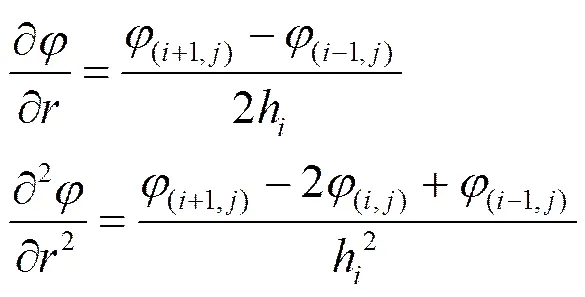
2 收敛条件
由文献[9-11]可知,对于式(3)所示线性方程组,若系数矩阵中的每一行中不在主对角线上的所有元素的绝对值之和小于同一行中主对角线元素之绝对值,即:
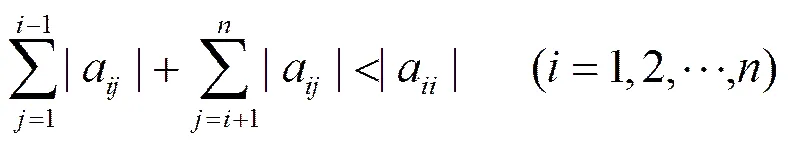
则称(3)为系数矩阵按行严格对角占优,并且对于该方程组,简单迭代法及Seidel迭代法都收敛。
(3)
3 MATLAB程序设计
3.1 MATLAB程序设计
如图4及图5所示,给出了近极电弧仿真计算的MATLAB程序框图,包括主程序及子程序两部分,主程序实现大网格划分模型的仿真计算,并实现对各网格节点收敛性的实时监测。一旦发现不满足严格对角占优的点,即调用子程序,将该点坐标输入给子程序,子程序将不稳定点处以密集网格划分,并以迭代法求解不稳定点的温度值及电位值,并将计算结果返回给主程序,主程序再进行后续的迭代计算。
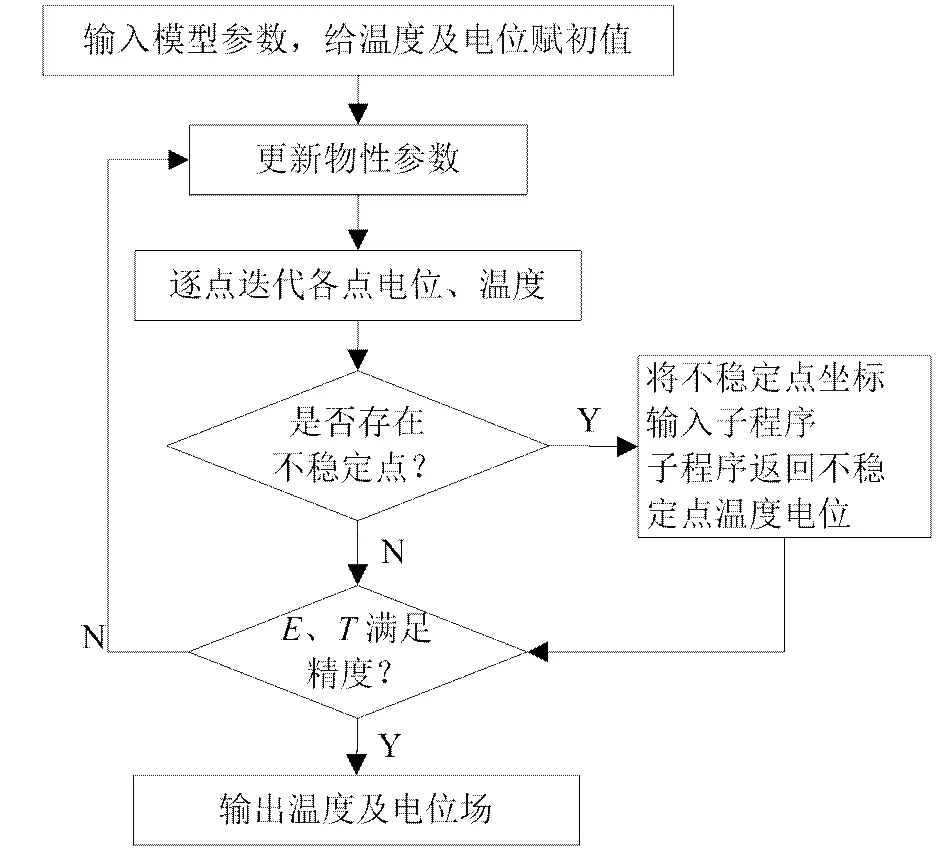
图4 主程序
3.2 局部密集网格划分方法
如图6所示,为局部密集网格细化方法示意图,下面以电位的处理为例,介绍实现方法。当主程序以迭代法解方程组时,检测到点(0,0)不满足按行严格对角占优时,即调用子程序,并将1,,3,12,3输入给子程序。若子程序中将网格尺寸大小变为原来的1/n,则a, b, c, d四点电位分别为(以n=3为例):

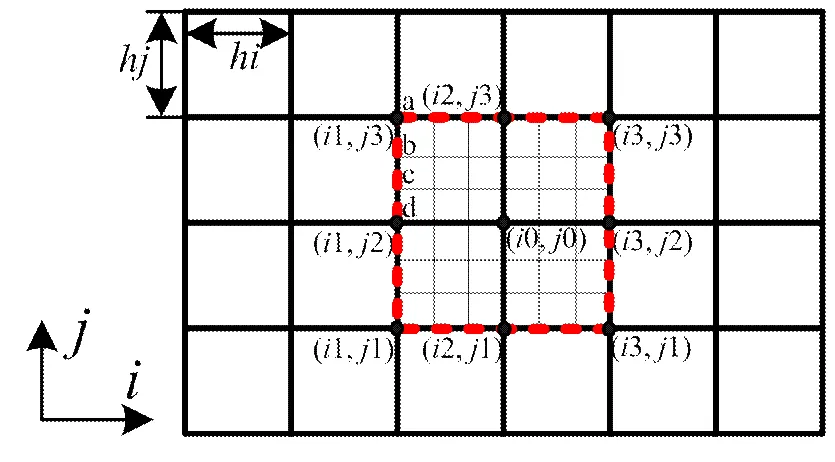
图6 局部网格细化
同理,红色虚线框上其他点的电位均以此方法给出,红色虚线框上点的电位值实际上相当于局部小网格区域的第一类边界条件。红色虚线框内部点的电位值也以这种方法给出,这就相当于给所有点赋初值。局部小网格区域实际上相当于一个新的模型,满足电位微分方程及导热微分方程,其边界条件均为第一类边界条件,同样用迭代法求解该方程组,可得点()的电位值及温度值,子程序将点()的电位值及温度值返回给主程序,主程序即得到了满足按行严格对角占优求解得到的收敛值。
4 近极电弧仿真结果
如图7所示,给出了模型电位的轴向分布,即图2中电弧模型轴AB上的电位分布。仿真中将电弧在轴向上划分为101个大网格,网格0对应电弧的中心点A,网格101对应于点B。图7中,纵轴表示电位值,横轴表示网格。由电位分布可以看出,近极电弧远离触头表面的大部分区域的电位梯度都很小,而在靠近触头表面的小距离内发生了巨大的跃升。

图7 电位分布
文献[12]中给出了普遍认为的电弧电位的轴向分布,如图8所示。电弧由三部分组成:阴极区、阳极区以及等离子区。阴极区紧邻阴极表面,并且厚度很小,但是大部分电弧电压都施加在这一个狭小的区域,这使得阴极区具有很高的电场强度。当电流足够大时,会在靠近阳极表面的位置出现阳极区,阳极区也分担一部分电弧电压。等离子区是位于阴极区和阳极区之间的广大区域,等离子区中充满着等离子体,等离子区中的正、负粒子都具有很高的密度,使得等离子区的导电性非常好,从而等离子区电位梯度较小。
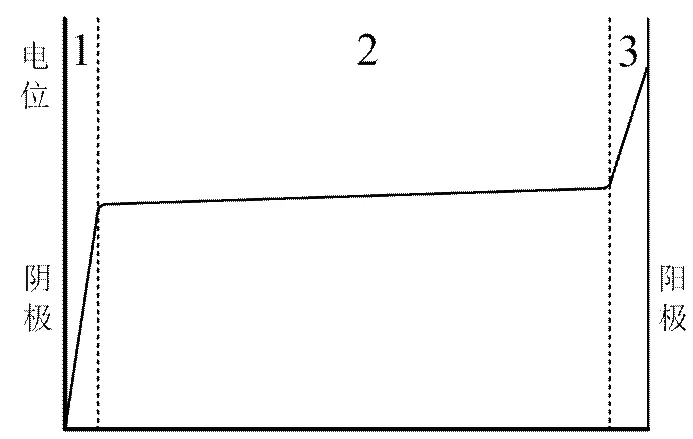
图8 电弧电位轴向分布
1-阴极区 2-等离子区 3-阳极区
5 结论
本文以MATLAB软件自编程,提出了一种仿真模型局部采用密集网格划分的方法,可以有效避免电弧仿真易发散问题,给出了一种电弧仿真的新思路。
[1] 袁志方, 庄劲武, 王晨, 等. 石英砂对于电磁斥力高速开断器介质恢复特性的影响[J].高电压技术, 2014, 40(1): 294-299.
[2] 陈博, 庄劲武, 肖翼洋, 等. 10KV/2KA混合型限流熔断器用电弧触发器的分析与设计[J]. 高电压技术, 2012, 38(8): 1948-1955.
[3] 袁志方, 庄劲武, 王晨, 等. 窄缝灭弧法提升电磁斥力高速开断器电弧电压的分析与试验[J]. 中国电机工程学报, 2013, 33(33): 139-144.
[4] 顾雪晨, 王晨. 直流电力系统短路限流装置研究[J]. 船舶, 2012, 23(3): 60-62.
[5] Alferov F, Nevrovskii A, Sidorov A. Anode mode of vacuum arc in multirod electrode system[J]. High Temperature, 2002, 40(1): 15-20.
[6] Wang L, Jia S, Yang D, et al. Modeling and simulation of anode activity in high-current vacuum Arc[J]. Phys. D: Appl. Phys., 2009, 42(5): 62-67.
[7] 王立军, 贾申利, 刘宇, 等. 纵磁下真空电弧阳极热过程的仿真[J]. 中国电机工程学报, 2011, 26(3): 66-72.
[8] 戴锅生.传热学(第二版)[M]. 北京: 高等教育出版社, 2011: 22-25.
[9] 何汉林, 梅家斌. 数值分析[M]. 北京: 科学出版社, 2007: 79-82.
[10] 何汉林, 魏汝祥, 李卫军. 数值分析[M]. 武汉: 湖北科学技术出版社, 1999.
[11] 罗家洪, 方卫东. 矩阵分析引论[M]. 广州: 华南理工大学出版社, 2006.
[12] 王其平. 电器电弧理论[M]. 北京: 机械工业出版社, 1992.
Research on the Convergence of Arc Simulation
Wu Guolin1, Zhang Huailiang2
(1. Unit 91003 of PLA, Shanya 572000, Hainan, China; 2. Armaments Procurement Agency, Naval Equipment Ministry, Beijing 100071, China)
TM5 TP391.9
A
1003-4862(2017)06-0006-03
2017-03-13
吴国林(1990-),男,硕士。专业方向:电气工程。E-mail: wuguolin1990@163.com
