星型结多工器综合

王 瑞，李乐中，彭 龙，涂小强，钟小溪



星型结多工器综合

王 瑞，李乐中，彭 龙，涂小强，钟小溪

(成都信息工程大学光电技术学院 成都 610225)

提出了一种利用线性变换综合星型结多工器的方法。该方法基于线性变换综合出多工器的每个信道滤波器参数对应的特征多项式，利用文献中已有的技术综合出多工器的阶耦合矩阵。给出了多工器阶耦合矩阵的构造方法，并推导了多工器参数和群时延与阶耦合矩阵的关系。为了验证该方法，给出了一个五工器及一个双工器的综合实例，其中双工器被进一步设计、加工与测试，测试结果与综合结果相吻合，进一步验证了该方法的准确性。

耦合矩阵; 线性频率变换; 多工器; 星型结; 综合

谐振腔滤波器可作为独立器件[1-2]或多工器的一部分。多工器通过共用单根天线，用于多频率段通信的微波通信系统，它由多个信道滤波器构成，是微波系统的重要器件，通过谐振腔之间不同的耦合可实现滤波器及多工器的设计。由谐振腔之间的耦合系数构成一个阶的耦合矩阵(是谐振腔的个数)，根据多工器或滤波器的指标确定称为综合，文献[3]是滤波器综合的经典技术。而对于多工器，由于构成多工器的信道滤波器之间相互影响，每个信道滤波器不能根据指标直接使用经典技术[3]综合。为实现多工器综合，基于优化法[4-7]及分析法[8-9]近年被提出，优化法通常依赖于待优化参数初始值的选择。文献[8]提出了一种新型结构多工器，该结构通过一个公共谐振腔与每个信道滤波器的第一个谐振腔耦合，称为星型结多工器，并且基于多项式综合了该类多工器。文献[9]基于相位倒向器变换技术(phased-inverter to frequency-invariant reactance inverter transformation)综合了星型结多工器。在国内，未见有报道此类多工器的综合与设计。本文提出一种线性频率变换，并利用已有的技术[3,8]综合星型结多工器，并给出整个多工器的耦合矩阵构造方法，推导多工器的参数及群时延与耦合矩阵之间的关系。根据指标综合出的耦合矩阵可作为星型结多工器设计的依据，如三工器[10]。

1 多工器综合理论分析

1.1 基于线性频率变换计算多工器的多项式

图1a给出了本文要综合的星型结多工器的结构。第个信道滤波器的参数为：

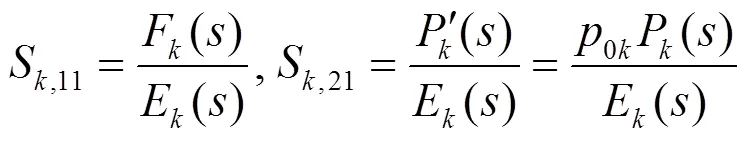
(1)

式中，是归一化的复频率域，与归一化频率域的关系为；、、的根分别代表第个信道滤波器的反射零点，传输零点及极点；为多工器信道的总个数。

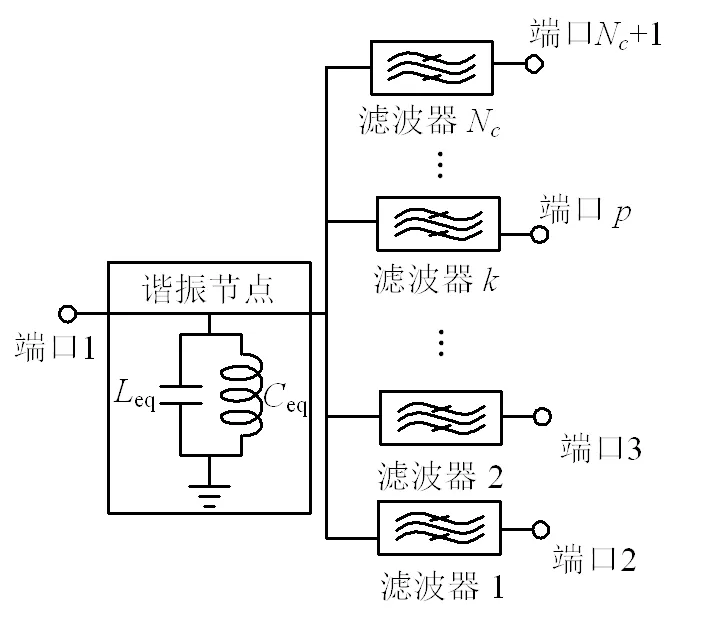
a. 星型结多工器结构

b.至的映射关系

c. 本文提出的至的映射关系

有N+1个端口多工器的参数可用多项式表示为：

(2)

式中，()、()的根分别代表多工器在端口1(作为输入端口)处的反射零点和极点，其阶数等于多工器谐振腔的总个数，最高阶的系数均为1；表示端口1与端口之间的传输多项式；、分别代表多项式、最高项的系数。

1.2 多工器阶耦合矩阵的构造

图2 综合多工器获得耦合矩阵M的过程图

本文的多工器的综合过程为：1) 利用1.1节中提出的方法，获得式(1)中每个信道滤波器初始的多项式。2) 利用文献[8]中的迭代获得式(2)中多工器的多项式。3) 进一步获得式(1)中每个信道滤波器的多项式，此时获得式(1)中的多项式已考虑多工器中各个信道滤波器的相互影响。4) 利用过程3)中获得的信道滤波器多项式，根据文献[3]中的技术获得第个信道滤波器的阶耦合矩阵，记为。5) 由过程4)获得的构造出整个多工器的耦合矩阵。在Matlab程序中获得及各端口处归一化阻抗的主要过程如图2所示。

是归一化的耦合矩阵，为实现多工器的设计必须利用下式对去归一化：

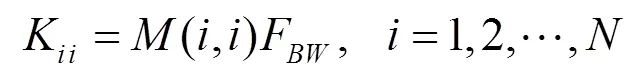
1.3 基于阶耦合矩阵计算多工器的参数及群时延

多工器的参数使用阶的耦合矩阵用下式计算：

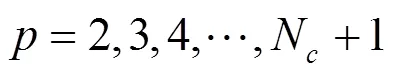
式(5)的推导综合参考了文献[5,11-12]。端口1位于谐振腔编号1的位置；端口位于谐振腔编号的位置；端口位于谐振腔编号的位置，如图3b中，若计算23,，则=2，=3，=6，=13；若计算31，则=3，=1，=13，=1。、分别是端口和端口处的归一化阻抗。

参考滤波器群时延归一化域的定义[12]，推导出在实际频率域多工器群时延的计算为：

2 综合与设计实例

2.1 星型结五工器的综合

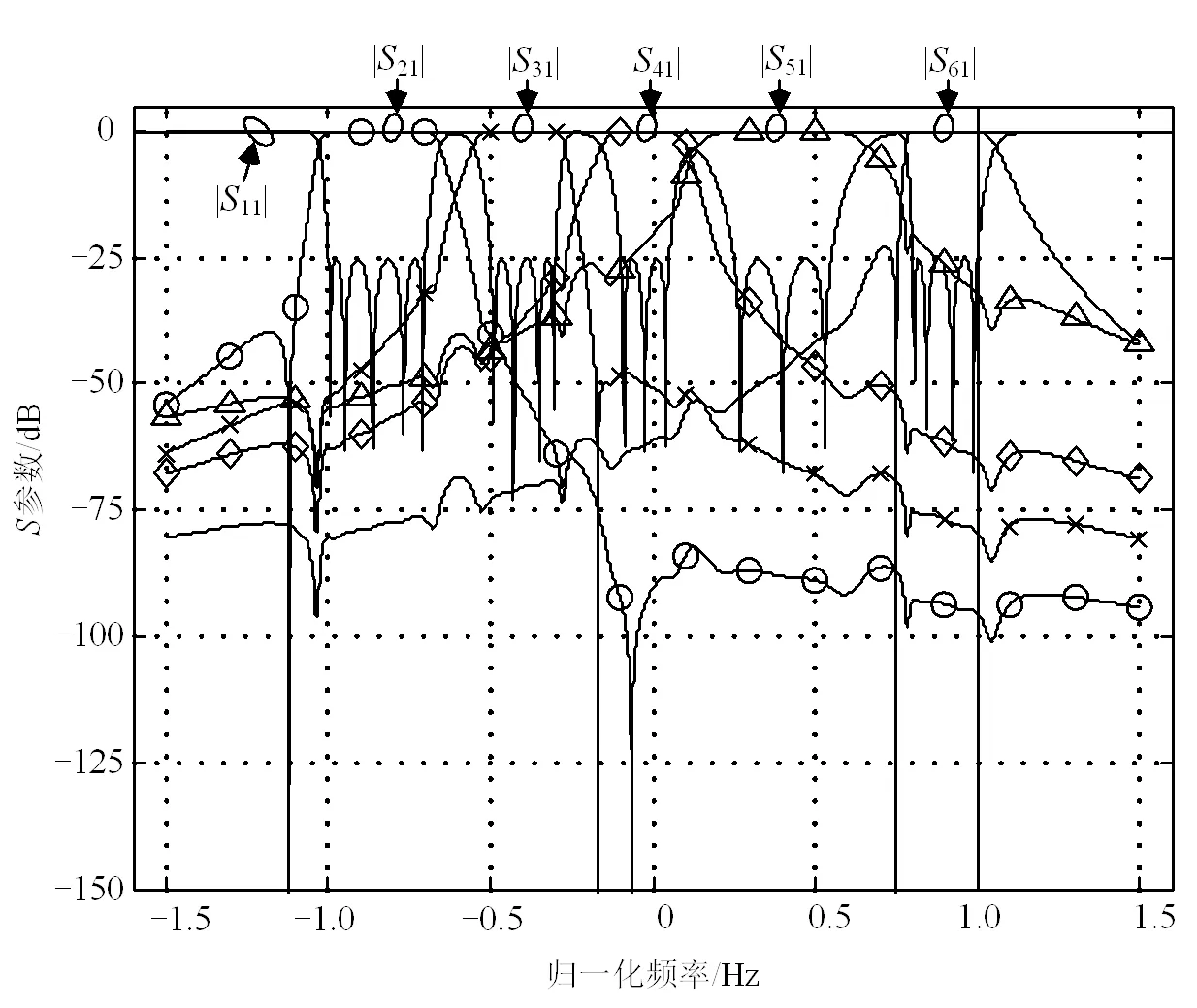
a. 综合的五工器频率响应

b. 五工器的耦合结构

图3 综合的五工器频率响应及耦合拓扑结构

利用提出的方法，综合出的五工器频率响应及耦合结构如图3所示。图3a给出了利用综合出的耦合矩阵计算的归一化频率域域中的参数，图3b给出了该五工器可实现的一个耦合结构。谐振腔之间的耦合系数已标注在图3b上。

每个谐振腔的自耦合系数M=[0 0.875 9 0.931 6 0.842 7 0.818 7 0.846 3 0.403 7 0.409 3 0.356 2 0.405 0 0.032 6 0.026 7 0.025 5-0.409 9-0.403 1-0.400 8-0.935 2-0.918 6-0.829 5-0.909 1]，。各端口处的归一化阻抗值R=[2.284 9 0.188 2 0.132 6 0.110 8 0.221 7 0.131 6]，。从图3a可以看出，综合的参数完全满足指标要求，验证了本文方法的有效性。

2.2 星型结双工器的综合与设计

通带(GHz)：(2.4～2.453)，(2.543～2.6)；即=2.4，=2.453，=2.543，=2.6。双工器阶数=7；信道滤波器阶数：[3,3]；信道滤波器回波损耗(dB)：[20,0]；每个信道滤波器均是全极点滤波器。

根据以上指标要求，利用本文提出的方法综合出去归一化的耦合系数：=0.061 9，=0.020 7，=0.022 7，=0.062 4，=0.021 0，=0.023 0；端口处谐振腔的外部品质因子：=5.78，=38.18，=37.60；每个腔的中心频率(GHz）：=[2.498 0 2.430 2 2.427 1 2.426 9 2.567 2 2.570 5 2.570 7]，。

双工器的设计选择使用Rogers 5880介质基片，相对介电常数为2.2，厚度为0.508 mm，其耦合拓扑结构如图4a所示，基片上金属导体结构层如图4b所示。使用文献[11]介绍的方法，利用电磁仿真软件IE3D，根据以上获得的去归一化的参数确定双工器的初始尺寸，可进一步利用滤波器的调试方法[13-14]调试每个信道滤波器，最终获得的双工器尺寸如图4b所示。

a. 耦合拓扑结构

b. 物理结构及尺寸

图4 设计7阶双工器的拓扑结构及物理尺寸

图5给出了IE3D仿真的参数及群时延与测试的参数及群时延的对比，二者有较好的一致性，实际测试的结果与仿真相比中心频率向低频率端漂移了约50 MHz，这主要是实际基片相对介电常数的变化导致的。仿真及测试的结果进一步验证了本文提出的星型结多工器的综合方法及推导的多工器参数和群时延的计算式的正确性。

a. 测试与仿真的参数

b. 测试与仿真的群时延

图5 设计7阶双工器的参数及群时延星型结双工器域的指标如下

3 结束语

本文利用提出的线性变换与文献中已有的技术，综合了一类星型结多工器，这类多工器的特点是通过一个公共的谐振腔作为谐振节点，与每个信道滤波器的第一个谐振腔相连。进一步给出了该类多工器阶耦合矩阵的构造方法，并推导了基于耦合矩阵计算多工器的参数和群时延。利用本文提出的方法，综合了一个五工器和一个双工器的实例，其中综合的双工器被进一步设计、加工与测试，该双工器的通带工作在2.4～2.453 GHz和2.543～2.6 GHz，利用7个开口环谐振腔实现，设计使用了相对介电常数为2.2，厚度为0.508 mm的罗捷斯5880介质基片，IE3D仿真的结果与矢量网络分析仪测试的结果满足指标的要求。本文提出的多工器综合方法综合出的多工器耦合矩阵计算的参数完全满足设计指标的要求，从而验证了提出的基于线性频率变换技术综合星型结多工器方法的有效性。

[1] 胡皓全, 曹纪纲. 新型微带交叉耦合环微波带通滤波器[J]. 电子科技大学学报, 2008, 37(6): 875-880.

HU Hao-quan, CAO Ji-gang.Novel microwave bandpass filter with microtrip cross-coupled square open-loop resonators[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(6): 875-880.

[2] 孙守家, 吴边, 梁昌洪. 新型双模方环微带带通滤波器 [J]. 西安电子科技大学学报, 2014, 41(1): 53-56.

SUN Shou-jia, WU Bian, LIANG Chang-hong. Novel dual-mode square loop microstrip bandpass filter[J]. Journal of Xidian University, 2014, 41(1): 53-56.

[3] CAMERON R J. Advanced coupling matrix synthesis techniques for microwave filters[J]. IEEE Trans on Microwave Theory and Techniques, 2003, 51(1): 1-10.

[4] SKAIK T F, LANCASTER M J, HUANG F. Synthesis of multiple output coupled resonator circuits using coupling matrix optimization[J]. IET Microw Antennas Propag, 2011, 5(9): 1081-1088.

[5] SKAIK T F, LANCASTER M J. Coupled resonator diplexer without external junctions[J]. Journal of Electromagnetic Analysis and Applications, 2011, 3(6): 238-241.

[6] SKAIK T. Novel star-junction coupled-resonator multiplexer structures[J]. Progress in Electromagnetics Research Letters, 2012, 31: 113-120.

[7] SHANG Xiao-bang, WANG Yi, XIA Wen-lin, et al. Novel multiplexer topologies based on all-resonator structures[J]. IEEE Trans on Microwave Theory and Techniques, 2013, 61(11): 3838-3845.

[8] MACCHIARELLA G, TAMIAZZO S. Synthesis of star-junction multiplexers[J]. IEEE Trans on Microwave Theory and Techniques, 2010, 58(12): 3732-3741.

[9] ZHAO Ping, WU Ke-li. An iterative and analytical approach to optimal synthesis of a multiplexer with a star-junction[J]. IEEE Trans on Microwave Theory and Techniques, 2014, 62(12): 3362-3369.

[10] TANG C W, CHEN M G. Packaged microstrip triplexer with star-junction topology[J]. Electronics Letters, 2012, 48(12): 699-701.

[11] HONG Jia-sheng, LANCASTER M J. Microstrip filters for RF/microwave applications[M]. New York: Wiley, 2001.

[12] AMARI S. Synthesis of cross-coupled resonator filters using an analytical gradient-based optimization technique[J]. IEEE Trans on Microwave Theory and Techniques, 2000, 48(9): 1559-1564.

[13] WANG Rui, PENG Long, LI Le-zhong. Diagnosis of lossy resonator filters with source–load coupling using Y-parameters[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2014, 24(6): 713-717.

[14] WANG Rui, PENG Long, LI Le-zhong. Improved diagnosis of lossy resonator bandpass filters using Y-parameters[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2015, 25(9): 807-814.

编 辑 漆 蓉

Synthesis of Star-Junction Multiplexers

WANG Rui, LI Le-zhong, PENG Long, TU Xiao-qiang, and ZHONG Xiao-xi

(College of Optoelectronic Technology, Chengdu University of Information Technology Chengdu 610225)

This paper presents a method for synthesizing coupled resonator multiplexers with a star-junction (an extra resonant junction in addition to the channel filters). A linear frequency transformation is proposed for the evaluation of the characteristic polynomials of the each channel filter composed of star-junction multiplexers, and then coupling matrix of overall multiplexers can be obtained by using the proposed linear frequency transformation and well-established method. The evaluation of group delay in the physical frequencydomain and-parameters based on coupling matrix are derived. To illustrate the validation of the method, two examples, including 25-poles multiplexers and 7-poles diplexer, have been synthesized, and the 7-poles diplexer has been further designed, manufactured and measured. The measured resuts are in good agreement with the synthetic results, which further verify the accuracy of the proposed method.

coupling matrix; linear frequency transformation; multiplexers; star-junction; synthesis

TN713

A

10.3969/j.issn.1001-0548.2017.04.008

2016-05-05；

2016-12-25

国家自然科学基金(51502025)

王瑞(1980-)，男，博士，主要从事微波及毫米波电路、太赫兹技术方面的研究.