基于峭度和时域能量的局放脉冲提取算法

张安安，何 聪，孙茂一，李 茜



基于峭度和时域能量的局放脉冲提取算法

张安安1，何 聪1，孙茂一2，李 茜1

(1. 西南石油大学电气信息学院 成都 610500；2. 中国测试技术研究院流量所 成都 610021)

提出了一种针对电力电缆局部放电脉冲的提取方法，首先根据信号峭度的变化定位局部放电脉冲峰值所在位置，然后根据信号能量的变化采用滑动能量搜索的方法以局部放电脉冲峰值为中心向两边计算搜索局放脉冲的边沿，从背景噪声中准确提取局放脉冲信号。该方法可以将局部放电检测信号中纯噪声信号部分与包含局部放电脉冲信号的部分区分开来，且不受局部放电脉冲个数和脉冲所在位置的限制，并具有步骤简洁、计算量小的特点。通过与小波阈值去噪、经验模态分解(EMD)两种主流电力电缆局部放电脉冲提取方法的仿真实验对比和实际实验对比，验证了该方法的有效性与准确性。

峭度; 局部放电; 局部放电脉冲提取; 时域滑动能量

电力电缆局部放电检测是电力电缆绝缘性能评估的常用方法之一[1-2]。但是，由于背景噪声的存在，电力电缆局部放电在线检测所采集的信号含有大量的噪声，使单个局放脉冲信号的边沿变的很不明显，给后期的局部放电脉冲信号特性分析、识别带来了一定的困难。因此，确定局部放电脉冲信号的边沿，准确地从背景噪声中提取局部放电脉冲波形已成为电力电缆局部放电检测技术关键问题之一。

局部放电脉冲信号的提取作为局部放电测量信号预处理阶段的关键步骤，是局部放电信号深入分析的基础。目前有很多分析处理局部放电信号的方法，如小波阈值去噪法、经验模态分解(empirical mode decomposition, EMD)[3]去噪法、傅里叶变换数字滤波法、自适应滤波法等，其中小波去噪法与EMD去噪法应用较为广泛。文献[4]提出了应用复小波变换对超高频局放信号进行去噪，但是复小波的选择、小波分解阶数的确定和阈值算法的选取较难同时达到最佳。文献[5]利用谱峭度[6]设计自适应带通Wiener滤波器滤波后再进行小波平滑去噪。但由于Wiener滤波器参数是固定的，要想实现最优的滤波效果必须对信号和噪声的统计特性有先验知识，但是在实际中，常常难以预知这些统计特性。文献[7]利用小波迹理论[8]抑制信号噪声，并通过循环平移方法强化消噪效果。小波迹建立在小波变换基础之上，通过有限基函数或基向量的集合表示任意信号，但并未充分考虑信号自身特性。文献[9]采用希尔伯特黄变换(Hilbert-Huangtransform, HHT)，先对信号进行EMD，再进行三维希尔伯特能量谱分析。但局部放电信号往往包含较多冲击成分，利用EMD处理局部放电这类间歇现象较为明显的信号时容易造成模态混叠。另外还有一些其他的方法，如文献[10]提出基于信号稀疏分解的局放信号去噪法，通过与所构建的过完备原子库进行匹配实现有用信号的分解重构。文献[11]对传统的FFT阈值置零滤波方法进行了改进来抑制窄带干扰，其主要思路是选取合适的压缩倍数，对窄带干扰所在的频带进行分块阈值压缩处理，并对周围的频带利用插值补偿或最小二乘法进行了加宽处理。文献[12]提出了分块阈值空域相关联合去噪法，该算法先用分块阈值去噪法对染噪信号小波分解的子带信号进行预处理，然后采用空域相关法进行数据处理，最后将处理结果重构回原信号。

本文提出了一种基于峭度准则和时域滑动能量搜索的电力电缆局部放电脉冲提取方法。该方法首先利用信号峭度的变化定位局部放电脉冲在数据窗中的位置，然后再利用信号时域能量的变化确定局部放电脉冲波形边沿。此外，该方法可以将局部放电测量信号中含有局部放电脉冲波形的部分与纯噪声部分区分开，提高了计算效率。

1 基本理论

1.1 峭度准则

峭度反映了振动信号分布特性的数值统计量，是归一化的四阶中心矩和描述波形尖峰度的一个无量纲参数[13]。对于长度为的信号，其峭度的数学表达式为：

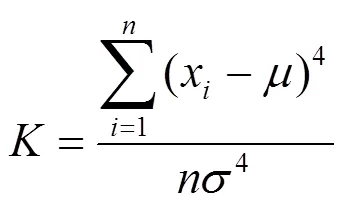
当信号近似服从正态分布时，其峭度值约为3，而当信号存在较多冲击成分时，峭度值明显增大，冲击越大峭度值也就越大[13]。

1.2 信号时域能量

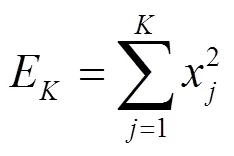
(3)

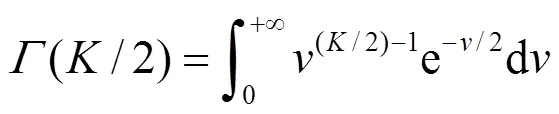
2 含噪局部放电信号特性分析

电力电缆局部放电测量信号中不仅含有局放脉冲信号，同时含有大量的噪声信号。局部放电信号的分析应该包含信号中所有成分的特性分析。

2.1 噪声特性分析

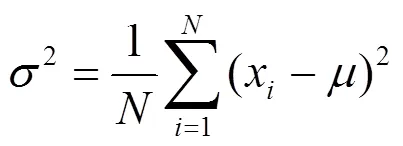
2.2 峭度特性分析

当电力电缆局部放电测量信号主要为背景噪声时，其信号的幅值分布接近于正态分布，因此其峭度值约等于3。当有局部放电现象发生时，由局部放电引起的脉冲信号明显偏离正态分布，使信号的峭度值增大。根据这一特性，本文通过信号峭度的变化来粗略定位局部放电脉冲所在的位置。

2.3 时域能量特性分析

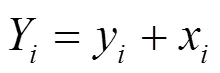
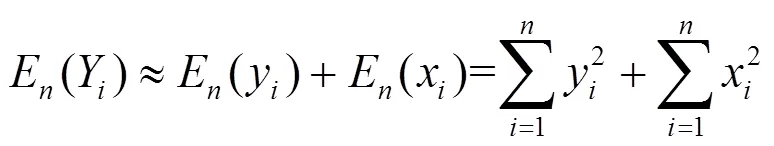
通常可将电力电缆局放检测背景噪声认为是服从正态分布的随机序列。则可看作服从自由度为的分布，记为，则其概率密度函数为：

(8)

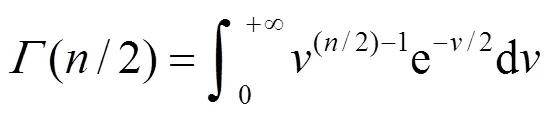
表1 计算结果

表1 计算结果

M 1025.19 2040.00 3053.67 4056.77 5079.49 6091.95 70104.20 80116.30 90129.30 100140.10

则：

(11)

由此可得，当取能量窗样本噪声序列点数为20时，其时域能量大于40的概率几乎为0，因此，本文选取时域能量宽度为20，能量阈值为40，定义如下：

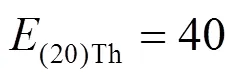
3 方法步骤

通过上述分析，基于峭度准则和时域滑动能量搜索的局部放电脉冲提取方法可以总结为以下3个步骤：

1) 数据窗长度取20计算信号峭度，峭度大于3，且增量明显处定为局部放电脉冲所在区域。

2) 取脉冲所在区域中心点，记为，以为中心采用滑动能量法向左向右搜索脉冲边沿。

3) 确定脉冲边沿，提取局部放电脉冲。

综上所述，本文提出的基于峭度准则和时域滑动能量搜索的局部放电脉冲提取方法的主要流程如图1所示。

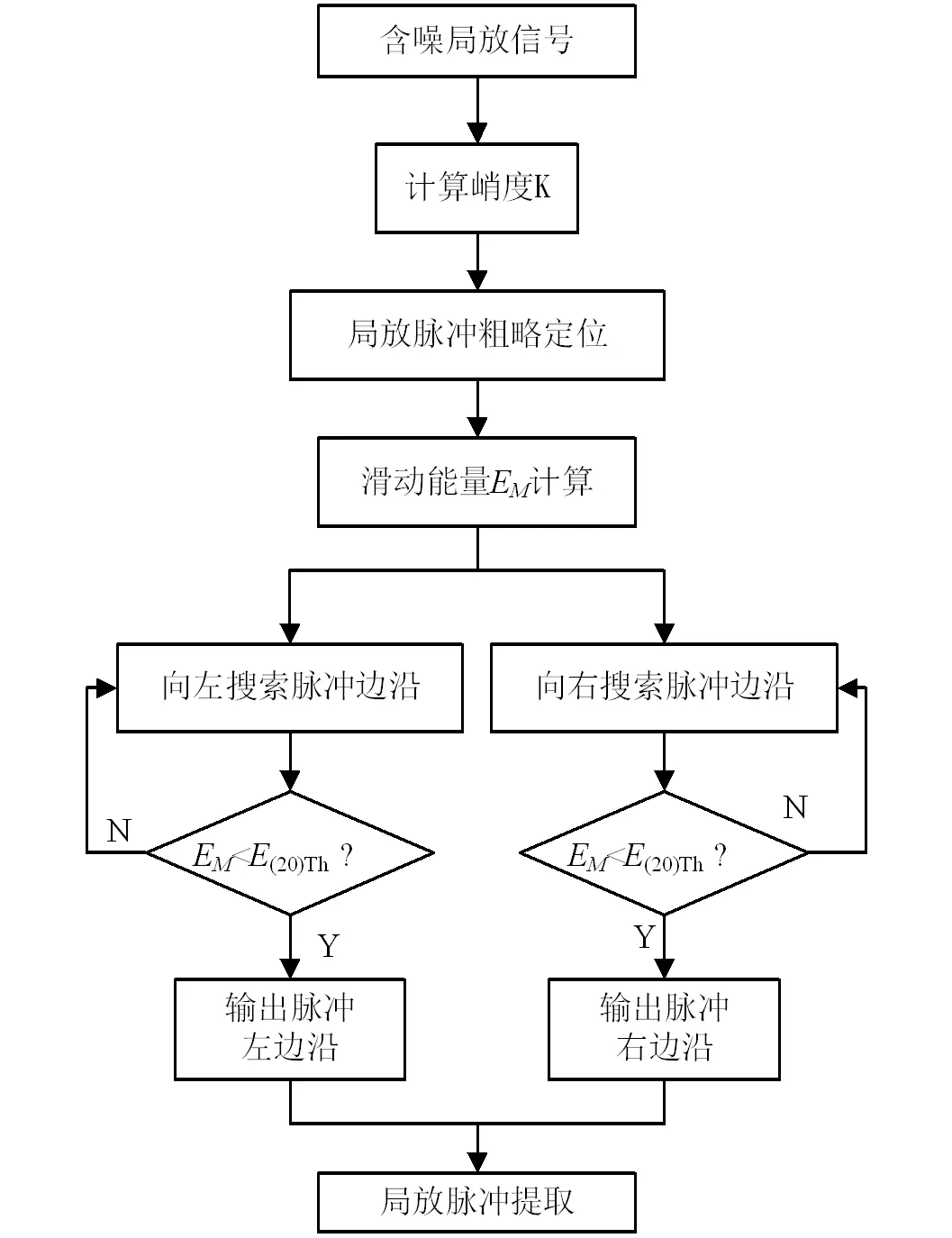
图1 本文方法流程图

4 仿真验证

实际的电力电缆局部放电信号经常表现为一种衰减振荡形式，理论分析时通常采用指数衰减振荡函数模拟局部放电信号[4,10]。因此本文采用以下3种数学模型模拟局部放电信号。

图2a所示的指数衰减型：

图2b所示的单指数衰减振荡型：

(14)

图2c所示的双指数衰减振荡型：

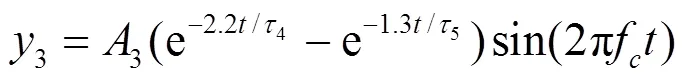
a. 指数衰减型

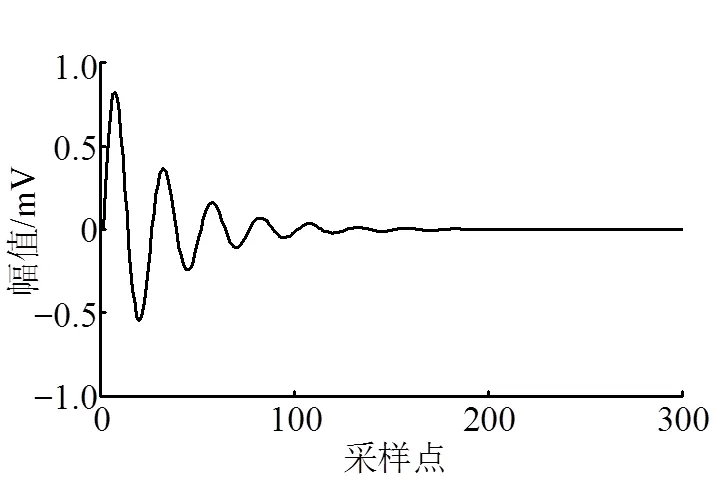
b. 单指数衰减振荡型

c. 双指数衰减振荡型

图2 3种局部放电信号

为了使仿真的电力电缆局部放电信号更接近与实际的局部放电信号，用高斯白噪声模拟背景噪声(信噪比：2.194 dB)，图3a为理想局部放电信号，图3b为加噪后的局部放电信号。

a. 理想局部放电信号

b. 加噪局部放电信号

图3 局放仿真信号

根据前文的理论分析最终本文数据窗长度取20计算信号峭度，图4为含噪局部放电信号的峭度值分布图。

在表2中列出了局部放电仿真信号峭度值突变处的相关参数。根据表2定位局部放电脉冲在整个信号序列中的位置为第250采样点处、第810～830采样点处、第1 510～1 530采样点处。再以局部放电脉冲所在数据窗的中点为中心向左向右通过时域滑动能量搜索的方法寻找脉冲边沿。局部放电仿真信号的时域能量分布如图5所示，图中虚线为能量阈值。

图4 局部放电仿真信号峭度值

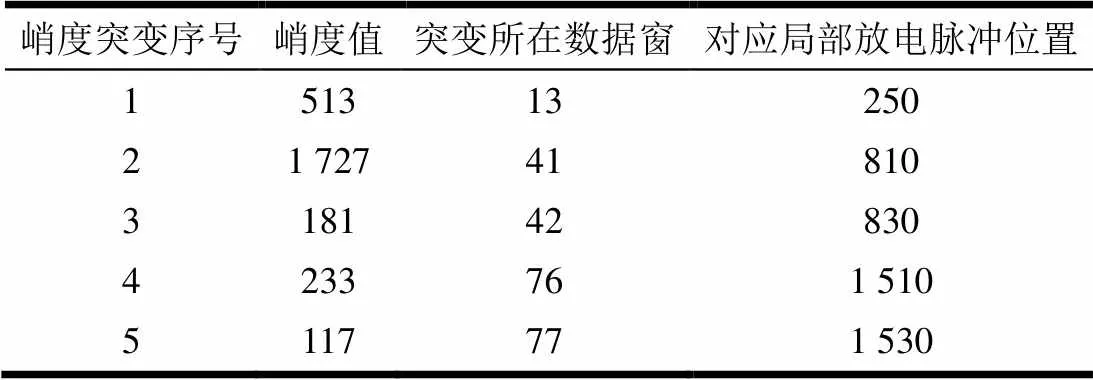
表2 峭度值突变处参数统计

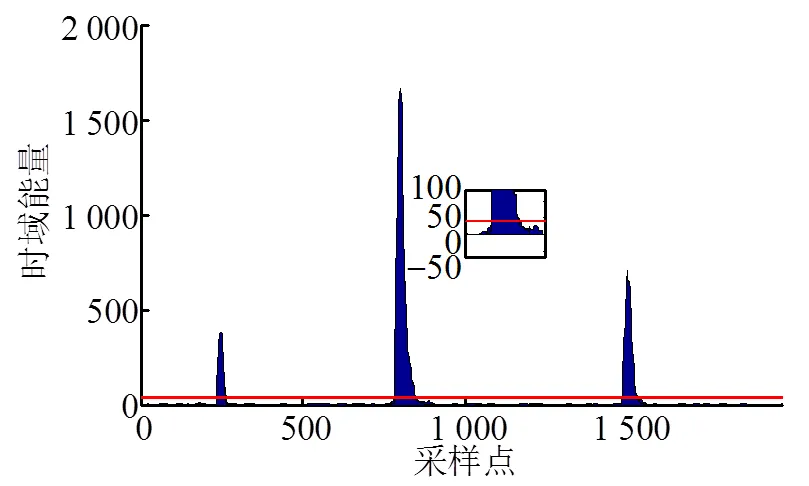
图5 时域能量分布

选用小波去噪方法、EMD去噪法与本文方法对局放信号提取的结果进行比较，如图6所示。小波基选取的是与本文仿真局部放电信号匹配较好的db8小波。

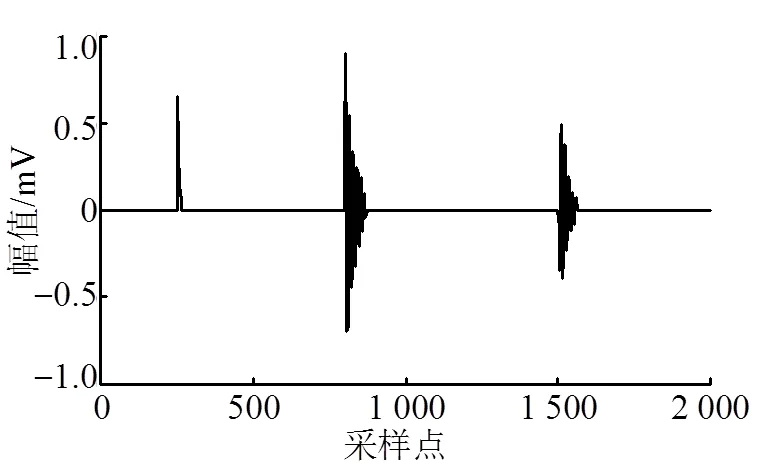
a. 本文方法

b. 小波去噪

c. EMD去噪

表3列出了本文方法和小波方法、EMD去噪法去噪后的信噪比(SNR)、信噪比增益、均方根误差(RSME)、相关系数4种性能指标[4]。

表3 本文方法与小波方法、EMD法去噪性能指标比较(信噪比为2.194 dB)

从图6和表3中可见，原始信噪比为2.194 dB时，本文方法对与局部放电脉冲的提取和噪声的抑制有很好的效果，失真度小，处理后的信号波形与理想局部放电信号波形相似度高。通过信噪比(SNR)、信噪比增益、均方根误差(RSME)、相关系数这4个性能指标的比较，看出本文方法比小波方法、EMD去噪法的各方面性能都好。

5 实验验证

为检验本文方法对实际局放信号的提取能力，以较常见的电力电缆典型环割缺陷作为局放源。图7为人工制作的电缆终端典型缺陷，环割深度2 mm、宽度2 mm，图8为实验过程中测到的局部放电信号波形，其幅值进行了归一化处理，采样率为12.5 MHz。本文方法和小波方法、EMD去噪法处理后的信号如图9所示。

图7 电缆终端主绝缘割伤

图8 实验室测量局部放电信号

a. 本文方法

b. 小波去噪

c. EMD去噪

可以明显看出，图9a相对于图9b、图9c在噪声分布的信号段明显没有毛刺，局放脉冲提取效果显而易见，可见，本文方法明显优于小波方法和EMD方法。

6 结束语

本文提出一种电力电缆局部放电脉冲提取方法，并通过仿真及实测信号验证了该方法的有效性，具有以下特点：

1) 通过计算含噪电力电缆局部放电信号峭度，实现局部放电脉冲的定位，确定局部放电脉冲峰值在整个数据窗中的位置，进而减小后续脉冲提取的计算量。

2) 确定时域能量阈值及对应的时窗长度，采用时域能量搜索的方法，可实现局部放电脉冲边沿检测及确定，进而实现局部放电脉冲提取。

3) 仿真验证及实验验证结果表明：本文方法与小波方法、EMD去噪法相比其各项指标均优于小波方法、EMD去噪法，局部放电脉冲提取结果准确性高且波形无畸变，较好保留电力电缆局部放电信号的特征，便于后续分析。

[1] ASHTIANI M, SHAHRTASH S. Partial discharge pulse localization in excessive noisy data window[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 428-435.

[2] 姚陈果, 陈昱, 陈攀, 等. 基于信号能量谱特征的局部放电故障识别方法及其系统实现[J]. 高电压技术, 2014, 40(3): 829-836.

YAO Chen-guo, CHEN Yu, CHEN Pan, et al. Method for partial dis-charge pattern recognition based on characteristics of signal energy spectrum and its system realization[J]. High Voltage Engineering, 2014, 40(3): 829-836.

[3] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, the Royal Society, 1998, 454(1971): 903-995.

[4] 许中荣, 唐炬, 张晓星, 等. 应用复小波变换对电力变压器局部放电超高频信号去噪研究[J]. 电力自动化设备, 2008, 28(1): 27-32.

XU Zhong-rong, TANG Ju, ZHANG Xiao-xing, et al. Denoising of UHF partial discharge signal by complex wavelet transform for power transformer[J]. Electric Power Automation Equipment, 2008, 28(1): 27-32.

[5] 陈刚, 刘志刚, 张巧革. 一种基于谱峭度的局部放电信号提取新方法[J]. 电力自动化设备, 2013, 33(8): 94-100.

CHENG Gang, LIU Zhi-gang, ZHANG Qiao-ge. Partial discharge signals extraction based on spectral kurtosis[J]. Electric Power Automation Equipment, 2013, 33(8): 94-110.

[6] DWYER R F. Detection of non-Gaussian signals by frequency domain kurtosis estimation[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP'83. [S.l.]: IEEE, 1983, 8: 607-610.

[7] 尚海昆, 苑津莎, 王瑜, 等. 平移不变小波迹消噪方法在局部放电检测中的应用[J]. 电工技术学报, 2013, 28(10): 33-40.

SHANG Hai-kun, YUAN Jin-sha, WANG Yu, et al. Application of wavelet footprints based on translation- invariant in of partial discharge signal detection[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 33-40.

[8] DRAGOTTI P L, VETTERLI M. Wavelet footprints: Theory, algorithms, and applications[J]. IEEE Transactions on Signal Processing, 2003, 51(5): 1306-1323.

[9] GU F C, CHANG H C, KUO C C. Gas-insulated switchgear PD signal analysis based on Hilbert-Huang transform with fractal parameters enhancement[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(4): 1049-1055.

[10] 王永强, 谢军, 律方成. 基于改进量子粒子群优化稀疏分解的局放信号去噪方法[J]. 电工技术学报, 2015, 30(12): 320-329.

WANG Yong-qiang, XIE Jun, LÜ Fang-cheng. PD signal denoising method based on improved quantum-behaved particle swarm optimization sparse decomposition[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 320-329.

[11] 李永刚, 赵辰, 吕黔苏, 等. 基于傅里叶变换的GIS局部放电信号处理研究[J]. 华北电力大学学报, 2012, 39(5): 28-34.

LI Yong-gang, ZHAO Chen, LÜ Qian-su, et al. Signal processing of the GIS'partial discharge based on Fourier transform[J]. Journal of North China Electric Power University (Natural Science Edition), 2012, 39(5): 28-354.

[12] 张晓星, 周君杰, 李楠, 等. 抑制局部放电白噪声的分块阈值空域相关联合去噪法[J]. 高电压技术, 2011, 37(5): 1142-1148.

ZHANG Xiao-xing, ZHOU Jun-jie, LI Nan, et al. Block theresholding spatial combined de-noising method for suppress white-noise interference in PD signals[J]. High Voltage Engineering, 2011, 37(5): 1142-1148.

[13] 胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012, 32(11): 106-111.

HU Ai-jun, MA Wan-li, TANG Gui-ji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11): 106-111.

[14] LIU Hui, CHEN Yu-feng, SHEN Qing-he, et al. Cluster analysis on signals from XLPE cable partial discharge detection[C]//2014 International Conference on Power System Technology (POWERCON). [S.l.]: IEEE, 2014: 1535-1540.

编 辑 漆 蓉

Partial Discharge Pulse Extraction Algorithm Based on Kurtosis and Time Domain Energy

ZHANG An-an1, HE Cong1, SUN Mao-yi2, and LI Qian1

(1. School of Electrical Engineering and Information, Southwest Petroleum University Chengdu 610500; 2. China National Institute of Measurement and Testing Technology Chengdu 610021)

This paper proposes a power cable partial discharge (PD) pulse extraction method. Firstly, the PD pulse peak is located according to the variation of signal kurtosis, and then according to the signal energy’s changing the method of sliding energy search is adopted to calculate and search the edge of PD pulse from the centered PH pulse to the both sides, so as to extract the PD pulse in the noise background accurately. This method can distinguish the full noise signal section from the section that contains partial discharge pulse signal in partial discharge detection signal, and won’t be constrained by the number of partial discharge pulses and position of pulse, and also has features of simple step and small amount of calculation. By comparing the simulation experiments of two mainstream power cable PD pulse extraction methods (the wavelet threshold de-noising and the empirical mode decomposition) with the actual experiments, the effectiveness and veracity of this method have been verified.

kurtosis; partial discharge (PD); partial discharge pulse extraction; time domain sliding energy

TM835

A

10.3969/j.issn.1001-0548.2017.04.014

2016-04-26；

2016-11-15

国家自然科学基金(51107107)；中国博士后基金(2014M562335)；四川省教育厅科研创新团队(自然科学)项目(15TD0005)

张安安(1977-)，男，博士，副教授，主要从事电气设备检测及高电压技术方面的研究.