基于复模型的模拟电路故障诊断
2017-10-13杨成林
高 媛,杨成林
基于复模型的模拟电路故障诊断
高 媛,杨成林
(电子科技大学自动化工程学院 成都 611731)
参数故障诊断和容差问题是模拟电路故障诊断的两个主要难题。该文从故障建模入手,提出一种新的复数域参数故障统一建模方法。模拟电路输出电压的实部和虚部都是故障元件参数的函数,联立实部和虚部函数,并消掉被建模元件参数,得到与参数无关的函数。该函数只由电路结构、故障元件位置和无故障元件的参数确定。因此,以它作为故障模型就与参数无关,能描述任何参数漂移、开路和短路故障。该模型函数是二次函数,除了无故障点之外,不同元件的模型函数会在复平面上相交于第二个点,称为混叠问题。该文采用多频方法来消除此混叠现象。仿真结果验证了方法的有效性。
混叠问题; 模拟故障诊断; 复平面; 故障模型; 容差
模拟电路故障诊断方法通常分为测前仿真(SBT)和测后仿真(SAT)两大类[1]。故障字典法[2-4]是使用最为广泛的SBT方法之一,它最适用于硬故障(开路和短路)诊断[3]。文献[5]建立了一种节点电压灵敏度序列的故障字典方法,一个元件对应一个特征码,该方法适用于软故障和硬故障。文献[6]将文献[5]的方法扩展至非线性电路。文献[7]提出了一种基于“节点电压灵敏度权序列不变法”的新的故障字典法,文献[8]提出一种基于斜率的故障诊断方法。文献[9]在文献[8]的基础上改进了这种方法后,故障字典法能够理论上完成单个或多个故障诊断及在一定程度上处理容差。以上方法多基于二维空间,文献[10]提出了基于高维空间的曲线诊断方法。尽管文献[11-14]给出了许多基于人工智能的数据方法,但故障字典法依然是被广泛应用的最成熟的技术之一。如果研究一种故障建模方法能对软硬故障同时进行统一建模,且能将模型存储于故障字典中,那么则有利于故障字典方法继续发挥作用。鉴于此,本文在统一的故障建模方法基础上研究频率选择法,这些被选频率将被保存在故障字典中,用于将来发生故障信号混叠时的故障诊断。
1 复平面建模基本理论
1.1 理论基础
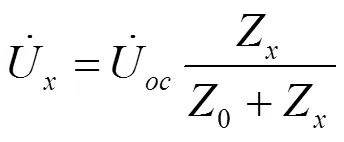
(2)

(4)

(5)
不失一般性,做如下替换:
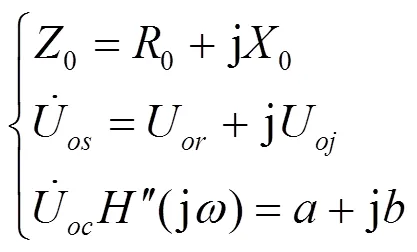
(7)
如果元件是电阻,可以推导得到:
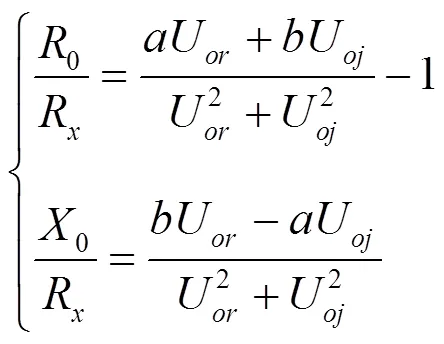
根据式(8),消掉R,得到:
(9)
式(9)中共有6个参数,如前文所述0和0都独立于故障元件参数值。从式(6)可以看出,和是由和共同确定的,而它们都是独立于故障元件参数值,因此和也独立于故障元件参数。和是输出电压实部和虚部。所以无论故障源发生何种(参数漂移、软、硬)故障,式(9)都成立。式(9)由在中的位置确定,因此,和组成的关系式可以视作故障模型,式(9)可以表示为:
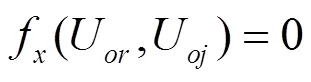
式(10)同时适用于软硬故障,是统一的故障建模方法。如果故障为电容或者电感元件,可以推导得到相同结论。本文以式(10)为故障模型,进行故障诊断。后文的仿真结果就是直接以和的关系曲线(由式(10)所确定)作为故障特征来进行故障诊断。由于、、和也是关于频率的函数,式(10)也可以写成:
(11)
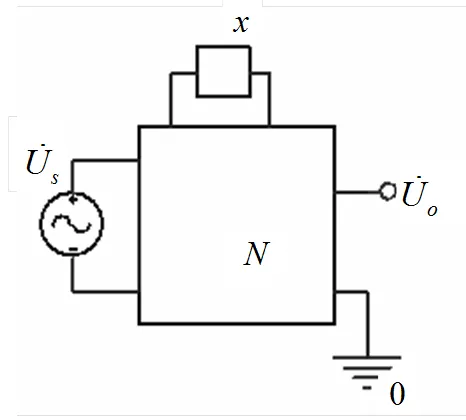
a. 无故障网络 b. 等效网络
c. 电压源单独作用 d. 等效故障源单独作用
图1 建模基本理论
1.2 基于故障建模的仿真
对于大多数电路,很难获得式(10)的显式表达,实际上此表达也并不是必需的,可以通过仿真获得其在复平面上的图形化表达。具体仿真步骤如下:
1) 选定激励信号幅度与频率。
2) 对每个潜在故障元件进行参数扫描仿真。每个元件x的故障参数扫描范围(包括无故障)为:
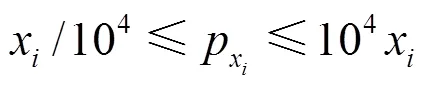
3) 将得到的一系列输出电压分解为实部和虚部两部分,在复平面上描出并拟合成光滑曲线。
不同的曲线代表不同故障源的特征曲线,作为故障特征保存在故障字典中。有些故障源具有相同的特征曲线,这些具有相同曲线的故障源被称为模糊组。需要指出的是,所有的特征曲线都经过同一点(无故障点),即无故障电压在复平面上的坐标点。不难看出式(9)是二次函数,因此不同的特征曲线除了无故障点外,还可能有第二个交点。这是不同元件的特定故障参数导致相同输出电压造成的,本文称为混叠现象,下面介绍其解决方法。
2 消除混叠现象和容差问题的方法
在模拟电路中,电路元件的参数从其标称值开始,在规定误差范围(如±5%)变化,称为容差范围,参数在范围内变化不被视为故障。如果两个故障源的特征曲线比较接近,由于容差的影响,这些元件故障可能在实际电路中无法被区分,会诱发故障诊断错误。另外,由于两个元器件在复平面内具有不同的二次曲线,所以这两条曲线在平面内除了无故障点外还可能有交点,即混叠问题。
2.1 容差处理
当电路工作稳定时无故障元件的参数近似认为是不变的,此时的工作电压记为。即使具有相同的电路结构和参数,由于具体对象工作环境的不同,不同电路会有不同的。此时,故障的特征曲线可用实际的值进行矫正计算。通过下面的矫正公式补偿该无故障点的偏移量为:

(14)
2.2 消除混叠问题
线性非时变电路,频率响应函数可以表达为:

单故障假设条件下,频率响应函数是x和频率的函数,有:
(16)
对于任何两个故障源的x和x,必有特定的故障参数和使下面的等式成立:

3 故障诊断方法实现
故障诊断流程如图2所示。

图1 故障诊断流程
步骤1) 通过第1节提出的故障建模方法,仿真获得被测电路在频率处的特征曲线,并存储于故障字典中。
步骤2) 对任何一对可以区分的故障(x, x),找出在复平面上的特征曲线有交集的点(除了无故障点)。同时得到输出电压相对应的故障参数(x, x)。对于任何一对故障(x, x),执行下面的频率选择步骤。
①设置x=x,所有其他元件都无故障。通过PSPICE的频率扫描功能,得到。设置x=x,所有其他元件都无故障,得到。
4 实例验证
以跳藕滤波电路为例,如图3所示,激励信号为1 kHz、5 V的正弦信号,代表测点。

图3 跳藕滤波器
1) 故障字典构建
该图表明这些元件可以划分为如表1所示的模糊组,每个模糊组的特征曲线存储于故障字典中。基于本文的建模方法,模糊组是由于测点选择不合理,或者测点不够造成的(如7号模糊组可以通过在第5个运放后面增加测点被分成两个模糊组)。关于测点选取问题,将不在本文中讨论。这些曲线中的交点(除了无故障点),代表某相关元件的特定参数故障在此频率下产生了特征混叠现象。以1(1号曲线) 和3(10号曲线)为例,尽管它们的曲线不同,但是1=3 728W和3=73.5 nF时,被测电路的输出电压均为V,它们在当前频率下不能被区分。此混叠问题用第3.2部分介绍的方法进行处理。保持1=3 728W不变,其他元件无故障。通过Pspice进行AC扫描,得到输出电压从1~10 kHz的曲线,结果如图5所示。保持3=73.5 nF且其他元件无故障,仿真得到与频率的关系曲线。图6给出了与的距离关系,即。不难看出,在2 381 Hz下可以获得曲线最大距离,= 11.32。在此频率下两元件故障电压分别为=-4.2+j11.9 V和=1.7+j2.2j V。、、和=2 381 Hz都被记录在故障表2中,为故障诊断做准备。所有其他的混叠问题也用相同的方法进行处理,结果如表2所示。

图4 故障特征曲线

表1 被测电路模糊组
2) 故障诊断
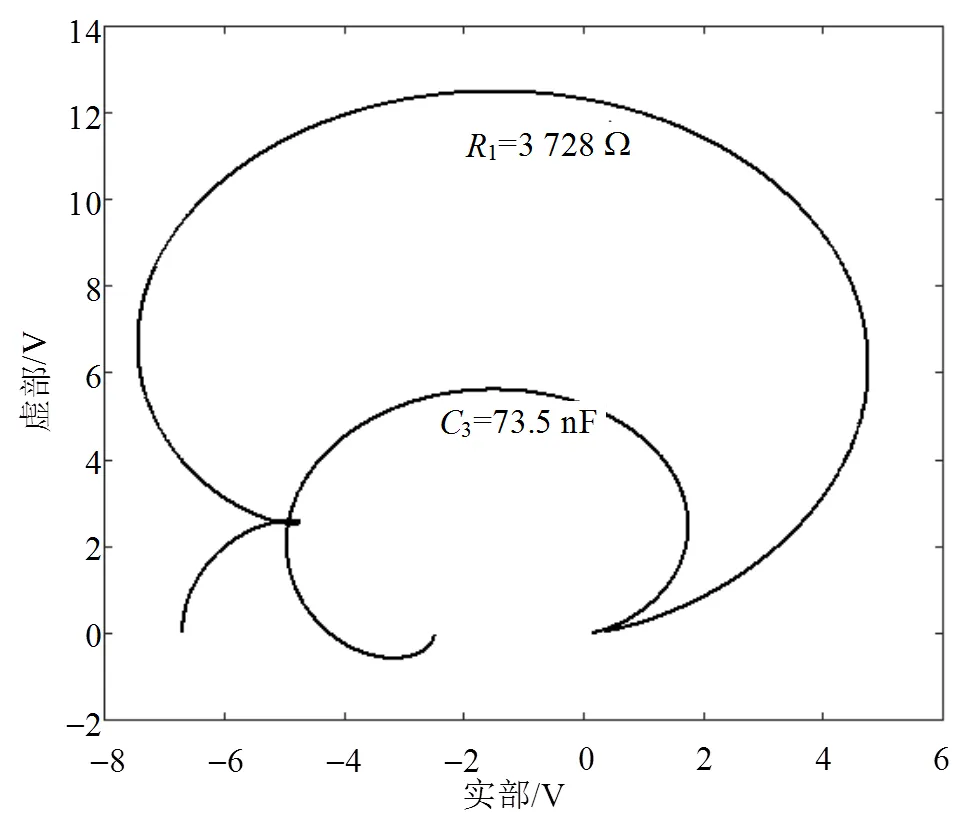
图5 不同频率下的故障电压实部和虚部曲线
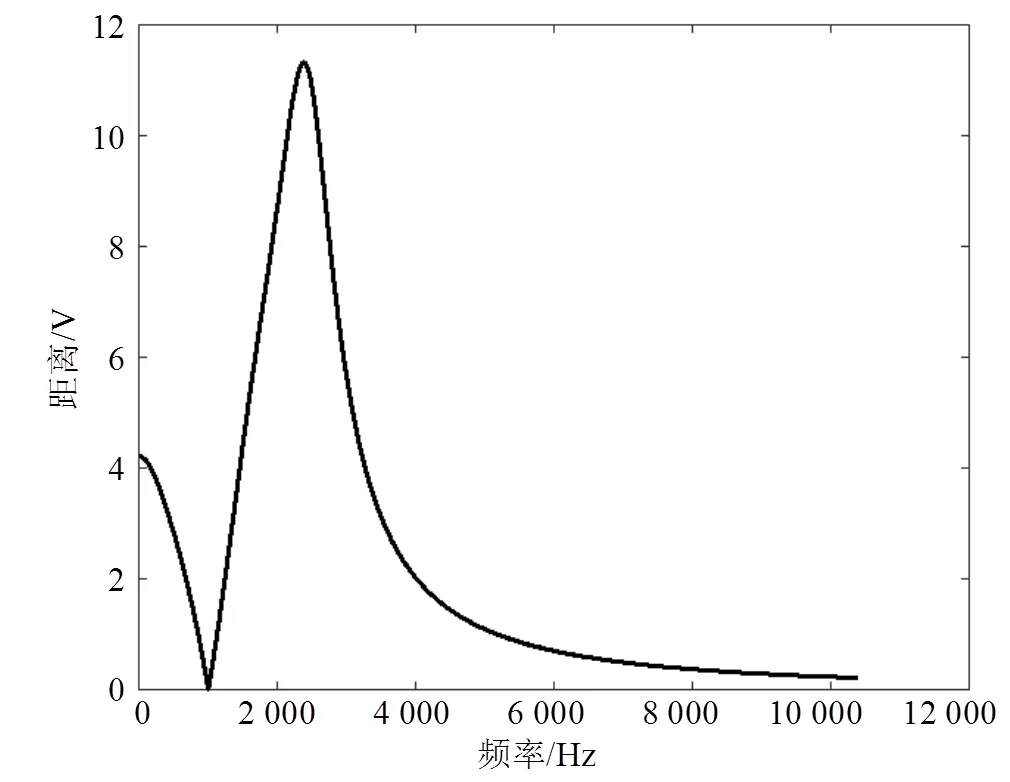
图6 不同频率下的故障电压曲线欧式距离
但同时也不难发现有一些其他的故障元件的特征曲线与3特征曲线相交,如图4中的‘’、‘’、‘’3点所示,是一个混叠问题。以图4中‘’点为例,该点电压为=-4.88+j2.55 V,由故障3= 73.5 nF产生。从表2查出=-4.88+j2.55 V与-4.93+j2.62 V最为接近,它是1=3 728W与3= 73.5 nF的公共点。用区分此二故障的敏感频率(2 381 Hz)来重新仿真CUT,获得此频率下的故障电压=1.67+j2.24 V。从表2可以查出,1.72+j2.22比-4.20+j11.86更接近,因此故障源3即为诊断结果,诊断正确。图4中其他的混叠现象用相同方法处理。通过本文的建模与混叠处理方法,此元件故障正确隔离率为99%。
为了验证本文方法的有效性,进行统计试验。从表1中所列出的所有模糊组选出一个代表元件进行故障模拟,元件正常参数值用表示,模拟(0.01~0.9)(1.1~100)参数范围内所有故障情况,采用对数扫描方式,每10倍参数取10个点。因此每个元件故障数目共计39个,其他无故障元件参数在其容差范围内(0.9~1.1)随机取值,混叠点附近的参数采用前文所述方法进行处理。总共进行100次蒙特卡洛仿真,故障诊断结果如表3所示。
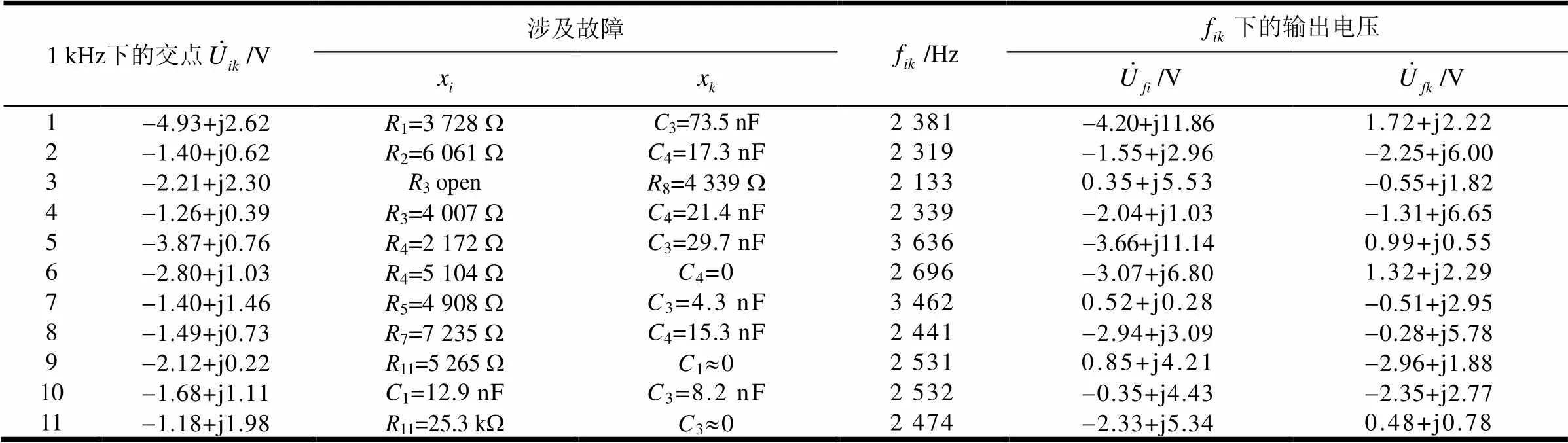
表2 故障字典

表3 故障正确隔离率
本文假定所有故障发生先验概率相同,因此隔离率就是隔离出的故障与所有可能故障的比例。从表3可以看出,故障源4、2和3的诊断精度较低,主要是在此频率下,它们的特征曲线在虚部为(-2~0)实部为(0~1)时比较接近,如图4所示,造成故障诊断率较低。这也可以通过改变建立字典的频率来缓解,或者增加故障字典频率,即建立多个频率下的图4所示的字典,来增加故障正确隔离率。
5 结束语
基于两个测点信号和文献[8]中斜率的建模方法能够解决线性模拟电路的软故障诊断问题,本文提出一种新的复数域参数故障统一建模方法,该方法能解决软硬故障的统一建模问题,只需要一个测点,且故障分辨率更高,因此特别适用于没有内部测点的模拟电路故障诊断。针对复模型中,某些具有不同特征的故障元件的某些特定参数故障会产生相同的故障电压的问题,本文提出了一种基于频率敏感的频率优选方法来进一步区分混叠故障。再结合容差处理方法,本文方法能够精确地实现故障定位。通过仿真以及实验验证了本文方法的有效性。如果进一步增加测点,本文的方法能够推广应用于多故障诊断,理论上,如果测点数目为,则能够建模的多故障情况为2-1。
[1] BANDLER J W, SALAMA A E. Fault diagnosis of analog circuits[J]. Proceedings of the IEEE, 1985,73(8): 1279-1325.
[2] HOCHWALD W, BASTIAN J D. A DC approach for the analog fault dictionary determination[J]. IEEE Trans Circuits Syst, 1979, CAS-26: 523-529.
[3] LIN P M, ELCHERIF Y S. Analogue circuits fault dictionary – new approaches and implementation[J]. Inl J Circuit Theory Appl, 1985, 13: 149-172.
[4] JANUSZ A S, LIU Dong, LIU Zhi-Hong, et al. Entropy-based optimum test nodes selection for the analog fault dictionary techniques[J]. IEEE Trans Instrum Meas, 2004, 53: 754-761.
[5] LI Feng, WOO P Y. The invariance of node-voltage sensitivity sequence and its application in a unified fault detection dictionary method[J]. IEEE Trans Circuits Sys I, 1999, 46: 1222-1227.
[6] 谭阳红, 何怡刚. 模拟电路故障诊断的新故障字典法[J]. 微电子学, 2001, 31(4): 252-254.
TAN Yang-hong, HE Yi-gang. A new fault dictionary method for fault diagnosis of analog circuits[J]. Microelectronics, 2001, 31(4): 252-254.
[7] 张伟, 许爱强, 陈振林. 模拟电路节点电压灵敏度权序列故障字典法[J]. 电子测量与仪器学报, 2006, 20(4): 46-49.
ZHANG Wei, XU Ai-qiang, CHEN Zhen-lin. Fault dictionary method in analog circuits based on node voltage sensitivity weight sequence[J]. Journal of Electronic Measurement and Instrument, 2006, 20(4): 46-49.
[8] WANG Peng, YANG Shi-yuan. A soft fault dictionary method for analog circuit diagnosis based on slope fault mode[J]. Control and Automation, 2006, 22(6): 1-23.
[9] WANG Peng, YANG Shi-yuan. A new diagnosis approach for handling tolerance in analog and mixed-signal circuits by using fuzzy math[J]. IEEE Trans on Circuits and Systems-I: Regular Papers, 2005, 52: 2118-2127.
[10] CZAJA Z, ZIELONKO R. Fault diagnosis in electronic circuits based on bilinear transformation in 3-D and 4-D spaces[J]. IEEE Transactions on Instrumentation and Measuremet, 2003, 52: 97-102.
[11] TAN Y, HE Y, CUI C, et al. A novel method for analog fault diagnosis based on neural networks and genetic algorithms[J]. IEEE Trans Instrum Meas, 2008, 57(11): 2631-2639.
[12] GRZECHCA D, GOLONEK T, RUTKOWSKI J. The use of simulated annealing with fuzzy objective function to optimal frequency selection for analog circuit diagnosis[C]//14th IEEE International Conference on Electronics, Circuits and Systems. Marrakech, Morocco: IEEE, 2007: 899-902.
[13] YUAN Li-fen, HE Yi-gang, HUANG Jiao-ying, et al. A new neural-network-based fault diagnosis, approach for analog circuits by using kurtosis and entropy as a preprocessor[J]. IEEE Trans Instrum Meas, 2010, 57(3): 586-595.
[14] DENG Yong, SHI Yi-bing, ZHANG Wei. An approach to locate parametric faults in nonlinear analog circuits[J]. IEEE TransInstrum Meas, 2012, 61(2): 358-367.
编 辑 漆 蓉
Complex Fault Modeling Based Analog-Circuit Fault Diagnosis
GAO Yuan and YANG Cheng-lin
(School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 611731)
Parameter fault and tolerance are two challenging problems in analog circuit fault diagnosis. This paper proposes approaches to solve such problems. First, a new fault modeling method and its theoretical proof are presented. In analog circuits, both the real part and the imaginary part of output voltage are the functions of fault component parameters. By eliminating component parameters from the simultaneous formulas, a new equation is achieved. It is independent from the value of component parameters and uniquely determined by the component locations and the topological structure. Hence, the function can be used as the fault model, which is applicable to both hard (open or short) and soft (parametric) faults. It is also applicable to either linear or nonlinear analog circuits. Then, the parameter tolerance is taken into consideration. A frequency selection method is proposed to maximize the difference between fault signatures. Hence, the aliasing problem arise from tolerance can be mitigated. The effectiveness of the proposed approaches is verified by simulated results.
aliasing problem; analog fault diagnosis; complex plane; fault modeling; tolerance
TN707
A
10.3969/j.issn.1001-0548.2017.04.011
2014-02-24;
2016-03-06
国家自然科学基金(61201009,61271035)
高媛(1979-),女,博士生,研究员,主要从事电子系统测试与测试性设计方面的研究.
