基于尺度函数的插值小波构建方法

张治国，胡学海，周 依



基于尺度函数的插值小波构建方法

张治国，胡学海，周 依

(电子科技大学自动化工程学院 成都 611731)

经典小波采样理论应用正交小波构建插值小波，然而正交小波的解析表达式通常比较复杂或难以获得，因此在实践中确定和构建插值小波，成为信号处理及调和分析领域研究的重要课题。为此，提出一种构建插值小波的新方法。该方法应用尺度函数构建插值小波，避免了对正交小波的求解，提高了构建插值小波的效率。以Daubechies和Coiflets多分辨分析为例，验证了该方法的正确性和有效性。

插值基; 插值小波; 多分辨率分析; 小波采样

1989年，文献[1]给出一种利用正交小波构建插值小波的通用方法，提出小波采样理论。由于插值小波可以有效提高小波变换的效率，因而迅速得到广泛应用[2-5]，逐渐成为离散信号处理领域的重要工具。然而在该算法中，插值小波的构建依赖于正交小波的自相关函数，因此在获得插值小波的同时，往往很难得到其相对应的尺度函数，故该插值小波常常不能在多分辨分析中实现信号的正交分解。

为解决上述问题，文献[6-8]提出采用正交小波线性组合的方法来构建插值小波。这些构建算法的提出不仅促进了插值小波在图像处理[9-10]、仿真[11]、控制[12]以及信号处理[13]等领域更广泛的应用，而且还使得与其相关的采样理论，如：非均匀采样理论[13]、平移不变空间采样理论[14]以及混叠理论[15]得到长足发展。然而应用这类方法构建插值小波，必须首先得到正交小波的解析表达式，但表达式比较复杂，因此使用这类方法构建插值小波的效率较低。

针对上述问题，本文将重点研究插值小波和尺度函数之间的相互关系，提出一种利用尺度函数构建插值小波的通用方法，以提高插值小波的构建效率。

1 插值滤波器的特殊频域表达

但相关结果可以通过Zak变换或坐标平移的方式推广到插值点在其他位置的情况[17]。与此同时，由于尺度为的插值小波可以通过尺度为的插值小波通过变量代换直接获得，因此仅讨论应用尺度函数构建尺度为的插值小波。

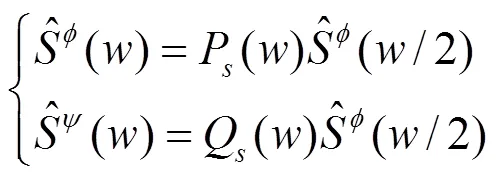
对式(3)两边进行傅里叶变换，可得：

(4)

根据Poissson公式：

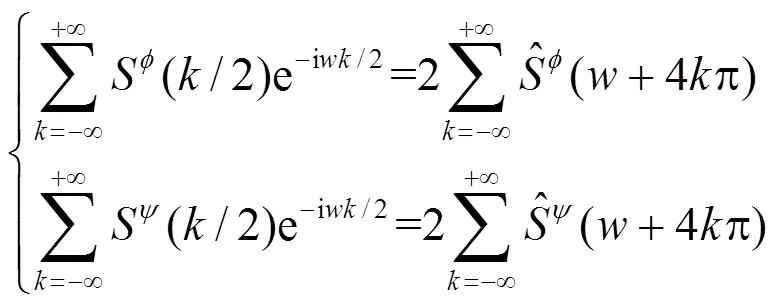
因此式(4)又可以进一步表示为：

(6)

即：

由式(7)可知，插值滤波器在频域中的表达形式很特殊，即它们是插值函数的傅里叶变换和以为周期的延拓。该性质对于应用尺度函数构建插值小波具有十分重要的作用。

2 小波空间正交性与插值滤波器的相互关系

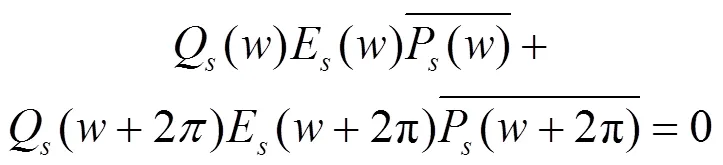
式中，

(9)

证明：由Parseval恒等式可知：

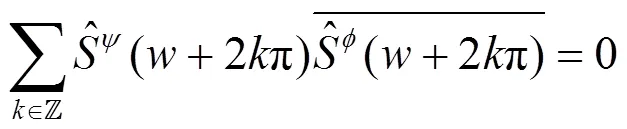
另一方面，由式(7)可知：

(12)

以及

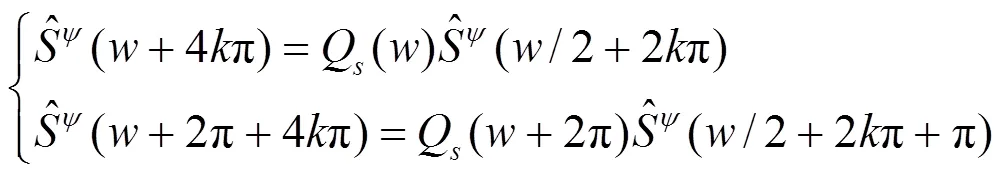
将式(12)和式(13)带入式(11)，可得：

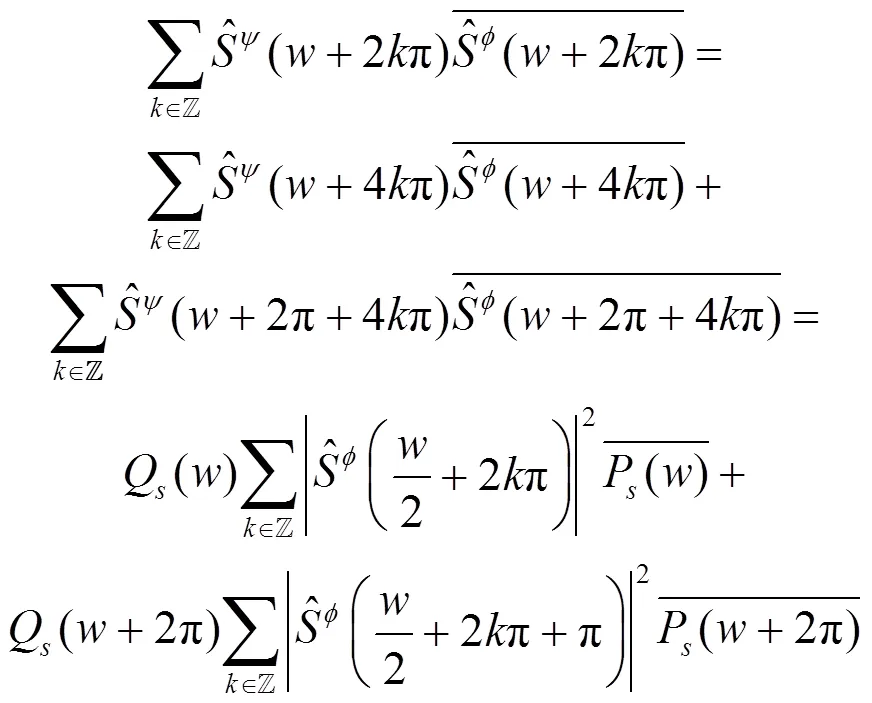
再将式(11)和式(9)代入式(14)，即得到式(8)。

3 插值高通滤波器的构建

插值小波的获得，关键在于构建其对应的滤波器，即高通滤波器。基于前两节的讨论，本节将提出一种基于插值低通滤波来获得插值高通滤波器的方法。该方法可以表述为如下定理。

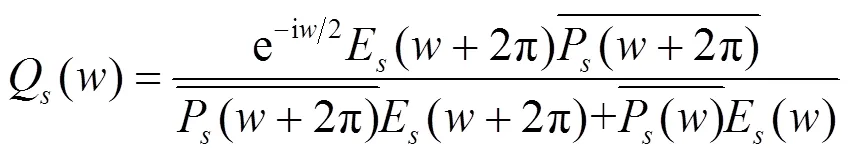
证明：由文献[7]可得：

(16)

由式(7)和式(16)可得：

由式(17)可知：

(18)

将式(8)代入式(18)，有：

式(15)成立。

4 插值小波的构建

如果获取了插值高通滤波器，那么插值小波的傅里叶变换就可以表示为式(2)中第二个等式的形式。将式(15)代入该等式可得：

进一步将式(7)和式(9)代入式(20)，可得：

(21)

(23)

式中，

以及

由式(23)可知，只要获得正交尺度函数就可以得到相应的插值小波。这有效地避免了在传统构建算法中，先构建正交尺度函数，再由正交尺度函数构建正交小波，最后由正交小波构建插值小波的繁琐过程，因而式(23)大大简化了插值小波的构建过程。

5 算例

Daubechies和Coiflets小波被广泛应用于图像分析和信号检测，这里将以二阶Daubechies和三阶Coiflets小波为例，验证本文提出的插值小波构建算法的有效性。

5.1 基于本文算法的插值小波构建

由于经典小波理论已经详细论述了Daubechies和Coiflets尺度函数的构建及频域表达，因此由式(23)可知，获取关键在于得到和的表达式。

对于二阶Daubechies尺度函数，由Poissson公式及经典小波理论可知：

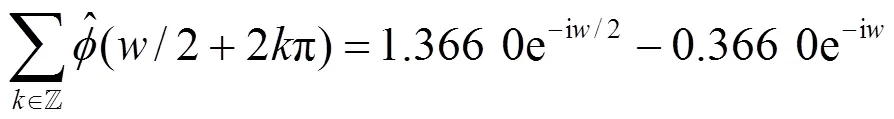
(25)

将式(24)和式(25)代入式(23)即可获得二阶Daubechies插值小波的傅里叶表达式。对其进行傅里叶反变换，其时域形式，如图1a所示。

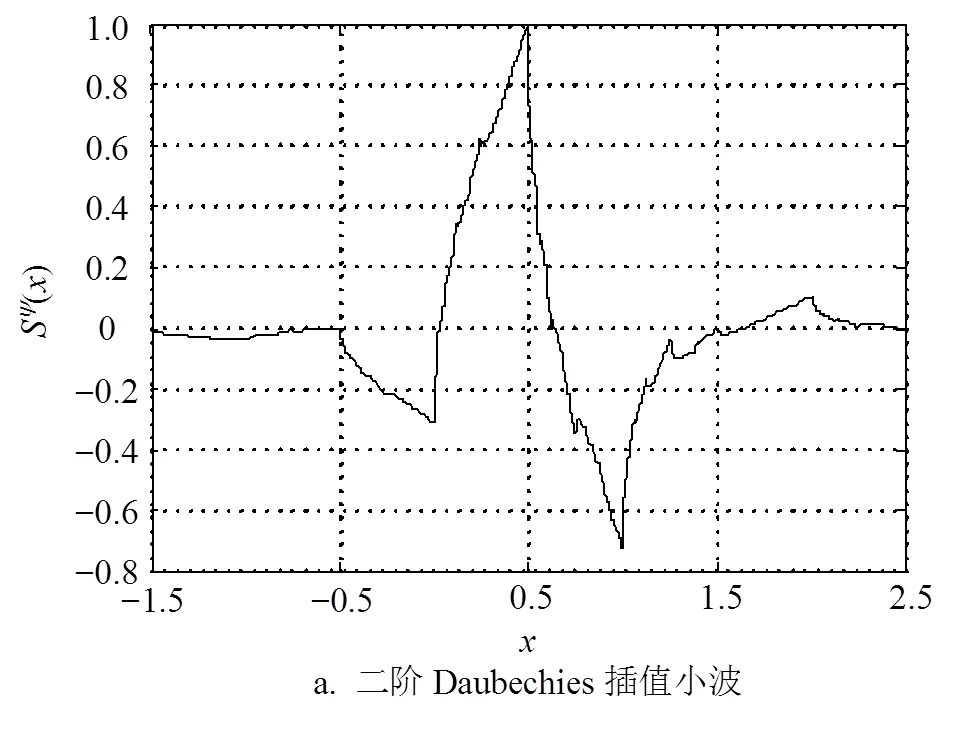
与二阶Daubechies的插值小波类似，由Poissson公式及经典小波理论可知，对三阶Coiflets尺度函数而言，有：

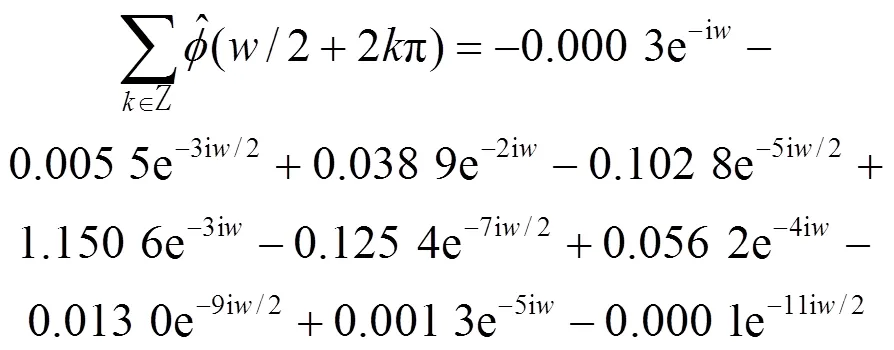
而

(27)

将式(26)和式(27)分别代入式(23)，可得三阶Coiflets插值小波的傅里叶表达式。将三阶Coiflets插值小波的傅里叶表达式，进行傅里叶反变换即可获得三阶Coiflets插值小波，其形式如图1b所示。

5.2 基于经典算法的插值小波构建

上述插值小波也可以通过经典方法构建，即基于正交尺度函数先构建相应的正交小波，再由正交小波应用文献[6]算法得到插值小波。由经典小波理论可知，正交小波的高、低通滤波器可表述为以下关系：

基于经典小波理论，应用式(28)可得二阶Daubechies小波对应的高通滤波器为：

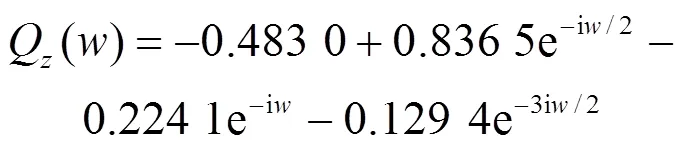
而三阶Coiflets对应的高通滤波器为：

(30)

对于Daubechies和Coiflets小波，由于其解析表达式的获取，依然是小波理论有待解决的难题，因此在实际应用中，常常应用式(29)和式(30)，通过数值迭代来获取它们的数值解。因为该迭代过程较为复杂，所以大大限制了插值小波获取的效率。经过迭代以后获得的正交小波()如图2a和图2b所示。

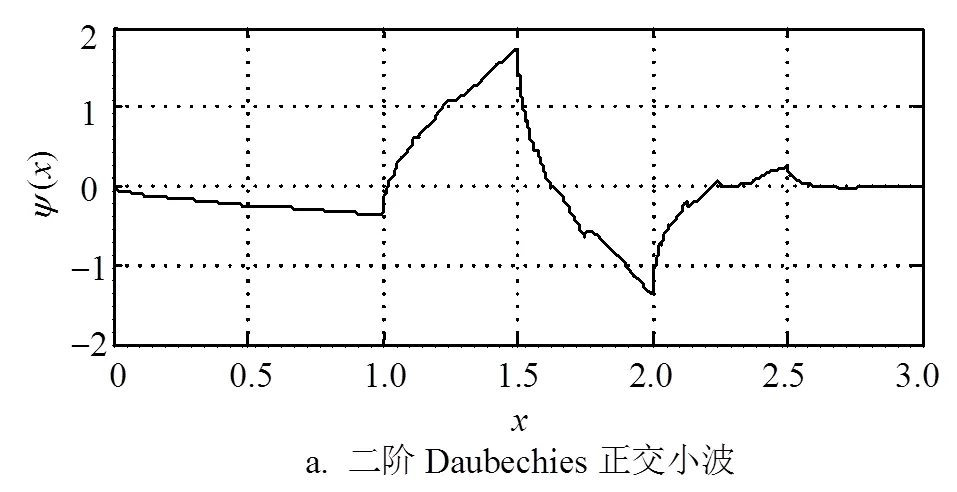
由于无法获得上述两种正交小波的解析表达式，因此通过离散傅里叶变换的方式获得它们的频域表达式，分别如图2c～图2f所示。基于图2所示的傅里叶变换结果，对二阶Daubechies正交小波，近似可得：

而对于三阶Coiflets，近似有：

(32)

5.3 算法对比与插值小波的验证

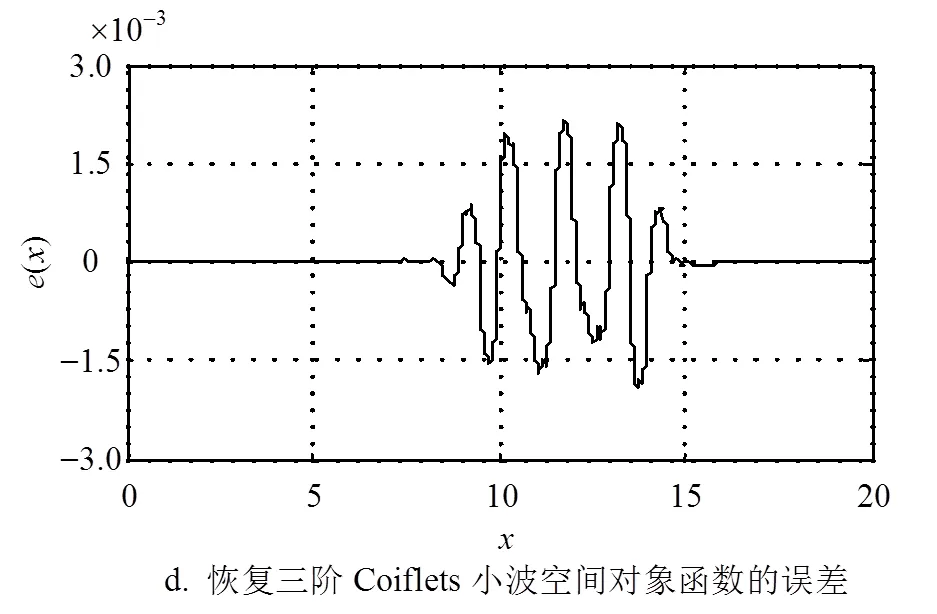
基于上述统计数据，考虑到仿真软件数值计算的误差水平，可以认为基于两种算法构建的插值小波都已经通过式(33)成功还原了二阶Daubechies和三阶Coiflet小波，然而对比误差可以发现，本文提出的算法由于减少了数值计算的步骤，简化了计算过程，其插值获得的还原函数具有更小的逼近误差。这表明本文算法得到的插值小波，具有更高的准确性。与此同时，从两种算法的插值小波构建过程还可以看出，本文提出的算法可以直接由尺度函数获得插值小波，而经典算法需要先获得正交小波，然后再由正交小波构建插值小波。由于正交小波解析表达式常常难以获得或者比较复杂 (如Daubechies和Coif多分辨分析)，因此本文提出的算法还具有更高的计算效率。

6 结束语

插值小波是多分辨分析理论的重要分支，而构建插值小波是其应用的前提和基础。由于经典算法在插值小波构建过程中需要求取正交小波，而正交小波的解析表达式常常比较复杂或难以获得，因此极大地限制了插值小波在信号处理领域的应用。基于小波和尺度函数的特殊联系，本文提出了一种利用尺度函数来构建插值小波的方法。由于该方法避免了对正交小波的求取，因而极大地提高了插值小波的构建效率。本文的理论分析和算例证明了该算法的正确性和有效性。

[1] DONOHO D L. Interpolating wavelet transforms[EB/OL]. [2015-08-10]. http://www.stats.stanford.edu/~donoho/Reports/ 1992/interpol.pdf.

[2] ASAMWAR R S, BHURCHANDI K M, GANDHI A S. Interpolation of images using discrete wavelet transform to simulate image resizing as in human vision[J]. International Journal of Automation and Computing, 2010, 7(1): 9-16.

[3] REINOSO J F, MONCAYO M. Optimal quality for image fusion with interpolatory parametric filters[J]. Mathematics and Computers in Simulation, 2011, 81(7): 2307-2316.

[4] SCHNEIDER K, VASILYEV O V. Wavelet methods in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 2010, 42(3): 473-503.

[5] SUMMER S, JONES C N, LYGEROS J. A multiresolution approximation method for fast explicit model predictive control[J]. IEEE Transactions on Automatic Control, 2011, 56 (11): 2530-2541.

[6] WALTER G G. A sampling theorem for wavelet subspaces[J]. IEEE Transactions on Information Theory, 1992, 38(2): 881-884.

[7] JANSSEN A. The Zak transform and sampling theorems for wavelet subspaces[J]. IEEE Transactions on Signal Processing, 1993, 41(2): 3360-3364.

[8] WEN Chen, ITOH S. On sampling in shift invariant spaces[J]. IEEE Transactions on Information Theory, 2002, 48(10): 2802-2809.

[9] PRIYADHARSINI R, SREE S T, RAJENDRAN V. Underwater acoustic image enhancement using wavelet and K-L transform[J]. IEEE International Conference on Applied and Theoretical Computing and Communication Technology, 2015, 37(2): 564-567.

[10] KUMA R L, KWON G R. New interpolation method based on combination of discrete cosine transform and wavelet transform[J]. IEEE Transaction on Circuits and Systems for Video Techon logy, 2015, 56(3): 363-366.

[11] ERICSSON S. Irregular sampling in shift invariant spaces of higher dimensions[J]. Int J, Wavelet Multiresolution Inf Process, 2008, 6(1): 121-136.

[12] VENKATESAN N E. Spline-like wavelet filterbanks for multiresolution analysis of graph-structured data[J]. IEEE Transaction on Signal and Information Processing Over Networks, 2015, 1(4): 268-277.

[13] SUDEEP D T, JAYA H D, SHWETALI S E. Proposing self mutation of hybrid wavelet transform with Cosine Kekre Cosine-Sine & Cosine-Walsh for image compression[J]. IEEE International conference on futuristic trend in Computational analysis and knowledge management, 2015, 8(13): 2404-2412.

[14] YUAN Ying-jun, HUANG Zhi-tao, WU Hao. Specific emitter identification based on Hilbert–Huang transform based time frequency energy distribution feature[J]. The Institution of Engineering and Technology, 2014, 8(13): 2404-2412.

[15] GADDE A, ORTEGA A. A probabilistic interpretation of sampling theory of graph signals[J]. IEEE International Conference on Acoustic, Speech and Signal Processing, 2015, 9(10): 3257-3261.

编 辑 税 红

A Construction Method of Interpolatory Wavelet Based on Scaling Function

ZHANG Zhi-guo, HU Xue-hai, and ZHOU Yi

(School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 611731)

In classical wavelet sampling theory, interpolatory wavelets are constructed by using orthogonal wavelets. Since the analytic expressions of orthogonal wavelets are usually complex or unavailable, interpolatory wavelet construction has become an important topic in signal processing and harmonic analysis. In this paper, a new method is proposed to construct interpolating wavelets from scaling functions. Since this method has avoided using orthogonal wavelets in construction of interpolation wavelets, it can greatly improve efficiency of interpolating wavelet construction. Taking Daubechies and Coiflets MRAs as examples, our method is verified to be effective for interpolatory wavelet construction.

interpolatory bases; interpolatory wavelet; multiresolution analysis; wavelet sampling

TN911.97

A

10.3969/j.issn.1001-0548.2017.04.001

2016-05-31；

2016-12-26

国家自然科学基金(60904072,71301018)

张治国(1977-)，男，高级工程师，主要从事小波分析及神经网络建模方面的研究.