具有各向异性螺旋相位分布的椭圆光在各向同性介质中的传输特性

王玉青，钟东洲，张昕，黄东



具有各向异性螺旋相位分布的椭圆光在各向同性介质中的传输特性

王玉青，钟东洲，张昕，黄东

（五邑大学 信息工程学院，广东 江门 529020）

利用变分法和哈密顿法研究了具有各向异性螺旋相位分布的椭圆光在各向同性介质中的传输特性. 各向异性螺旋相位参数（拓扑指数）决定螺旋光的旋转特性，时光束的相位梯度在沿角向均匀（非均匀）分布，椭圆光的两半轴的旋转速度相同（不相同）. 利用哈密顿法理论计算了时的螺旋椭圆光稳定旋转传输满足的临界功率条件，且数值模拟结果也表明，在线性和非线性均为各向同性的非局域材料中，螺旋椭圆光能够在临界功率处稳定旋转传输，且旋转方向由拓扑指数的正负决定，即时螺旋光束沿逆时针（顺时针）旋转.

非线性光学；非局域非线性薛定谔方程；哈密顿法；椭圆光；各向异性螺旋相位

众所周知，衍射效应使得空间光束在均匀的线性介质中传输时发散，光束被展宽，由衍射所引起的束宽的变化率与束宽的平方成反比[1-2]. 即对于非对称的光束，长轴方向束宽的变化率比短轴方向的变化率更慢（衍射各向异性），因此，均匀的线性各向同性介质中只有圆形光束才能稳定传输，椭圆光不能保持其椭圆度不变，随着传播距离的增加，传输足够远距离后终将演变为圆形光束. 当线性衍射效应和非线性自聚焦效应达到平衡时，空间光束即能保持稳定不变的传输，此即空间光孤子[3]. 线性和非线性均为各向同性的介质中不可能存在非对称轴分布的椭圆形光孤子，只能存在圆形光束的稳定传输，这几乎是一个“毋庸置疑”的基本事实，因为椭圆光束在长轴和短轴方向上的束宽衍射不同，经历周期性的振荡，其无法形成稳定的光孤子传输[4]. 同时，文献[5]表明只有当衍射效应各向同性而非线性自聚焦效应为各向异性时，才存在稳定传输的椭圆光孤子. 然而，2010年Desyatnikov A.S.等[6]的研究工作打破了这一传统观念，他们预言交叉相位的椭圆光束（携带初始轨道角动量）可以在线性和非线性均为各向同性的饱和非线性介质中稳定传输. 随后Liang Guo等[7]也发现交叉相位的椭圆光束能够在线性和非线性均为各向同性的非局域非线性介质中保持椭圆度不变的稳定旋转传输，这是因为轨道角动量可导致等效的各向异性衍射，使得总衍射为各向同性，从而使椭圆光能在各向同性介质中稳定传输. 由此可见，光束的轨道角动量在衍射中占据重要地位，上述交叉相位的椭圆光束的相位为各向同性分布，但如果相位为各向异性螺旋分布时，同样可以引入轨道角动量，且文献[8]从理论上研究了非线性自聚焦克尔介质中各向异性螺旋相位分布的光束的传输特性，文献[9-10]也表明这种各向异性的螺旋相位可以用实验手段获得，并且指明这种类型的光束在选择性的边缘增强和探测方面发挥着重要作用. 那么，一个亟待解决的问题是：具有各向异性螺旋相位分布的椭圆高斯光束能否在线性衍射和非线性自聚焦效应均为各向同性的非局域介质中稳定传输？传输特性如何？本文将对此类光束在各向同性非局域介质中的传输特性进行详细研究.

1 传输模型

空间光束在无损耗的非局域非线性介质中传输时遵循非局域非线性薛定谔方程[3-5,7]：

， （2）

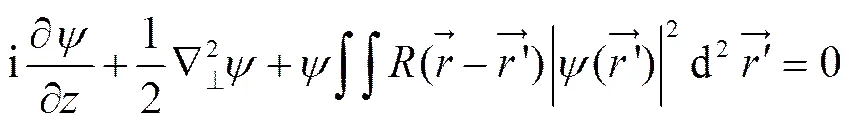
2 解析结果

本文假设试探解具有螺旋相位的椭圆高斯型分布[8]：

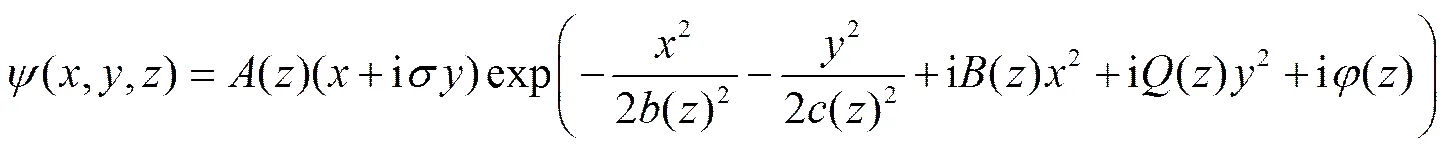
2.1 螺旋相位梯度对光束旋转速度的影响

如果椭圆光能保持其形状不变而稳定旋转传输，则长轴方向的旋转速度应和短轴方向的旋转速度相等，即其相位梯度应和方位角无关；否则，长轴和短轴的旋转速度不等将破坏原有的椭圆形状，无法形成椭圆光孤子，而只能以呼吸子形式存在. 涡旋相位的梯度为：

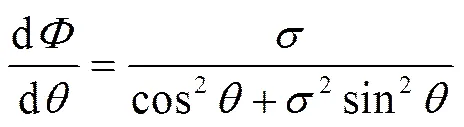
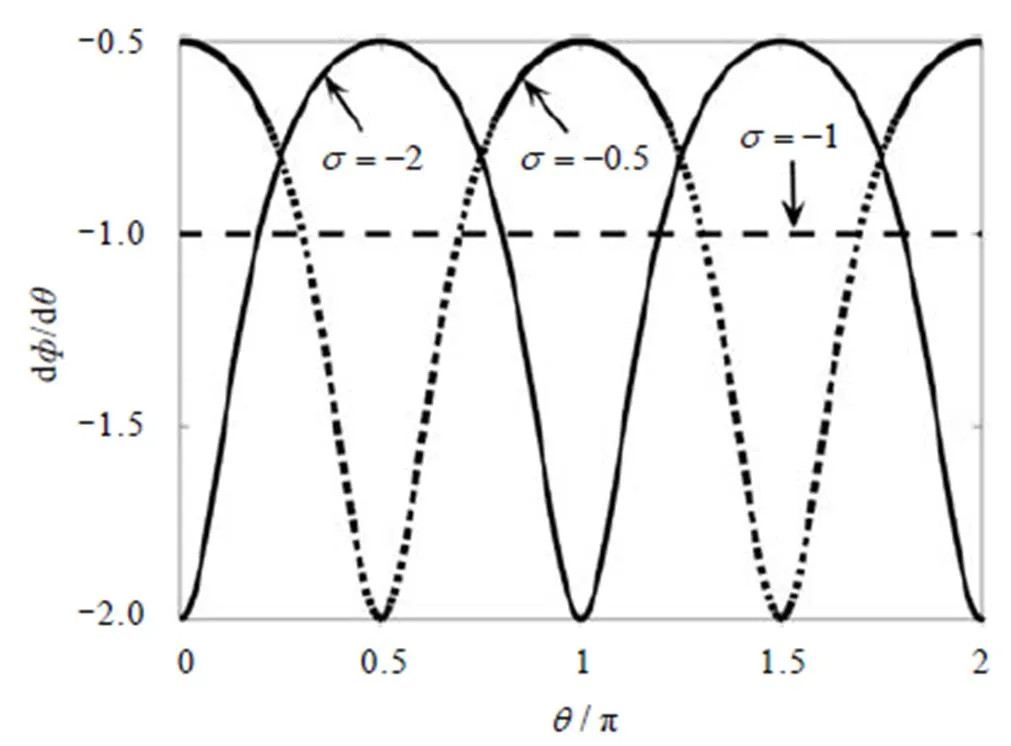
图1 不同时相位梯度随方位角的变化规律

2.2 变分法求解系统的哈密顿量

根据变分原理，方程（3）可由如下的拉格朗日密度函数描述[6-7]：

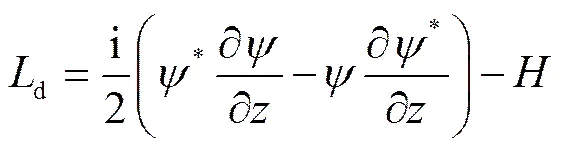
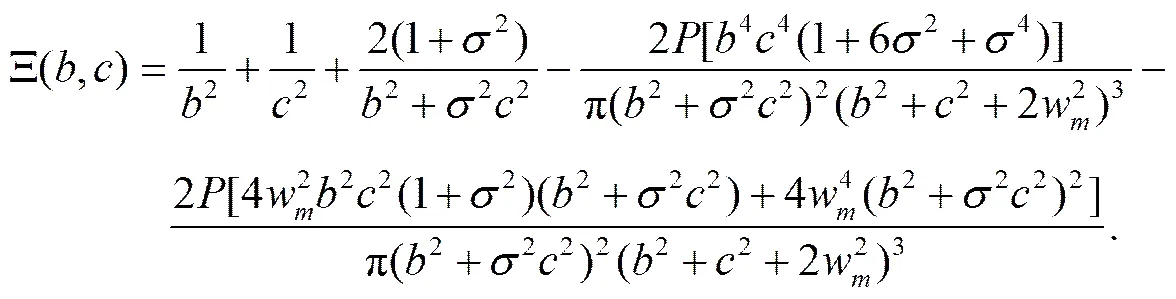
2.3 哈密顿法分析光束的稳定传输条件

不失一般性，假设螺旋椭圆光近似稳定旋转时长轴束宽近似保持不变，则有，可求得使半长轴近似保持不变的临界功率的表达式，进而求得此时振幅的表达式；但如果同时满足半短轴的宽度也近似不变，则需对临界功率（振幅）的表达式进行修正，取，只要系数取值合适，椭圆光的展宽效应和压缩效应可近似维持平衡，其以束缚态的形式在介质中旋转传输. 由可得临界功率：

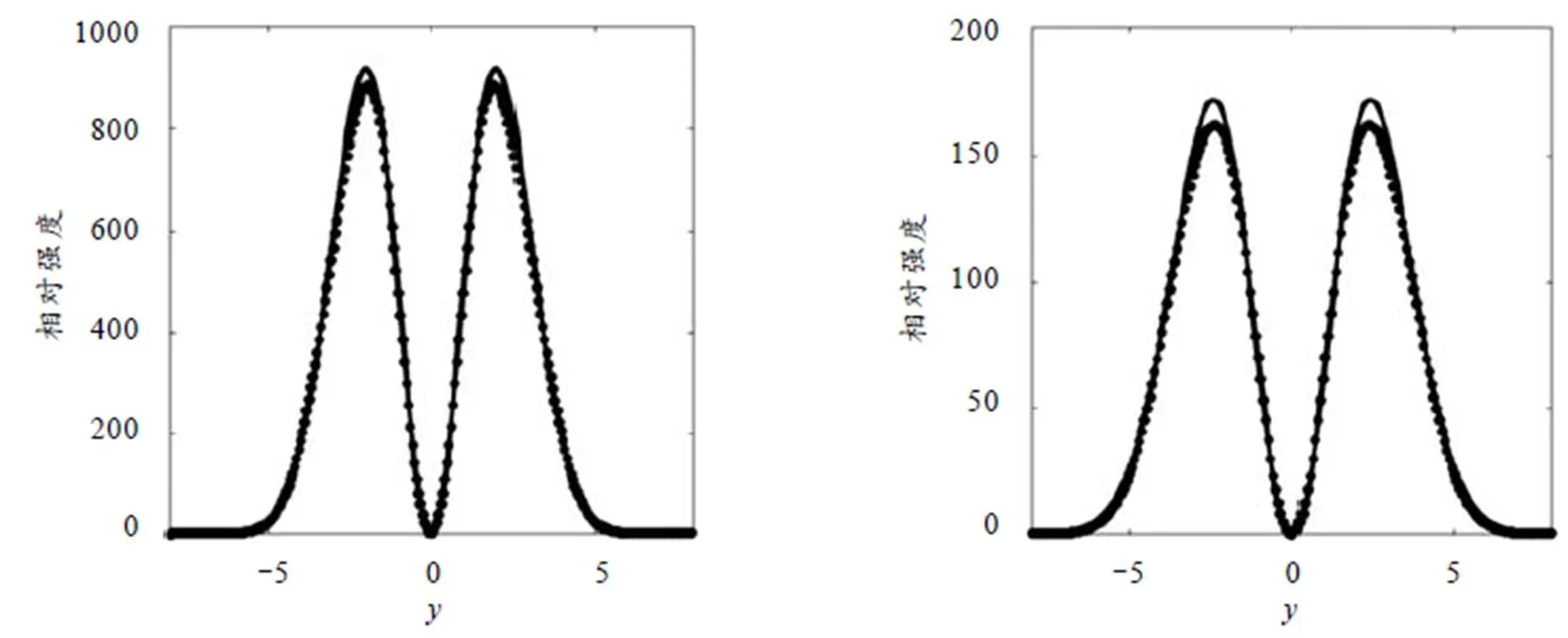
图2 ，，，时光束的传输图

从图2可知，初始输入为椭圆形，由于相位的各向异性导致半长轴和半短轴的旋转速度不同，初始时半长轴旋转速度较快，半短轴旋转速度较慢，故椭圆光在时已不能保持初始形状，光束已然发生分裂，且由图1可知，当半长轴旋转角度接近时速度将越来越慢，而此时半短轴旋转速度将越来越快，所以当光束传输到时，半长轴和半短轴均旋转了的角度；随着传输距离的增加，光束将沿着顺时针方向继续旋转，直到（已旋转了角度）时才恢复初始波形.

a. ，，， b. ，，，

改变初始条件，发现利用哈密顿法所得到的分析计算结果对不同输入情况的各向异性螺旋椭圆光同样适用.

3 结论

本文利用变分法和哈密顿法研究了具有各向异性螺旋相位分布的椭圆光在各向同性介质中的传输特性. 发现具有各向异性相位分布的螺旋椭圆光能够在线性各向同性和非线性各向同性的非局域材料中稳定旋转，而且光束的旋转方向与各向异性参数的正负有关，为正时光束逆时针旋转，为负时顺时针旋转；还发现时会导致相位梯度非均匀分布，进而影响椭圆光束两半长轴的旋转速度不同. 本文利用哈密顿法计算了螺旋椭圆光稳定旋转传输时所满足的功率条件，发现仿真模拟结果和解析计算结果吻合得较好. 本文所得结果有望在选择性边缘增强和探测方面发挥重要作用.

[1] CHEN Zhixiao, GUO Qi. Rotation of elliptic optical beams in anisotropic media [J]. Opt Commun, 2011, 284(13): 3183-3191.

[2] GUO Qi, CHI Sien. Nonlinear light beam propagation in uniaxial crystals: nonlinear refractive index, self- trapping and self-focusing [J]. J Opt A: Pure Appl Opt, 2000, 2: 5-15.

[3] SNYDER A W, MITCHELL D J. Accessible solitons [J]. Science, 1997, 276(6): 1538-1541.

[4] 王形华，郭旗. 椭圆高斯光束在强非局域非线性介质中的传输特性[J]. 物理学报，2005，54(7):3183-3188.

[5] 秦晓娟，郭旗，胡巍，等. 椭圆强非局域空间光孤子[J]. 物理学报，2006, 55(3): 1237-1243.

[6] DESYATNIKOV A S, BUCCOLIERO D, DENNIS M R, et al. Suppression of collapse for spiraling elliptic solitons [J]. Phys Rev Lett, 2010, 104(5): 1-4.

[7] LIANG Guo, GUO Qi. Spiraling elliptic solitons in nonlocal nonlinear media without anisotropy [J]. Phys Rev A, 2013, 88(4): 1-6.

[8] KIM G H, LEE H J, KIM J, et al. Propagation dynamics of optical vortices with anisotropic phase profiles [J]. J Opt Soc Am B, 2003, 20(2): 351-359.

[9] SHARMA M K, JOSEPH J, SENTHILKUMARAN P. Selective edge enhancement using anisotropic vortex filter [J]. Applied Optics, 2011, 50(27): 5279-5286.

[10] SITU Guohai, PEDRINI G, OSTEN W. Spiral phase filtering and orientation-selective edge detection/ enhancement [J]. J Opt Soc Am A, 2009, 26(8): 1788-1797.

[责任编辑：熊玉涛]

Propagation Dynamics of Elliptic Beams in Isotropic Media with Anisotropic Spiraling Phase Profiles

WANGYu-qing, ZHONGDong-zhou, ZHANGXin, HUANGDong

(School of Information Engineering, Wuyi University, Jiangmen 529020, China)

This paper investigates the propagation dynamics of spiraling elliptic beams (SEB) in isotropic media with anisotropic spiral phase distribution via the variational method and the Hamilton method. It is observed that the rotational behavior of SEB is determined by the anisotropic phase parameter (topological charge). When, the phase gradient is uniform (nonuniform), thus the rotation rates of the half axes of the SEB are equal (not equal) to each other. The critical powerof the steady rotating SEB is also obtained by the use of the Hamilton method for. Under the condition of input power, it is also found that, the steady rotating SEB withexist in the nonlocal media when the linear diffraction and the nonlinear self-defocusing are isotropic. It is found that the rotation direction of SEB is determined by the sign of topological charges. The positive (negative) sign ofcorresponds to the right-handed (left-handed) circulation.

nonlinear optics; nonlocal nonlinear Schrödinger equation; Hamilton method; elliptic beams; anisotropic spiraling phase

1006-7302（2017）03-0049-07

O437.5

A

2017-02-28

五邑大学青年基金资助项目（2014zk08）

王玉青（1982—），女，河南临颍人，讲师，在读博士生，主要从事非线性光学传输方面的研究.