双圈图的Wiener极性指数

胡云云，欧见平



双圈图的Wiener极性指数

胡云云，欧见平

（五邑大学 数学与计算科学学院，广东 江门 529020）

连通图的Wiener极性指数是它的距离等于3的点对数，通过引入图变换，本文确定了双圈图的极小Wiener极性指数，并刻画了极图. 两个圈点不交的双圈极图也得到了刻画.

双圈图；Wiener极性指数；Wiener指数

1 引言与预备知识

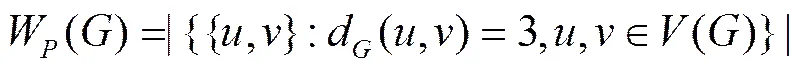
1998年，Lukovits和Linert[2]应用Wiener极性指数定量论证了许多含圈和不含圈的碳氢化合物的结构性质关系. Hosoya发现了Wiener极性指数的一个物理化学解释[3]. 文献[4]得到了Wiener极性指数和Zagreb指数之间的关系，同时确定了前两个具有最小的Wiener极性指数的单圈图，文献[5]确定了树的最小和最大Wiener极性指数，文献[6]确定了含个悬挂点的树的最大Wiener极性指数，并刻画了极图. 在文献[7-8]中，作者研究了单圈图和六角系统的Wiener极性指数，并刻画了极图. 本文确定了双圈图的极小Wiener极性指数，并刻画了极图，同时也研究了点不交的双圈图的极小Wiener极性指数，并刻画了极图.

2 图变换及其性质

引理1[10]若树含个顶点，则，等号成立当且仅当；如果则，等号成立当且仅当，其中且.

，

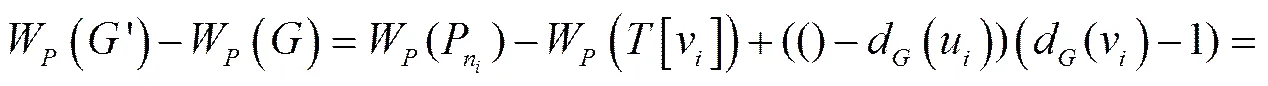
. （1）

.

，

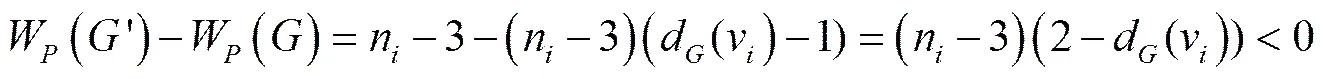
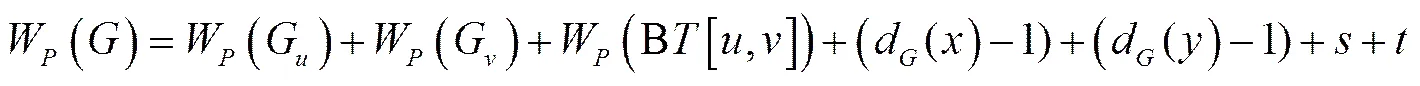
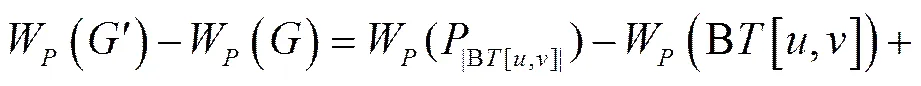
3 最小Wiener极性指数及极图

为了确定圈不交的双圈图的最小Wiener极性指数，我们还要引进一些其他的符号和术语. 用表示含有顶点，最大度为的单圈图的集合. 设是一个圈，. 先在点上连接个孤立顶点，. 然后，将一个星图的一个1度点与重合，这颗星有个顶点，得到的图记为，其中表示此图的点数；或者将个孤立点连接在上，得到的图记作；或者将的一个邻点的度为2的1度点与重合，得到的图记为. 易见，对所有成立；第二种情形下，；其他两种情形下. 而且，，或者，或者对某个成立. 参考下列图1.

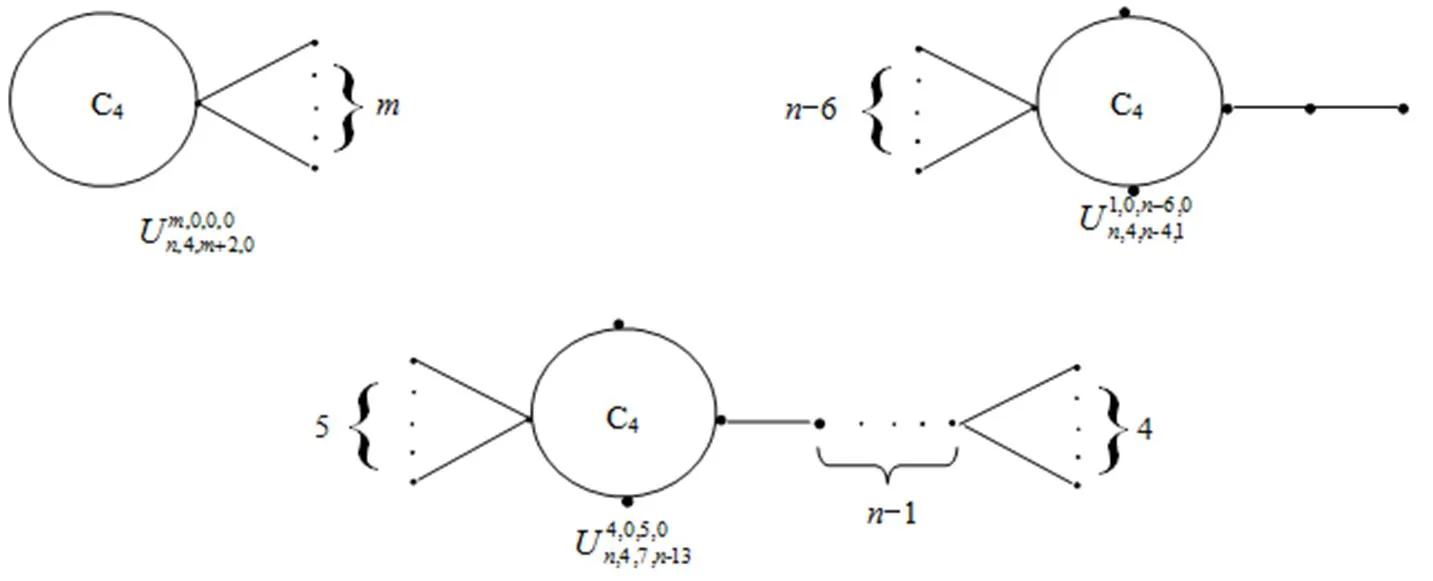
图1 几个特殊图

引理4[4]298如果是一个阶的单圈图，那么，等号成立当且仅当.

引理5[4]302设是一个阶的单圈图. 如果，那么，等号成立当且仅当.

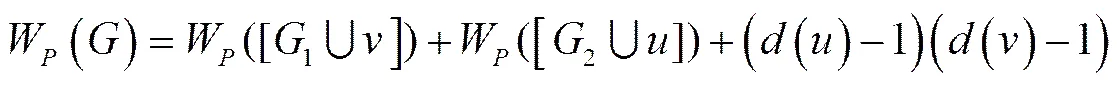
. （3）

.

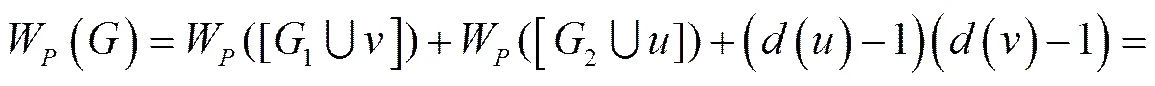
引理成立. 证毕.

，

.

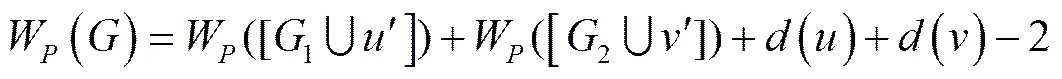
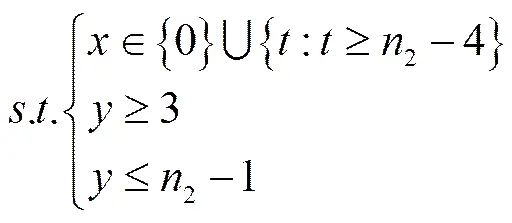
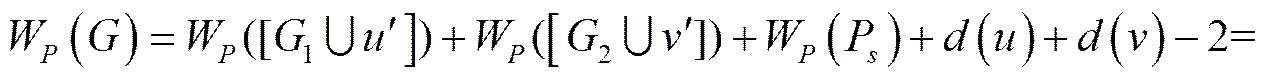
证毕.

证明 根据引理6和引理7，定理显然成立. 证毕.

[1] WIENNER H. Structural determination of paraffin boiling points [J]. Amer Chem Soc, 1947, 69(1): 17-20.

[2] LUKOVITS I，LINERT W. Polarity-numbers of cycle-containing structures [J]. Chem Inform Comput Sci, 1947, 38(4): 715-719.

[3] ROUVRAY D H, KING R B. Topology in chemistry-discrete mathematics of molecules [M]. [S.l.]: Horwood Pub, 2002.

[4] LIU Muhuo, LIU Bolian. On the Wiener polarity index [J]. MATCH Commun Math Comput Chem, 2011, 66(1): 293-304.

[5] DU Wenxue, LI Xueliang, SHI Yongtang. Algorithms and extremal problem on Wiener polarity index [J]. MATCH Commun Math Comput Chem, 2009, 62(1): 235-244.

[6] DENG Hanyuan, XIAO Hui. The maximum Wiener polarity index of trees withpendants [J]. App Math Lett, 2010, 23(6): 710-715.

[7] BEHMARAMA A, YOUSEFI-AZARI H, ASHRAFI A R. Wiener polarity index of fullerenes and hexagonal systems [J]. App Math Lett, 2012, 25(10): 1510-1513.

[8] HOU Huoquan, LIU Bolian, HUANG Yufen. The maximum Wiener polarity index of unicyclic graphs [J]. Appl Math Comput, 2012, 218(20): 10149-10157.

[9] BANDY J B A, MURTY U S R. Graph theory [M]. London: Springer, 2008.

[10] LIU Bolian, HOU Huoquan, HUANG Yufen. On the Wiener polarity index of trees with maximum degree or given number of leaves [J]. Comput Math Appl, 2010, 60(7): 2053-2057.

[责任编辑：韦 韬]

On Minimum Wiener Polarity Index of Bicyclic Graphs

HUYun-yun, OUJian-ping

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

The Wiener polarity index of a connected graphis defined as the distance being logarithm points of 3. By introducing some graph transformations, this paper determines the minimum Wiener polarity index of bicyclic graphs and characterizes the corresponding extremal graphs. Extremal bicyclic graphs with two cycles being vertex-disjoint are also characterized.

bicyclic graphs; Wiener polarity indexes; Wiener indexes

1006-7302（2017）03-0008-05

O157.5

A

2017-03-27

广东省自然科学基金资助项目（2014A030310413）

胡云云（1990—）女，江西南昌人，在读硕士生，主要从事图的边连通性研究；欧见平，教授，博士，硕士生导师，通信作者，主要研究方向为图论及其应用.