海浪破碎对北太平洋海表面温度模拟的影响

刘子龙, 史 剑, 蒋国荣



海浪破碎对北太平洋海表面温度模拟的影响

刘子龙, 史 剑, 蒋国荣

(解放军理工大学气象海洋学院, 江苏南京211101)

基于海浪模式WAVEWATCH III模拟北太平洋海浪要素, 结合NDBC浮标资料进行验证, 发现模拟出的有效波高与浮标测量值具有很好的一致性。基于改进型白冠覆盖率耗散模型, 利用海浪模式模拟出的有效波高、有效波周期和摩擦速度等海浪要素计算出单位面积水柱内因海浪破碎产生的湍动能通量。通过改变环流模式sbPOM湍动能方程的上边界条件, 引入海浪破碎产生的湍动能通量, 并探究海浪破碎对北太平洋海表面温度模拟的影响。研究表明, 由于海浪破碎的引入, 环流模式sbPOM对北太平洋海表面温度模拟的准确程度得到提升, 这为大气模式提供一个准确的北太平洋下边界条件具有重要意义。

海浪破碎; 海表面温度; WAVEWATCH III; sbPOM

近年来, 随着对上层海洋和低层大气物理过程耦合研究的不断深入, 对海浪运动的研究也得到了前所未有的关注, 所关注的焦点并非海浪现象本身, 而是海浪对其他海洋动力过程的影响[1]。海浪运动导致海洋上层混合的机制主要有: 波致雷诺应力引发的湍流混合、波浪破碎诱导的湍流混合、Stocks漂与风驱动的剪切流相互作用形成的Langmuir环流混合等[2]。本文在前人研究的基础上, 仅从海浪破碎诱导的湍流混合对海洋表面温度模拟产生的影响方面展开研究。

海浪是存在于海-气界面上的一种重要的运动形式, 海浪破碎对海洋上混合层中的湍流生成及其混合有着直接的影响。大量实验观测结果表明[3-5], 海浪破碎将促进海洋上混合层中湍流生成, 加强湍流垂向混合, 其影响深度与海浪成长状态有关。Toba等[6]根据观测指出海浪破碎的影响深度可达5倍有效波高。Thomson等[27]在数值模式中引入波浪破碎导致的湍动能通量, 发现波浪破碎的影响深度与垂直参考系相关。Alari等[20]基于耦合环流模式NEMO和海浪模式WAM引入海浪破碎作用, 发现海浪破碎对海表面温度、温度的垂直分布和上升流都产生较大影响。Breivik等[28]基于NEMO环流模式, 讨论了海表应力、波浪破碎导致的湍动能通量和Stokes Coriolis应力对混合层的影响, 发现3个物理过程对减小海表面温度偏差起到了巨大作用。管长龙等[1]总结前人所得, 认为波浪破碎为海表附近的湍流生成源, 在混合层上部形成一个影响磁层, 该层中的湍流耗散率分布不再遵从固壁定律所规定的结果, 波浪破碎的影响深度可达5~10倍有效波高。孙群等[8-10]为了研究海浪破碎对混合层中湍能量收支的影响, 采用垂向一维湍封闭混合模型, 通过改变湍动能方程的上边界条件, 引入海浪破碎产生的湍动能通量, 发现海浪破碎在海表产生的湍动能通量影响了海洋上混合层中的各项湍能量收支间的局部平衡关系。Sun等[11]利用M-Y一维湍封闭模型, 通过将波浪破碎作为海表湍流源引入, 发现考虑波浪破碎效应后, 模式模拟的海表面温度比未考虑波浪破碎效应时降低, 同时, 混合层深度增加, 模拟效果更显著。

为了探究海浪破碎效应在较大范围内对海表面温度的影响, 本文在采用先进的并行版本sbPOM环流模式[12]的基础上, 区别于孙群等[8]利用海浪模式WAM计算海浪破碎导致能量耗散率的方式, 利用Guan等[7]总结计算出的基于白冠破碎的能量耗散率表达式, 通过改变环流模式sbPOM湍动能方程的上边界条件, 引入海浪破碎产生的湍动能通量, 探究海浪破碎对北太平洋海域不同季节的海表面温度(Sea Surface Temperature, SST)的影响。

1 研究方法

1.1 WAVEWATCH III海浪模式简介及设置

WAVEWATCH III海浪模式(以下简称 WW3)是基于第三代海浪模式WAM发展起来的当前国际上最为成熟的几个海浪模式之一[13], 具有稳定性好、计算精度高等特点, 目前已成为美国海洋环境预报中心的业务化海浪预报模式。大量海浪数值模拟研究表明[14-16], WW3能够模拟出精度较高的海浪要素。

本文采用NCEP(National Centers for Environmental Prediction)再分析风场数据驱动WW3海浪模式(该数据空间分辨率为1.875°×1.9°, 时间间隔为6 h),模式地形数据由全球分辨率5′×5′的ETOPO5地形插值得到。模拟了2014年全年的北太平洋海域海浪过程。设置WW3模式考虑风摄入波动、非线性的波波相互作用、白帽耗散和底摩擦等物理过程, 相应的检验参数采用默认值。WW3模拟的区域范围为: 10°S~ 66°N, 100°~280°E, 空间分辨率为5°×5°。海浪谱频率分布范围为 0.041 8~0.41 Hz, 共分25个频段, 谱空间上离散为24个波向, 方向角分辨率为15°。模式最大全局时间积分步长取为2 400 s,方向和-theta方向最大CFL时间积分步长设为1 200 s, 最小源函数项时间积分步长本文中设为300 s。

1.2 sbPOM环流模式简介及设置

sbPOM(stony brook parallel ocean model)模式[12]是基于POM(princeton ocean model)模式[25]进行改进得到的一种可并行运算的环流模式, 刘欣等[17]曾采用区域海-气耦合模式WRF-sbPOM, 对理想热带气旋和海洋暖涡间的海气相互作用进行模拟, 获得较好的模拟效果。刘子龙等[26]曾在环流模式sbPOM中引入海浪搅拌混合作用, 并探究其对北太平洋海表面温度模拟的影响, 发现海浪搅拌混合作用的引入能够较大的改善原模式对北太平洋海表面温度的模拟。sbPOM除将POM改为并行外, 物理模型较原来无较大变化, 垂向坐标仍然采用坐标。本文关注的湍动能方程,

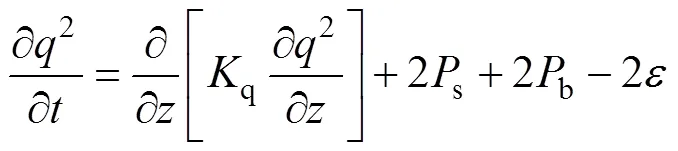
(2)

其中q为湍流垂向扩散系数;s、b和分别表示湍动能的剪切生成项、浮力生成项和耗散率;为湍流速度尺度;1为常数;为海水中的摩擦速度。

在对北太平洋海表面温度进行模拟的过程中, sbPOM模式空间分辨率与上文WW3模式设置保持一致, 垂向采用40个层, 在海洋上层采用较高的分辨率, 而在中、深层分辨率较低。模式初始温、盐场取自SODA资料月平均温度和盐度, 全场运动速度取零, 地形同样由全球分辨率为5′×5′的ETOPO5地形插值得到。风场和热通量取自空间分辨率为1.875°×1.9°的NCEP再分析资料中心, sbPOM模式外模时间步长为20 s, 内模时间步长600 s, 积分2 a, 取第二年积分结果进行分析。

1.3 海浪破碎的引入

海浪破碎能够在海表面产生湍动能通量, 进而影响海洋上混合层湍能量收支的平衡关系。近年来, 大量实验观测[18-19]也都证明海浪破碎对上混合层中湍能量收支有着重要的影响。因此海洋混合层模式中需要考虑海浪破碎的影响。

根据文献[21-22], 当考虑波浪破碎对海表面温度的影响时, 将在海表形成一向下输入的湍动能通量, 此时, 可将(2)式给定的海表边界条件改为(3)式:

结合Guan等[7]提出的改进型白冠覆盖率耗散模型,

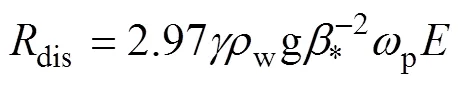
2 结果分析

2.1 海浪模式数值试验结果分析

选取模式模拟有效波高作为探究WW3海浪数值试验模拟结果准确性的验证要素。基于美国国家浮标资料中心NDBC(National Data Buoy Center), 选取如图1所示的8个浮标站数据进行验证, 验证的月份分别为2014年2月、5月、8月、11月。

限于篇幅, 图2仅给出了46075号浮标站点的4个月份的有效波高模拟结果和浮标测量结果的对比图。从图中可以看出, WW3海浪模式模拟有效波高值和浮标测量值具有很好的一致性, 但是在一些风速较大、变化较剧烈的时间段, 模拟结果稍不理想, 如, 2月8日到2月15日期间, 模式模拟结果和浮标测量结果存在一定偏差, 出现这种现象的原因可能是NCEP再分析风场资料时空分辨率不够高。

对图1所示8个浮标站点的模式模拟有效波高和浮标测量有效波高进行统计分析, 分别计算出均方根相对误差与相关系数, 其表达式分别如(6)、(7)所示。对于浮标因某些异常原因而未能进行测量或测量数据较少的月份, 在表1中用“NaN”表示。

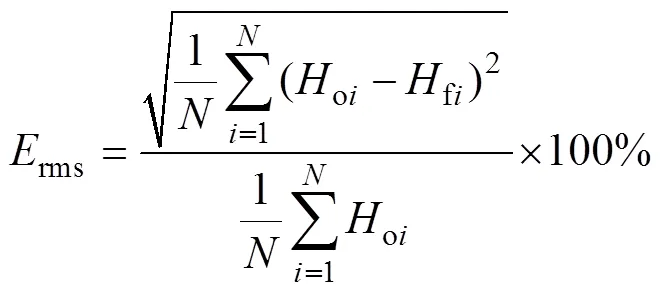
(6)

式中,o和f分别代表有效波高的浮标测量值和模式模拟值,为样本点的个数。

表1 模拟有效波高值的误差分析

Tab.1 Error analysis of the simulation significant wave heights

根据表1中8个浮标4个月份的模式模拟有效波高和浮标测量有效波高的均方根相对误差和相关系数的统计结果, 4个月份的平均均方根相对误差和平均相关系数差别不大, 其中2月份平均均方根相对误差较其他月份稍大, 为22%, 平均相关系数相对稍小, 为0.83。整体上, 模式模拟有效波高和浮标测量有效波高的均方根相对误差基本控制在20%左右, 最小仅为16%; 关系数基本控制在0.80以上, 最大相关系数为0.92, 且相关系数在0.80以下的仅有两个。

基于对图2和表1的分析结果, 可以得出, NCEP再分析风场资料可以作为WW3海浪模式的驱动风场, 其模拟出来的北太平洋有效波高等海浪要素准确度较高。

2.2 环流模式数值试验结果分析

图3分别给出了4个月份的未考虑海浪破碎模拟月平均SST和ECMWF(european center for medium range weather forecasts)再分析月平均SST之差在北太平洋的空间分布图。从图中可以得出, 在未引入海浪破碎的情况下, 环流模式sbPOM已经能够较为准确的模拟出北太平洋的海表面温度。在空间尺度上, 环流模式sbPOM对北太平洋中心海区模拟效果较好, 误差范围基本控制在±1℃左右, 而对近大陆海区模拟效果较差, 误差范围在±3℃左右。赤道地区多呈现模拟SST较ECMWF再分析SST偏低的趋势。在时间尺度上, 2月份和11月份北太平洋西部海区, 亚洲东岸邻近海区呈现模拟SST较ECMWF再分析SST偏高的趋势, 5月份和8月份北太平洋东部海区, 美洲西岸邻近海区呈现模拟SST较ECMWF再分析SST偏低的趋势, 且赤道地区西部海区常年呈现出模拟SST较ECMWF再分析SST偏高的趋势, 赤道地区东部海区常年呈现出模拟SST较ECMWF再分析SST偏低的趋势。

为初步了解海浪破碎不同月份对北太平洋海表面的作用情况, 图4给出了海浪破碎导致的湍动能通量在北太平洋不同月份的月平均空间分布图。从图中可以看出, 在时间尺度上, 2月份和11月份海浪破碎导致的湍动能通量较大, 而5月份和8月份海浪破碎导致的湍动能通量较小; 在空间尺度上, 中高纬度地区海浪破碎导致的湍动能通量较大, 而在低纬度地区导致的湍动能通量较小。

选取美国全球海洋数据同化实验室(USA Global Ocean Data Assimilation Experiment, USGODAE) 2014年2月27日如图5所示的9个浮标站点作为验证点, 将Argo浮标资料测量SST、未考虑海浪破碎模拟SST与考虑海浪破碎模拟SST的对比结果进行统计分析, 主要比较表中给出的绝对误差和相对误差, 其定义分别为:

(8)

自沉浮式剖面探测浮标又称Argo浮标, 因首先应用于国际Argo计划而被称为Argo浮标, 专门应用于海洋次表层温、盐、深剖面测量。Argo浮标每7 d或10 d浮出一次海面, 向卫星传输经度、纬度、深度、温度和盐度等资料, 然后再次潜入预定深度, 一般为2 000 m左右, 其经度、纬度、盐度和温度资料的精确度都为0.001。本文浮标测量SST数据取为Argo浮标测量首层海温数据, 其测量首层水深基本在5 m左右, 具体数据见表2。

根据表2的统计结果, 在sbPOM模式未引入海浪破碎时, 模式本身能够较为准确的模拟出北太平洋SST, 平均绝对误差仅为0.855。在模式引入海浪破碎后, 其模拟SST的平均值相比未引入海浪破碎时得到一定提升, 同时, 平均绝对误差由原来的0.855降为0.753, 平均相对误差由4.26%降到3.52%。综上所述, sbPOM模式在引入海浪破碎后, 北太平洋海域模拟SST的准确性将进一步提升。

3 讨论

为了能从整体上更加直观地了解波浪破碎对北太平洋海域不同季节海表面温度模拟的影响, 图6给出了4个月份北太平洋未考虑海浪破碎模拟SST和考虑海浪破碎后模拟SST之差分布图。

表2 SST北太平洋模拟与浮标实测的比较

Tab.2 Comparisons of the simulation SST with the results obtained from buoy data in the northern Pacific

注: “未考虑”表示未考虑海浪破碎; “考虑”表示考虑海浪破碎

对图6进行分析可以得出, 空间尺度上, 海浪破碎的引入, 对中高纬度SST模拟改善效果较为显著, 对低纬度海区SST模拟改善效果不明显; 对沿海地区改善效果比大洋内部及赤道地区效果明显。时间尺度上, 2月份和11月份海浪破碎的引入使得北太平洋大部分海区模拟SST比未引入波浪破碎时模拟SST减小, 以北太平洋西北海域最为明显; 而5月份和8月份北太平洋北部地区模拟SST主要呈现比未引入波浪破碎时模拟SST增大的趋势, 这也正好与图3得出的结论相对应: 未考虑海浪破碎时模拟SST比ECMWF再分析SST偏高地区, 如2月和11月份亚洲东部海区, 海浪破碎的引入, 使得模拟SST比未考虑海浪破碎时降低; 反之, 未考虑海浪破碎时模拟SST比ECMWF再分析SST偏低地区, 如5月和8月份北太平洋北部海区, 海浪破碎的引入, 使得模拟SST比未考虑海浪破碎时升高。结合图4可以发现, 海浪破碎导致的湍动能通量愈强的地区, 海浪破碎对北太平洋SST模拟的改善效果愈明显, 主要表现为使得海区模拟SST较未引入波浪破碎时减小, 而对于某些模拟SST较未引入波浪破碎时增大的海区, 如5月和8月份北太平洋北部海区, 从图4可以看出其海浪破碎导致的湍动能通量并不强, 其模拟SST的增大可能与海洋环流和海气热通量有关。一般情况下, 海洋环流模式在考虑海浪破碎后, 会增强海洋表层的混合, 通常使得SST降低, 但是海表面温度的升高或者降低同时还受到了海洋环流和海气热通量的影响[23 24], 这两个过程的作用都可能使得环流模式在加入海浪破碎后模拟的SST较原来偏大。通过对比可以发现, 在sbPOM模式对北太平洋SST进行模拟的过程中, 海浪破碎的引入使得海洋表面混合更加均匀, 模式模拟出来的SST更加准确。

4 结论

本文在WW3-sbPOM联合模型的基础上, 利用NCEP再分析风场驱动WW3海浪模式模拟出的有效波高、有效波周期和摩擦速度等海浪要素, 结合Guan等[7]提出的改进型白冠覆盖率耗散模型, 计算出海浪破碎导致湍动能通量。通过改变环流模式sbPOM湍动能方程的上边界条件, 引入海浪破碎产生的湍动能通量, 探究海浪破碎对北太平洋SST模拟的影响。研究表明: (1)在未考虑海浪破碎的情况下, sbPOM模式已经能够较为准确的模拟出北太平洋SST, 且对大洋中部模拟效果较好, 误差在±1℃左右, 对沿岸地区以及赤道地区模拟效果较差, 最大绝对误差可达±3℃左右。(2)从空间尺度上来说, 海浪破碎的引入, 对中高纬度SST模拟效果改善较大, 对低纬度SST模拟效果改善较小。从时间尺度上来说, 海浪破碎的引入, 使得2月份和11月份北太平洋大部分海区SST比未引入海浪破碎时模拟的SST减小, 而5月份和8月份北太平洋北部地区主要呈现出比未引入海浪破碎时模拟SST升高的趋势。(3)sbPOM环流模式中海浪破碎的引入, 使得海表面混合更加均匀, 对北太平洋SST的模拟相对于未引入海浪破碎之前有较大幅度提高, 模拟效果更好。

[1] 管长龙, 张文清, 朱冬琳, 等. 上层海洋中浪致混合研究评述——研究进展及存在问题[J]. 中国海洋大学学报自然科学版, 2014, 44(10): 20-24. Guan Changlong, Zhang Wenqing, Zhu Donglin, et al. Review of research on surface wave induced mixing in upper ocean layer: progress and existing problems[J]. Periodical of Ocean University of China, 2014, 44(10): 20-24.

[2] 张书文, 曹瑞雪, 朱风芹. 波浪破碎湍流混合研究综述[J]. 物理学报, 2011, 60(11): 786-791. Zhang Shuwen, Cao Ruixue, Zhu Fengqin. A review of the turbulent mixing by wind wave breaking[J]. Acta Physica Sinica, 2011, 60(11): 786-791.

[3] Kitaigorodskii S A, Lumley J L. Wave-turbulence interactions in the upper ocean. Part I: the energy balance of the interacting fields of surface wind waves and wind-induced three-dimensional turbulence[J]. Journal of Physical Oceanography, 1983, 13(11): 1977-1987.

[4] Terray E A, Donelan M A, Agrawal Y C, et al. Estimates of kinetic energy dissipation under breaking waves[J]. Journal of Physical Oceanography, 1996, 26(5): 792-807.

[5] Agrawal Y C, Terray E A, Donelan M A, et al. Enhanced dissipation of kinetic energy beneath surface waves[J]. Nature, 1992, 359(6392): 219-220.

[6] Toba Y, Kawamura H. Wind-wave coupled downward-bursting boundary layer (DBBL) beneath the sea surface[J]. Journal of Oceanography, 1996, 52(4): 409- 419.

[7] Guan Changlong, Hu Wei, Sun Jian, et al. The whitecap coverage model from breaking dissipation parametrizations of wind waves[J]. Journal of Geophysical Research, 2007, 112(112): 395-412.

[8] 孙群. 海浪破碎对海洋上混合层影响的数值研究[D]. 青岛: 中国海洋大学, 2003. Sun Qun. Numerical investigation of the effect of wave breaking on ocean surface mixed layer[D]. Qingdao: Ocean University of China, 2003.

[9] 孙群, 管长龙, 宋金宝. 海浪破碎对海洋上混合层中湍能量收支的影响[J]. 海洋与湖沼, 2006, 37(1): 69- 74. Sun Qun, Guan Changlong, Song Jinbao. Effect of wave breaking on turbulent energy budgets in ocean surface mixed layer[J]. Chinese Journal of Oceanology and Limnology, 2006, 37(1): 69-74.

[10] Sun Qun, Guan Changlong, Song Jinbao. Wave breaking on turbulent energy budget in the ocean surface mixed layer[J]. Chinese Journal of Oceanology and Limnology, 2008, 26(1): 9-13.

[11] Sun Qun, Song Jinbao, Guan Changlong. Simulation of the ocean surface mixed layer under the wave breaking[J]. Acta Oceanologica Sinica, 2005, 24(3): 9-15.

[12] Jordi A, Wang D P. sbPOM: A parallel implementation of Princenton Ocean Model[J]. Environmental Modelling & Software, 2012, 38(6): 59-61.

[13] Tolman H L. A thrid-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents[J]. Journal of Physical Oceanography, 1991, 21(6): 782-797.

[14] 张洪生, 辜俊波, 王海龙, 等. 利用WAVEWATCH和SWAN嵌套计算珠江口附近海域的风浪场[J]. 热带海洋学报, 2013, 32(1): 8-17. Zhang Hongsheng, Gu Junbo, Wang Hailong, et al. Simulating wind wave field near the Pearl River Estuary with SWAN nested in WAVEWATCH[J]. Journal of Tropical Oceanography, 2013, 32(1): 8-17.

[15] Wang Jizhao, Zhang Jie, Yang Jungang. Numerical simulation and preliminary analysis on ocean waves during Typhoon Nesat in South China Sea and adjacent areas[J]. Chinese Journal of Oceanology & Limnology, 2014, 32(3): 665-680.

[16] Cui Hong, He Hailun, Liu Xiaohui, et al. Effect of oceanic current on typhoon-wave modeling in the East China Sea[J]. Chinese Physics B, 2012, 21(10): 592-599.

[17] 刘欣, 韦骏. 热带气旋与海洋暖涡间的海-气相互作用[J]. 北京大学学报(自然科学版), 2014, 50(3): 456- 466. Liu Xin, Wei Jun. Air-Sea interaction between Tropical Cyclone and Ocean Warm Core Ring[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(3): 456-466.

[18] Agrawal Y C, Terray E A, Donelan M A, et al. Enhanced dissipation of kinetic energy beneath surface waves[J]. Nature, 1992, 359(6392): 219-220.

[19] Terray E A, Donelan M A, Agrawal Y C, et al. Estimates of kinetic energy dissipation under breaking waves[J]. Journal of Physical Oceanography, 1996, 26(5): 792-807.

[20] Alari V, Staneva J, Øyvind Breivik, et al. Surface wave effects on water temperature in the Baltic Sea: simulations with the coupled NEMO-WAM model[J]. Ocean Dynamics, 2016, 66(8): 917-930.

[21] Mellor G L, Yamada T. A hierarchy of turbulence closure models for planetary boundary layers.[J]. Journal of the Atmospheric Sciences, 1974, 31(7): 1791-1806.

[22] Mellor G L, Yamada T. Development of a turbulence closure model for geophysical fluid problems[J]. Reviews of Geophysics and Space Physics, 1982, 20(4): 851-875.

[23] 宋振亚, 乔方利, 杨永增, 等. 波致混合对热带太平洋海气耦合模式中冷舌模拟的改进[J]. 自然科学进展, 2006, 16(9): 1138-1145. Song Zhenya, Qiao Fangli, Yang Yongzeng, et al. The improvement of wave-induced mixing on the simulation of cold tongue in the tropical Pacific Ocean with sea-air coupled model[J]. Progress in Natural Science, 2006, 16(9): 1138-1145.

[24] 宋振亚, 乔方利, 雷晓燕, 等. 大气-海浪-海洋环流耦合数值模式的建立及北太平洋SST模拟[J]. 水动力学研究与进展, 2007, 22(5): 543-548. Song Zhenya, Qiao Fangli, Lei Xiaoyan, et al. The establishment of an atmosphere-wave-ocean circulation coupled numerical model and its application in the North Pacific SST simulation[J]. Journal of Hydrodynamics, 2007, 22(5): 543-548.

[25] Blumberg A F, Mellor G L. A description of a three dimensional coastal ocean circulation model[C]// Heaps N S. Three-Dimensional Coastal Ocean Models, vol 4. Washington DC: American Geophysical Union, 1987: 1-16.

[26] 刘子龙, 史剑, 蒋国荣, 等. 海浪搅拌混合对北太平洋海表面温度模拟的影响[J]. 海洋科学, 2016, 40(12): 131-137. Liu Zilong, Shi Jian, Jiang Guorong, et al.Influence of wave-induced mixing on a sea surface temperature simulation of the North Pacific[J]. Marine Sciences, 2016, 40(12)131-137.

[27] Thomson J, Schwendeman M S, Zippel S F, et al. Wave breaking turbulence in the ocean surface layer[J]. Journal of Physical Oceanography, 2016, 46(6): 1866- 1882.

[28] Breivik Ø, Mogensen K, Bidlot J, et al. Surface wave effects in the NEMO ocean model: Forced and coupled experiments[J]. Journal of Geophysical Research Oceans, 2015, 120(4): 135-143.

(本文编辑: 刘珊珊)

Effect of wave breaking on the sea surface temperature simulation in the North Pacific

LIU Zi-long, SHI Jian, JIANG Guo-rong

(College of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101, China)

In this paper, wave parameters in the North Pacific were simulated by the WAVEWATCH III and were combined with NDBC buoy data verification. We found that the simulated significant wave height is highly precise. Based on the modified model of whitecap coverage dissipation, turbulence kinetic energy (TKE) fluxes due to wave breaking were calculated using the simulated significant wave height, wave period, and friction velocity. The influence of surface wave breaking could be introduced into ocean model sbPOM by modifying the existing surface boundary condition of the TKE equation and specifying its input. The effects of wave breaking on the SST simulation in the North Pacific were also investigated. The results indicated that wave breaking can improve the accuracy of the ocean model sbPOM on the North Pacific sea surface temperature simulation and it plays an important role in providing accurate lower boundary conditions in atmospheric models.

wave breaking; sea surface temperature; WAVEWATCH III; sbPOM

Sep.4, 2016

[National Natural Science Foundation of China, No.41676014]

P732.7

A

1000-3096(2017)03-0122-08

10.11759/hykx20160904001

2016-09-04;

2017-01-18

国家自然科学基金项目(41676014)

刘子龙(1991-), 男, 湖南常德人, 硕士研究生, 研究方向: 海洋动力学与数值模拟, 手机: 18761683583, E-mail: 941117242@qq.com; 史剑(1981-), 通信作者, 男, 江苏扬州人, 副教授, 研究方向: 海洋动力学与数值模拟, 手机: 13813388338