基于启发式搜索代价的多查询结果分类方法
2017-10-13高建
高 建
基于启发式搜索代价的多查询结果分类方法
高 建
(盘锦职业技术学院 机电工程系,辽宁盘锦124010)
提出了一种基于搜索代价的对Web数据库多查询结果进行分类的方法,该方法首先通过分析用户的查询习惯,构建一个通用的查询结果分类树探测模型,然后根据探测模型建立分类树的搜索代价模型。对于搜索代价,提出了基于查询历史的搜索代价估计方法。最后,以降低搜索代价为目标在查询结果集上生成一个分类树,用户通过检查该分类树上各分支节点的标签来逐步定位到其感兴趣的信息。实验及分析表明,本文所提方法能够有效避免信息过载,并且具有较好分类效果和较低搜索代价。
搜索代价;信息过载;查询结果分类
随着WWW的发展,以数据库为中心的Web应用越来越广泛。对于用户提交的查询,传统的查询处理技术只是简单地返回满足查询要求的查询结果。然而,对于蕴含海量数据的Web数据库来说,一个查询往往会产生大量的查询结果,也就是“信息过载”现象,信息过载发生在用户不确定他搜寻什么[1]。这种情况下,用户开始通常会提出一个普通的、选择性较弱的查询,以便将所有可能需求的结果包含进来。对查询结果进行分类和排序是处理信息过载的2种互补的技术。通过分类或排序,用户通常会重新形成一个更具选择性的查询。所以,分类和排序并非直接有用,其作用在于协助用户形成更为明确的查询条件。现有研究工作提出的查询分类是预先生成一个目录结构,目录中的分支标签也是预先指定好的,在查询的时候,查询结果被集成到预定义的目录结构中。由于这样的分类是独立于查询的,因此查询结果在目录中的分布会不均匀,一些目录下可能具有大量的结果元组,而另外一些目录下可能就具有少量的结果元组。
为了解决信息过载问题,本文提出一种对查询结果进行分类的方法。该方法根据元组内容对元组聚类,然后在查询结果集上生成一个带标签的分类树。该分类树是在查询进行过程中生成的,所以不会出现预分类问题。该方法通过鉴定分类空间开始,然后开发一个探测模型,这样用户可以跟着导航层次结构进行逐步细化查询。
1 相关工作
解决Web数据库信息过载的2种方法是对查询结果进行排序和分类。目前已经有大量工作对查询结果排序方法进行了研究,大致分成3类:第一类是利用用户相关反馈,用户通过在属性或元组上明确指定其偏好,然后系统根据用户反馈对查询结果排序[2-3];第二类是利用用户偏好描述文件对查询结果进行个性化排序,用户偏好文件由用户根据其偏好创建和更新[4-5];第三类是通过分析查询历史,推测隐式用户偏好,据此对查询结果进行排序[6-7]。查询历史记录了使用系统的所有用户提交的查询条件集合,在很大程度上能反映出用户的查询习惯和大多数用户的兴趣偏好,因此本文也利用查询历史来估计用户使用查询结果分类树进行搜索的代价。
近年来,已有一些工作研究信息检索结果[8]和文本文档[9-10]分类方法。但是,Web数据库查询的分类与信息检索和文本文档的分类不同,主要差别是数据库同时包含文本和数值,而信息检索的对象就是文本文档;另一方面,对查询结果分类既要考虑分类准确性还要考虑用户使用分类树的搜索代价,而文本分类只需考虑分类的准确性。
对于数据库查询结果的分类,只有文献[11]研究了关系数据库SQL查询结果的分类方法,该方法基于C4.5决策树算法,根据属性的信息增益确定分类树的分类属性,对数值型属性的区间划分采用二元划分方法。该方法虽然具有较低的搜索代价,但是存在以下不足:(1)查询结果元组只能在叶节点下查看,非叶子节点不能展开显示所包含的元组;(2)分类属性确定的依据是属性的信息增益,而信息增益反映的是属性划分数据的能力而并非降低搜索代价的能力;(3)数值区间划分的范围过大或过小,不能满足用户的现实需求。本文所提方法能够有效克服上述问题,因此具有较为重要的理论意义和应用价值。
2 分类基本概念
2.1 分类空间
令是一个元组集合(是一个基本表、一个视图、或者一个查询的结果集)。假设不包含任何聚合或派生的属性。的一个层次分类是一个基于属性和值对于在中元组的递归划分。图1给出了在yahoo房地产网站上搜索位置在西雅图市的房产查询结果分类树例子。
结合上例,描述查询结果分类的基本思想和相关概念。
分类树:给定分类结构的根(第0层),它包含所有在中的元组,使用一个属性将中的元组划分成为一个相互非重合的目录(第1层节点)。例如,图1中的根节点,根据属性“Neighborhood”将元组划分成3个分支,即
归纳步骤:给定一个在第-1层的节点,根据一个给定的属性递归划分包含在中的元组集合(),使其成为一个互不重叠的目录有序列表。使用的属性被称为第层节点的分类属性,也是第1层节点的子分类属性。例如,“Price”是在第2层中所有节点的分类属性,同时也是第1层所有节点的子分类属性。需要指出的是,一个属性只能有一次机会作为分类属性。
与每一个节点关联的是一个分类标签以及一个元组集,定义如下。
分类标签:标签()是对一个节点的描述。例如,图1中根的第一个孩子有标签“NeighborhoodÎ{Redmond,Bellevue}”,同时上述目录分支的第一个孩子有标签“Price: 200k-225k”。
元组集:包含在中的元组集(),称为的元组集合,该集合满足上的标签。换句话说,()是在中满足从根到路径上所有节点标签的元组子集。例如,在图1中对于带有标签“Neighborhood: Redmond, Bellevue”的目录,()是一个在中位于Redmond或Bellevue的房产集合。
由此可见,一个目录的标签,向用户明确描述了哪个元组在父节点的集合中。用户通过观察标签就能够决定是否去选择进一步展开的子目录。()有如下结构。
如果分类属性是一个文本型属性:()的形式为“Δ,其中Ì(),()表示属性在的值域。如果.Î,则元组满足标签()。
如果分类属性是一个数值型属性:()的形式为“1£<2”,其中1,2Î()。如果1£<2,则元组满足标签()。
根据上述层次分类结构,对于分类结构的每一个层次,需要进行如下操作。
(1)对于层次,确定其分类属性。
(2)对于第-1层的每一个分类,决定如何去划分()中的元组,使其在属性的值域上成为互不重叠的子集。
目标是选取在每一个层次上的属性-划分结合,使得查询结果分类树有最小的信息过载。
2.2 搜索模型
给定一个查询结果分类树,用户通常会以自顶向下或自左向右的方式检查该树的非叶子节点(或称中间节点)上的标签,然后逐步定位到其所需信息。假设用户现在位于节点(可以是根节点、中间节点或叶子节点),在该节点上操作如下。
(1)如果是一个非叶子节点,用户可以有2种方式探测目录:一是“显示元组”方式,即显示()中的所有元组;二是“显示子目录”方式,即显示下的所有子目录,如果下有个子目录,用户将检查这个子目录标签,然后选定其中某个子目录C进行探测,递归执行上述过程。
(2)如果是一个叶子节点,则只能进行“显示元组”操作,即显示()中的所有元组。
3 代价评估
3.1 代价模型
给定一个查询结果分类树,用户使用树以某种路径进行探测进而找到相关元组的代价用Cost(,)表示,该代价包含2个部分:一部分是用户检查中间节点标签的代价,另一部分是用户检查节点下元组的代价。一般情况下,用户查找相关元组的时间与用户需要检查的条目(包括中间节点的标签和节点下的元组)的总数呈正比,即用户需要检查的标签或元组数越多,在查找相关元组上花费的时间就越多,搜索代价就越高。
例如,计算在图1中分类树上的搜索代价Cost(,)。假设对于检查根节点的代价是0,分支“Price: 225k-250k”下包含20条元组,则搜索代价就是3(用于检查3个第一层目录的标签)+3(用于检查“Neighborhood: Redmond, Bellevue”子目录的3个标签)+20(用于检查在分支“Price:225k-250k”下的20条元组)=26。
在实际应用中,由于不能明确知道用户的查询意图,因而无法确定用户会选择哪个分支和哪些元组。为了对搜索代价进行估计,需要知道下列2个与中每个目录相关联的概率,从而估计Cost(,):
探测的概率:假设用户探测目录的概率为()。用户探测目录,是指用户在目录上进行了“显示元组”或“显示子目录”操作;相应地,用户忽略的概率是1-()。
“显示元组”的概率:假设用户探测目录,令用户使用“显示元组”方式探测目录的概率为P(),那么用户使用“显示子目录”方式探测的概率就是1-P()。如果是一个叶节点,则P()=1,因为该情况下“显示元组”是唯一的选项。
假设在上述概率已知的情况下,下面介绍如何计算Cost(,)。考虑分类树中的一个非叶子节点,令1,2, …,C是中的个子目录。如果用户对于节点选择了“显示元组”,则表明他检查在中的所有元组,因此代价就是|()|;如果用户对于节点选择了“显示子目录”操作,则总体代价就是检查下所有子目录标签的代价加上可能选择去探测下若干子目录的代价。对于第二种情况,代价模型中的第一个因数是*,其中是检查一个目录标签的代价,代表下的子目录总数;第二个因数是探测目录C的代价。因此,用户探测节点的搜索代价公式为:
Cost()=P()*|()|+
(1-P())**+(C)*(C)) (1)
如果是一个叶节点,()=|()|。注意,上述定义对于叶子节点,P()=1也成立。并且,当是根节点时,该代价就是分类树的搜索代价。
3.2 概率估计
本节讨论如何利用查询历史估计概率P()和(),从而估计分类树的搜索代价Cost()。
选择“显示元组”操作的概率:假设用户探测非叶子节点,有2个互斥的选择:“显示元组”和“显示子目录”。首先考虑用户探测选择“显示子目录”的概率,如果的子分类属性A能够使得用户仅仅对下少数子目录感兴趣,该情况下使用“显示子目录”可以使用户忽略大部分其他子目录,所以在很大程度上减少了用户需要检查的元组数量。另一方面,如果用户对下大部分或所有子目录感兴趣,即用户对A()中的大部分或所有的值感兴趣,则将选择“显示元组”操作。
本文采用查询历史作为评估P()和()值的依据,具体方法如下:在查询历史中,如果用户已在属性上指定了查询条件,表明用户对A中的一些值感兴趣;如果用户在A上没有指定查询条件,表明他对上的所有值都感兴趣。如果(A)表示查询历史中在属性A上包含查询条件的查询个数,表示查询历史中查询记录的总数;(A)/表示用户对属性A中的一些值感兴趣的比例。因此,一个用户对于A中的一些值感兴趣,即选择“显示子目录”操作的概率是(A)/,相应地对执行“显示元组”的概率P()就是1-(A)/。
探测目录的概率:探测目录的概率用()表示。探测目录是指用户根据上的标签来决定使用“显示元组”或“显示子目录”来探测目录的概率,或者说,()是在用户检查的标签条件下进一步选择探测的概率。
由于用户探测意味着用户已经检查了的标签,因此,()=(用户探测)/(用户检查的标签)。当且仅当用户探测的上级目录并且对执行showcat操作时,用户才可能去检查的标签,因此,
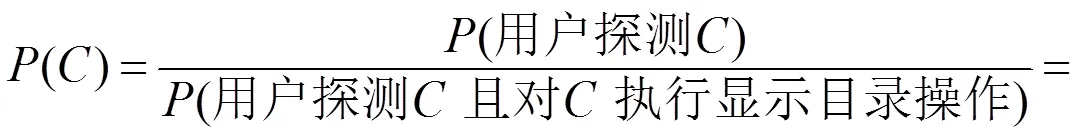
注意,上式中分母,即条件概率:
(对执行‘显示子目录’操作|用户探测)
实际上就是对执行‘显示子目录’操作的概率,即(A())/。
再考虑式(2)中的分子,概率:(用户探测),是用户对上标签感兴趣的概率,这个概率值可用查询历史中在的分类属性A上与()相重叠的查询条件个数来估计,即用N()/来计算,其中表示查询历史中查询的总数。
最后,()可以用下式来衡量:
()=N()/(A) (3)
其中,N()代表查询历史中在的分类属性A上与标签()相重叠的查询条件个数,(A)表示查询历史中在属性A上包含查询条件的查询个数。
4 分类算法
4.1 分类属性约简和属性划分
4.1.1 分类属性约简
在查询历史中,属性的出现次数()越低,用户对根节点执行“显示元组”操作的概率P()就越高。因为一个树的“显示元组”的代价通常要比“显示子目录”的代价高,一个高的“显示元组”概率意味着树的搜索代价将有一个较大的(P()*|()|)值。所以,在预处理阶段需要消除低出现频率的属性。在本文中,如果一个属性以小于的比例出现在查询历史中,即,()/<,消除。阈值由系统或专家指定。
4.1.2 文本型属性划分
分类树的构建需要对分类属性进行划分,即对分类属性下的值进行划分。
对于一个文本型分类属性,本文采用单值划分方法。例如,对于目录,如果它的子分类属性在()上包含个不同值{1,…,v},则将目录划分成个子分支目录,每个目录的标签对应这个不同的文本值。
为了降低搜索代价,首先统计每个文本值v在查询历史中出现的次数,记为(v),该值存放在知识库表中,其结构为{ID,文本值,出现次数}。
4.1.3 数值型属性划分
划分数值属性的基本思想是利用最佳分割点对数值属性的值域进行数值区间的划分。最佳分割点是查询历史中用户经常以某个数值开始或结束的查询数值点。假设要将属性的值域划分为个区间,则需要-1个分割点,这些分割点是查询历史中指定在属性上的大多数范围查询的起始点或结束点。
给定一个分割点,令b和e分别代表查询历史中以点开始或结束的查询条件的个数,把b和e相加作为点作为分割点的最终成绩,该成绩越大,则点越适合作为分割点。
4.2 查询结果分类树构建
本文以递归方式构建查询结果分类树,对于分类树的每一层,都需要处理以下两个问题。
(1)决定分类属性。
(2)对于在-1层的每一个目录,划分在()中属性的值域,使得信息过载最小化。
在本文中,当且仅当节点包含超过个元组,将对进一步划分,其中是一个给定的参数。查询结果分类树构建算法如下所示。

算法1. 查询结果分类树构建算法 Categorize(R)输入:查询结果R,参数M,数值区间分割点成绩输出:基于R的分类树T1. 创建一个根节点 (层次=0) 并且添加到T2. l =1; //把当前的层设置为13.while在第l-1 层存在至少一个目录,它的|tset(C)|>M时4. S¬{C | C是在l-1层的目录且|tset(C)|>M}5. for每一个分类属性A6. if A是一个文本属性7. SCL¬以occ(vi)的降序列出所有的单值目录8. for S中的每一个目录C9. 构建Tree(C, A),该树以C为根,以A上的每个文本值作为C的子目录10. else //A是一个数值型属性11. SPL¬按分割点对数值区间进行分割12. for S中的每一个目录C13. 构建Tree(C, A),该树以C为根,以A上划分的区间作为C的子目录14. 计算15. 选择作为第l层的分类属性16. for S中的每一个目录C17. 把由使用属性a得到的划分Tree(C, a)添加到T中18. l = l+119. end
算法1从第0层开始创建分类树,每层的分类属性都是从剩余属性中选取具有最小搜索代价的属性作为分类属性。算法递归执行,直到每个目录包含的元组个数不超过个为止。
5 实验及性能分析
5.1 实验环境
实验使用的机器配置为64位3.30 G处理器,8 G内存和500 G硬盘,操作系统为Windows 2007,算法采用Java语言实现。测试数据使用http://estate.yahoo.com的房地产销售数据库,选择Washington州的Seattle城市,元组数约有20 000条,包含的属性有Price、SqFt、Location、Bedrooms、Bathrooms、Buildyear、Garage、Livingarea、Neighborhood和Schooldistrict,其中Price、SqFt、Bedrooms、Bathrooms和Buildyear是数值型属性,其余为文本型属性。查询历史包含2 000条用户查询。
对比算法:将本文方法(简称Cost-based)与文献[11]方法(简称C4.5-based)进行对比,分别测试二者在实际搜索代价和平均搜索代价方面的效果。
5.2 分类效果测试
本文邀请10个用户,每个用户提出一个测试查询,对于每个测试查询,用户从查询结果中选出与其兴趣和偏好最为相关的部分元组。在此基础上测试分类树的分类效果。
(1)实际搜索代价
实际搜索代价不同于预计搜索代价,它是用户使用分类树找到所有相关元组而实际访问的条目(包括检查节点标签和元组)的代价总和。很明显用户通过检查越少的节点数和元组数就能找到所有相关元组,那么表明实际搜索代价越低,因此分类方法越好。表1给出了每个测试查询在2种分类方法下的实际搜索代价。
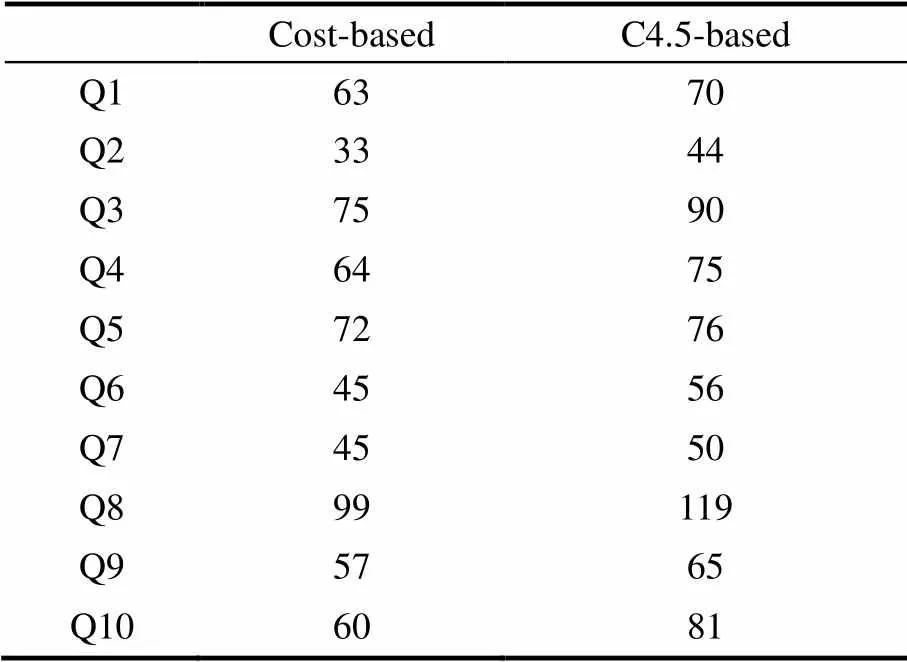
表1 不同分类方法的实际搜索代价对比
(2)平均搜索代价
仅对比实际搜索代价实际上并不公平,因为对于相同的测试查询使用不同的分类算法,用户通常会找到不同个数的相关元组,因此需要用实际搜索代价除以找到的相关元组数,也就是平均搜索代价来反映用户找到一个相关元组所需花费的代价。表2给出了对于每个测试查询利用上述2种分类方法的平均搜索代价对比。

表2 不同分类方法的平均搜索代价对比
通过上述比较可知,本文提出的分类效果优于文献[11]提出的方法,这是因为:(1)对于划分数值属性,本文采用了多元划分,即选取多个最佳分割点,使得分割后的每个区间都是用户在以往查询中经常指定的,因此降低了搜索代价,而文献[11]方法仅使用二元划分,不可避免地导致划分的区间过大或者过小,从而造成搜索代价的增加;(2)本文方法每层选取的分类属性是用户在查询历史中频繁指定的属性,因此会降低执行“显示元组”操作的概率,从而降低了搜索代价,而文献[11]方法是通过考察属性的信息增益来确定分类属性,然而信息增益的目的是用来划分数据而并非降低搜索代价;(3)本文方法在非叶子节点上能够进行“显示子目录”和“显示元组”操作,而文献[11]的方法只能在叶节点上显示元组。综上,本文方法在分类效果和搜索代价方面都优于现有方法。
6 结论与展望
提出了一种以降低搜索代价为目的的Web数据库查询结果分类方法,该方法在查询处理阶段根据查询结果动态生成一个分类树,用户通过检查节点标签来决定探测哪个分支。本文方法分成2个阶段,在离线阶段,根据查询历史计算用户探测某个分支的概率,包括“显示子目录”和“显示元组”的概率;在线处理阶段,在查询结果集上根据搜索代价选取分类属性,以递归方式生成查询结果分类树。实验结果表明,本文方法构建的查询结果分类树具有较低的搜索代价和较好的分类效果。
如何对分类树中的目录进行排序是需进一步解决的问题。
[1] Meng X F, Ma Z M, Yan L. Answering approximate queries over autonomous web databases[C]. Proceedings of the 18th International World Wide Web Conference, 2009, 1021-1030.
[2] Agarwal G, Mallick N, Turuvekere S. Ranking database queries with user feedback: a neural network approach[C]. Proceedings of the International Conference on Database Systems for Advanced Applications, 2008, 424-431.
[3] Wichterich M, Beecks C, Seidl T. Ranking multimedia databases via relevance feedback with history and foresight support[C]. Proceedings of the IEEE 24th International Conference on Data Engineering Workshop, 2008, 16-25.
[4] Santhanam G R,Basu S, Honavar V. Representing and reasoning with qualitative preferences for compositional systems[J]. Journal of Artificial Intelligence Research, 2011, 42(1): 211-274.
[5] Koutrika G, Ioannidis Y E. Personalized queries under a generalized preference model[C]. Proceedings of the International Conference on Data Engineering, 2005, 841-852.
[6] Coffman J, Weaver A C. Learning to rank results in relational keyword search[C]. Proceedings of the ACM Conference on Information and Knowledge Management, 2011, 1689-1698.
[7] 孟祥福, 马宗民, 李昕, 等. 基于上下文偏好的Web数据库查询结果Top-k排序方法[J]. 计算机学报, 2014, 37(9): 1986-1998.
[8] Liu T Y, Wan H, Ma W Y. An editor labeling model for training set expansion in web categorization[C]. Proceedings of the 2005 IEEE International Conference on Web Intelligence, 2005: 165-171.
[9] Bekkerman R, El-Yaniv R, Tishby N, Winter Y. Distributional word clusters vs words for text categorization[J]. Journal of Machine Learning Research, 2003, 3(3): 1183-1208.
[10] Al-Mubaid H, Umair S. A. A new text categorization technique using distributional clustering and learning logic[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(9): 1156-1165.
[11] Chen Z Y, Li T. Addressing diverse user preferences in SQL-Query-Result navigation[C]. Proceedings of the ACM SIGMOD International Conference on Management of Data, 2007: 641-652.
责任编校:孙 林
Categorization Approach to Query Results Based on Heuristic Searching Cost
GAO Jian
(Department of Mechanical and Electrical Engineering, Panjin Vocational & Technical college, Panjin 124010, China)
This paper proposes a categorization approach to query results based on searching cost. Firstly, a general exploration model which meets users’ query habits is presented. And then, a searching cost model is built corresponding to the exploration model. To estimate the searching cost, this paper proposes a searching cost measuring method by taking advantage of query history. Lastly, a labeled and leveled categorization tree is generated according to the searching cost. By using the categorization tree, users can easily find their favorite results by checking the label assigned on the tree nodes. The experiments demonstrate that the method can efficiently avoid the information overload, and has the higher categorization accuracy and lower searching cost as well.
searching cost; information overload; query result categorization
10.15916/j.issn1674-3261.2017.02.004
TP311
A
1674-3261(2017)02-0085-06
2016-06-22
高建(1981-),男,辽宁盘锦人,讲师,本科。
