混合型微分方程的加权伪概周期解

庄 严



混合型微分方程的加权伪概周期解

庄 严

（辽宁铁道职业技术学院铁道工程系辽宁锦州 121000）

研究了带有逐段常数变量的混合型微分方程的加权伪概周期解存在唯一性。首先针对具有强迫项的线性微分方程给出了加权伪概周期解存在唯一性的构造性证明，然后利用所得结果再结合不动点方法对非线性扰动方程给出了加权伪概周期解存在唯一性证明。

逐段常数变量；混合型微分方程；加权伪概周期解

1994年张传义[1]推广概周期函数的概念，定义了伪概周期函数，并研究了这类函数在微分方程理论中的应用。后来许多学者进一步研究了这类函数在许多不同类型的方程中的应用，得到了较丰富的成果，参见文献[2-3]及其中的参考文献。1999年，Yuan等[3]研究了带逐段常变量的混合型线性微分方程：

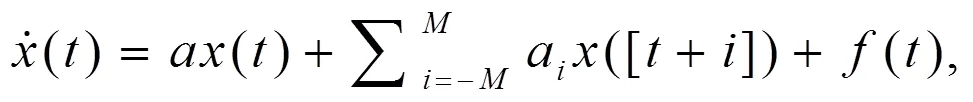
(1)

和相应的非线性方程：

(2)

的伪概周期解的存在唯一性问题。2006年，Diagana引进了比伪概周期函数更广泛的函数类，定义了加权伪概周期函数，并研究了这类函数在微分方程中的应用，参见文献[4-7]。本文的目的是当是加权伪概周期函数，而关于是一致加权伪概周期函数时，证明方程(1)和(2)的加权伪概周期解存在唯一性。

下面简要介绍一些记号和定义。

定义1[8]称是概周期的，如果对任意给定的，集合：在实轴上相对稠密，即对任意，存在，使得在每个长度为的区间内至少有一个，使得不等式对一切成立。所有这样的函数构成的集合记为。在上确界范数下构成Banach空间。

定义2[8]称关于是一致概周期函数，如果对任意与任给紧集，存在，使得在每个长度为的区间内至少有一个，使得不等式对一切成立。所有这样的函数构成的集合记为。

定义3[9]称序列为概周期序列，如果的—移位集：为上相对稠密集。用记这样序列的全体，其中是整数集。

定义4[1]称函数是伪概周期的，如果可表为，其中分别称和为的概周期部分和遍历扰动部分。

定义6[1]有界连续函数称为关于是一致伪概周期的，如果可表为：其中。分别称为一致伪概周期函数的概周期部分和遍历扰动部分

定义7[3]有界序列称为伪概周期序列，如果可表为：其中为概周期序列，满足：，分别称为的概周期部分和遍历扰动部分。设，即定义在上取值为实数的有界连续函数的全体，则按最大模范数下是一个Banach空间。

定义8[6]有界连续函数称为关于是一致权伪概周期的，如果可表为：其中。分别称为一致权伪概周期函数的概周期部分和遍历扰动部分。

引理1[6]任意一个权伪概周期函数的分解式是唯一的，且。因此：

引理2[8]在最大模范数下为一个Banach空间。

(3)

引理3[6]设满足Lipschitz条件：

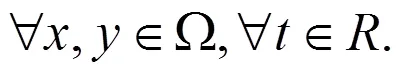
1 一些引理和主要结果

定义12[3]称函数是微分方程(1)（或(2)）的解，则它满足以一下3个条件：

,

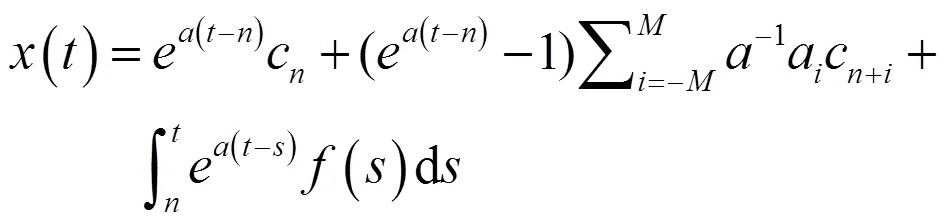
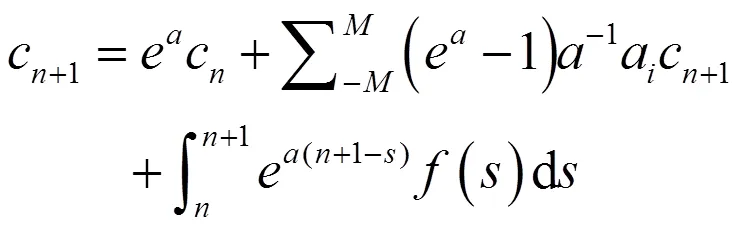
令：

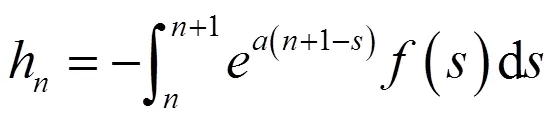
将上述等式代入方程（4），可得：

(6)

方程（6）对应的齐次方程为：

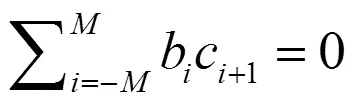
(8)

现在可以叙述本文的主要结果。

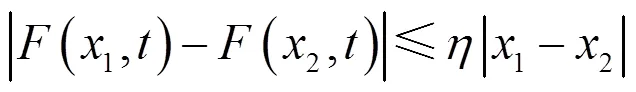
为了证明上述主要定理，需要如下几个引理。

引理4[3]如果是一个概周期函数，则序列：

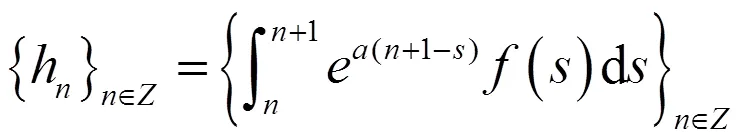
是一个概周期序列。

证明 由：

立即得到所需结论。

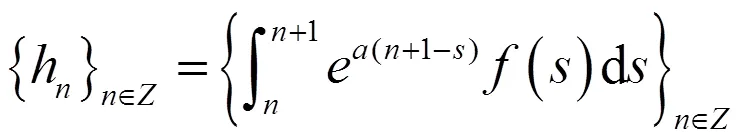
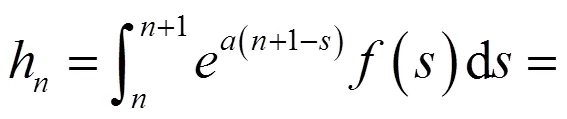
由引理4知：

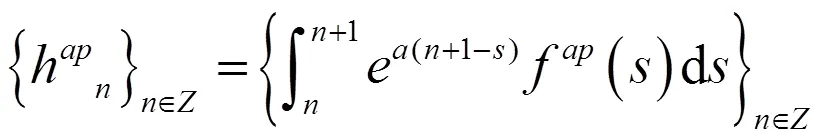
为概周期序列。另一方面：

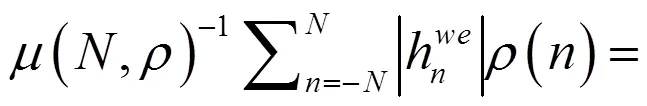
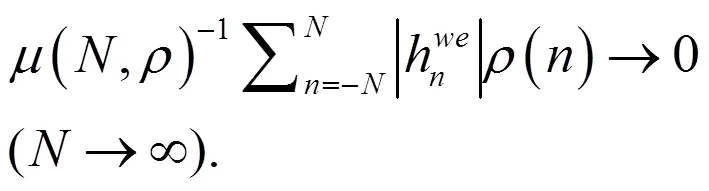
2 主要结果的证明

定理1的证明 方程（8）是齐次方程而且它的所有根均为单根，因此：

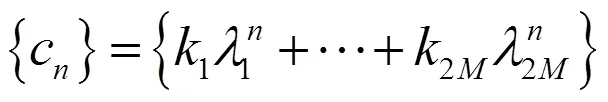
令：

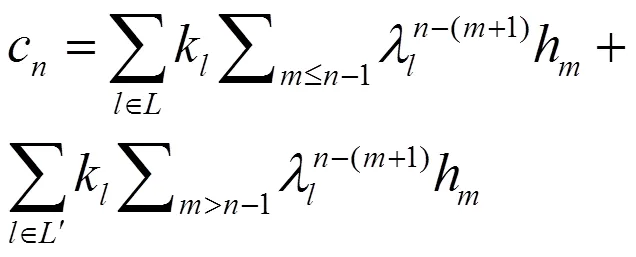
不失一般性，假设：

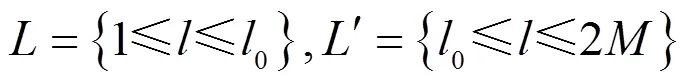
(10)

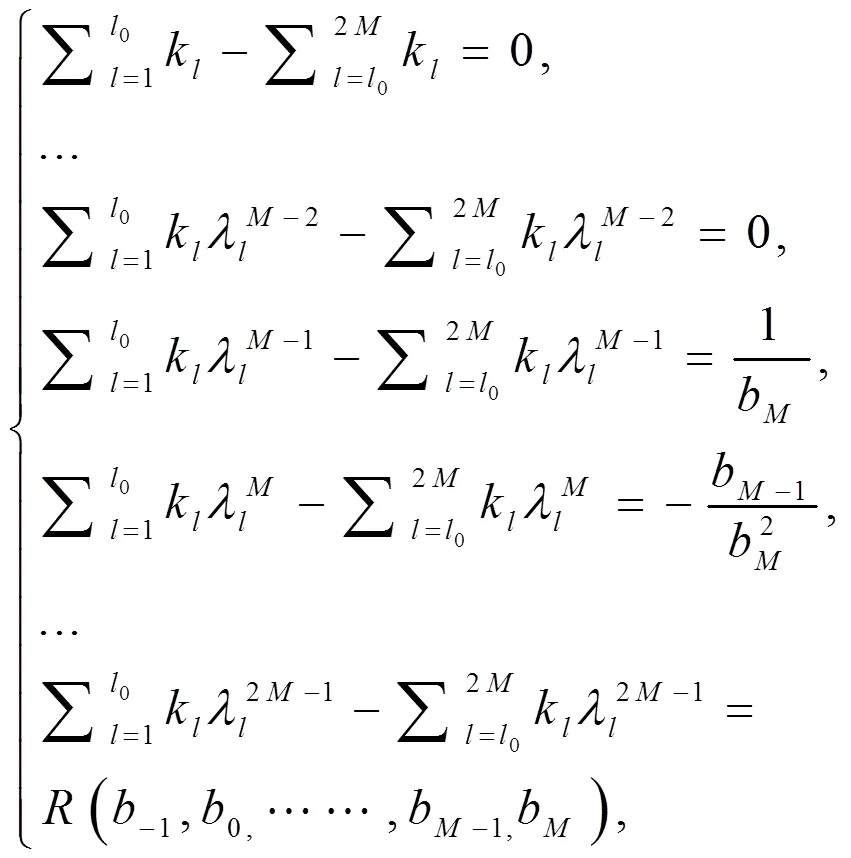
(12)

为差分方程（6）的一个解。

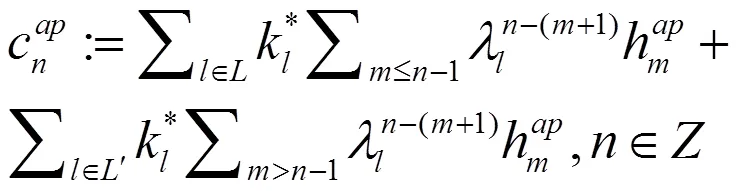
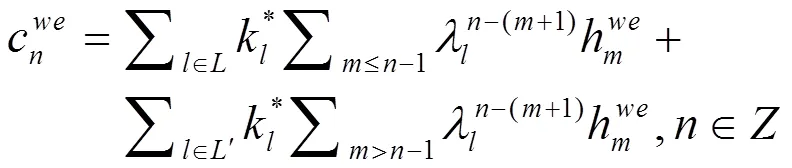
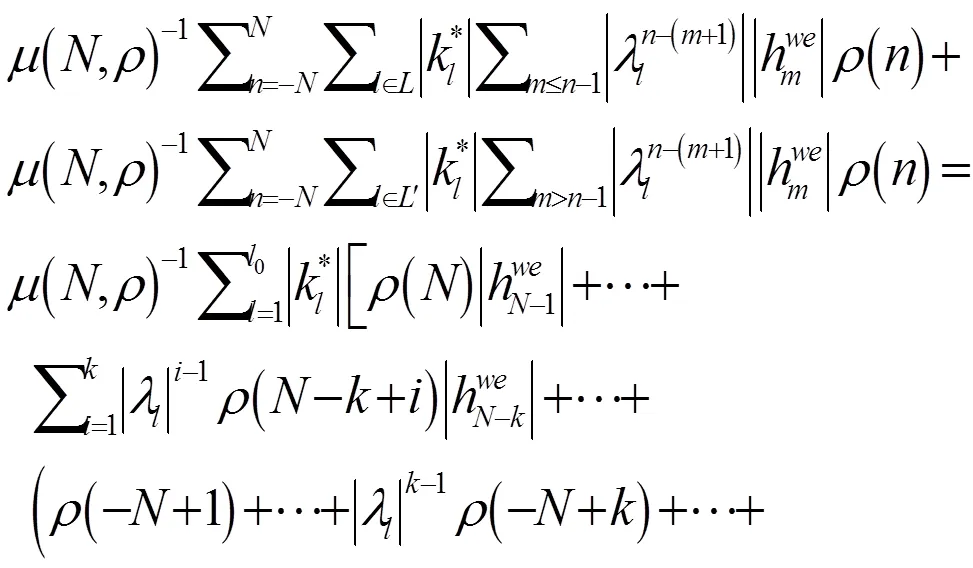
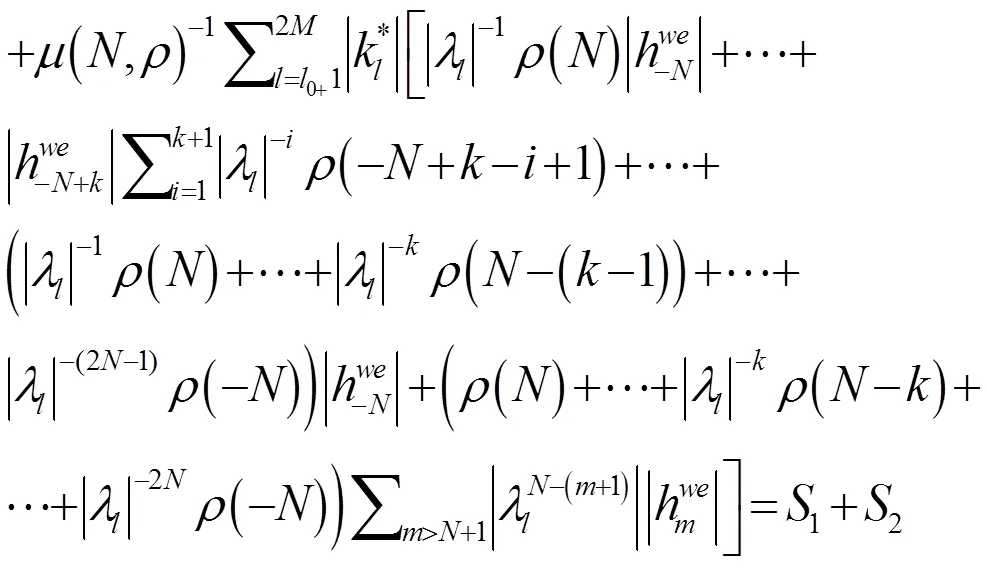
此时，易知（4）是微分方程（1）的1个解。

由文献[9]中定理1的证明可知：

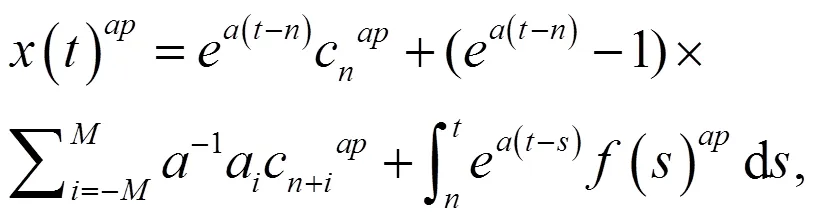
为概周期的，显然：

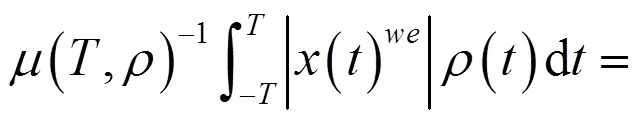
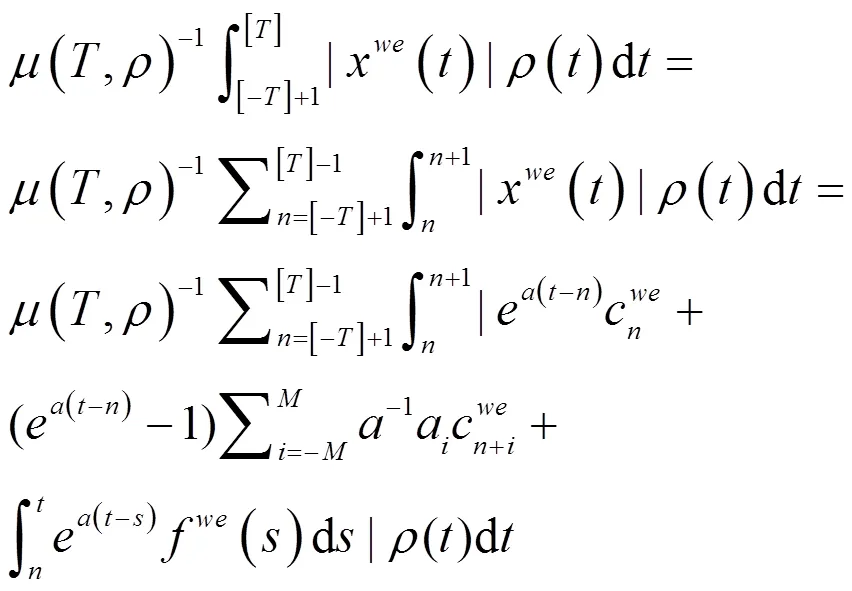
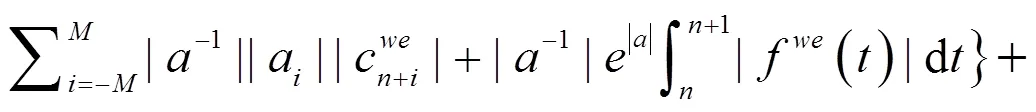
定理2的证明 用不动点方法证明这个定理。由定理1可知，对任意的，为一个权伪概周期函数。考虑方程：

(13)

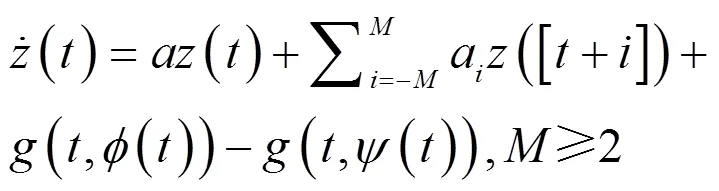
所以有：

其中：

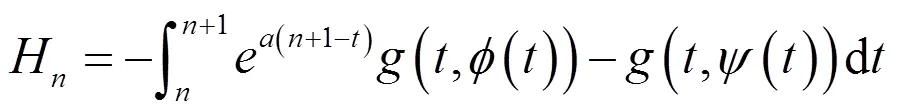
进而得到：

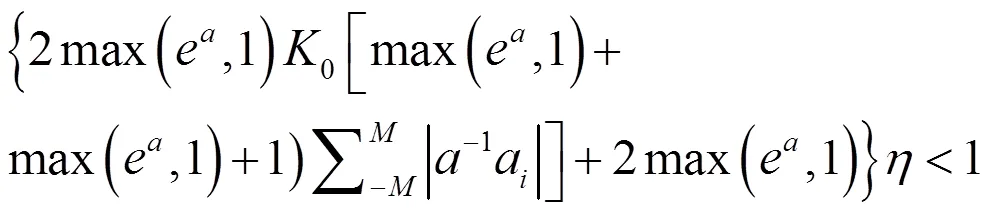
3 结束语

本文的结果说明，对于带有逐段常变量的混合型微分方程来而言，强迫项的属性决定了有界解的属性。当强迫项是加权伪概周期函数时，仍然能够得到唯一的加权伪概周期解。

[1] Zhang C, Pseudo almost periodic solutions of some differential equations[J]. J Math Anal Appl, 1994, 181: 62-76.

[2] Yuan R, Hong J. Almost periodic solutions of differential equations with piecewise constant argument[J]. Analysis, 1996, 16: 171-180.

[3] Yuan R, Piao D. Pseudo almost periodic solutions of differential equation with piecewise constants argument[J]. Applicable Analysis, 1999, 73(3-4): 345-357.

[4] Diagana T. Weighted pseudo-almost periodic functions and applications[J]. C R Acad Sci Paris, Ser I, 2006, 343(10): 643-646.

[5] Diagana T. Weighted pseudo-almost periodic solutions to some differential equations[J]. Nonlin Anal TAM, 2008, 68: 2250-2260.

[6] Diagana T. Existence of weighted pseudo almost periodic solutions to some classes of hyperbolic evolution equations[J]. J Math Anal Appl, 2009, 350: 18-28.

[7] Diagana T. Weighted pseudo-almost periodic solutions to a neutral dalay integral equation of advanced type[J]. Nonlin Anal TAM, 2009, 70: 298-304.

[8] 何崇佑, 概周期微分方程[M]. 北京: 高等教育出版社, 1992: 1-53.

[9] Fink A M. Almost periodic differential equations[M]. Lecture Notes in Mathematics, 1974.

责任编校：孙 林

Weighted Pseudo Almost Periodic Solutions to Mixed Type Differential Equation

ZHUANG Yan

（Department of Railway Engineering, Liaoning Railway Vocational and Technical College, Jinzhou 121000, China）

In this paper, we study the existence and uniqueness of weighted pseudo almost periodic solutions to mixed type differential equations with piecewise constant arguments. We provide a constructing proof for the existence and uniqueness of weighted pseudo almost periodic solutions for a linear equation with forced terms, and then using fixed point method we prove the existence and uniqueness of weighted pseudo almost periodic solutions for the nonlinear perturbed equations.

piecewise constant arguments; mixed type differential equations; weighted pseudo almost periodic solutions

10.15916/j.issn1674-3261.2017.02.003

O175.1

A

1674-3261(2017)02-0079-06

2015-11-11

山东省自然科学基金项目(ZR2013AM026)

庄严(1961-)，男(满族)，辽宁沈阳人，副教授，本科。