激发态在不对称分子谐波发射中的作用
2017-10-13冯立强
刘 航,冯立强
激发态在不对称分子谐波发射中的作用
刘 航1,冯立强2
(1.辽宁工业大学化学与环境工程学院,辽宁锦州 121001;2.辽宁工业大学理学院,辽宁锦州 121001)
理论研究了激发态效应在不对称分子LiH3+谐波发射过程中的作用。结果表明,由于激发态与基态之间的激光诱导电子跃迁过程,在低阶谐波处会出现谐波共振增强的现象。并且,通过计算不同分子核间距、激光频率、场强、相位、脉宽下的高次谐波谱图,发现激发态引起的激光诱导电子跃迁过程是普遍存在于不对称分子电离过程中的。
激发态;高次谐波;激光诱导电子跃迁
高次谐波作为研究原子、分子、晶体内部超快物理过程的强大工具,一直是研究的热点之一[1-3]。
原子、对称小分子体系谐波发射过程可以通过Corkum提出的“电离-加速-回碰”模型来解释[4]。这里电子的电离和再回碰都是发生在基态。但是,最近研究表明,对于一些存在固有偶极具的多中心不对称分子,例如HeH2+离子[5-6],不仅基态对谐波发射起作用,其激发态也对谐波发射起到一定作用。例如,Bian等[7]发现在HeH2+发射高次谐波的过程中其1sσ基态和2pσ激发态之间存在一个明显的激光诱导电子跃迁过程。Chen等[8]发现HeH2+发射高次谐波,其每一次谐波都是由基态和激发态共同贡献的结果。虽然HeH2+发射高次谐波的特点已经被一些研究学者研究过,但是目前还不确定这些特点是否广泛地存在于不对称分子当中。
因此,为了解决上述问题同时也是为了更好地理解电子在不对称分子中的运动过程,本文理论研究了LiH3+分子离子发射高次谐波的特点。
若无特殊说明,本文均采用原子单位。
1 理论模型
高次谐波研究可通过数值求解含时薛定谔方程得到,这里假设电子主要沿激光偏振方向振荡,在长度规范和电偶极近似下,方程可表示为[9]:
(1)
其中:

是LiH3+的软核库伦势,其中是分子间核间距。为电子波函数。激光场为:
(2)
其中、0、和分别表示激光振幅、频率、脉宽和相位。
高次谐波谱可以通过傅立叶变换偶极加速度得到:
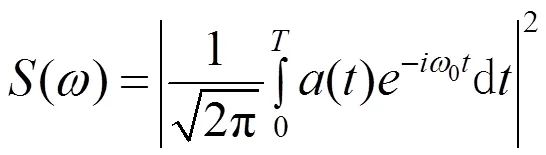
其中偶极加速度可以通过艾伦费斯特定律[10]获得:
(4)
2 结果与讨论
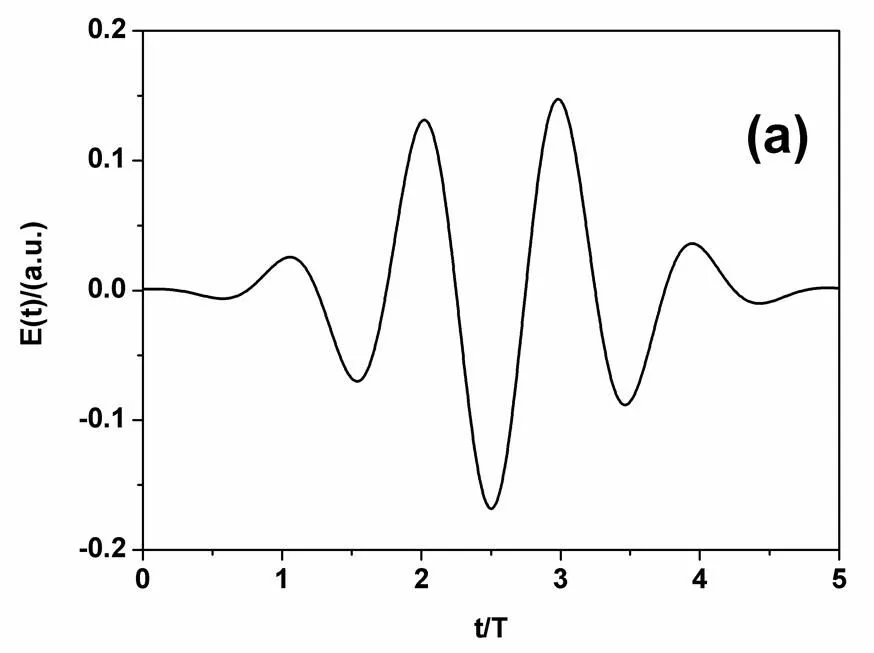
图1给出LiH3+分子离子在5 fs/800 nm激光场下发射谐波的特点。其中场强、相位以及核间距分别为=1.0×1015W/cm2,=0.0°,=2.0 a.u.。由图可知,除了平台区和截止能量等高次谐波所具有的普遍特征外,最重要的一个特点就是在低阶谐波处产生的谐波增强效应。具体来说,谐波谱总共出现了4个共振增强峰,分别出现在第36th、52nd、62nd、72nd阶谐波处。根据之前对HeH2+分子谐波发射的研究可知[7-8],这些共振增强峰是由基态与激发态之间的激光诱导电子跃迁造成的。
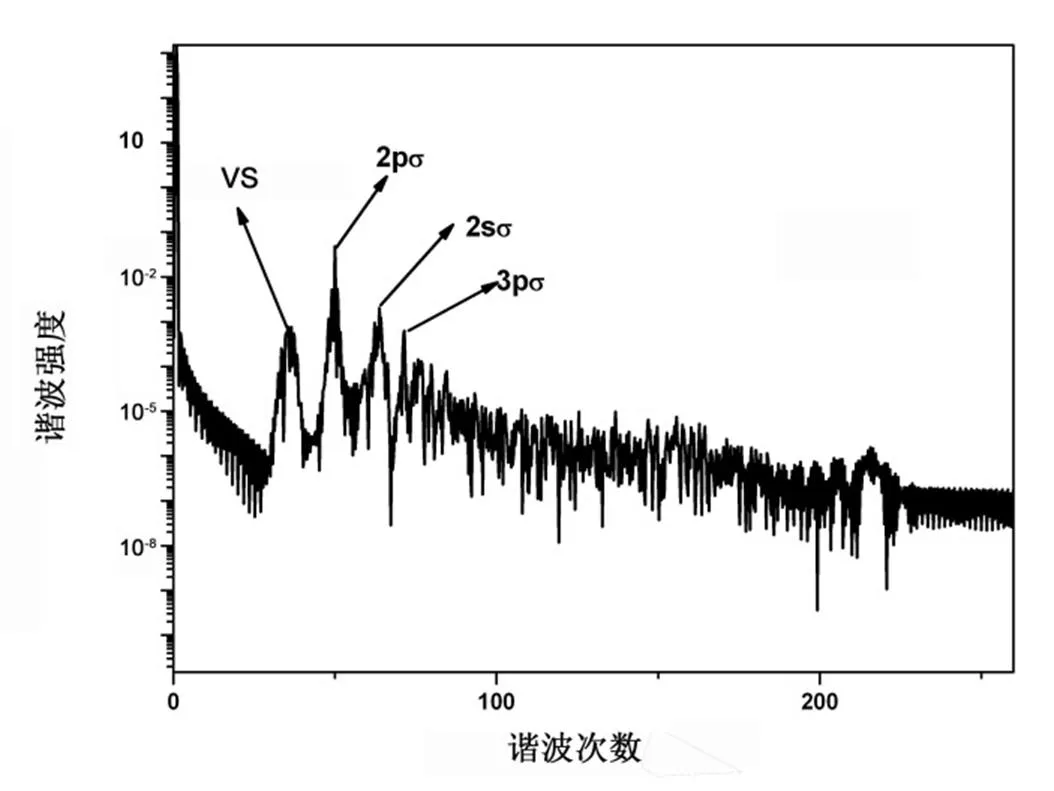
图1 LiH3+谐波发射功率谱图
图2给出了这一过程的简单示意图。首先,当激光场与LiH3+分子离子相互作用时,电子有一定的几率被激发到激发态。这一过程可以分为基态到激发态的直接激发(图中1、2通道),或者是从低激发态到高激发态之间的间接激发(图中3通道)。随后,激光场改变方向,处在激发态上的电子有一定的几率返回到基态并且发射出光子(图中4通道)。因此,在谐波谱上会出现较强的共振峰,其峰值的位置对应于基态(ES)与激发态(GS)之间的能量差(ES-GS)。
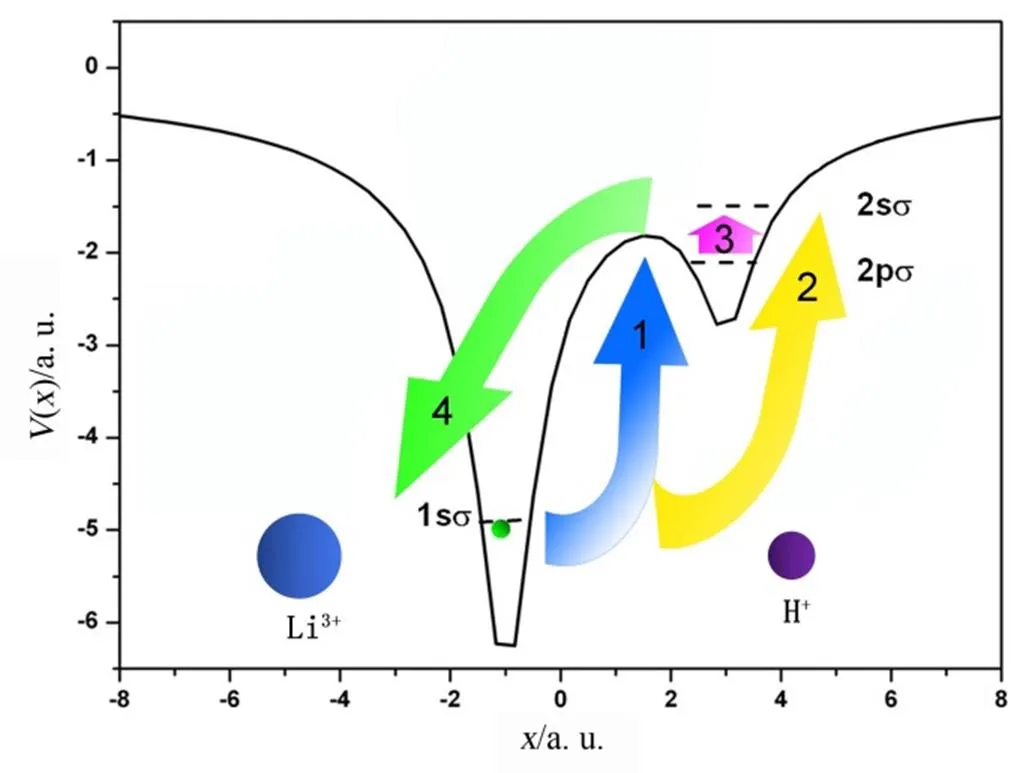
图2 基态与激发态之间激光诱导电子跃迁的示意图
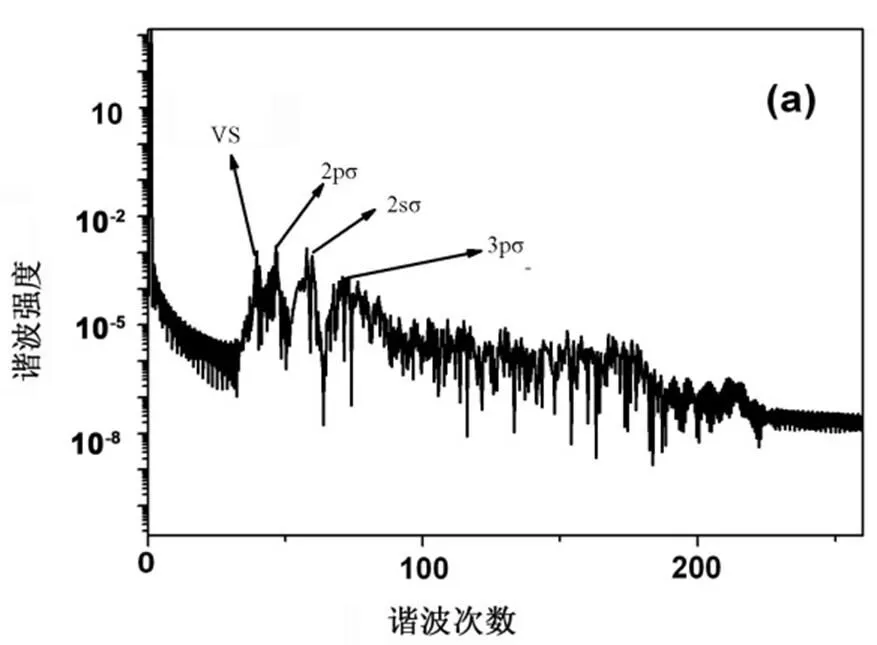
表1给出本文计算所得与实验情况下的LiH3+分子离子前几个电子态的能量。可以看出,本文的计算结果和实验值或者是三维的精确计算值[11-12]符合得较好。但是由于模型的缺陷本文计算值会多出一个不存在的虚态,记为VS。经过分析这些能量可知,前面出现的4个共振峰(36th、52nd、62nd、72nd)分别对应VS态、2pσ态、2sσ态、3pσ态与1sσ基态的能量差。
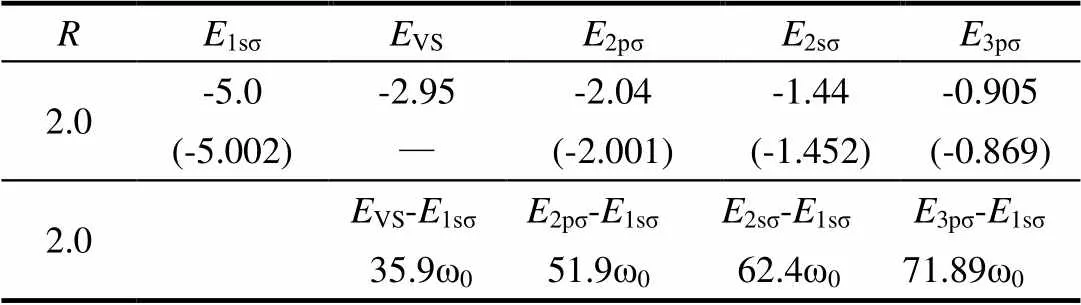
表1 LiH3+分子离子在R=2.0 a.u.时的电子态能量
注:括号中的能量来自文献[11-12]。
图3给出激光包络图以及电子在1sσ、2pσ、2sσ、3pσ态上的布局演化图。这里由于VS态是一个虚态所以不考虑其电子态上的布局。从图中可以看出,电子跃迁过程主要发生在激光场反向时,并且各激发态的跃迁强度不同,大致上满足2pσ>2sσ>3pσ,这和图1中各个共振峰的强度顺序相一致。
通过上面计算结果可知,激发态在不对称分子谐波发射中起到很重要的作用。但这些激发态效应是否普遍地存在于不对称分子中还不是很清楚。因此,为了理解这一问题,计算了LiH3+分子离子在不同参数下的高次谐波谱图。
(a)激光包络图
(b)电子在1sσ、2pσ、2sσ、3pσ态上的布局演化图
图3 激光场包络图及电子态布局
图4(a)和(b)分别给出了LiH3+分子离子在核间距=3.0 a.u.和=4.0 a.u.时的谐波谱图。激光参数与图1一样。可以看出,低阶谐波处的共振增强峰仍然存在。通过分析表2和表3中对应的电子态能量可知,这些共振峰分别对应于2pσ、2sσ、3pσ、3dσ激发态与1sσ基态之间的激光诱导跃迁过程。这里需要注意,对于其他的核间距,这些共振峰仍然是存在的,只是本文中并没有给出它们的谐波谱图。这说明,由激光诱导电子跃迁过程所形成的谐波共振峰是与分子核间距无关的。
(a)核间距=3.0 a.u.
(b)核间距=4.0 a.u.
图4 LiH3+分子离子谐波发射谱图
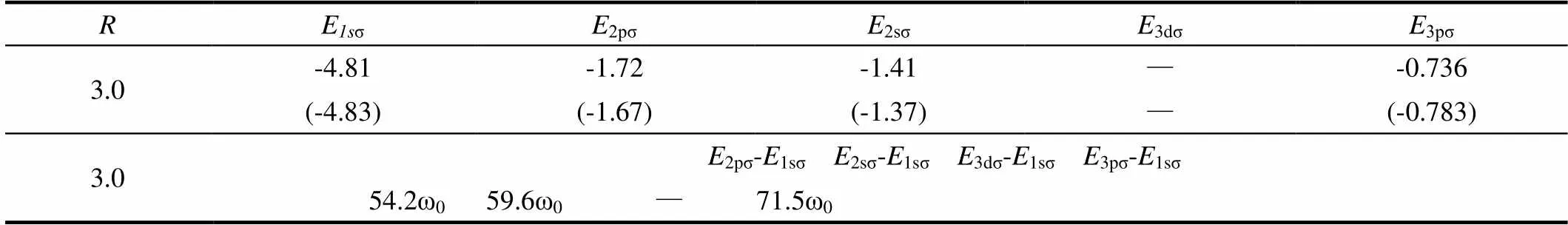
表2 LiH3+分子离子在R=3.0 a.u.时的电子态能量
注:括号中的能量来自文献[11-12]。

表3 LiH3+分子离子在R=4.0 a.u.时的电子态能量
注:括号中的能量来自文献[11-12]。
图5(a)~(d)分别给出了核间距=2.0 a.u.时LiH3+分子离子在不同波长(=400~700 nm),场强(=5.0×1014、1.5×1015、2.0×1015W/cm2),脉宽(=6、10 fs)和相位(=30°、60°、90°、150°)下发射谐波的特点。其他激光参数与图1中一样。很明显,无论怎样改变激光参数,依然可以观察到由2pσ、2sσ、3pσ激发态与1sσ基态之间的激光诱导电子跃迁所形成的3个共振峰,也就是说这一激光诱导电子跃迁过程是独立于激光参数的。
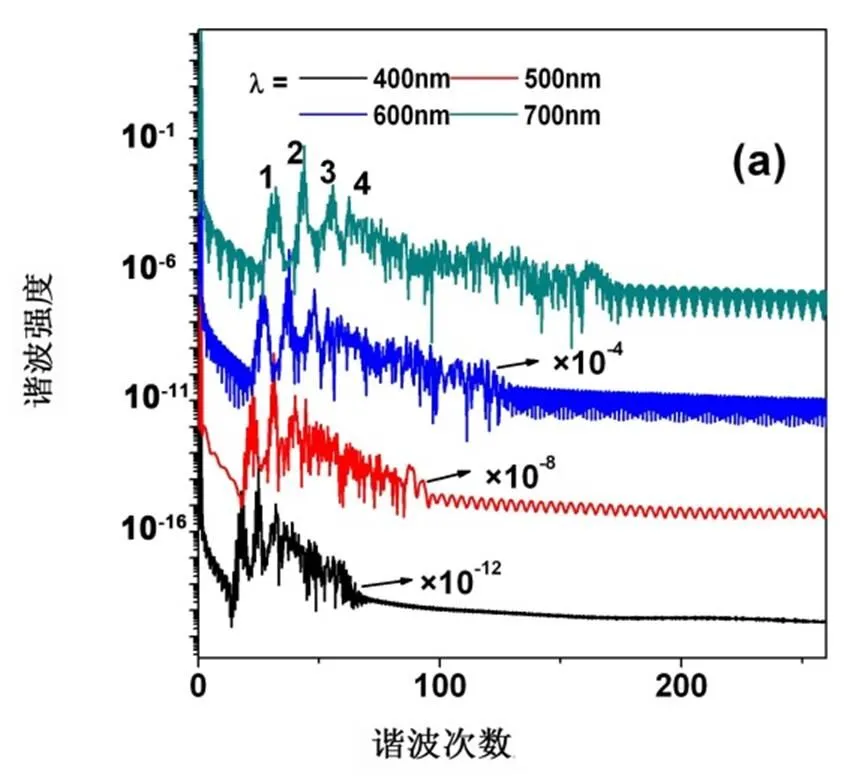
(a)波长(=400~700 nm)
(b)场强(=5.0×1014、1.5×1015、2.0×1015W/cm2)

(c)脉宽(=6、10 fs)
(d)相位(=30°、60°、90°、150°)
图5 LiH3+分子离子谐波发射谱图
3 结论
本文理论研究了激发态在不对称分子谐波发射过程中的作用。计算结果表明,在低阶谐波处会出现谐波共振增强的现象,这一现象是在原子或对称分子当中所观察不到的。通过分析各个电子态的能量以及布局随时间的演化,这些增强的谐波是由激发态与基态之间的激光诱导电子跃迁过程所产生的。并且通过计算不同参数下的高次谐波谱图可知,激发态效应或者说是谐波共振增强效应普遍存在于不对称分子电离过程中。
[1] Krausz F, Ivanov M. Attosecond physics[J]. Rev Mod Phys, 2009, 81(1): 163-234.
[2] Lewenstein M, Balcou P, Ivanov M Y, et al. Theory of high-harmonic generation by low-frequency laser fields[J]. Phys Rev A, 1994, 49(3): 2117-2132.
[3] Feng L Q, Chu T S. Generation of an isolated sub-40-as pulse using two-color laser pulses: Combined chirp effects[J]. Phys Rev A, 2011, 84(5): 053853.
[4] Corkum P B. Plasma perspective on strong field multiphoton ionization[J]. Phys Rev Lett, 1993, 71(13): 1994-1997.
[5] Lan P F, Lu P X, Cao W, et al. Carrier-envelope phase-stabilized attosecond pulses from asymmetric molecules[J]. Phys Rev A, 2007, 76(2): 021801.
[6] Chen Y J, Zhang B. Tracing the structure of asymmetric molecules from high-order harmonic generation[J]. Phys Rev A, 2011, 84(5): 053402.
[7] Bian X B, Bandrauk A D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules[J]. Phys Rev Lett, 2010, 105(9): 093903.
[8] Chen Y J, Zhang B. Role of excited states in the emission times of harmonics from asymmetric molecules[J]. Phys Rev A, 2012,86(2): 023415.
[9] Feng L Q.Molecular harmonic extension and enhancement from H2+ions in the presence of spatially inhomogeneous fields[J]. Phys Rev A, 2015, 92(5): 053832.
[10] Burnett K, Reed V C, Cooper J, et al. Calculation of the background emitted during high-harmonic generation[J]. Phys Rev A, 1992, 45(5): 3347-3349.
[11] CamposJ A, Nascimento D L, Cavalcante D T, et al. Determination of electronic energy levels for the heteromolecular ions HeH2+LiH3+, and BeH4+from the Hamilton-Jacobi equation[J]. Int J Quantum Chem, 2006, 106(13): 2587-2596.
[12] Arteca G A, Mezey P G. Simple analytic bounds for the electronic-energy from level set boundaries of nuclear-charge space[J]. Phys Rev A, 1987, 35(10): 4044-4050.
责任编校:孙 林
Effect of Excited State on Asymmetric Molecular Harmonic Emission
LIU Hang1, FENG Li-qiang2
(1.School of Chemical and Environmental Engineering, Liaoning University of Technology, Jinzhou 121000, China; 2.College of Science, Liaoning University of Technology, Jinzhou, 121001, China)
Effect of state excited on harmonic emission from the asymmetric molecule ion LiH3+has been theoretically investigated. Results show that the laser-induced electron transfer processes between the ground state and the first few excited states is responsible for the observed multiple frequencies enhancements on the low harmonics. Moreover, such electron transfer processes are very likely to be general characteristic for the asymmetric molecular ionization, as suggested by calculations for LiH3+at different internuclear distances and with different central frequencies, pulse intensities, carrier-envelope phases and pulse durations.
excited state;high-order harmonic generation (HHG); laser-induced electron transfer
10.15916/j.issn1674-3261.2017.02.001
O562.4
A
1674-3261(2017)02-0071-04
2016-05-13
国家自然科学基金项目(11504151);辽宁省博士启动基金项目(201501123);辽宁省教育厅基金项目(L2014242,JL201615405)
刘航(1985-),女,辽宁锦州人,讲师,博士。
