基于修正Johnson-Cook模型的钛合金热黏塑性动态本构关系及有限元模拟
2017-10-13李云飞曾祥国
李云飞,曾祥国,廖 异
基于修正Johnson-Cook模型的钛合金热黏塑性动态本构关系及有限元模拟
李云飞1, 2,曾祥国1,廖 异1
(1. 四川大学建筑与环境学院,成都610065;2. 中国工程物理研究院总体工程研究所,绵阳621999)
为了准确描述钛合金在高应变率、高温载荷下的热粘塑性本构行为,以及因材料内部出现绝热剪切带而导致材料流变应力减小的定量关系,构造功热转换系数与应变率之间的函数关系,提出一种基于修正Johnson-Cook模型的钛合金热粘塑性动态本构关系,并通过以最小二乘法为目标函数的局部搜索优化算法,对基于实验数据的本构参数进行快速优化识别。最后利用应力补偿更新算法,通过显式用户子程序VUMAT将热黏塑性本构模型嵌入ABAQUS软件中,得到Ti-6Al-4V钛合金在不同应变率、温度条件下的单轴动态应力−应变曲线。数值模拟结果与实验数据吻合良好,表明该修正模型能准确描述钛合金高应变率下的热黏塑性变形,可适用于各种应变率下钛合金本构行为的描述。
Ti-6Al-4V;热黏塑性;修正Johnson-Cook模型;用户子程序VUMAT
钛合金具备密度小、比强度高及耐腐蚀与耐热性能优异等特点,被广泛应用于航空航天、船舶、化工及兵器工业等领域[1]。随着科学技术的迅猛发展,这些工业化领域对材料的要求越来越高,先进钛合金也逐步向具有高断裂韧性和低裂纹扩展速率的损伤容限型钛合金方向发展。在材料性能方面,诸多研究发现钛合金在高应变率和准静态载荷下的力学性能存在显著差异[2−6]。
目前,常用的金属材料动态本构模型主要为两 类[7−9],一类是唯象经验型本构模型,如Johnson-Cook模型等;另一类是从材料的微观变形机制出发,称为物理本构模型。Johnson-Cook模型因形式简单、各参数含义明确、参数较少且容易通过试验拟合等优点已被LS/DYNA、MSC/DYTRAN、ABAQUS/EXPLICIT等软件用于动力学有限元分析。但KHAN等[10]研究发现,Johnson-Cook 模型对钛合金动态拉伸行为的拟合能力较差。在高应变率下钛合金表现出热黏塑性,其内部绝热温升成为影响其本构关系的重要因素,而温度的升高降低了应变、应变率的强化作用,反过来,强化作用的减弱又减缓了温度的上升。Johnson-Cook模型无法描述温度、应变、应变率三者互相作用、互相影响的复杂现象。
张长清等[11]通过Hopkinson压杆试验拟合得到TC4钛合金在不同应变率与绝热温升的关系曲线,并对Johnson-Cook模型温度项进行改进得到室温下材料的动态塑性本构方程,但该本构无法描述高应变率下的热黏塑性行为。杨扬等[12]引入材料应力−应变曲线发展趋势项提出一种拟合Johnson-Cook方程的简便方法,避免了对相对不稳定的材料绝热温升值的估算。俞秋景等[13]将应变速率硬化系数修改为随温度和应变速率变化的量对Johnson-Cook方程进行改进,考虑了Inconel625合金考虑了温度、应变和应变速率对流变应力的交互影响。成生伟等[14]令温度软化系数=1求解出绝热温升项的简单解,进而修正Johnson-Cook模型得到电铸Ni-W合金高应变率下的动态响应。上述修正Johnson-Cook模型无法较好地描述钛合金热黏塑性的流变应力特征,并且部分本构方程改进后形式较复杂,无法通过用户子程序接口导入有限元软件中。
本文作者基于Ti-6Al-4V钛合金在不同应变率、温度下的流变应力−塑性应变实验数据,构造了功热转换系数与应变率之间的函数关系[15],提出一种基于修正Johnson-Cook模型的钛合金热黏塑性动态本构关系,并通过以最小二乘法为目标函数的局部搜索优化算法,对基于实验数据的本构参数进行快速优化识别,构建出可准确描述热黏塑性行为的动态本构方程。利用应力补偿更新算法,通过显式用户子程序VUMAT将热黏塑性本构模型嵌入ABAQUS中,得到不同应变率、温度条件下的数值模拟结果,与实验数据对比可验证修正本构模型的适用性以及子程序的准确性。
1 修正本构模型
Johnson-Cook模型能够反映应变硬化、应变率硬化和温度软化效应,其流变应力−塑性应变表达式为
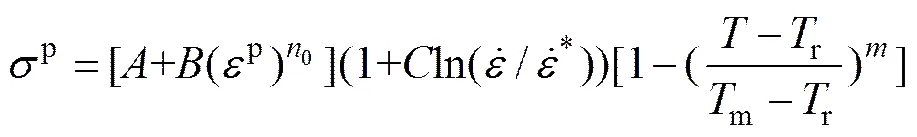
式中:、、0、、为本构参数;为流变应力;为塑性应变;为实际应变率;为参考应变率,通常取为1 s−1;为试验温度;r为参考温度,通常取为室温;m为材料的熔点温度。
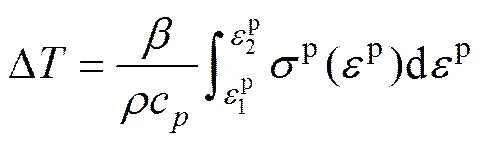
(3)
式中:为功热转换系数(绝热状态下=1);为材料密度;c为定压比热容。
根据功热转换原理,外力对材料拉伸所做的功会转换为热能,其一部分会耗散到自然界中,另一部分会使材料自身温度升高。但在低应变率下,由于材料拉伸速度缓慢,材料温度与外界温度能充分进行热传递,故外力对材料所做的功并不会使材料内部温度明显升高,即:当时,;而在高应变率下,材料被快速拉伸,由外力功转换的热能来不及与外界温度充分进行热传递,故材料内部温度会明显升高,即随的增大而增大,当时,(当=1则为绝热状态)。因此,构造满足上述与关系的函数表达式为
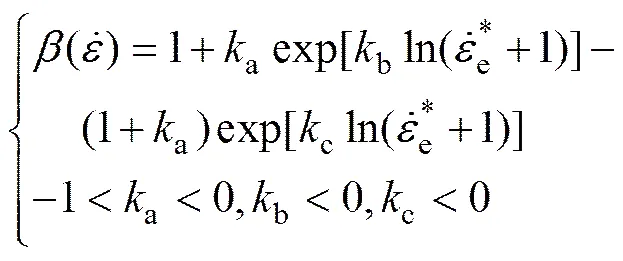
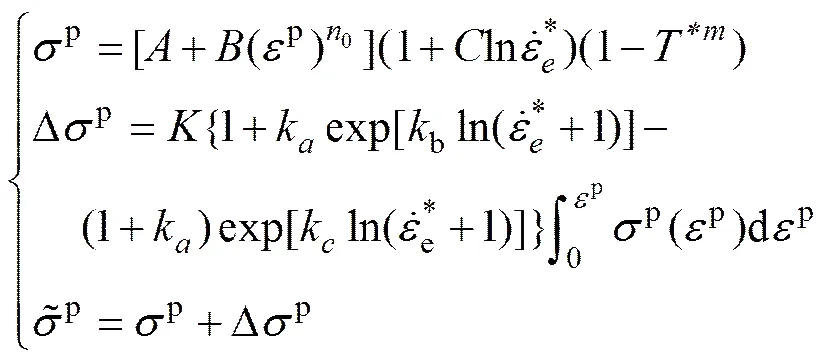
2 本构参数优化识别
根据实验数据,按以下步骤确定修正Johnson-Cook模型的各待定本构参数:
1) 不考虑应变率硬化和温度软化时,经典Johnson-Cook模型可简化为
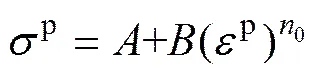
(7)
在对数坐标系下,式(7)为线性方程,可用最小二乘法对实验曲线作线性拟合,求得、0,记,。
2) 仅考虑应变硬化和应变率硬化时,经典Johnson-Cook模型可简化为
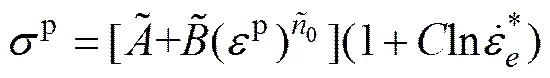
式(8)中仅含待定本构参数。可对不同应变率下获得的实验数据分别拟合,再通过取平均值的方法最终确定出。
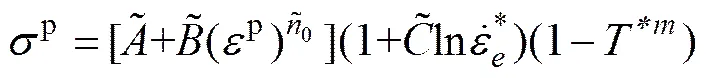
式(9)中仅含待定本构参数。可对非常温下的各组实验数据分别拟合,再通过取平均值的方法最终确定出。
4) 此时,经典Johnson-Cook模型的5个本构参数已全部确定,方程为
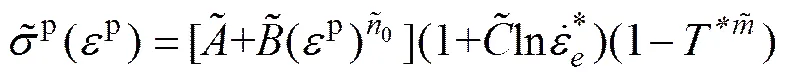
(11)
式中:()为目标函数;为离散设计变量;为各离散设计变量的局域搜索范围,一般取10%~50%;ΔX为各离散设计变量的搜索间隔,一般取=1%×。优化完毕后,用最优离散设计变量opt更新经典JC模型的5个本构参数、、、、。
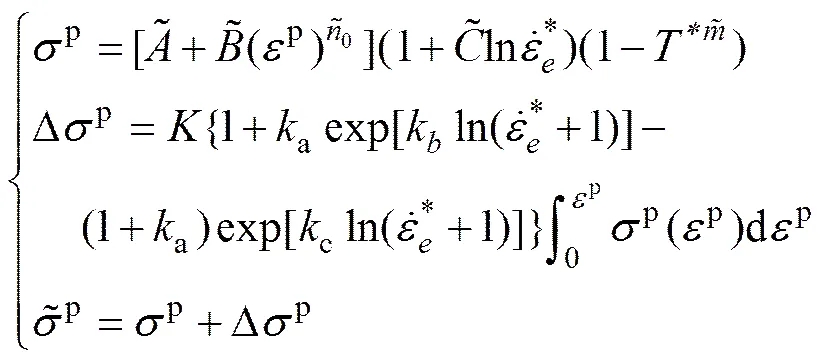
此时,式(12)中含有的待定本构参数有a、b、c、。以>1×102s−1的所有实验数据点(=1,2,…,)为参照,以最小二乘法为目标函数,可同样采用式(11)所示的搜索方法确定出本构参数,,,。至此,修正Johnson-Cook模型中的9个本构参数已全部确定。
采用文献[10]中的实验数据,通过式(11)所示搜索优化方法,得到Ti-6Al-4V钛合金修正Johnson-Cook模型中的9个本构参数优化结果如表1所示。

表1 修正Johnson-Cook模型中Ti-6Al-4V钛合金的本构参数
相比Johnson-Cook模型,修正模型的形式不便于通过VUMAT用户子程序进行编程,因此,将式(12)中的第一式代入第二式中进行求解,同时代入各本构参数的优化值,则Ti-6Al-4V钛合金的动态本构方程为
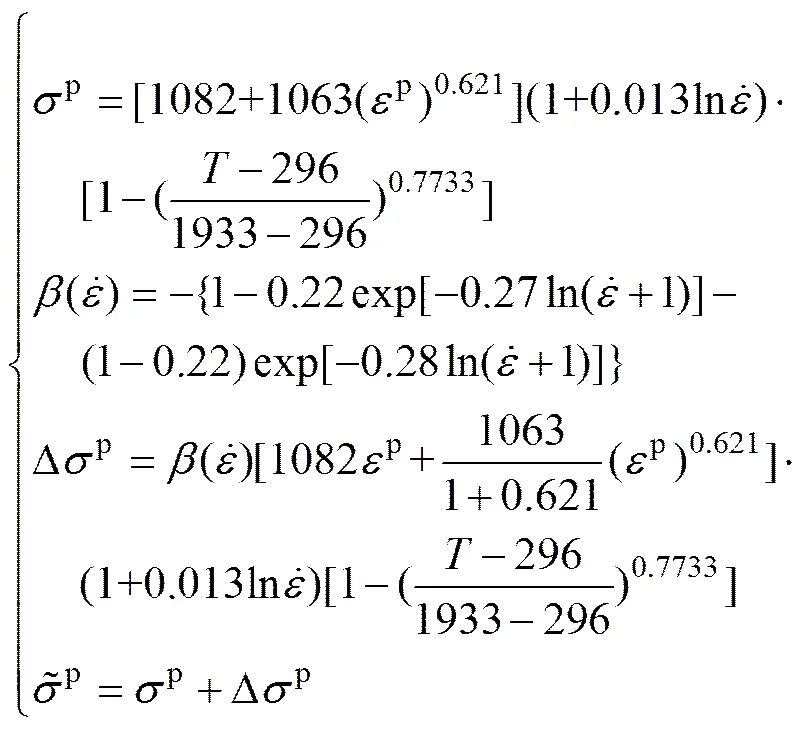
3 有限元模拟方法
3.1 VUMAT与应力补偿更新算法
为了将本实验中Ti-6Al-4V钛合金修正Johnson-Cook动态本构模型应用于有限元计算,本文作者基于ABAQUS有限元软件进行了二次开发。ABAQUS提供了FORTRAN语言编写的专门用于定义材料模型的用户子程序接口,分别是UMAT和VUMAT。二者的数据结构是相似的,主要不同之处在于UMAT中需要形成Jacobian矩阵,即应力增量对应变增量的变化率,而在VUMAT中则不需要求Jacobian矩阵,此外在子程序与主程序的接口处二者也有细微差别。
本研究中采用显式用户材料子程序VUMAT接口对修正Johnson-Cook模型进行定义,适用于冲击、高速率应变等瞬时载荷下的结构响应有限元模拟,可有效减少计算时间,提高计算效率。应力张量更新算法的选择是VUMAT子程序编写过程中的核心问题。传统黏塑性应力更新算法中若材料点已进入塑性变形阶段,则应变增量由弹性部分和黏塑性部分组成(),弹性部分应力增量由广义Hooke定律得,黏塑性部分应力增量为
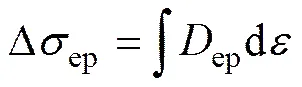
式中:ep为黏塑性张量,且ep=e−p,e为弹性张量,p为塑性张量。塑性变形阶段的应力增量为Δe与Δep之和。该算法中每一增量步必须首先对ep进行迭代更新,计算量大效率低,且易累计误差,影响计算结果精度。
本实验中采用基于弹性张量的应力补偿更新算法[16−17],算法原理如图1所示。首先判断当前状态下材料点是否屈服,若屈服则应变增量。假定应变张量全为弹性的,由广义Hooke定律计算试探应力增量以及试探应力,然后在试探应力的基础上减去多算的塑性应变增量对应的应力增量部分,对试探应力进行负补偿。即
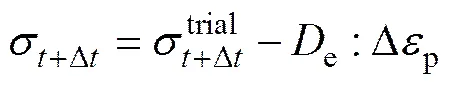
由式(15)可知,该算法没有迭代积分,计算中只需要恒定的弹性张量e,可以显著减小计算量,提高计算效率。
3.2 修正模型的VUMAT开发
ABAQUS用户子程序VUAMT的接口提供了依赖于结果的状态变量,用于存储在计算时用户定义的需要不断更新的状态变量。实现Ti-6Al-4V钛合金修正Johnson-Cook模型的子程序计算步骤如下,其计算流程如图2所示。具体如下:1) 从ABAQUS子程序接口读入本增量步的应变增量Δ,增量步开始时的应力张量t和等效塑性应变;2) 计算试探应力;3) 调用子程序,计算初始流变应力f;4) 将试探应力代入屈服准则,判断是否屈服;5) 若没有屈服,则转到(8);6) 如果发生屈服,计算本增量步的塑性应变增量,采用径向返回应力补偿算法更新本增量步结束时的应力; 7) 更新内能,塑性功,等效塑性应变及各状态变量的值;8) 结束,返回主程序。
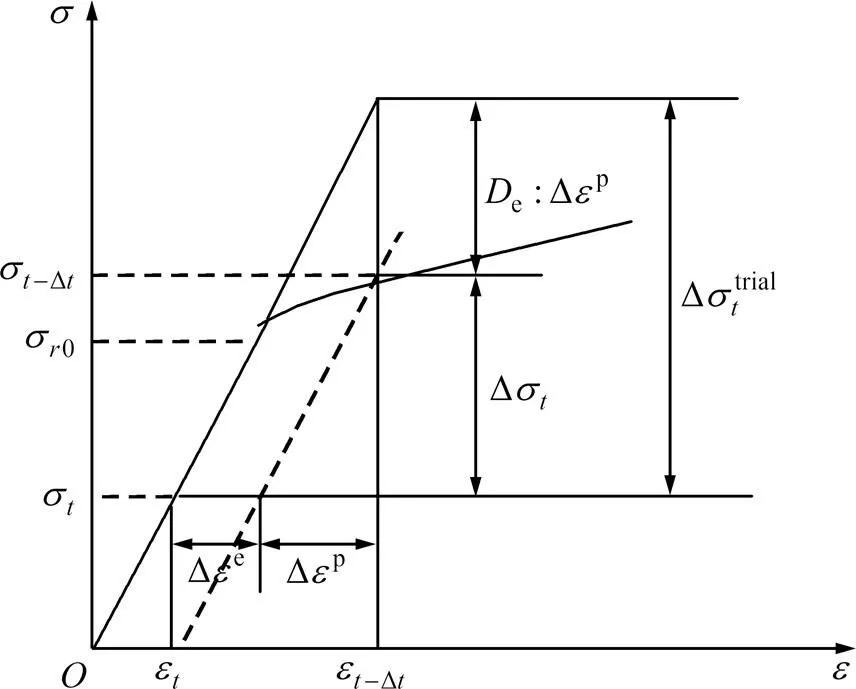
图1 应力补偿更新算法示意图
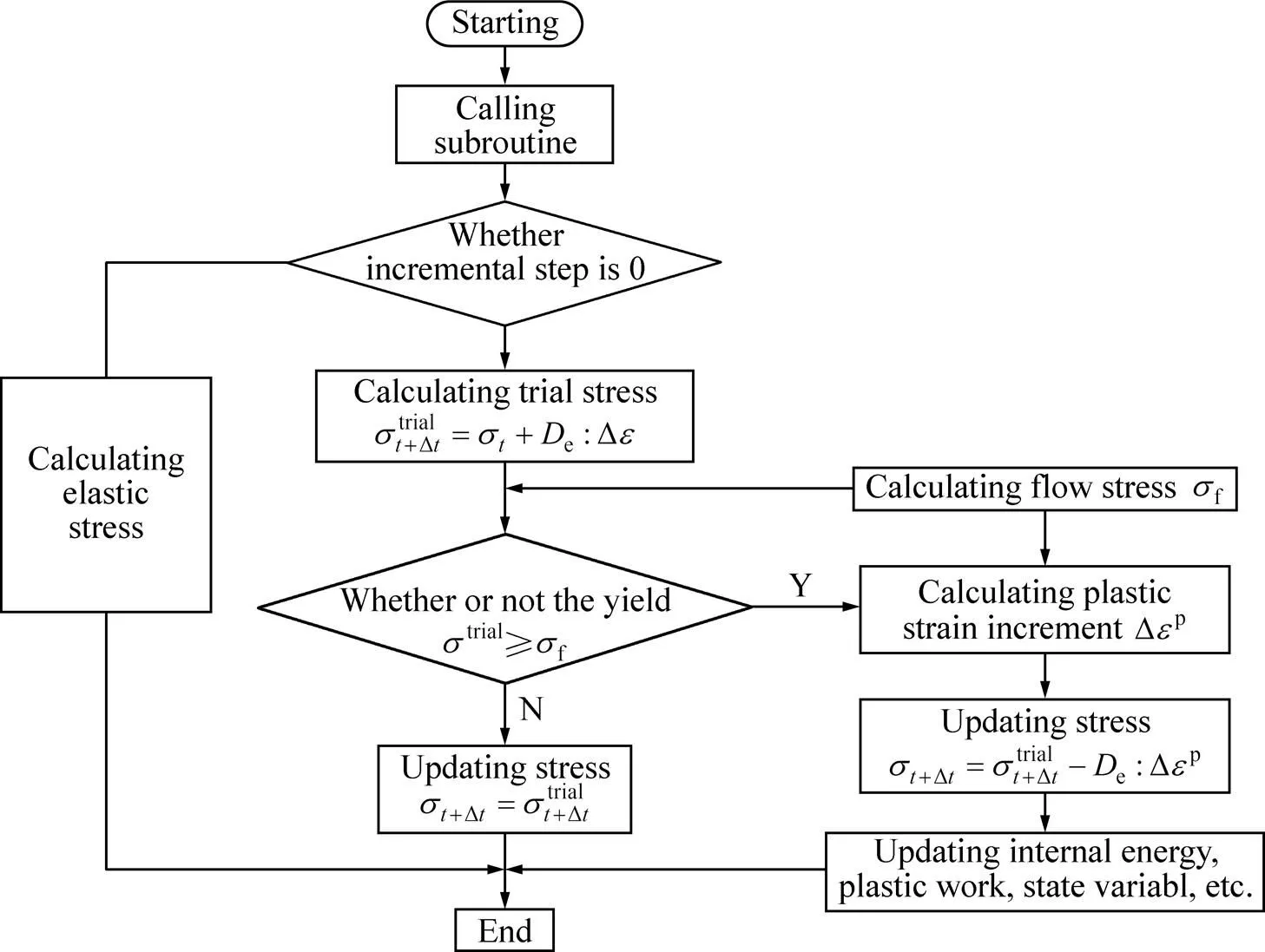
图2 VUMAT子程序计算流程图
4 模拟结果与讨论
基于应力补偿更新方法,按照ABAQUS用户子程序接口规范,通过FORTRAN语言编写Ti-6Al-4V修正Johnson-Cook模型的VUMAT用户子程序,本构参数采用表1中的优化识别结果。考虑到材料行为与结构形态无关,本文作者采用单个八节点六面体等参元(C3D8R)计算Ti-6Al-4V钛合金在单轴加载条件下的动态响应。
为验证修正Johnson-Cook模型对热黏塑性变形的适用性,通过ABAQUS有限元软件首先模拟了Ti-6Al-4V钛合金在常温(=296 K)下,低应变率与中、高应变率时的应力应变曲线,并与经典Johnson-Cook模型的预测结果对比如图3(a)和(b)所示。由图3可知,修正模型在低率时与经典模型预测结果保持一致,在中、高应变率时二者结果随应变而逐渐偏离,修正模型出现流变应力下降现象。
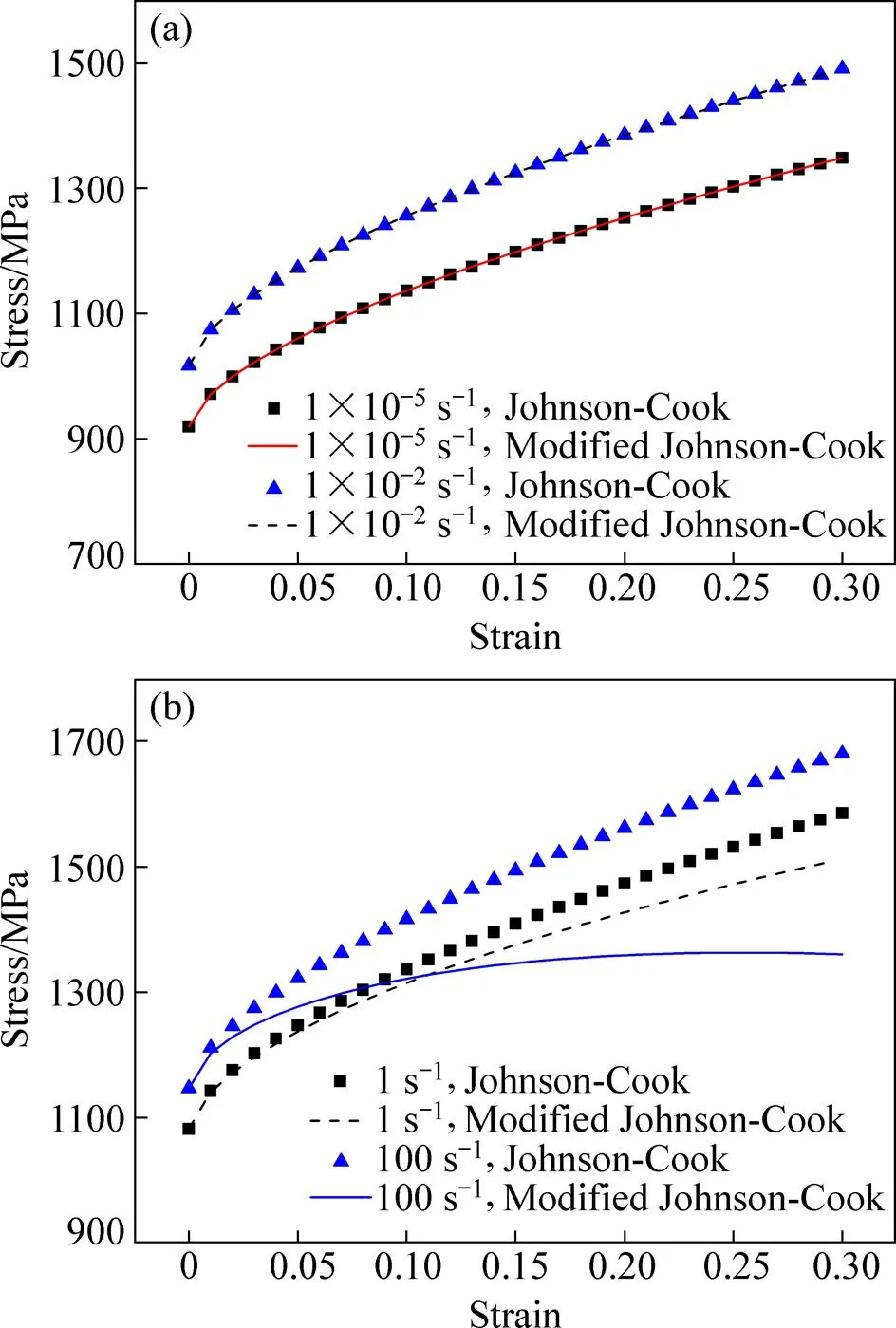
图3 不同应变率下修正Johnson-Cook模型结果与经典模型预测结果对比
修正Johnson-Cook模型在中应变率及以下不同载荷情况的模拟结果与文献[10]实验数据的比较如图4和5所示。图4所示为常温(=296 K)下分别为1×10−5、1×10−3、1×1 s−1时,Ti-6Al-4V钛合金应力−应变曲线的实验和模拟数据对比。图5所示为准静态(=1×10−3s−1)下温度分别为755、588、422 K时,Ti-6Al-4V钛合金应力−应变曲线的实验和模拟数据对比。由图4和5可知,修正的Johnson-Cook模型在中应变率及以下(<1×101s−1)加载条件的有限元模拟结果与实验数据吻合良好,该模型可准确描述Ti-6Al-4V钛合金的本构关系。
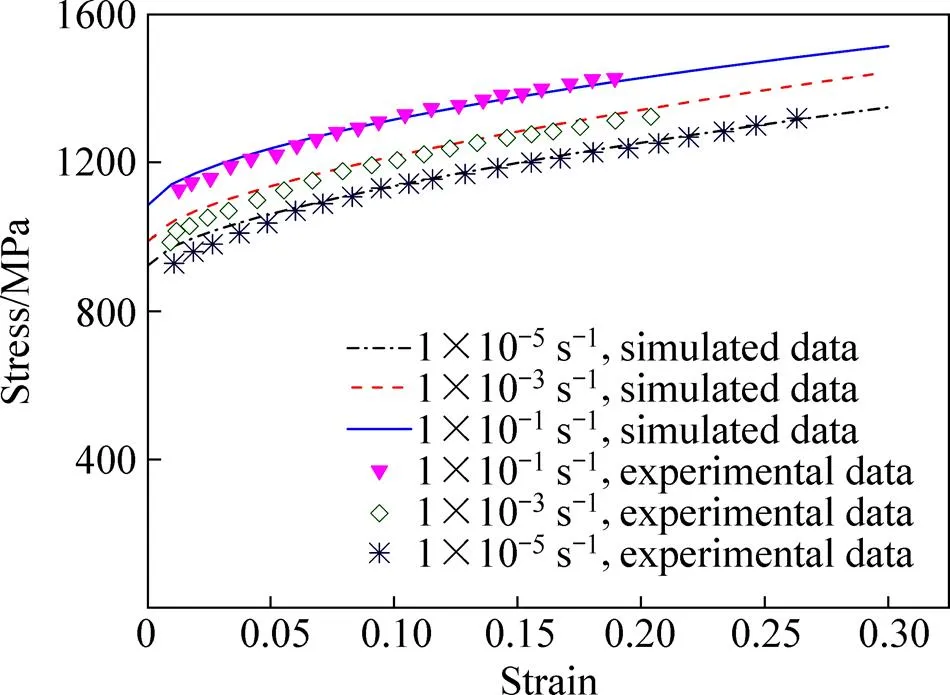
图4 常温下不同应变率时的实验与模拟数据对比
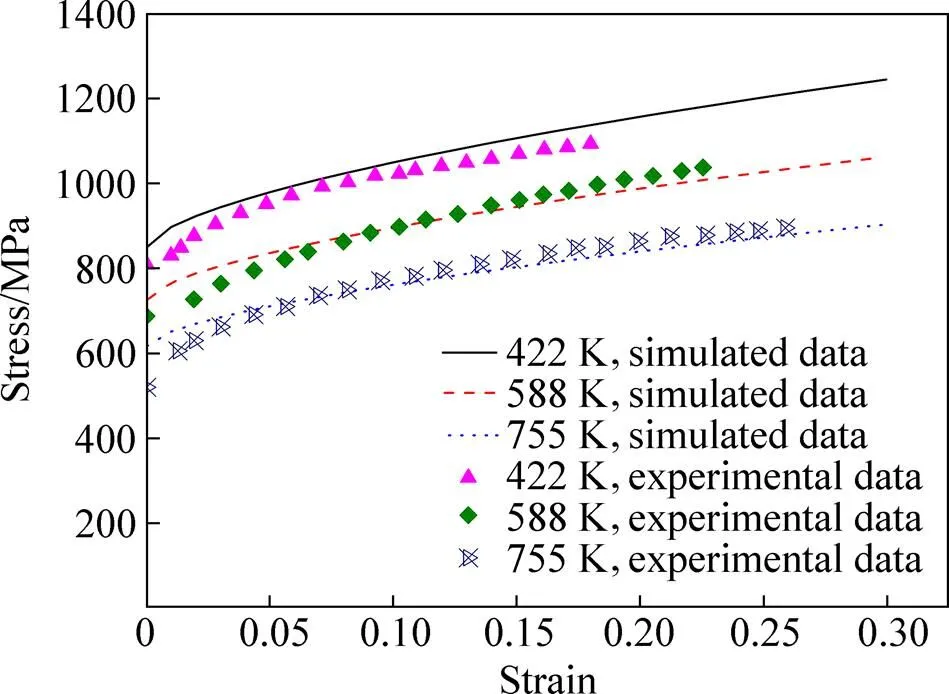
图5 准静态下不同温度时的实验与模拟数据对比
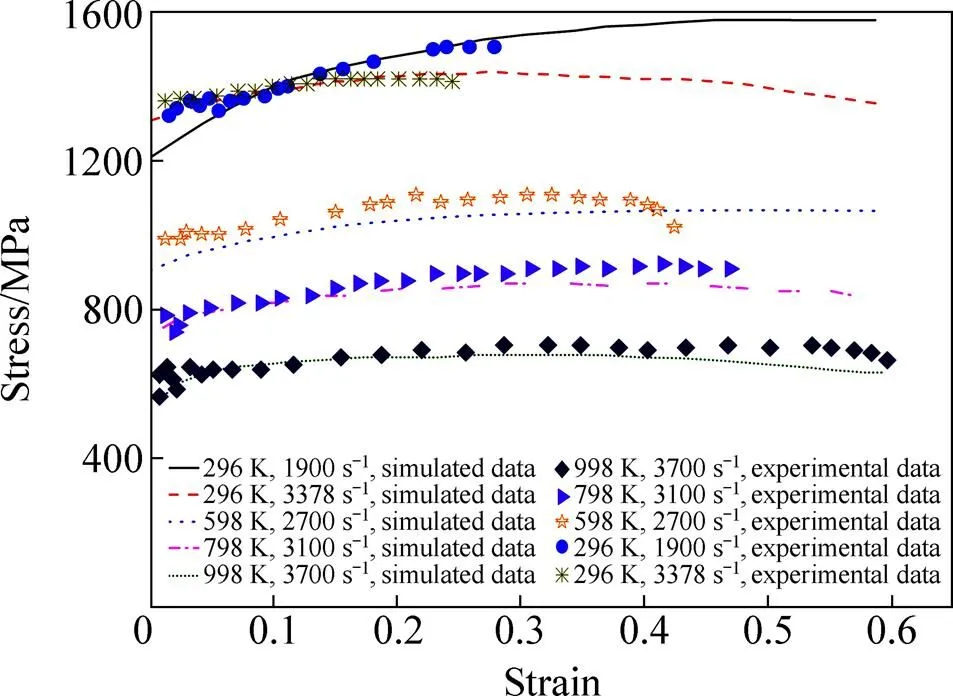
图6 不同温度高应变率下Ti-6Al-4V的实验与模拟数据对比
5 结论
1) 通过构造功热转换系数与应变率的函数关系,建立的修正Johnson-Cook模型适用于不同应变率下的Ti-6Al-4V钛合金本构行为描述,特别是高应变率下出现的热黏塑性变形行为。
2) 采用最小二乘法为目标函数的局部搜索优化算法,对基于实验数据的本构参数进行快速优化识别,并利用应力补偿更新算法,通过显式用户子程序VUMAT将热黏塑性本构模型嵌入ABAQUS中,得到Ti-6Al-4V钛合金在不同应变率、温度条件下的数值模拟结果与实验数据吻合良好,验证子程序的准确性与适用性。
3) 在高应变率下,Ti-6Al-4V钛合金表现出热黏塑性,材料内部绝热温升成为影响其本构关系的重要因素。根据本研究的模拟结果,在相同的外部温度下,随着塑性应变的增大,Ti-6Al-4V钛合金在高应变率下流变应力的变化梯度比低应变率下流变应力的变化梯度更平缓,建立的修正Johnson-Cook模型能够较准确描述钛合金在高应变率下的热黏塑性行为。
REFERENCES
[1] 曹春晓. 选材判据的变化与高损伤容限钛合金的发展[J]. 金属学报, 2002, 38(增刊): 4−11. CAO Chun-xiao. Change of material selection criterion and development of high damage-tolerant titanium alloy[J]. Acta Metallurgica Sinica, 2002, 38(Supple): 4−11.
[2] 徐天平, 王礼立, 卢维娴. 高应变率下钛合金Ti-6Al-4V的热-粘塑性特性和绝热剪切变形[J]. 爆炸与冲击, 1987, 7(1): 1−8.XU Tian-ping, WANG Li-li, LU Wei-xian. The thermo-viscoplasticity and adiabatic shear deformation for a titanium alloy Ti-6Al-4V under high strain rates[J]. Explosion and Shock Waves, 1987, 7(1): 1−8.
[3] 宫旭辉. 高温环境下+钛合金的动态拉伸力学行为—测试、分析与表征[D].合肥: 中国科学技术大学, 2010. GONG Xu-hui. Dynamic tensile behavior of+titanium alloy at elevated temperatures−Test, analysis and description[D]. Hefei: University of Science and Technology of China, 2010.
[4] Majorell A, STRIVATSA S, PICU R C. Mechanical behavior of Ti-6Al-4V at high and moderate temperatures−PartⅠ: Experimental results[J]. Materials Science and Engineering A, 2002, 326(2): 297−305.
[5] LEE W S, Lin C F. Plastic deformation and fracture behavior of Ti-6Al-4V alloy loaded with high strain rate under various temperatures [J]. Materials Science and Engineering A, 1998, 241(1): 48−59.
[6] Chiou S T, Tsai H L, Lee W S. Impact mechanical response and micro structural evolution of Ti Alloy under various temperatures[J]. Journal of Materials Processing Technology, 2009, 209(5): 2282−2294.
[7] GAO C Y, Zhang L C. Constitutive modeling of plasticity of fcc metals under extremely high strain rates[J]. International Journal of Plasticity, 2012, 32(5): 121−133.
[8] KHAN A S, LIU H. Variable strain rate sensitivity in an aluminum alloy: Response and constitutive modeling[J]. International Journal of Plasticity, 2012, 36(9): 1−14.
[9] 周 霞, 赵昌美, 李 利, 黄宏军. 基于SPHB实验的挤压AZ91D镁合金动态力学行为数值模拟[J]. 中国有色金属学报, 2014, 24(8): 1968−1975. ZHOU Xia, ZHAO Chang-mei, LI Li, HUANG Hong-jun. Numerical simulation of dynamic behavior of extruded AZ91D magnesium alloy based on SPHB experiment[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(8): 1968−1975.
[10] KHAN A S, SUH Y S, KAZMI R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12): 2233−2248.
[11] 张长清, 谢兰生, 陈明和, 商国强. 高应变率下TC4-DT 钛合金的动态力学性能及塑性本构关系[J].中国有色金属学报, 2015, 25(2): 323−329. ZHANG Chang-qing, XIE Lan-sheng, CHEN Ming-he, SHANG Guo-qiang. Dynamic mechanical property and plastic constitutive relation of TC4-DT Ti alloy under high strain rate[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 323−329.
[12] 杨 扬, 曾 毅, 汪冰峰. 基于Johnson-Cook模型的TC16钛合金动态本构关系[J].中国有色金属学报, 2008, 18(3): 505−510. YANG Yang, ZENG Yi, WANG Bing-feng. Dynamic constitutive relationship of TC16 titanium alloy based on Johnson-Cook model[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(3): 505−510.
[13] 俞秋景, 刘军和, 张伟红, 于连旭, 刘 芳, 孙文儒, 胡壮麒. Inconel 625合金Johnson-Cook本构模型的一种改进[J].稀有金属材料与工程, 2013, 42(8): 1679−1684.YU Qiu-jing, LIU Jun-he, ZHANG Wei-hong, YU Lian-xu, LIU Fang, SUN Wen-ru, HU Zhuang-qi. Modification of Johnson-Cook model for hot deformation behavior of Inconel 625 alloy[J]. Rare Metal Materials and Engineering, 2013, 42(8): 1679−1684.
[14] 成生伟, 田文怀. 电铸Ni-W合金高应变率下流变应力特征[J]. 兵器材料科学与工程, 2012, 35(3): 34−38. CHENG Sheng-wei, TIAN Wen-huai. Flow stress characteristics of electroformed Ni-W alloy at high strain rates[J]. Ordnance Material Science and Engineering, 2012, 35(3): 34−38.
[15] 曾祥国, 盛 鹰, 韩悌信, 陈 军, 陈华燕. 考虑热粘塑性钛合金动态本构关系及其实验验证[J]. 四川大学学报(工程科学版), 2014, 46(6): 152−157. ZENG Xiang-guo, SHENG Ying, HAN Ti-xin, CHEN Jun, CHEN Hua-yan. Dynamic constitutive relation considering thermo viscoplasticity for titanium alloy and experimental verification[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(6): 152−157.
[16] GAO C Y. FE realization of thermo-visco-plastic constitutive models using vumat in abaqus/explicit program[C]//Proceedings of Computational Mechanics. Beijing: Tsinghua University Press & Springer, Compatation and Mechanics, 2007: 623−628.
[17] 孙河洋, 马吉胜, 生龙波, 刘海平, 吴大林. 某型铜材料动态力学性能的数值模拟研究[J]. 军械工程学院学报, 2011, 23(5): 75−78. SUN He-yang, MA Ji-sheng, SHENG Long-bo, LIU Hai-ping, WU Da-lin. Study on the numerical simulation of a Cu material’s dynamic mechanical property[J]. Journal of Ordnance Engineering College, 2011, 23(5): 75−78.
(编辑 龙怀中)
Thermal-viscoplastic constitutive relation of Ti-6Al-4V alloy and numerical simulation by modified Johnson-Cook modal
LI Yun-fei1, 2, ZENG Xiang-guo1, LIAO Yi1
(1.College of Architecture and Environment, Sichuan University, Chengdu 610065, China;2. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China)
In order to accurately describe the thermo viscoplasticity constitutive behavior of titanium alloy under high strain rate and elevated temperature, a modified Johnson-Cook equation was proposed by constructing function of conversion coefficient about strain rate. And the quantitative relation between decreasing flow stress and adiabatic shear band appeared in the material was analyzed. All the constitutive parameters could be quickly identified by the local search optimization algorithm taking least squares method as the object function. By adopting a stress compensation updating algorithm, a subroutine VUAMT of the proposed constitutive model was programmed on plat of ABAQUS/Explicit. The finite element simulation of dynamic responses of Ti-6Al-4V titanium alloy under different strain rates and temperatures are obtained. The modified Johnson-Cook modal can accurately describe the thermo viscoplasticity dissipation due to good agreement between simulation results and experimental data. The subroutine VUAMT and applicability of constitutive description for titanium alloy under various strain rates were verified.
Ti-6Al-4V; thermo viscoplasticity; modified Johnson-Cook modal; subroutine VUAMT
Project (B1520132013-1) supported by the National Natural Science Foundation of China Academy of Engineering Physics and Jointly Set Up “NSAF” Joint Fund
2016-06-28; Accepted date: 2016-10-25
LI Yun-fei; Tel: +86-816-2482384; E-mail: yunfei_ise@163.com
10.19476/j.ysxb.1004.0609.2017.07.13
1004-0609(2017)-07-1419-07
TG113.25
A
国家自然科学基金委与中国工程物理研究院NSAF联合基金资助项目(B1520132013-1)
2016-06-28;
2016-10-25
李云飞,助理研究员;电话:0816-2482384;E-mail:yunfei_ise@163.com
