TC11钛合金应变率相关力学行为的实验和本构模型

张 军，汪 洋，王 宇



TC11钛合金应变率相关力学行为的实验和本构模型

张 军1，汪 洋2，王 宇2

(1. 中国工程物理研究院总体工程研究所，绵阳621999；2. 中国科学院材料力学行为和设计重点实验室中国科学技术大学近代力学系，合肥230027)

利用MTS、中应变材料试验机和分离式霍普金森拉杆获得TC11钛合金在应变率1×10−3~1×103s−1范围内的应力−应变曲线，利用金相显微镜和扫描电子显微镜观察材料组织和断口形貌，基于修正的Johnson-Cook本构模型进行不同应变率下拉伸力学行为的有限元数值模拟。结果表明：TC11的初始屈服行为表现出明显的应变率强化特性，在中应变率范围内呈现出应变率不太敏感向应变率敏感的转折现象，材料的应变硬化率随着应变率的提高而逐渐降低。TC11的晶和片层+束被拉长，呈现韧性断裂机制。修正Johnson-Cook模型计及应变率对初始屈服应力和应变硬化行为的不同影响，数值计算曲线与试验曲线吻合较好，能够较好地应用于TC11应变率相关力学行为的数值仿真。

钛合金；应变率；本构模型

+型钛合金以其高比强度、耐腐蚀、无磁性、高损伤容限等优点，是军事和民用领域内的重要轻质结构材料[1−2]。由于其加工和服役中不可避免地经历高速切割、锻造成型、外物碰撞等高应变率条件，因此+型钛合金应变率相关的力学行为研究一直受到材料学家和力学科技工作者的广泛关注。

国内外大量的研究结果表明+型钛合金是应变率敏感材料。KHAN等[3]分析了Ti-6Al-4V在应变率 1×10−6~3378 s−1时环境温度在233~755 K范围内的压缩应力−应变行为，并给出了温度和应变率相关的KHL本构模型。NEMAT-NASSER等[4]较为系统地研究了Ti-6Al-4V在应变率1×10−3~7000 s−1、环境温度从77~1000 K范围内的本构行为，以及高应变率压缩下绝热剪切带内的显微组织演化规律。周舸等[5]和宫旭辉[6]分别研究了TC21钛合金的热压缩变形行为和动态拉伸力学行为。张长清等[7]、杨扬等[8]则分别给出了TC4-DT合金和TC16合金的Johnson-CooK模型。

Ti-6.5Al-3.5Mo-1.5Zr-0.3Si合金(简称TC11)属于Ti-Al-Mo-Zr-Si系+型钛合金，主要用于制造发动机压气机盘、叶片和鼓筒等关键零部件以及飞机结构件。目前，对TC11力学行为的研究主要集中在低应变率的热变形和组织演化规律等方面[9−13]，对其在中应变率(1×100~1×101s−1)以及高应变率(1×102~1×103s−1)范围内的拉伸力学行为研究报道较少。本文作者拟对国产+型钛合金TC11在应变率1×10−3~1×103s−1范围内的拉伸力学行为进行实验研究，揭示其应变率相关性；在此基础上，建立率相关的本构模型，供钛合金工程数值计算参考使用。

1 实验

1.1 试验材料

试验用钛合金为中国宝钛集团所提供的TC11棒材，其化学成分为(质量分数，%)6.6Al，3.3Mo，1.8Zr，0.29Si，0.07Fe，0.01C，0.01N，0.004H，0.13O以及Ti。试验前，进行双重热处理(先实施955℃,2 h固溶+空冷，再进行530℃,6 h时效+空冷)，一方面消除组织非均匀性，另一方面获得综合性能更加优异的双态组织。

1.2 试验方案

应变率1×102~1×103s−1内的动态拉伸测试在分离式霍普金森拉杆装置(SHTB)上进行，中应变率1×100~1×102s−1和准静态的拉伸测试则分别在中应变率材料试验机和MTS809上进行。

高应变率拉伸试验原理和装置示意图详见参考文献[14−15]。与其他霍普金森拉杆测试装置相比，该装置的特色之处在于拉伸方波脉冲的产生，基于机械滤波的思想，利用高速旋转盘，实施双片锤头与撞块的撞击，导致前置弹塑性金属短杆高速变形以致断裂，从而在输入杆中产生经滤波的拉伸方波脉冲。此方法所产生的拉伸方波脉冲平稳，高度和宽度可在较广范围内调节，以实现不同应变率、较大变形条件下的冲击拉伸试验。中应变率材料试验机则是通过高速液压驱动活塞杆进行预调速，再进行缓冲冲击加载，此外采用光学引伸计来测量试样的应变[16]。

不同应变率的拉伸试样形状类似，为平板哑铃状。其中动态拉伸试样平行段的长度和圆弧倒角的半径分别为6 mm和2 mm。准静态和中应变率拉伸试样，平行段比动态试样更长，为24 mm，从而减小试样端面效应，获得试验段更均匀的应变场。

2 结果与分析

2.1 TC11钛合金的力学性能

对TC11分别进行室温、应变率为0.001、0.01、0.05、4、18、210、450和940 s−1的单向拉伸试验，首先获得其工程应力应变曲线。每个应变率加载条件下至少进行3次试验，并根据体积不变假设，将工程应力−工程应变转化为真应力−真应变。

图1给出了不同应变率下的真应力−真应变曲线。从结果来看，TC11的拉伸应力−应变响应表现出典型的弹塑性变形特征以及明显的应变率敏感性。

由于TC11的拉伸应力−应变曲线并无明显的屈服点，将0.2%塑性应变量对应的流动应力作为该工况下的初始屈服应力。也对比了室温塑性应变量分别为0.01、0.02和0.03时的流动应力随应变率对数的变化关系曲线，具体如图2所示。从图2中可以明显看出：在1×10−3~1×103s−1跨越6个数量级的应变率范围内，初始屈服应力和流动应力随应变率的增大而增大，表现出明显的应变率强化效应。但是，两者与应变率对数之间并非简单的线性关系。为确切描述TC11拉伸力学行为的应变率敏感性，选择参数来表征室温时材料力学性能的应变率敏感程度：

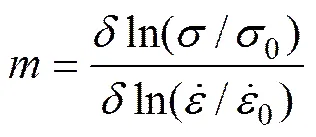
该参数的物理意义与Johnson-Cook模型中的应变率敏感参数类似，其中和分别是参考应变率和参考应变率下的流动应力。选取=0.001 s−1，利用式(1)计算出了不同应变率下初始屈服应力的应变率敏感参数值。在低应变率和高应变率，参数值分别约为0.013和0.028；中应变率区，参数的值则介于两者之间。以上结果均表明了高应变率加载时流动应力随应变率的增长速度明显高于准静态的，在中应变率区TC11表现出由应变率不太敏感向应变率敏感的转折过渡。一般认为金属的屈服行为是位错滑移或孪生变形引起，各滑移系对应的临界切应力与当前的位错组态等微结构密切相关。宫旭辉[6]在TC21拉伸力学行为的研究过程中发现了类似现象，为了解释材料的该类行为，进一步观察了不同应变率试样的位错组态。结果发现：高应变率下试样内的位错密度明显高于准静态加载，位错增殖速率的快速增大可能是引起高应变率下滑移系临界切应力以及屈服强度明显提高的主要原因。

此外，不同塑性应变量得到的流动应力和应变率对数关系曲线呈闭口形态，如图2所示。该结果表明，尽管流动应变表现出应变率强化的特征，但是随着应变率的增加，材料的塑性硬化规律逐渐减小，呈现出不同的应变率敏感性。该结果与Ti-6Al-4V动态压缩下的规律较为一致，KHAN等[3]和NEMAT-NASSER等[4]认为这现象可能与动态加载下的绝热温升软化效应有关。

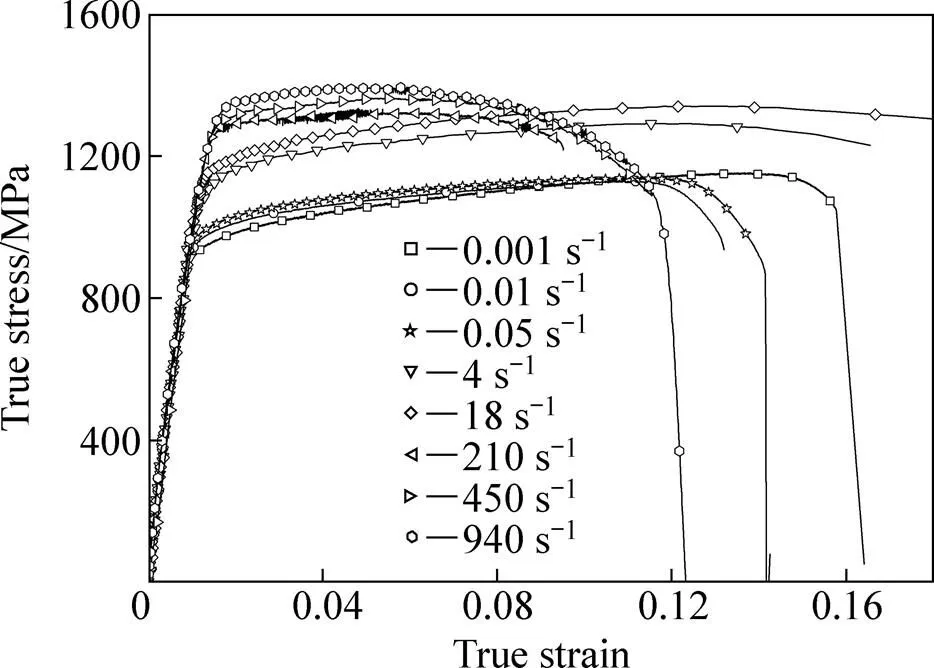
图1 TC11的真应力−真应变曲线

2.2 显微组织

利用金相显微镜观察了试件断口附近的金相组织。试验使用的是酸性腐蚀溶液，配方为(HF):(HNO3­):(H2O)=1:3:10。该配方与文献[1−3]一致，在酸性腐蚀液下，相腐蚀速率更快，因而在光学显微镜下腐蚀较深的相会呈现暗色，而腐蚀较浅的相为白色。

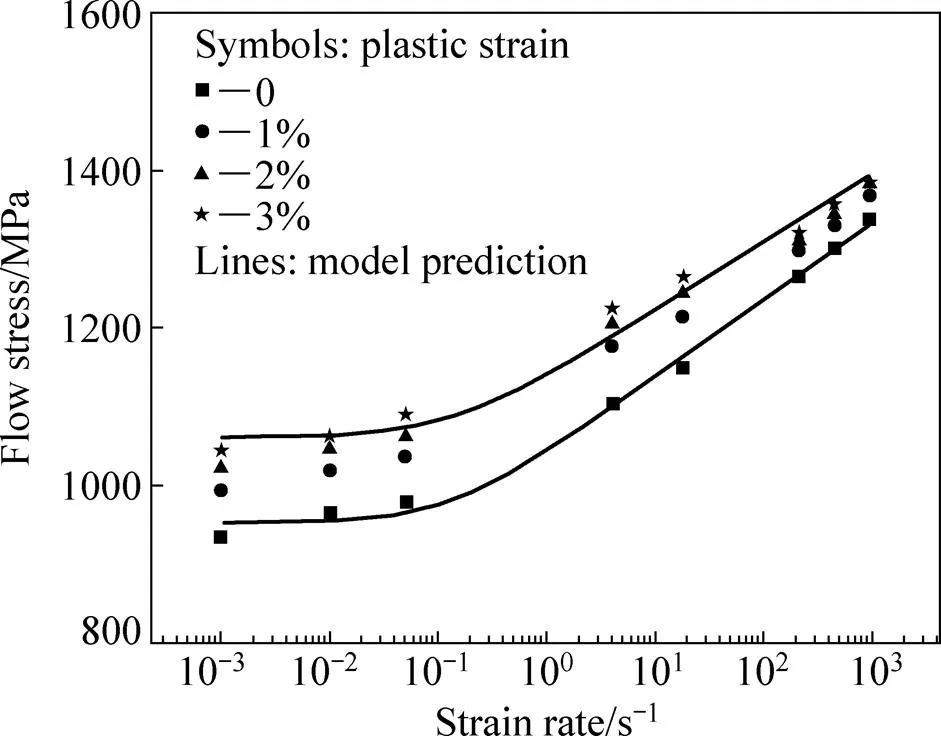
图2 不同塑性应变下流动应力和应变率对数关系

图3给出了变形前后的组织照片对比。从结果来看，初生相和+片层晶群均沿着加载方向表现出不同程度的拉伸变形，呈现出长条状，裂纹在初生相和+片层晶群内随机穿过。

为了进一步理解TC11在不同应变率下的失效机制，利用扫描电镜进行试样断口形貌观察，照片如图4和图5所示。不同应变率下的结果类似，断口呈现典型的韧窝形貌，根据形状和深浅不同分为：较深的等轴韧窝(区域)；较浅的韧窝(区域)；抛物状韧窝(区域)，三者分别对应了断口的纤维区、发射区和剪切唇。纤维区的韧窝大小随应变率变化并不明显。以上结果均表明在测试的应变率范围内TC11呈现出韧性断裂机制，该结果也与拉伸加载下材料具有较好的延展性相符。

图5 不同应变率下TC11的纤维区韧窝

3 本构模型

3.1 黏塑性流动法则

JOHNSON和COOK[19]于1983年提出了一个在较大应变、较宽温度和应变率范围内表征材料力学行为的唯象本构模型，并因形式简单，参数易于确定等优点，成为工程应用最为广泛的材料模型之一。为了便于动力学软件(如LS-Dyna和ABAQUS)实现结构动态响应规律的数值研究，利用Johnson-Cook模型对TC11不同应变率下的拉伸力学行为进行精确表征。在不考虑温度效应的情况下，材料的流动应力可表示为应变硬化和应变率强化效应相关函数的连乘，具体如下所示：

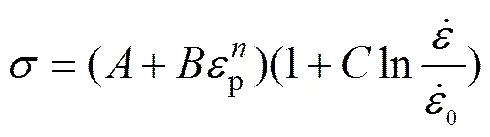
式中：为初始屈服强度；和为应变硬化系数；和分别是应变率敏感系数和参考应变率。

LIANG等[17]和XU等[18]分别对该模型的特点进行了充分研究，结果表明：JC模型所表征的材料应变硬化率随着应变率的增加而增大，呈现出应变硬化率与应变率对数线形强化的特征，即原始的JC模型并不能表征应变硬化率随加载应变率的增大而降低或者保持为常数的材料力学行为。

如前所述，TC11的拉伸力学行为呈现出明显的应变率相关性，但初始屈服应力和应变硬化行为对应变率的敏感程度并不相同，且在中应变率区呈现出流动应力对应变率不敏感向应变率敏感的转折过渡。鉴于以上分析，采用了一个修正的Johnson-Cook模型[14]来表征TC11的拉伸力学行为，如下所示：

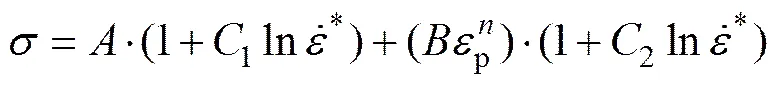
(4)

式中：1和2分别分别代表了初始屈服强度和应变硬化行为的应变率敏感性。为无量纲应变率；和分别为参考应变率和转折应变率。

与Johnson-Cook原始模型相比，新的本构模型作了两处修正：1) 分别使用了两组参数1和2分别表征应变率对初始屈服行为和应变硬化行为不同的影响规律；2) 引入转折应变率，以表征流动应力在中应变率范围内的转折现象。

3.2 数值验算

实际材料弹塑性变形是一个复杂的物理过程，数值计算分析也较为困难，涉及了屈服准则、流动法则、强化准则等多种理论和方法。以金属中最为常用的Mises屈服准则、等向硬化法则为例，给出了TC11钛合金的修正Johnson-Cook模型数值验算。

表1 模型的材料参数值

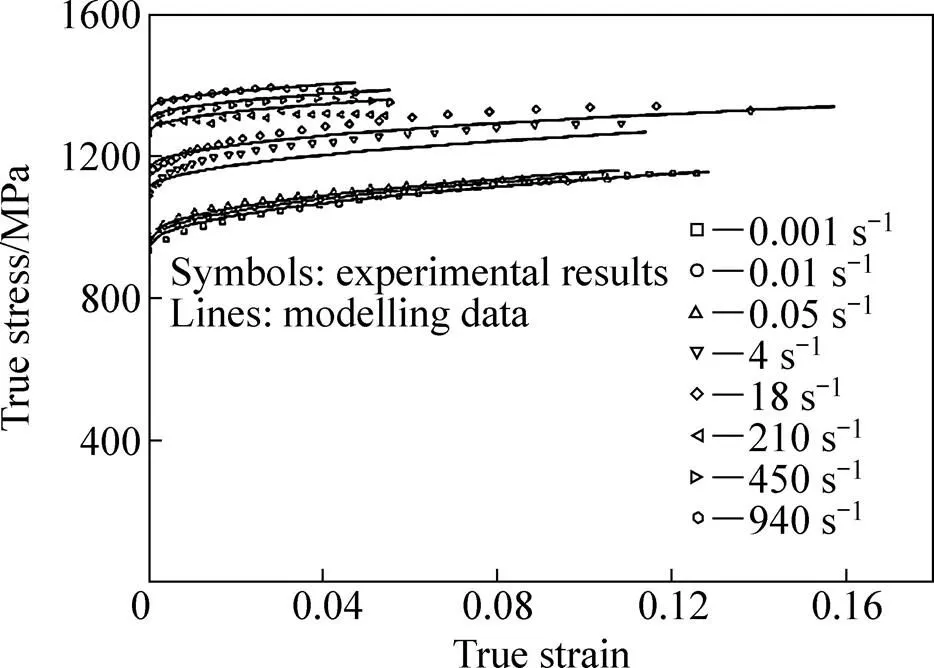
图6 模型表征结果和试验结果的对比

基于弹塑性独立假设，应变率张量是弹性应变率和塑性应变率的加法，即表示为

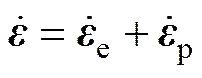
根据Hooker定律，各向同性材料的应力应变关系为

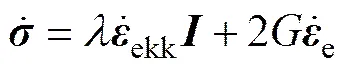
根据Drucker公设，发生塑性流动时的塑性应变率张量可以表示为

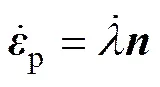
(8)

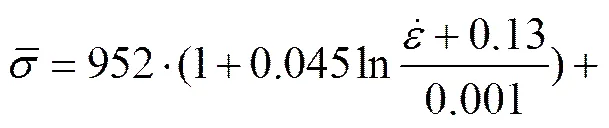
(9)

将上述方程写成增量形式，并采用弹性预测−塑性拉回的基本思想，编写与有限元软件ABAQUS接口匹配的用户子程序UMAT。在材料用户子程序编写过程中，首先由一组首先计算+Δ时刻的试应力，倘若试应力满足Mises屈服条件，则计算该分析步的等效塑性应变增量，进而得到该分析步的塑性应变增量和弹性应变增量，最终计算出+Δ时刻的应力张量。

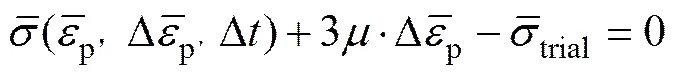
采用上述材料用户模型对TC11钛合金拉伸试样在不同应变率下的力学响应进行了数值模拟。考虑到对称性，只需建立1/8对称模型，其中拉伸端施加速度边界条件，以模拟不同工况的加载条件。模拟结束后，输出两个端面的相对距离变化量和端面拉力大小来分别计算试样的平均应变和应力。

不同应变率下的模拟结果与试验结果对比如图7和图8所示。从结果来看，无论是连续加载还是复杂的应变率跳跃加载，模拟结果和试验结果均吻合较好，表明所建立的本构模型及其用户子程序较好地应用于TC11应变率相关力学行为的数值仿真。

需要注意的是，本研究并未考虑高应变率下的热力耦合效应。对于金属材料而言，高应变率加载下应力应变响应是应变硬化效应、应变率强化效应以及温度软化效应三者相互竞争的结果。为了更加精确地表征高应变率下绝热温升软化效应对材料力学行为的影响，需要进一步测量动态加载条件下的绝热温升以及获得高应变率下的等温应力应变曲线。

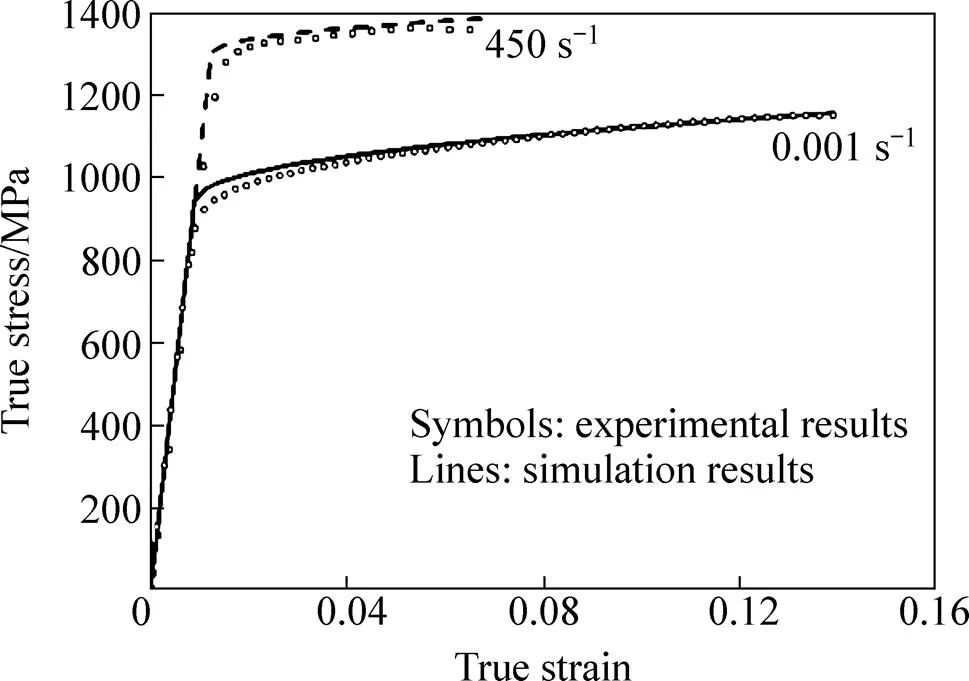
图7 不同应变率下的模拟结果

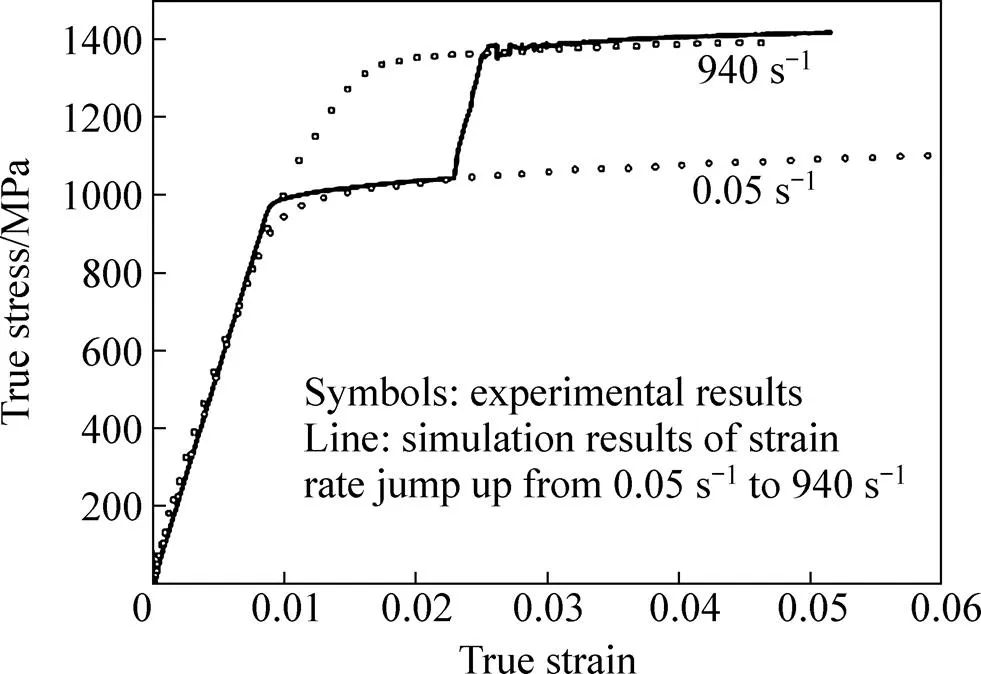
图8 应变率跳跃加载下的模拟结果

4 结论

1) TC11钛合金在拉伸下的初始屈服应力随应变率的提高而增大，呈现应变率强化效应，在中应变率范围内呈现出应变率不太敏感向应变率敏感的转折现象，材料的应变硬化率随着应变率的提高而逐渐降低。

2) 提出的修正Johnson-Cook模型，计算了应变率对初始屈服应力和应变硬化行为的不同影响。基于有限元软件ABAQUS平台所编写的修正模型的材料用户子程序，进行不同应变率下拉伸力学行为的数值计算，所获得的计算结果与试验结果吻合较好，表明建立的本构模型和用户子程序能够较好地应用于TC11钛合金应变率相关力学行为的工程数值仿真。

REFERENCES

[1] SHI Zhi-feng, GUO Hong-zhen, LIU Rui, WANG Xiao-chen, YAO Ze-kun. Microstructure and mechanical properties of TC21 titanium alloy by near-isothermal forging[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(1): 72−79.

[2] 古 一, 戚延龄, 夏长清, 李学雄, 王志辉. 热暴露对TC11 钛合金组织和力学性能的影响[J]. 中国有色金属学报, 2013, 23(4): 997−1004. GU Yi, QI Yan-ling, XIA Chang-qing, LI Xue-xiong, WANG Zhi-hui. Effects of thermal exposure on microstructure and mechanical properties of TC11 titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(4): 997−1004.

[3] KHAN A S, KAZMI R, FARROKH B, FARROKH B, ZUPAN M. Effect of oxygen content and microstructure on the thermo-mechanical response of three Ti-6Al-4V alloys: Experiments and modeling over a wide range of strain-rates and temperatures[J]. International Journal of Plasticity, 2007, 23(7): 1105−1125.

[4] NEMAT-NASSER S, GUO W G, NESTERENKO V F, INDRAKANTI S S, GU Y B. Dynamic response of conventional and hot isostatically pressed Ti-6Al-4V alloys: Experiments and modeling[J]. Mechanics of Materials, 2001, 33(8): 425−439.

[5] 周 舸, 丁 桦, 曹富荣, 赵文娟, 侯红亮, 李志强. TC21 合金的热压缩变形行为及变形机理[J]. 中国有色金属学报, 2011, 21(9): 2111−2118.ZHOU Ge, DING Hua, CAO Fu-rong, ZHAO Wen-juan, HOU Hong-liang, LI Zhi-qiang. Hot compression deformation and deformation mechanisms of TC21 alloy[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(9): 2111−2118.

[6] 宫旭辉. 高温环境下+钛合金的动态拉伸力学行为——测试、分析与表征[D]. 合肥: 中国科学技术大学，2010.GONG Xu-hui. Dynamic tensile behavior of+titanium alloys at elevated temperatures-test, analysis and description[D]. Hefei: University of Science and Technology of China, 2010.

[7] 张长清, 谢兰生, 陈明和, 商国强. 高应变率下 TC4-DT钛合金的动态力学性能及塑性本构关系[J]. 中国有色金属学报, 2015, 25(2): 323−329. ZHANG Chang-qing, XIE Lan-sheng, CHEN Ming-he, SHANG Guo-qiang. Dynamic mechanical property and plastic constitutive relation of TC4-DT Ti alloy under high strain rate[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 323−329.

[8] 杨 扬, 曾 毅, 汪冰峰. 基于 Johnson-Cook 模型的TC16 钛合金动态本构关系[J]. 中国有色金属学报, 2008, 18(3): 505−510.YANG Yang, ZENG Yi, WANG Bing-feng. Dynamic constitutive relationship of TC16 titanium alloy based on Johnson-Cook model[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(3): 505−510.

[9] ZHANG B, LEI L M, JIANG X L, SONG Z M, HUANG X, ZHANG G P. On temperature and strain rate dependent strain localization behavior in Ti-6.5Al-3.5Mo-1.5Zr-0.3Si alloy[J]. Journal of Materials Science and Technology, 2013, 29(3): 273−278.

[10] LIU G F, ZHANG S Z, CHEN L Q. Hot deformation behavior of Ti-6.5Al-3.5Mo-1.5Zr-0.3Si alloy with acicular microstructure[J]. Journal of Central South University of Technology, 2011, 18(2): 296−302.

[11] HUANG L J, GENG L, ZHENG P Q, LI A B, CUI X P. Hot tensile characterization of Ti-6.5Al-3.5Mo-1.5Zr-0.3Si alloy with an equiaxed microstructure[J]. Materials and Design, 2009, 30(3): 838−841.

[12] ZHANG X Y, LI M Q, LI H, LUO J, SU S B, WANG H. Deformation behavior in isothermal compression of the TC11 titanium alloy[J]. Materials and Design, 2010, 31(6): 2851−2857.

[13] LEI L, HUANG X, WANG M, WANG L, QIN J, LU S. Effect of temperature on deformation behavior and microstructures of TC11 titanium alloy[J]. Materials Science and Engineering: A. 2011, 528(28): 8236−8243.

[14] WANG Y, ZHOU Y X, XIA Y M. A constitutive description of tensile behavior for brass over a wide range of strain rates[J]. Materials Science and Engineering A, 2004, 372(1): 186−190.

[15] 汪 洋, 夏源明. 杆杆型冲击拉伸试验装置一维试验原理有效性的论证[J]. 实验力学, 1997, 12(1): 126−134.WANG Yang, XIA Yuan-ming. The proof of one-dimensional experimental principle for bar-bar tensile impact apparatus[J]. Experimental Mechanics, 1997, 12(1): 126−134.

[16] 吴衡毅, 马 钢, 夏源明. PMMA低、中应变率单向拉伸力学性能的实验研究[J]. 实验力学, 2005, 20(2): 193−199. WU Heng-yi, MA Gang, XIA Yuan-ming. Experimental study on mechanical properties of PMMA under unidirectional tensile at low and intermediate strain rates[J]. Experimental Mechanics, 2005, 20(2): 193−199.

[17] LIANG R, KHAN A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures[J]. International Journal of Plasticity, 1999, 15(9): 963−980.

[18] XU Z, HUANG F L. Comparison of constitutive models for FCC metals over wide temperature and strain rate ranges with application to pure copper[J]. International Journal of Impact Engineering, 2015, 79(1): 65−74.

[19] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//Proceedings of 7th International Symposium on Ballistics. Hague.1983: 541−547.

(编辑 王 超)

Experiment and constitutive model of rate-dependent behavior of titanium alloy TC11

ZHANG Jun1, WANG Yang2, WANG Yu2

(1. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China;2. CAS Key Laboratory of Mechanical Behavior and Design of Materials,Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China)

The MTS809 machine, moderate strain-rate testing setup and the split hopkinson bar system were adopted to conduct uni-axial tension tests of TC11 at strain rates ranging from 1×10−3s−1to 1×103s−1. Theobservation of microstructure and the fracture morphology was carried out via the optical microscope and SEM. A modified Johnson-Cook model was proposed to predict the mechanical behavior. Experimental results indicate that there is a positive strain-rate sensitivity with respect to the initial yield behavior. However, the transition of rate dependent sensitivity is presented at the moderate-rate loading conditions. Thegrains and+colonies are stretched along the tension direction and break in a manner of ductile fracture. The modified Johnson-Cook constitutive model incorporates the different strain rate effects on the yield stress and strain hardening behavior. Excellent agreement between the experimental data and model predication indicates that such model is suitable for the rate-dependent numerical simulation of titanium alloy TC11.

titanium alloy; strain rate; constitutive model

Project (11172288) supported by National Nature Science Foundation of China

2016-05-26; Accepted date: 2016-11-11

ZHANG Jun; Tel: +86-816-2482494; E-mail: hjzhangj@caep.cn

10.19476/j.ysxb.1004.0609.2017.07.07

1004-0609(2017)-07-1369-07

O347

A

国家自然科学基金项目(11172288)

2016-05-26；

2016-11-11

张 军，助理研究员，博士；电话：0816-2482494；E-mail：hjzhangj@caep.cn