热虹吸管相变传热行为CFD模拟

王啸远，朱跃钊，陈海军，王银峰，范红途



热虹吸管相变传热行为CFD模拟

王啸远，朱跃钊，陈海军，王银峰，范红途

(南京工业大学机械与动力工程学院，江苏南京，211816)

基于VOF模型和改进的相变模型对热虹吸管稳态相变传热过程进行CFD模拟，根据温度分布实验数据和可视化实验进行验证，并分析充液率对热管蒸发−冷凝传热行为的影响。研究结果表明：CFD模型能够较准确地描述热管工质的蒸发和冷凝过程，模拟得到热管各段均温的最大偏差为10.2 K，相对误差2.9%，采用改进的相变模型，温度分布模拟值与实验值一致性更好；模拟得到蒸发段工质流型转变过程与可视化实验定性相符；热管冷凝段以膜状冷凝传热为主，充液率的改变对其影响不大，充液率主要影响蒸发段的传热行为，进而影响热管的传热性能。该工作有助于对热管运行机理的理解，并为其CFD模拟提供指导。

热虹吸管；相变传热；CFD；可视化

两相闭式热虹吸管(简称热虹吸管)，是依靠重力回流冷凝液的高效传热元件，具有超高的导热性以及优良的等温性，更兼结构简单和工作可靠的优点[1]，在太阳能中高温热利用[2]、聚光光伏发电[3]、余热回收[4−5]、以及电子元器件[6]的高效散热等领域具有潜在的价值。热管通过内部工质的相变循环过程进行传热，传热机理较为复杂[1, 7−8]。对于热虹吸管的传热行为研究，传统的数值模拟方法往往忽略了工质的沸腾和流动，因此，与实际过程偏差较大。特别是对于压力较高的工质(如氨)或者高温热管工质(如钠)，这类热管的启动和相变传热行为研究缺乏有效的可视化实验研究手段，更难直观分析相变传热机理。CFD模拟技术可直观地展现工质的相变和流动状态，有助于热管运行机理和传热行为的深入理解。SCHEPPER等[9]提出了稳态沸腾过程的CFD相变模型，随后，学者们分别基于该模型利用Fluent软件对以水为工质热管的传热性能[10]、管壁温度分布[11]以及纳米流体的强化传热作用[12]进行了模拟研究，但总的来说，热管相变传热过程的CFD模拟研究不多。此外，现有热管CFD模拟研究[10−12]采用的相变模型是针对稳态沸腾过程提出的，较难适应热管内蒸发−冷凝共存的相变传热特征，模拟偏差较大，同时，模拟性能缺乏实测可视化现象的验证。本文作者拟以ANSYS Fluent 14.5软件为平台，对 Schepper相变模型进行改进，建立热管CFD模型，模拟热管的相变传热行为，结合温度分布实验数据和可视化实验现象对模拟结果进行较全面的验证，并根据模拟结果深入分析不同充液率下热管的相变传热行为。

1 模型建立及求解

1.1 几何模型

热管工质以轴向和径向流动为主，而不是旋转流动，故计算域可简化为二维几何模型。采用Gambit 2.4建立耦合固体管壁与汽液流场的铜−水热管几何模型，尺寸参照文献[13]，总长980 mm，内径为25 mm，壁厚3 mm，蒸发段、绝热段和冷凝段长度分别为295，305和380 mm。

1.2 CFD模型

基于ANSYS Fluent 14.5建立热管的CFD模型，假设条件如下：1)相变过程压力恒定，饱和温度sat为定值；2) 汽液相及管壁物性参数均为常数；3) 忽略汽液界面剪切力；4) 汽液流动均为层流。

建立的热管CFD模型采用VOF多相流模型[14]处理工质的流动与传热过程，通过CSF(continuum surface force)模型[15]引入表面张力的影响，并对Schepper相变模型进行了改进。

1.2.1 VOF模型

常用多相流模拟方法有欧拉−拉格朗日法和欧拉−欧拉法2种[11]。欧拉−拉格朗日法将主相处理为连续相，其余相作为离散颗粒追踪计算，仅适用于颗粒流问题的模拟。对于包含大汽泡流和分层流的热管模拟，应采用将各相均视为连续相的欧拉−欧拉法。VOF模型是欧拉−欧拉法的一种，其特有的相体积率几何重构算法能够精确追踪汽液界面的迁移，实现相变过程热质传递现象的模拟[10]。

VOF模型主要对连续性方程、动量方程和能量方程三大控制方程进行求解。由于热管流场区域仅有汽液两相，同一计算单元内两相相体积率之和为1，故连续性方程仅对液相进行求解，而动量方程与能量方程均针对汽液混合相而言，控制方程及混合相各物性参数的计算方法见式(1)~(7)。

连续性方程：

动量方程：

(2)

能量方程：

混合相物性参数计算方法：

(4)

(6)

(7)

1.2.2 相变模型

热管的高效传热特性源于腔内工质的相变传热循环，因此，相变的模拟至关重要。工质相变过程可简化描述为质量和能量的转移，求解控制方程时实时修改质量和能量方程的源项即可实现其模拟。源项的修改通过UDF(user-defined function)功能实施，即通过C语言将源项表达式编译导入ANSYS Fluent 14.5求解器中，使其与控制方程相关联。

SCHEPPER等[9]提出的稳态相变模型如下式 所示。

蒸发过程(≥sat)：

(9)

(10)

冷凝过程(＜Tsat)：

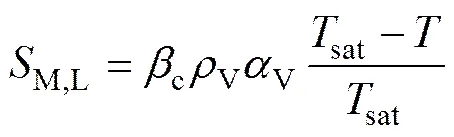
(12)

(13)

式中：e和c分别为蒸发和冷凝过程的时间松弛因子；sat为饱和温度；Δ为汽化潜热。从式(8)~(13)可知：当高于sat时为蒸发过程，计算单元内液相质量减少，汽相增加，显热相应转化为潜热；当低于sat时为冷凝过程，热质传递方向恰好与蒸发过程相反。

e和c分别控制工质的蒸发和冷凝速率，SCHEPPER等[9]在稳态沸腾过程的模拟研究中均取0.1 s−1，显然，热管模拟直接套用该模型，稳态阶段蒸发和冷凝过程的热质传递量将难以达到平衡。因此，本文利用UDF功能对c进行修正，促使蒸发和冷凝过程趋于平衡，修正公式见式(14)，模拟中e保持为0.1不变，c初始值取0.1。

式中：下标表示时间步长数；e和c分别为蒸发和冷凝过程的质量传递总量。

热管稳态运行阶段，蒸发段工质处于核态沸腾状态，沸腾过热度可由下式[16]求得：

考虑到管壁的热传导过程，则sat取值为

式中：e为实测蒸发段均温；o和i分别为热管外径和内径；为管壁热导率；e为蒸发段长度；为输入功率。

1.2.3 CSF模型

表面张力是液体表面分子引力不均衡而产生的沿表面作用的张力，可使汽泡或液滴的表面积趋于最小，降低表面自由能。因此，表面张力对汽泡运动以及工质的润湿特性具有重要影响。本文通过引入CSF模 型[15]修改动量源项来模拟表面张力作用，该源项如下式所示：

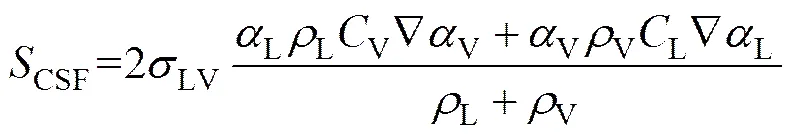
式中：为表面曲率。

1.3 边界条件及求解策略

根据文献[13]的实验条件，热管蒸发段为恒功率电加热，冷凝段为水冷。故模拟时蒸发段施加恒热流密度进行加热，冷凝段采用水的对流换热，输入热流密度、冷却水温度及对流换热系数的取值均由实验条件而定，绝热段设为绝热壁面，即热流密度为0。

能量方程与动量方程均以二阶迎风格式离散，相体积率和压力的插值分别采用几何重构法和PRESTO法，速度与压力耦合关系由SIMPE算法处理。

计算域初始化温度和压力分别为298 K和1.72 kPa，热管充液率R(工质体积与蒸发段容积之比)通过patch功能设置。动量方程与连续性方程的残差收敛标准设为10−4，能量方程为10−7。计算初期，时间步长取1×10−5s，随模拟时间增加而逐步提高至5×10−4s。当热管蒸发段输出功率与输入功率达到平衡时认为热管达到稳态，计算完成。

1.4 网格独立性验证

为得到网格独立性的解，本文对R为0.6的热管进行考核，计算网格数分别取25 670，39 640，58 410和85 420。网格划分采用四边形结构化网格，热管内壁边界层经加密处理，如图1所示。图2所示为热管稳态工作温度w在不同网格数下的模拟结果。从图2可知：w随网格数增多趋于定值，当网格数目高于 58 410时，网格数对w的影响可忽略，因此，本文计算网格数取58 410。

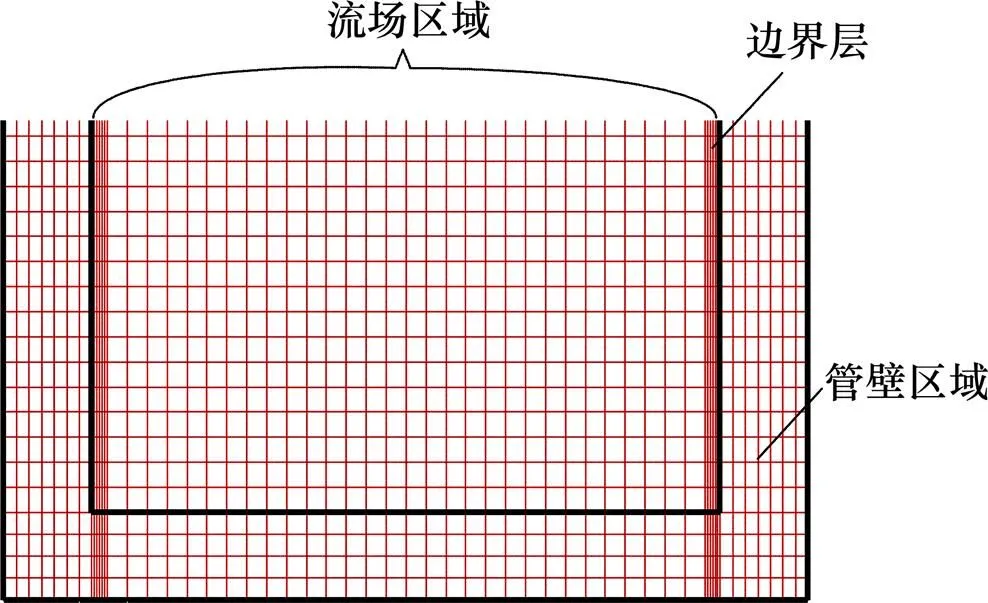
图1 网格划分示意图

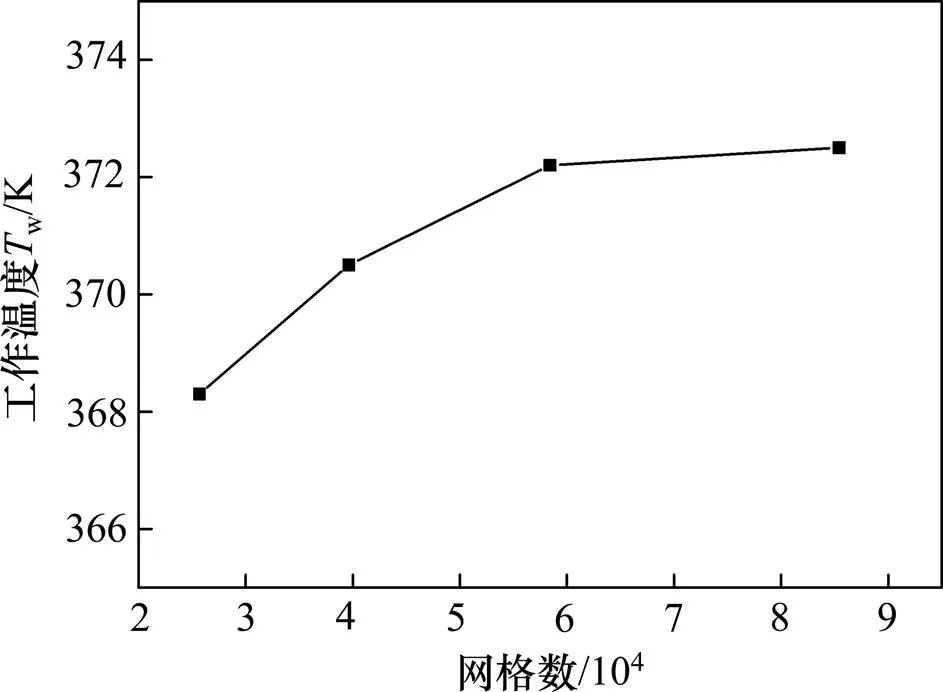
图2 网格独立性考核

2 可视化实验

建立的热管可视化实验平台如图3所示。热管由全玻璃制成，其尺寸与文献[13]中相同。实验中热管蒸发段以水浴加热，冷凝段为玻璃夹套水冷，绝热段和水冷夹套外用保温棉绝热。通过加热温度和冷却条件调整热管的工作温度，使其运行状态接近文献[13]所述工况，并利用高速相机(D7000 日本尼康)记录稳态工况下热管蒸发段的沸腾现象，与模拟结果对比 验证。

为确保良好的可视化观测效果，将可视化热管蒸发段浸没在圆柱形玻璃水槽水浴中，但这样增加了有效壁温分布测定的难度，因此，本文未对该可视化热管的温度分布进行模拟对比。

图3 可视化热管及实验平台

3 结果与讨论

3.1 模型验证

3.1.1 温度分布验证

表1列出加热功率670 W条件下不同充液率热管蒸发段、绝热段和冷凝段稳态均温的实验值[13]与模拟值。从表1可以看出：冷凝段模拟值与实验值的偏差最大，最大偏差为10.2 K(相对偏差2.9%)，原因在于实验所测温度为冷凝夹套外壁温度，而模拟值为热管管壁温度。但是，蒸发段和绝热段的模拟与实验值的相对偏差均在2.1%以内，远低于FADHL等[11]的模拟偏差，可见相变模型的改进对模拟结果准确性的改善作用明显，温度分布模拟值与实测值的吻合度更高。

3.1.2 流型定性验证

在热管管壁温度分布定量验证的基础上，进一步对相变流动行为作可视化定性验证。由表1可知：在文献[13]测试工况下，R为0.3或0.9时热管工作温度均大于373 K，受水浴加热温度限制，本文仅针对充液率R为0.6的热管进行了可视化实验和模拟流型的定性验证。图4所示为热管(R=0.6)蒸发段稳态流型CFD模拟结果与可视化现象的对比，模拟时加热功率为670 W。从图4可知：可视化实验直观地展现了蒸发段汽泡长大脱离壁面后的合并、失稳和破碎现象，即流型从泡状流、栓塞流向环状流的演变过程，热管CFD模型较准确地预测了该流型转变，与实验结果基本相符。模拟偏差产生的主要原因可能是热管CFD模拟蒸发段采用的恒热流密度边界条件与可视化实验中的对流换热存在差异。

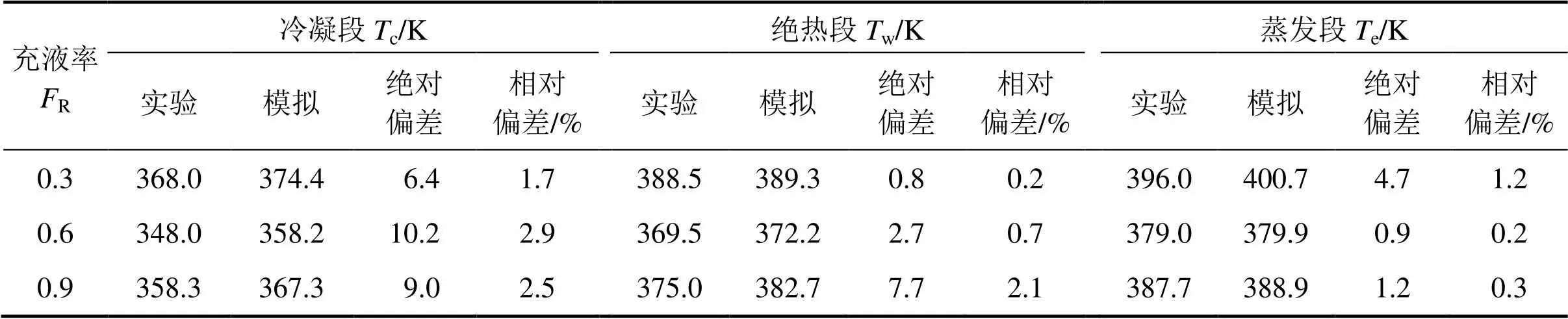
表1 热管各段均温实验值与模拟值

图4 蒸发段流型对比(FR=0.6)

3.2 充液率对热管相变传热行为的影响

3.2.1 汽液两相分布

工作温度可定性反映热管的运行状态，在相同的传输功率下，工作温度越低，意味着热管内工质的传热循环效率越高，热管整体传热性能越好。表1所示热管实测温度显示：充液率对w有显著影响，R为0.6时w最低，充液率的增大或降低均会引起w的升高，因此，测试条件下热管最佳充液率为0.6。

热管内工质的流动传热行为与充液率密切相关，为进一步揭示充液率对热管传热性能的影响，有必要对管内流型进行分析。图5所示为稳态工况下，不同充液率热管(R为0.3，0.6和0.9)内两相分布的模拟结果。从图5可以看出：在不同充液率下，热管冷凝段均为膜状冷凝换热，充液率的改变主要影响蒸发段的传热行为。对于R为0.3的热管，液池区域为核态沸腾，但液池仅占据蒸发段底部小部分区域，回流液膜在蒸发段上部出现了间断。R为0.6条件下，液池略高于蒸发段出口，蒸发段内壁完全润湿，有效沸腾换热面积增大，热管处于较佳运行状态，工作温度最低。而当R达到0.9时，蒸发段大量上浮的汽泡将工质液面托至绝热段，同时，蒸发段还观察到成片的膜状汽泡，表明蒸发段传热条件恶化。

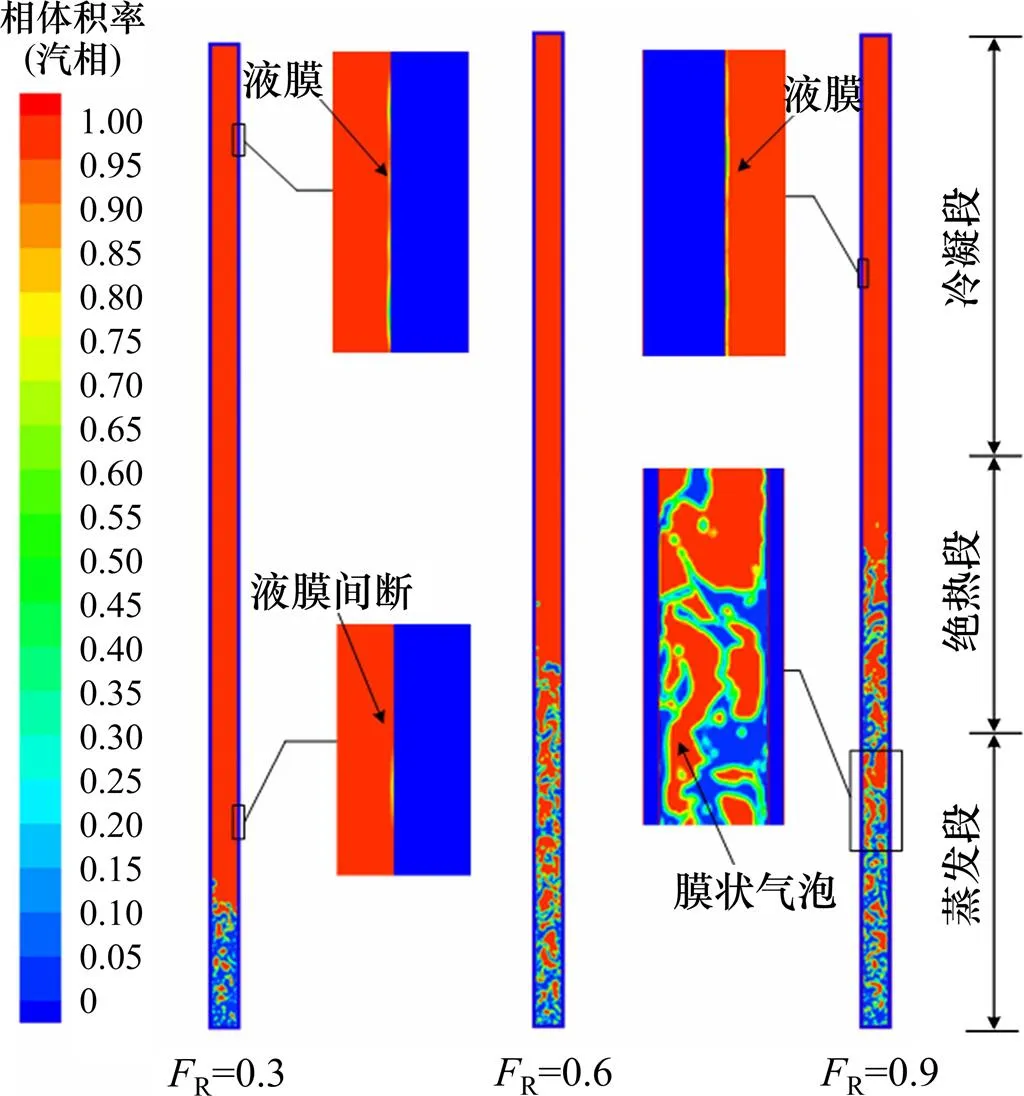
图5 不同充液率热管两相分布

3.2.2 温度和速度分布

通过对热管温度分布和工质流动的分析可进一步了解充液率对热管相变传热行为的影响。不同充液率下热管管壁温度分布以及管内轴线温度和工质流速分布如图6所示。从图6(a)可以看出：充液率较低时(R为0.3)，热管蒸发段上部形成了局部高温区，并且，管内轴向均温性较差。由图5可知：由于充液率较低，热管蒸发段上部无液池浸润，为不连续的液膜蒸发传热，换热系数远低于液池区域的核态沸腾传热，致使局部高温的形成。蒸发段的局部干涸又导致蒸汽产生一定的过热度以及蒸发段出口蒸汽温度的振荡，造成管内轴向均温性较差。

由图6(b)和(c)可知：增大充液率有利于改善热管管壁和管内的温度分布，然而，充液率的增大为汽泡的发育提供了更多的空间，汽泡脱离液面的速度也急剧增大。相比于R为0.3的热管，R为0.6和0.9时热管蒸发段液面处工质流速从1.5 m/s增加至4.5 m/s左右。另一方面，R为0.6，热管内工质最大流速点恰好处于蒸发段出口，而当R增大至0.9时，液池液面则提升至绝热段，绝热段流速较大的工质团将阻碍冷凝液及时回流至蒸发段，这也是其工作温度相对较高的原因之一。

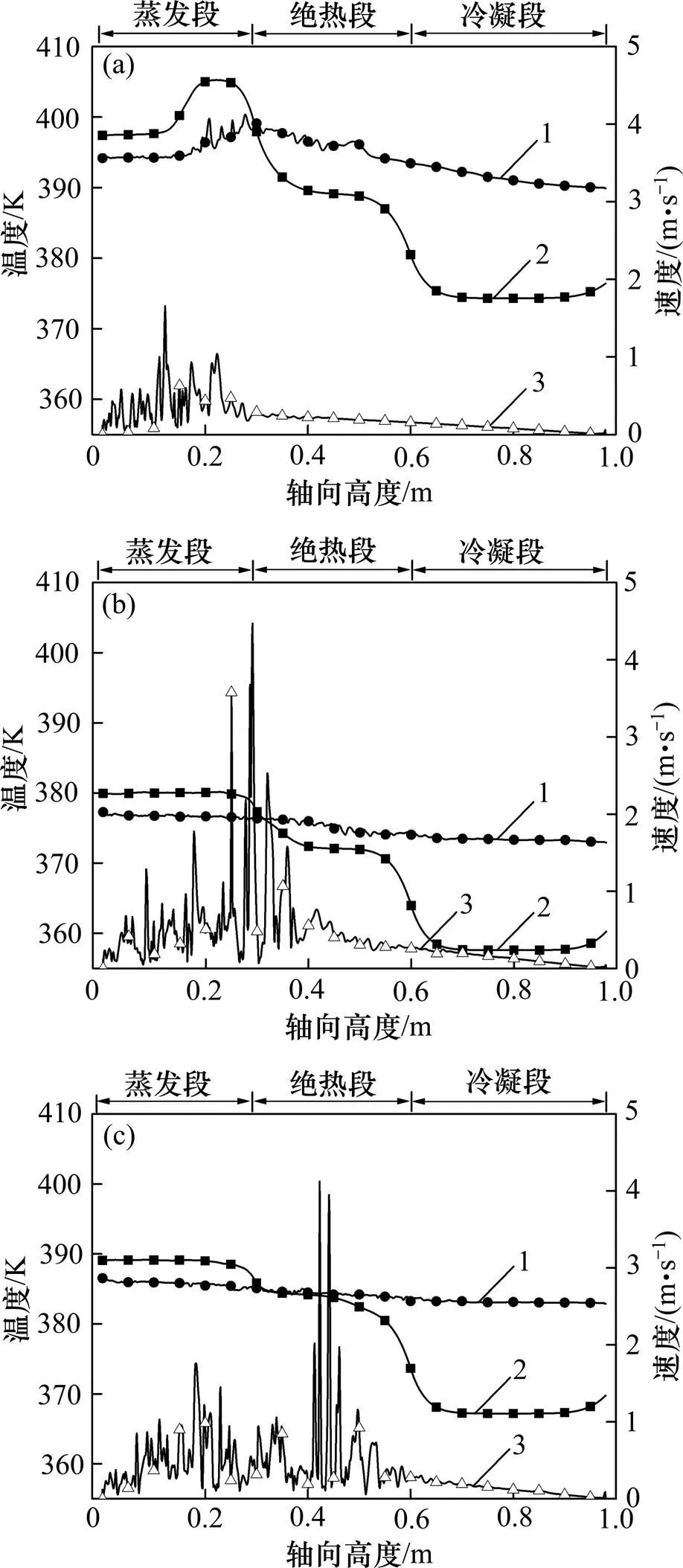
FR：(a) 0.3；(b) 0.6；(c) 0.9

从图6还可发现：不同充液率条件下热管冷凝段上部均出现了温度回升现象，这与ALIZADEHDAKHEL等[10]在实验中观察到的现象相符，其原因在于，冷凝段顶端冷凝液膜最薄，热阻较低，液膜在下降过程中逐渐增厚，热阻增大，故冷凝段顶端换热系数高于其余区域，管壁温度出现回升。

4 结论

1) 热管管壁温度分布模拟值与实验值具有较好的一致性，各段均温的最大偏差为10.2 K，相对误差2.9%，采用改进的相变模型，模拟结果准确度更高，同时，模拟得到蒸发段工质流型从泡状流、栓塞流向环状流的转变过程，与可视化实验定性相符，模型能够较好地预测热管内工质沸腾与冷凝回流的传热行为。

2) 热管冷凝段均为膜状冷凝，充液率的改变主要影响热管蒸发段的相变传热行为：充液率过小易导致蒸发段局部干涸过热，均温性恶化，过大则形成膜状沸腾，抬高工质液面，阻碍冷凝液回流。推荐的热管充液率为0.6，其液面高度与蒸发段高度持平，传热性能优良。

[1] 庄骏, 张红. 热管技术及其工程应用[M]. 北京: 化工工业出版社, 2000: 67.ZHUANG Jun, ZHANG Hong. Heat pipe technology and engineering application[M]. Beijing: Chemical Industry Press, 2000: 67.

[2] LIU Zhenhua, HU Renlin, LU Lin, et al. Thermal performance of an open thermosyphon using nanofluid for evacuated tubular high temperature air solar collector[J]. Energy Conversion and Management, 2013, 73(5): 135−143.

[3] 王子龙, 张华, 张海涛. 聚光光伏系统热管散热器运行特性的优化[J]. 太阳能学报, 2012(6): 986−992. WANG Zilong, ZHANG Hua, ZHANG Haitao. Optimization of operation characteristics for finned heat pipe radiator in concentrating photovoltaic system[J]. Acta Energiae Solaris Sinica, 2012(6): 986−992.

[4] JOUHARA H, MERCHANT H. Experimental investigation of a thermosyphon based heat exchanger used in energy efficient air handling units[J]. Energy, 2012, 39(1): 82−89.

[5] CIEŚLIŃSKI J T, FIUK A. Heat transfer characteristics of a two-phase thermosyphon heat exchanger[J]. Applied Thermal Engineering, 2013, 51(S1/S2): 112−118.

[6] TSAI T E, WU H H, CHANG C C, et al. Two-phase closed thermosyphon vapor-chamber system for electronic cooling[J]. International Communications in Heat and Mass Transfer, 2010, 37(5): 484−489.

[7] 辛公明, 张鲁生, 王鑫煜, 等. 自湿润流体内螺纹重力热管传热特性[J]. 工程热物理学报, 2013, 34(12): 2363−2365. XING Gongming, ZHANG Lusheng, WANG Xinyu, et al. Heat transfer characteristics of internal helical micro fin gravity heat pipe with self-rewetting fluid[J]. Journal of Engineering Thermophysics, 2013, 34(12): 2363−2365.

[8] 曲伟, 王焕光. 高温及超高温热管的相容性和传热性能[J]. 化工学报, 2011, 62(S1): 77−81. QU Wei, WANG Huangguang. Compatibility and heat transfer of high and super high temperature heat pipes[J]. Journal of Chemical Industry and Engineering (China), 2011, 62(S1): 77−81.

[9] SCHEPPER S C K D, HEYNDERICKX G J, MARIN G B. Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker[J]. Computers and Chemical Engineering, 2009, 33(1): 122−132.

[10] ALIZADEHDAKHEL A, RAHIMI M, ALSAIRAFI A A. CFD modeling of flow and heat transfer in a thermosyphon[J]. International Communications in Heat and Mass Transfer, 2010, 37(3): 312−318.

[11] FADHL B, WROBEL L C, JOUHARA H. Numerical modelling of the temperature distribution in a two-phase closed thermosyphon[J]. Applied Thermal Engineering, 2013, 60(1/2): 122−131.

[12] ASMAIE L, HAGHSHENASFARD M, MEHRABANI- ZEINABAD A, et al. Thermal performance analysis of nanofluids in a thermosyphon heat pipe using CFD modeling[J]. Heat Mass Transfer, 2013, 49(5): 667−678.

[13] NOIE S H. Heat transfer characteristics of a two-phase closed thermosyphon[J]. Applied Thermal Engineering, 2005, 25(4): 495−506.

[14] HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201−225.

[15] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335−354

[16] REAY D A, KEW P A. Heat pipes[M]. 15th ed. Oxford: Butterworth-Heinemann, 2006: 65.

(编辑 陈爱华)

CFD modeling of phase change heat transfer behaviors in thermosyphons

WANG Xiaoyuan, ZHU Yuezhao, CHEN Haijun, WANG Yinfeng, FAN Hongtu

(School of Mechanical and Power Engineering, Nanjing Tech University, Nanjing 211816, China)

A computational fluid dynamic (CFD) model based on the volume of fluid (VOF) multiphase model and an improved phase change model were developed to simulate the phase change heat transfer process in thermosyphons at steady state, and the modeling results were validated by measuring wall temperature distribution and visualization experiments. Besides, the influence of filling ratio (FRs) on the evaporation-condensation behavior in thermosyphons was analyzed. The results show that this CFD model can reproduce both the vaporization and condensation processes well. The predicted temperature distribution show better consistency with experimental results using the improved phase change model, the maximum deviation of average temperature at different sections being 10.2 K with a relative deviation of 2.9%. Furthermore, the predicted flow regimes are generally in agreement with the observed phenomenon in visualization testing. Filmwise condensation is the main heat transfer mode at condenser area in thermosyphons which is not affected by FRs. However, the variation of FRs considerably affects the heat transfer behavior at evaporator and thus changes the heat transfer performance of thermosyphons. This study is conducive for understanding the operating mechanism of thermosyphons and meanwhile provides some guidance for its CFD modeling.

thermosyphon; phase change heat transfer; computational fluid dynamic (CFD); visualization

10.11817/j.issn.1672-7207.2017.05.035

TK172.4

A

1672−7207(2017)05−1391−07

2016−07−21；

2016−09−09

国家自然科学基金资助项目(51276086)；国家科技支撑计划项目(2014BAJ01B06) (Project(51276086) supported by the National Natural Science Foundation of China; Project(2014BAJ01B06) supported by the National Science and Technology Support Program of China)

朱跃钊，博士，教授，博士生导师，从事热科学与工程等研究；E-mail: zyz@njtech.edu.cn