高压引水隧洞运行期复杂承载过程数值分析

邓建，肖明，陈俊涛



高压引水隧洞运行期复杂承载过程数值分析

邓建1, 2，肖明1, 2，陈俊涛1, 2

(1. 武汉大学水资源与水电工程科学国家重点实验室，湖北武汉，430072；2. 武汉大学水工岩石力学教育部重点实验室，湖北武汉，430072)

基于引水隧洞运行期受力机制，将运行期全过程分为3个阶段：钢衬单独承载，初始缝隙闭合阶段；衬砌未开裂，衬砌与围岩复杂接触联合承载阶段；衬砌开裂，内水外渗阶段。针对各阶段力学特性，分别提出钢衬单独作用弹性荷载求解方法、基于接触力法的衬砌与围岩联合承载分析方法以及考虑应力和损伤影响的渗透系数与渗透荷载计算方法。并据此编制三维有限元计算程序，对某引水隧洞运行期全过程进行数值模拟。研究结果表明：工程实例计算结果较为合理地反映高内水压力下引水隧洞运行期全过程受力特性，并为水工隧洞设计提供一种有效的分析方法。

高压引水隧洞；弹性荷载；接触力法；衬砌开裂；渗透系数；渗透荷载

随着我国经济建设的蓬勃发展，出现了越来越多的高水头电站、深部地下工程，在这些工程中存在着大量的长大引水隧洞，其突出特点是埋深大、水压高、地质条件复杂，给工程建设带来了极大的挑战[1]。在高水头作用下特别是岩体条件较差时，引水隧洞一般采用钢衬钢筋混凝土结构，形成了钢衬、衬砌和围岩相互作用的复杂结构体。引水隧洞在高内水压力作用下，钢衬会发生变形，逐渐与衬砌结构接触，形成钢衬、衬砌与围岩相互接触联合承载的复杂状态，当内水压力逐渐增大时，衬砌会进入损伤演化过程并最终出现宏观裂缝，内水沿着开裂的缝隙渗入周围岩体，产生内水外渗现象[2]。其运行期全过程可以分为以下3个阶段：1) 钢衬单独承载，缝隙闭合阶段；2) 衬砌未开裂，衬砌与围岩复杂接触联合承载阶段；3) 衬砌开裂，内水外渗阶段。长期以来，许多中外学者对水工隧洞运行期全过程力学问题进行了深入的探讨，在理论和试验研究方面取得了大量的成果。在钢衬单独承载方面，主要采用解析法[3]求得弹性荷载系数，但对于荷载不均匀情况以及非圆形隧洞适应性较差。在复杂接触状态模拟方面，目前的数值计算方法主要有拉格朗日乘子法、罚函数方法、线性补偿法以及接触单元法[4]，但这些方法往往会增加系统的自由度，且需迭代计算，在接触单元较多、接触状态复杂的结构受力求解中计算精度和稳定性较差。在衬砌开裂模拟方面，主要通过解析法[5−6]以及对衬砌开裂后的渗流场[7−8]进行求解得到渗透附加荷载，或通过压水试验研究渗流作用对岩体应力和变形的影响[9−10]，但对于衬砌渗透系数和渗透荷载的计算方法以及衬砌开裂对围岩稳定影响方面存在一定不足。本文作者在以上研究的基础上，采用三维弹塑性损伤有限元对引水隧洞运行期全过程进行模拟，分别提出钢衬单独承载弹性荷载求解方法、基于非线性弹性本构的接触力法以及考虑应力和损伤影响后的渗透系数和渗透荷载计算方法，以便为岩体工程地下水工隧洞设计提供一种有效的分析方法。

1 钢衬单独承载阶段

当引水隧洞直径和水头很大，或赋存岩体条件较差时，一般采用钢衬钢筋混凝土结构。同时为了使钢衬承担尽可能多的内水荷载，常在钢衬与衬砌之间预留缝隙，钢衬在与衬砌接触之前，存在一个单独承载变形的阶段。

假设钢衬与衬砌结构之间的初始缝隙值为，且沿洞周均匀分布，则隧洞在内水压力作用下，一部分荷载使钢衬单独受力而向外变形，填满初始缝隙，剩余荷载则由钢衬、衬砌以及围岩联合承担。其弹性荷载求解步骤如下。

1) 采用三维弹性有限元计算在内水荷载作用下，钢衬单独承载时的变形量为

2) 求得钢衬外圈节点的径向位移U为

(2)

式中：为钢衬外圈节点的单位法向矢量。

(4)

2 衬砌未开裂复杂接触阶段

对于钢衬单独承担的荷载1可一次施加进行有限元计算，而对于剩余荷载2，由于存在复杂受力过程和接触状态，需进行分级迭代计算：

为了保证迭代计算的平衡，在前几级计算中把荷载加大，而在后几级中把荷载减小，即加权分配各级荷载。若将荷载2分级，则分级总权数1+2…，第级的荷载则为

(7)

本文针对衬砌与围岩之间的接触问题，提出一种考虑接触面黏结滑移特性的接触力算法[11]。

加载前，衬砌与围岩接触面上节点呈点对黏结接触状态，加载后，接触点对间会出现黏结接触、滑动接触和分离3种状态，需根据接触面的受力和变形条件进行判别。

若第−1级荷载迭代计算完成后，接触点对的总位移分别为和，第级荷载作用时在不考虑接触力的情况下，可得到接触点对的总位移和，由此可以得到不考虑接触力作用的接触点对的相对法向位移和切向位移：

(9)

式中：为接触面在接触节点处的单位法向矢量。

接触面在复杂外荷载的作用下其应力−应变关系常表现出一定的非线性，同时，在发生剪切变形和受高压应力作用时，可能产生沿粗糙体表面的滑移、剪断、压碎和磨损、拉裂等现象，针对接触面的非线性特性，采用非线性双曲线本构模型[12−13]描述接触面法向和切向刚度变化规律：

(11)

式中：K为接触面初始法向刚度；d为接触点对的法向相对位移；dmax为接触点对允许法向最大相对位移；为混凝土材料的泊松比。其中：K和dmax与节理面张开度、强度和粗糙程度有关，可通过经验公式[14]求得。

式中：K和K分别为第级荷载作用完成后接触面的法向和切向刚度；和分别为法向和切向力，，。

根据求得的接触点对附加荷载按照下式对第级荷载结构受力情况进行修正：

(15)

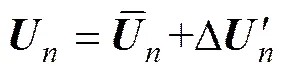
3 衬砌开裂内水外渗阶段

衬砌开裂前，衬砌混凝土可视为均质材料，其渗透性很低，衬砌承担了较大的内水压力。随着承受的水头越来越高，在内水压力作用下衬砌容易产生拉裂，导致内水外渗。一般地，当混凝土衬砌单元的最大主应变＞(混凝土的极限拉应变)时，则认为混凝土衬砌开裂。

对于混凝土衬砌可采用MAZARS根据混凝土拉伸试验拟合的各向同性弹性损伤模型[15]：

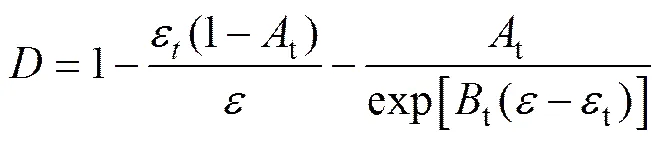
式中：t和t为试验曲线拟合常数，对于一般混凝土0.7＜t＜1，104＜t＜105；为混凝土极限拉伸应变；为衬砌单元的第1主应变。

混凝土衬砌开裂前，可视为各向同性线弹性材料，衬砌开裂后，假设衬砌裂缝的发展方向垂直于单元最大主应变方向，因此，沿最大主应变方向的刚度会逐渐降低，混凝土开裂单元的应力和应变关系需根据单元的损伤开裂程度按各向异性材料进行修正，得到局部坐标系下的应力矩阵[16]为

混凝土和岩石均属于脆性材料，其力学特性、损伤破坏机制较相近。基于杨天鸿等[17]对不同岩性的岩石进行的应力−应变全过程渗透试验以及LOUIS[18]通过钻孔加压实验提出的渗透系数与正应力的经验公式，考虑损伤演化对渗流场的影响，引入渗透突跳系数来描述混凝土应力和损伤对渗流的影响机制。对于不同的应力和损伤发展阶段，的取值也发生相应改变[19]，以反映在损伤破裂过程中渗透性突变的规律，表1所示为不同单元状态下的渗透突跳系数。一般地，当损伤系数＜0.98时，认为衬砌混凝土处于损伤开裂阶段，当损伤系数≥0.98时，则认为衬砌混凝土处于损伤断裂阶段。考虑应力和损伤影响后的主应力方向渗透系数的表达式为

式中：0为材料初始渗透系数；为试验确定的耦合系数；为单元的有效应力。

表1 不同单元状态下的渗透突跳系数

对于各向异性均匀介质，根据达西渗透定律，可以导出稳定渗流场的微分方程：

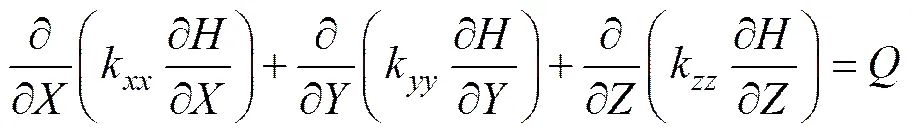
式中：带下标的为计算坐标下的渗透系数；为内源；为水头。对上式进行积分求和，可得出三维有限元渗流的基本方程：

(21)

式中：{}为单元结点水头；{}为对渗流边界进行积分得到的结点荷载；[]为三维渗流有限元的单元传导矩阵。从而得到衬砌开裂后渗透荷载：

则衬砌开裂后第级荷载结构受力按照下式修正：

(23)

4 工程实例

4.1 工程概况和计算条件

某水电站引水隧洞全长7 126 m，沿线地面波状起伏，经过不同的地质构造区，本文选取0+000.00—0+180.00段进行分析，其中跨越18 m长的凝灰岩夹层带。该隧洞段位于引水系统尾部，采用圆形断面结构，开挖洞径为10.2 m，衬砌后过水洞径为9.0 m，洞室中心高程为32.00 m，洞室埋深为143.67 m，最大内水水头为135.24 m，采用钢筋混凝土结构，其中衬砌厚度约为0.6 m，采用C25混凝土。凝灰岩夹层穿过部位，围岩条件较差，局部采用钢衬支护，钢衬厚度为24 mm，弹性模量为210 GPa，钢衬与混凝土预留缝隙为1.5 mm。

引水隧洞三维有限元模型采用八节点六面体单元，共剖分了43 736个等参单元，其中开挖单元5 264个，钢衬单元144个，混凝土衬砌单元2 016个。模型范围及坐标系如下：方向从−90.0 m到90.0 m，与洞轴线垂直；方向从0 m到180.0 m，与洞轴线重合，顺水流为正；向从−48.0 m到175.67 m，与大地坐标系平行。引水隧洞三维有限元模型如图1所示，衬砌与钢衬支护模型如图2所示。

初始地应力场通过实测地应力反演获得，隧洞区域第1主应力在−5~−7 MPa范围内，属于偏低地应力场。引水隧洞区域岩体以Ⅲ类为主，凝灰岩夹层带为Ⅳ类，材料力学参数见表2。

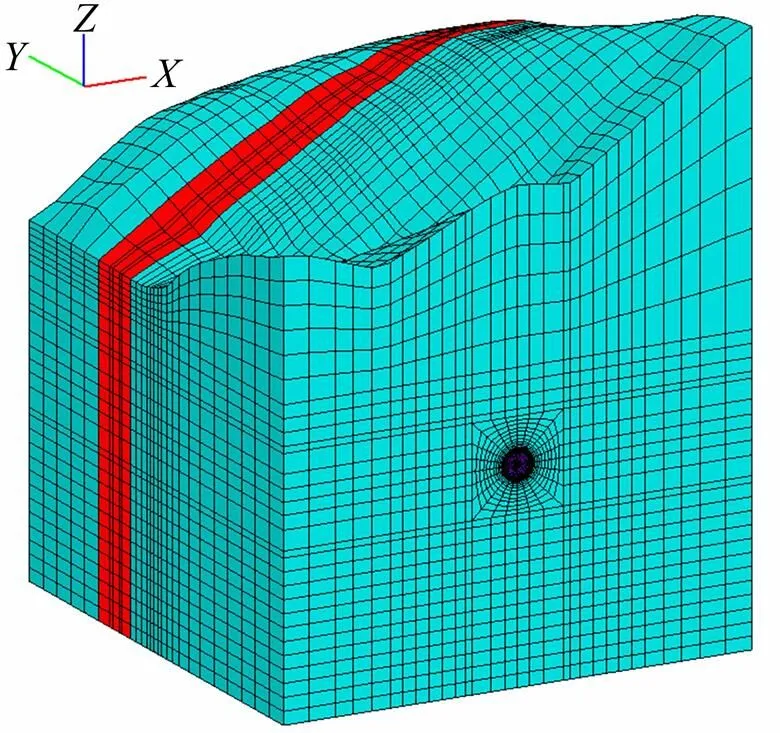
图1 引水隧洞三维有限元模型

(a) 混凝土衬砌；(b) 局部钢衬

采用三维弹塑性损伤有限元对引水隧洞运行期全过程进行数值模拟，以凝灰岩夹层穿过段为典型断面，对引水隧洞运行期复杂承载过程进行分析。

4.2 计算结果分析

4.2.1 钢衬单独承载弹性荷载系数

采用弹性有限元模拟钢衬初始缝隙闭合过程，得到钢衬各作用点所承担内水压力的比例系数，如图3所示。

由计算结果可以看出，钢衬所承担弹性荷载的比例系数在0.20~0.32范围内，由于受混凝土、钢衬自重以及内水压力荷载梯度分布的影响，从上到下逐渐减小，但钢衬各作用点所承担的水头值基本相同，约37 m，与解析解基本一致。

4.2.2 衬砌损伤系数与接触面破坏模式

采用三维弹塑性损伤有限元模拟钢衬初始缝隙闭合后，衬砌与围岩的联合承载过程。衬砌开裂前，混凝土衬砌承担大部分的内水压力，接触面受力状态良好，基本处于黏结接触状态。衬砌开裂后，内水外渗，部分内水压力直接由围岩承担，接触面出现一定范围的分离、滑移区。衬砌结构损伤系数如图4所示，接触面破坏模式如图5所示。

图3 钢衬单独承载系数

由图4可以看出：随着内水压力的逐渐增加，衬砌破坏区逐渐由腰拱向顶部和底部扩展，当内水压力达到135 m时，衬砌结构最大主应力基本均超过混凝土的抗拉强度，进入开裂阶段，其中，腰拱部位损伤程度最大，进入损伤断裂阶段，并逐渐向腰拱两端扩展。

由图5可以看出：随着混凝土衬砌开裂破坏程度的加剧，产生内水外渗，围岩承担较大的内水水头，并作用于衬砌与围岩接触面，造成局部开裂、滑移。由于腰拱部位衬砌开裂破坏严重，外渗水头较大，造成腰拱部位接触面拉裂破坏，并逐渐向两侧延伸。

图4 衬砌结构损伤系数

表2 材料力学参数

图5 接触面破坏模式

4.2.3 衬砌开裂渗流场分布与对围岩稳定影响

通过三维渗流场分析，得到衬砌开裂后渗流场分布结果如图6所示。由图6可以看出：当内水压力达到100 m时，衬砌单元最大主应变基本超过混凝土极限拉应变进入损伤状态，由于腰拱以及拱底衬砌损伤严重，混凝土渗透系数有较大提升，使得该部位水力梯度减小，压力水头等值线分布稀疏，而其余部位渗流压力水头等值线分布密集。

图6 衬砌开裂后压力水头等值线分布

为了体现衬砌开裂后内水外渗对引水隧洞围岩稳定的影响，将渗流场计算得到的渗透荷载作用于围岩，得到考虑内水外渗后洞周围岩破坏区分布结果如图7所示，并与不考虑渗透荷载作用时洞周围岩破坏情况进行对比分析。图8所示为不考虑内水外渗围岩破 坏区。

图7 考虑内水外渗围岩破坏区

图8 不考虑内水外渗围岩破坏区

从计算结果可以看出：考虑衬砌开裂后内水外渗情况时，围岩承担的内水压力增大，洞周围岩破坏区有所增加，在衬砌开裂严重、外渗水头较大的腰拱部位破坏区增加较大，并逐渐向两侧延伸。这说明不考虑内水外渗情况对于隧洞洞周围岩破坏区计算偏于保守，采用衬砌损伤开裂内水外渗计算模型对于工程分析具有积极的意义。

5 结论

1) 钢衬所承担弹性荷载的比例系数在0.20~0.32范围内，各作用点所承担的水头约37 m。说明采用有初始缝隙的钢衬结构对减少衬砌和围岩承载具有较大的作用。

2) 在高内水压力作用下，衬砌结构基本进入开裂阶段，腰拱部位损伤程度最大，进入损伤断裂阶段，并逐渐向腰拱两端扩展，且在腰拱衬砌开裂严重部位局部出现接触面拉裂破坏。

3) 在外渗水头荷载作用下，围岩的塑性破坏区有一定程度增加，在腰拱衬砌开裂破坏严重部位塑性区增加明显，说明内水外渗对围岩稳定具有一定影响。

[1] 张有天. 岩石水力学与工程[M]. 北京: 中国水利水电出版社, 2005: 31−32. ZHANG Youtian. Rock hydraulics and engineering[M]. Beijing: China Water Power Press, 2005: 31−32.

[2] 赵延林, 曹平, 汪易显, 等. 裂隙岩体渗流–损伤–断裂耦合模型及其应用[J]. 岩石力学与工程学报, 2008, 27(8): 1634−1643. ZHAO Yanlin, CAO Ping, WANG Yixian, et al. Coupling model of seepage-damage-fracture in fractured rock masses and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1634−1643.

[3] SCHLEISS A J. Design of reinforced concrete linings of pressure tunnels and shafts[J]. Hydropower & Dams, 1997, 4(3): 88−94.

[4] 张楚汉. 论岩石、混凝土离散−接触−断裂分析[J]. 岩石力学与工程学报, 2008, 27(2): 217−220.ZHANG Chuhan. Discrete-contact-fracture analysis of rock and concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 217−220.

[5] 王明斌, 李术才. 含衬砌圆形压力隧洞弹塑性新解[J]. 岩石力学与工程学报, 2007, 26(增2): 3770−3775. WANG Mingbin, LI Shucai. New elastoplastic solutions to circular pressured tunnel with lining[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp 2): 3770−3775.

[6] 张常光, 张庆贺, 赵均海, 等. 具有衬砌的圆形水工隧洞弹塑性应力统一解[J]. 同济大学学报(自然科学版), 2010, 38(1): 51−53. ZHANG Changguang, ZHANG Qinghe, ZHAO Junhai, et al. Elastic-plastic stress unified solutions of a circular hydraulic with lining[J]. Journal of Tongji University (Natural Science), 2010, 38(1): 51−53.

[7] 卞康, 肖明. 水工隧洞衬砌水压致裂过程的渗流−损伤−应力耦合分析[J]. 岩石力学与工程学报, 2010, 29(增2): 3770−3774. BIAN Kang, XIAO Ming. Seepage-damage-stress coupling analysis of hydraulic tunnel lining in hydraulic fracturing process[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Suppl 2): 3770−3774.

[8] 苏凯, 伍鹤皋. 水工隧洞内水外渗耦合分析[J]. 岩土力学, 2009, 30(4): 1147−1151. SU Kai, WU Hegao. Analysis of hydro-mechanical interaction in hydraulic tunnel with inner water exosmosis[J]. Rock and Soil Mechanics, 2009, 30(4): 1147−1151.

[9] 蒋中明, 冯树荣, 傅胜, 等. 某水工隧洞裂隙岩体高水头作用下的渗透性试验研究[J]. 岩土力学, 2010, 31(3): 673−676. JIANG Zhongming, FENG Shurong, FU Sheng, et al. Test study of osmotic behavior of fractured rock mass of water tunnel under high water pressure[J]. Rock and Soil Mechanics, 2010, 31(3): 673−676.

[10] 卞康, 肖明. 高压水工隧洞钢筋混凝土衬砌开裂渗漏研究[J]. 岩石力学与工程学报, 2010, 29(增2): 3648−3654. BIAN Kang, XIAO Ming. Research on seepage of high pressure hydraulic tunnel when reinforced concrete lining cracking[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Suppl 2): 3648−3654.

[11] LIU J B, SHAILENDRA K. Analysis of dynamic contact of cracks in viscoelastic media[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 121(1/2/3/4): 187−200.

[12] BARTON N, BANDIS S, BAKBTAR K. Strength, deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1985, 22(3): 121−140.

[13] KULHAWY F H. Stress deformation properties of rock and rock discontinuities[J]. Engineering Geology, 1975, 9(4): 327−350.

[14] BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock fracture deformation[J]. International Journal of Rock Mechanics and Mining Sciences and Geo-mechanics Abstracts, 1983, 20(6): 249−268.

[15] 余天庆, 钱济成. 损伤理论及应用[M]. 北京: 国防工业出版社, 1993: 141−146. YU Tianqing, QIAN Jicheng. Damage theory and its application[M]. Beijing: National Defence Industry Press, 1993: 141−146.

[16] 苏凯, 伍鹤皋. 水工隧洞钢筋混凝土衬砌非线性有限元分析[J]. 岩土力学, 2005, 26(9): 1485−1490. SU Kai, WU Hegao. Nonlinear finite element analysis of reinforced concrete lining of hydraulic tunnels[J]. Rock and Soil Mechanics, 2005, 26(9): 1485−1490.

[17] 杨天鸿, 唐春安, 李连崇, 等. 非均匀岩石破裂过程渗透率演化规律研究[J]. 岩石力学与工程学报, 2004, 23(5): 758−762. YANG Tianhong, TANG Chunan, LI Lianchong, et al. Study of permeability evolution in failure process of inhomogeneous rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 758−762.

[18] LOUIS C. Rock hydraulics in rock mechanics[M]. MULLER L, ed. New York: Verlay Wien, 1974: 287−299.

[19] 杨天鸿, 唐春安, 芮勇勤, 等. 不同围压作用下非均匀岩石水压致裂过程的数值模拟[J]. 计算力学学报, 2004, 21(4): 419−424. YANG Tianhong, TANG Chunan, RUI Yongqing, et al. Numerical simulation of hydraulic fracturing process in heterogeneous rocks under different confining pressures[J]. Chinese Journal of Computational Mechanics, 2004, 21(4): 419−424.

(编辑 陈爱华)

Numerical analysis for complex bearing process of high pressure diversion tunnel at runtime

DENG Jian1, 2, XIAO Ming1, 2, CHEN Juntao1, 2

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China)

In light of the working mechanism of the diversion tunnel at runtime, the whole process of runtime was divided into three stages: the initial gap closure stage with steel lining bearing separately, the complex contact and combined bearing stage of lining and surrounding rocks without lining cracks, inner water exosmosis stage with lining cracks. According to the mechanical properties in every stage, three kinds of method, i.e., a solution method of elastic load when the steel lining works alone, an analysis method of combined bearing of lining and surrounding rocks based on contact force method, and a calculation method of permeability coefficient and seepage load considering the effect of stress and damage were put forward. From all the above, a finite element calculation program was compiled. Taking some diversion tunnels as engineering example, the whole process of runtime was simulated. The project example calculation results can reasonably reflect the mechanical characteristic of diversion tunnel under high inner water pressure during the whole process of runtime, and an effective analysis method is provided for the design of hydraulic tunnel.

high pressure diversion tunnel; elastic load; contact force method; lining cracking; permeability coefficient; seepage load

10.11817/j.issn.1672-7207.2017.05.019

TU45

A

1672−7207(2017)05−1261−07

2016−07−08；

2016−09−27

国家重点基础研究发展规划(973计划)项目(2015CB057904)；国家自然科学基金资助项目(91215301，51279136) (Project(2015CB057904) supported by Major State Basic Research Development Program (973 Program) of China; Projects(91215301, 51279136) supported by the National Natural Science Foundation of China)

肖明，博士，教授，从事地下结构稳定数值分析方面研究；E-mail: mxiao@whu.edu.cn