竖井正方形地基固结度解答及其应用

牛犇，唐晓武，张超杰，陈秀良



竖井正方形地基固结度解答及其应用

牛犇1, 3, 4，唐晓武2，张超杰5，陈秀良5

(1. 中交四航工程研究院有限公司，广东广州，510230；2. 浙江大学滨海与城市岩土工程研究中心，浙江杭州，310058；3. 中交交通基础工程环保与安全重点实验室，广东广州，510230；4. 华南理工大学土木与交通学院，广东广州，510641；5. 浙江省水利河口研究院，浙江杭州，310020)

推导考虑正方形影响区以及影响区边界透水性的竖井地基固结度解答式。在面积相同的情况下，不同形状的影响区(正方形、正六边形、圆形)的固结度计算结果存在一定的差别。用圆形形状代替正六边形形状产生较小的计算误差，而用圆形形状代替正方形形状则会产生较大的计算误差。在考虑时间离散以及孔压传递的因素的基础上，将竖井正方形固结解应用于对模袋系统固结度的估算，估算结果与有限元计算结果基本完全吻合，而与实际室内实验结果存在较小误差，但是在误差允许范围之内。通过几何参数分析，为设计人员改善系统排水条件、实现加快系统固结提供参考，通过物性参数分析，对模袋系统材料的选取提供依据。

正方形影响区；边界透水；排水板；模袋；固结

经典理论对于砂井地基固结问题的求解是对砂井周围影响区域进行假设，将其等效简化为圆形区域进行推导计算[1−5]。实际上，在真实施工条件[6−9]下，排水板的打设存在一机多带同步施工，两排或者三排排水板同时打设，最终形成的砂井影响区域是正方形或者是正六边形[10−11]，而简化为圆形区域则将与实际情况存在一定偏差。在圆形区域形状的固结理论中，对于同一深度的截面，最终的固结度与影响区域的半径e成相关变化，同一半径的圆上的点其固结度都是相同的。而将影响区考虑为更加接近实际的正方形时，其固结性状及其影响因素有待研究。基于以上分析，本文考虑砂井周围影响区域为正方形形状，推导正方形影响区情况下砂井地基固结问题的固结度解答。在考虑时间离散和孔压传递的因素之后，将理论解答应用于打设排水板充泥模袋固结问题的估算。最后，对竖井正方形地基固结解在模袋系统中的应用理论进行几何参数和物性参数分析，得到固结度受参数变化的影响规律及对相关参数的敏感性。

1 理论推导

本文参考了六边形形状影响区的砂井地基理 论[10−11]以及部分透水边界问题[12−14]的研究，对考虑正方形形状影响区和部分透水边界的固结问题进行了建模及公式推导。

1.1 假设条件

在推导正方形影响区、部分透水边界、有涂抹区、两面透水的固结理论过程中，影响区、涂抹区、砂井形状均等效为正方形。其假设条件如下。

1) 考虑Barron的等应变条件。沿向的固结考虑沿横截面的平均超孔隙水压力。

向为图1中垂直于平面的方向。

2) 为模型简化计算，假设顶部的荷载为一次瞬时施加并保持恒定，并有以下条件成立：

3) 求解过程中连续条件为：排水板与土体交界面孔压和流量连续。

1.2 正方形影响区求解

正方形影响区的固结度解析解求解模型如图1所示。由于正方形呈对称形状，故只需对其中1/8部分进行求解。图1中：和为正方形影响区的半径；和为排水板半径；和为涂抹区半径；w为排水板的渗透系数；x为土体的渗透系数；s为涂抹区的渗透系数；01为部分透水边界的渗透系数；和分别为部分透水层在和方向的厚度。以下解答均基于如图1所示的1/4正方形区域的上部三角形区域进行求解。

图1中用斜线标注的阴影区域为研究的对象。横截面为阴影区域、厚度为d的土体单元在d时间内流出的水量为

k为沿土体方向的渗透系数；为阴影单元的面积，大小为。

图1 模型截面计算简图

土体单元体积变化为

由d=d，土体单元流量变化等于阴影单元体体积变化，得到土体单元控制方程为

(3)

由假设(3)和(1)，并考虑两端透水的边界条件得：

(5)

；；；(6)

其中：为砂井地基总深度。

根据控制方程，并依据假设条件(4)，(5)和(6)，得到图1中模型的平均孔压及固结度最终解答为：

(8)

其中：

；；；

；；；

；

1.3 正方形、正六边形、圆形影响区解答的比较

在得到以上正方形影响区固结解后，将该解与正六边形形状影响区的解[10]以及工程实际中广泛采用的谢康和单井圆形影响区固结解[15−16]进行对比。选择圆形半径为，利用面积等效得到了正方形影响区、正六边形影响区的几何参数。三者几何尺寸示意图如图2所示，不同形状固结解结果对比如图3所示。

由图3可见：不同影响区形状固结度解答所得到的固结规律是一致的，3条固结曲线形状类似；正六边形影响区与经典圆形影响区相比，其固结度计算结果十分相近，最大处不超过4%；但是正方形影响区与圆形影响区相比，则存在较大的误差；在正方形影响区固结度达到50%时，其最大固结度差值达9%，此时相对误差达18%。另外，横坐标轴是以时间因子取对数之后标识的，以达到相同固结度来对比正方形影响区与圆形影响区对应的时间，计算结果表明：用圆形形状影响区来替代正六边形影响区计算土体固结是合适的，其结果在工程允许范围之内，而用圆形形状影响区代替正方形影响区计算土体固结度则存在较大误差，此时就有必要考虑实际的正方形影响区形状对固结问题进行计算。

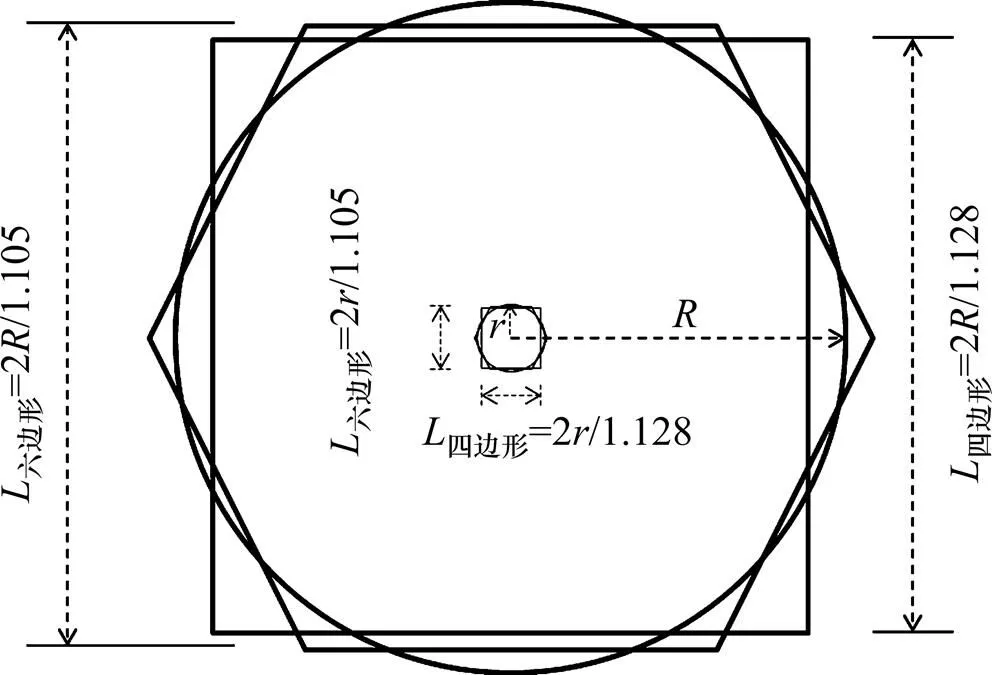
图2 面积相等的正方形、正六边形和圆形区域

1—四边形影响区；2—六边形影响区；3—圆形影响区。

2 在模袋固结问题中的应用

近年来，沿海地区加大对滩涂资源的利用，围垦项目增多[17−19]。在海堤填筑中，出现了新的采用充泥模袋的施工工艺(如慈溪四灶浦围涂工程的冲泥模袋)。相对于传统工艺[20−24]而言，应用充泥模袋作为海堤的主体结构优点较多，能够解决石料需求量大、造价昂贵、施工工期长、断面尺寸大等各种问题。

新型充泥模袋的施工过程为：将滩涂淤泥填充进土工模袋(其中包含埋设排水板的过程)，待其固结至满足设计要求，作为填充材料填筑海堤堤心。在此施工工艺中，充泥模袋系统的固结速率是影响施工的工期最关键的因素。在模袋内部打设排水板，增加了排水通道，加快模袋系统固结速率，缩短施工工期。

将淤泥填充进模袋，根据不同的模袋材质，模袋的横向截面形状存在2种情况：材质软的模袋变为上部为半个椭圆下部为近似半个长方形的整体形状，材质硬或者边角处有骨架的土工管袋则变为近似的正方形形状。无论是哪一种形状，随着固结的进行，模袋都会逐渐变得扁平，最终固结完成时，模袋截面变成1个扁平的长方形形状。软质材料模袋的变形示意图如图4所示。

图4 软质模袋变形示意图

2.1 长方形截面固结度表达式

根据描述，打设排水板充泥模袋体系的固结问题可以考虑为水平放置、周边为部分透水边界的砂井地基固结问题，可应用本文得出的考虑边界透水性的竖井正方形地基固结度解答来估算其固结结果。相比于考虑采用圆形影响区的解答来估算，应用正方形形状的解答更准确。

如果考虑模袋系统固结所形成的截面为正方形，可以将本文推导的固结解直接应用于计算。但是，一般来说，随着泥的固结，模袋外形会形成1个扁平的长方形，所以，为其分配权重系数，应用竖井正方形地基固结解对长方形形状的解答进行估算。

具体思路为：分别求出以长方形截面的长、宽为边长的正方形截面的固结度解答，为其分配权重系数。长方形截面形状固结度估算结果表达为

在此基础上，为考虑充泥模袋体系的固结过程，将固结时间进行离散，充分考虑固结过程中的各个参数变化。

将模袋系统的固结过程分为数个阶段，每个阶段均采用式(9)的估算表达式进行计算。同时，在每个阶段的初始时，考虑了初始超静孔压的传递：

(11)

2.2 充泥模袋系统固结度估算结果的验证

本节利用2.1节中的方法进行计算，同时，将结果与有限元软件ABAQUS模拟结果及实际室内实验结果进行比较。计算参数均来源于浙江省水利河口研究院的浙江省科技厅院所重大专项“滨海淤泥资源化利用关键技术研究创新人才培养”科研项目实验。

2.2.1 理论算例参数与有限元计算

在计算中，式(9)中的参数分恒定不变与逐步变化2种情况。

实验分5级加载，每级荷载施加时间为5 d，计算同样划分为5个阶段。计算过程中恒定不变的参数取值见表1。变化的参数包括每个阶段模袋两端的荷载、模袋土的渗透系数、模袋土的压缩模量、初始孔压，见表2。其中初始孔压的计算方法参见式(10)。第1阶段的初始平均超静孔压为0，其后每个阶段的初始平均孔压则根据计算得出。表2中，和分别表示大、小正方形的初始平均超静孔压计算结果。

同时，同步利用ABAQUS进行有限元分析计算。土体本构采用摩尔库仑模型。模袋体系的模型实体图及框架图见图5(a)。计算分析步设置2步：第1步为施加荷载阶段，时间取尽量短，0.001 s；第2阶段为土体固结阶段，采用自动步长。起始步长为2×105s。见图5(b)。

约束条件设置：限制底面沿竖向(向)位移；限制沿方向模型两表面的变形；在固结阶段刚开始时，模型所有表面孔压为0。

模型网格划分如图5(c)所示。

计算结果数据提取：应用数理统计的原理，在为−0.35，−0.20，0，0.20和0.35这5个截面取数据点(沿轴方向的区间范围为(−0.405，0.405))，然后，将所有数据点的固结度计算结果取平均值，即认为是整体模型固结度的平均值。

2.2.2 室内实验

室内实验于浙江省水利河口研究院六堡试验基地进行。

模袋淤泥土取自平阳宋埠—西湾围海造地工程现场，土样的天然含水量质量分数为65%，土颗粒相对密度为2.687，黏粒和胶粒质量分数为47.6%，为高液限黏土，基本土工物理指标见表 3。

(a) 模袋体系三维实体及框架图；(b) 分析计算步；(c) 模袋体系网格划分

实验采用分5级加载。模袋内部淤泥采用泥浆泵泵入，排水板在泥浆高度达到模袋高度的一半时进行埋设。打入淤泥的平均含水量119.6%，模袋上通过平板施加均布外力排水。在模袋内部中心及底部位置埋设孔压计，测量孔隙水压力。

2.2.3 结果对比

通过进行估算方法计算、有限元计算以及实际的室内实验，理论计算结果、数模计算结果及室内实验结果见图6。

从图6可见：大正方形固结度计算结果靠近实际的室内实验结果，而小正方形的固结度计算结果与室内实验结果相比则偏差较大。

在模袋土的固结过程中，固结中形成1个扁平的长方形截面，在此，仅考虑模袋土横截面的排水情况。由于上下两面的排水距离要比左右两边的排水距离短的多，因此，大部分水选择从上下两面排出，而少部分的土体中的水主要是左右两边靠近模袋的土体中的水，选择从左右两界面排出。从排水时间上来说，从长边排出的这部分水其排出时间应该接近于直接从大正方形形状截面排出的时间；而少量的、从短边排出的水其排出时间接近于直接从相应小正方形形状截面排出的时间，而且由于水量少，这部分水的排出时间会小于从长边排出的大量水的排出时间，这就导致整个模袋土中水的排出速度稍微比同样多的水仅从大正方形排出的速度要快一些。另外，小正方形截面固结的时间要远远小于大正方形截面的固结时间，因为往周边的排水距离要小得多。结合这2点，模袋土的固结所需的时间应该接近于并稍微小于长边形成的大正方形的固结时间，而远远大于小正方形固结所需的时间。图6中，实际室内实验的结果曲线与大、小正方形的固结结果曲线之间的关系很好地印证了这一点。

表1 时间离散方法计算中恒定不变的参数

表2 时间离散方法计算中发生变化的参数

表3 平阳软土基本土工物理指标

图6 时间离散方法、有限元与实验结果的对比

其次，比较由公式得到的长方形与大小正方形固结度计算结果。由于设置了权重，长方形形状的固结曲线介于大小正方形固结度曲线之间。由于排水距离短，大量水需从长方形形状的长边排出。对于这种工况，需对大小正方形计算得到的固结度结果设置相应权重系数。式(9)中的和代表的不是边长，它们代表了从长边、短边排出水的水量，权重系数和是通过从长短边排出水占总水量的比例而设置的。最终长方形固结度公式表达式的计算结果与实际室内实验的结果相吻合，这在图6中得到了验证。

最后，本文应用有限元进行了计算。计算结果表明，有限元的计算结果与本文提出的估算方法的计算结果基本上吻合。与实际室内实验结果相比，两者存在差别。其中第2和第3阶段稍有差别，其他阶段差别非常小，应该说在误差允许范围内。实际的结果印证了固结度的变化规律。

3 竖井正方形地基固结解应用的参数分析

在实际应用中，找出影响固结速率的关键参数，在满足设计要求的前提下，提高固结速率至关重要，因为它直接影响到项目工期、项目成本等。以下通过绘制各关键参数单独变化时的固结度变化曲线，分析各因素对最终固结度的影响程度。

具体研究采用如下方法：采用表1和表2中参数计算的算例作为标准算例；之后，在每一组参数分析算例的计算过程中，对唯一的目的参数在标准算例参数的基础上进行改变，其余参数均保持不变。

3.1 几何参数分析

首先针对几何参数开展研究。

模袋厚度的敏感性计算和土体宽度的敏感性计算结果见图7和图8。

由图7可见：在其余条件相同时，模袋的厚度越小，模袋系统的固结速度越快。厚度为0.005 m与厚度为0.010 m之间的固结速率提升，与厚度为0.010 m和0.020 m的结果相比，提升较小。可初步判断：随厚度减小，固结速率的提升空间可能会变小。考虑到模袋的强度性能，因此，可通过开展试验，在满足力学要求的前提下，赋予模袋厚度1个性价比较高的设计值。

b′/m：1—0.020；2—0.010；3—0.005。

1—2a=0.667 m, 2b=0.333 m, 2a/2b=2；2—2a=0.800 m, 2b=0.200 m, 2a/2b=4；3—2a=0.875 m, 2b=0.125 m, 2a/2b=7。

由图8可见：在截面周长一定的前提下，模袋系统的宽高比越大，系统固结越快。同样，模袋系统的宽高比也存在1个合适值；随着宽高比的增加，固结速度的提升程度(曲线差值)逐渐减小。这表明宽高比增加，固结速度的提升同样存在1个极限。结合理论计算以及有限元的计算结果，取宽高比为4既保证了固结速度，又不会浪费模袋制作材料。宽高比值4推荐作为模袋的设计值。

3.2 物性参数分析

模袋体系的物性参数分析中，关键参数有2个：模袋的渗透系数和土体的压缩模量。敏感性计算结果见图9和图10。

k01/(m∙s−1)：1—1×10−7；2—1×10−8；3—1×10−9。

由图9可见：在初始渗透系数较小时，固结度受模袋渗透系数改变的影响较大；当渗透系数提升1个数量级(由1×10−9 m/s提高到1×10−8 m/s)时，固结速度约提升25%；但当模袋的渗透系数继续由1×10−8 m/s提高到1×10−7 m/s时，固结速度提升不大。事实上，模袋系统中的水排出经过了土体与模袋两道屏障，在水到达土体边缘接近模袋时，若在模袋上基本能够自由排出，则此时系统的排水速度主要取决于水经过土体的速度，也即取决于土体的渗透系数。此时，仅单独提升模袋的渗透系数，系统的固结速度提升无明显效果。

实际中，系统的固结速率主要受模袋土渗透系数的影响。实际中水从模袋土(淤泥)中的排出速度非常小，同时模袋的渗透系数比淤泥土的渗透系数大得多，水的排出时间主要耗费在淤泥中，因此，整个系统的固结效率主要与淤泥土的渗透系数有关。

图10中，1.5倍或者0.5倍原土体压缩系数是指将标准算例中不同阶段的土体压缩模量同时乘以1个相同(1.5或者0.5)的比例系数。土体压缩模量对于固结度的影响程度比较明显，土体压缩模量越大，系统固结越快。但同时，固结度也存在提升的性价比问题。

结合图7~10的结果分析，在模袋系统的固结度效率提升上，考虑单因素时，几何参数和物性参数都有一定的极限值，并不是一味地增大或者减小某个参数，便可有效地提升固结速度。可通过试验结合理论分析，确定某一个因素的合理取值，或通过参数的组合变化，确定具有较高性价比的参数组合。系统固结速度的提升受多种因素的制约，合适的参数取值将为实际项目提升质量、提高效率、降低成本提供支撑。

1—1.5倍原土体压缩模量；2—原土体压缩模量；3—0.5倍原土体压缩模量。

3.3 参数分析

几何参数的分析可以为设计人员改善系统的排水条件、加快固结速度、缩短固结周期提供理论依据。系统无论对于几何参数的选择还是物性参数的变化，均存在一定的约束。参数敏感性见表4。

表4 固结度对参数的敏感性

4 结论

1) 推导了考虑影响区形状为更接近实际的正方形区域以及考虑边界透水性的竖井地基固结理论。本文与正六边形影响区以及圆形影响区固结度计算结果的对比表明，用圆形影响区代替正六边形影响区计算误差较小，满足工程需要；而用圆形影响区代替正方形影响区的计算存在较大误差。

2) 将竖井正方形固结解应用于实际打设排水板充泥模袋体系的固结度计算。通过将时间进行离散，依据排水量设置权重系数，利用正方形形状影响区的固结度解答对于长方形截面的模袋体系的固结问题进行了估算，估算结果与有限元计算结果基本完全吻合，与实际实验结果相比存在较小误差，但是在误差允许范围之内。

3) 通过几何参数分析，为设计人员改善系统排水条件、实现加快系统固结提供参考；通过物性参数分析，为模袋系统材料的选取提供定性依据。

[1] WALKER R, INDRARATNA B. Vertical drain consolidation wigh parabolic distribution of permeability in smear zone[J]. Journal of Geotechnical and Geoenvironmental Engineering. 2006, 132(7): 937−941.

[2] 鲍树峰, 莫海鸿, 董志良, 等. 考虑地下水位影响的砂井地基强度增长计算[J]. 岩石力学与工程学报, 2014, 33(6): 1269−1277. BAO Shufeng, MO Haihong, DONG Zhiliang, et al. Increment calculation of soil shear strength for sand drain foundations considering ground water level[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1269−1277.

[3] TANG Xiaowu, ONITSUKA K. Consolidation by vertical drains under time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739−751.

[4] TANG Xiaowu, ONITSUKA K. Consolidation of double-layered ground with vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(14): 1449−1465.

[5] 秦康, 卢萌盟, 蒋斌松. 砂井联合水泥土搅拌桩复合地基固结解析解[J]. 岩土力学, 2014, 35(增2): 223−231. QIN Kang, LU Mengmeng, JIANG Binsong. Analytical solution for consolidation of composite foundation with sand drains and cement-soil mixing piles[J]. Rock and Soil Mechanics, 2014, 35(S2): 223−231.

[6] 吴利科, 刘德进, 刘亚平. 长江口工程海上塑料排水板打设工艺及专用船的开发[J]. 水运工程, 2006, 397(12): 125−129. WU Like, LIU Dejin, LIU Yapin. Development of technology for offshore installation of plastic drains and plastic drain driving barge[J]. Port & Waterway Engineering, 2006, 397(12): 125−129.

[7] 杨京方, 诸葛爱军, 侯晋芳. 浅层地基加固中塑料排水板打设方法改进探讨[J]. 中国港湾建设, 2010, 166(2): 60−61. YANG Jingfang, ZHUGE Aijun, HOU Jinfang. Discussion on method of improving plastic vertical drain installation technique in surface soft clay improvement[J]. China Harbour Engineering, 2010, 166(2): 60−61.

[8] 潘金. 振动打桩机打设塑料排水板加固大面积软土地基工程实践[J]. 建筑技术, 2003, 34(3): 205−206. PAN Jin. Mass soft soil strengthened by draining plastic slab driven by vibration pile driver[J]. Architecture Technology, 2003, 34(3): 205−206.

[9] 单奕. 软基加固新型排水板打设装备开发探讨[J]. 港工技术, 2009, 46(6): 33−34. SHAN Yi. Discussion on development of new type of drainage plate-based equipment for consolidating soft soil foundation[J]. Port Engineering Technology, 2009, 46(6): 33−34.

[10] 谢康和, 余坤, 童磊, 等. 考虑影响区真实形状的竖向排水井地基固结解[J]. 岩土力学, 2011, 32(10): 2944−2950. XIE Kanghe, YU Kun, TONG Lei, et al. Analytical solution for consolidation by vertical drains considering actual shape of influence zone[J]. Rock and Soil Mechanics, 2011, 32(10): 2944−2950.

[11] 余坤. 考虑影响区真实形状的砂井地基固结理论研究[D]. 杭州:浙江大学建筑工程学院, 2010: 18−49. YU Kun. Study on the consolidation theory for vertical drains considering the actual shape of influence zone[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2010: 18−49.

[12] 刘加才, 施楚勇, 赵维炳, 等. 双层竖井地基半透水边界固结分析[J]. 岩土力学, 2007, 28(1): 116−122. LIU Jiacai, SHI Jianyong, ZHAO Weibing, et al. Consolidation analysis of double-layered ground with impeded boundaries using vertical drains for soil improvement[J]. Rock and Soil Mechanics, 2007, 28(1): 116−122.

[13] XIE Kanghe, XIE Xinyu, GAO Xiang. Theory of dimensional consolidation of two layered soil with partially drained boundaries[J]. Computers and Geotechnics, 1999, 24(4): 265−278.

[14] 李翔宇, 刘国彬, 刘铭, 等. 考虑半渗透边界的隧道周围超孔隙水压力消散解[J]. 岩土工程学报, 2014, 36(1): 75−82. LI Xiangyu, LIU Guobin, LIU Ming, et al. Analytical study on dissipation of excess pore water pressure around tunnels with semi-permeable boundary conditions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 75−82.

[15] 谢康和, 曾国熙. 等应变条件下的砂井地基固结解析理论[J]. 岩土工程学报, 1989, 11(2): 3−17. XIE Kanghe, ZENG Guoxi. Consolidation theories for drain wells under equal strain condition[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 3−17.

[16] 谢康和. 砂井地基: 固结理论、数值分析与优化设计[D]. 杭州: 浙江大学建筑工程学院. 1987: 13−46. XIE Kanghe. Drain well: consolidation theory, numerical analysis and optimum design[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 1987: 31−46.

[17] 吴慧琴, 李瑞杰, 张文虎. 舟山钓梁二期围垦工程潮流泥沙数值分析[J].水道港口, 2014, 35(1): 8−14. WU Huiqin, LI Ruijie, ZHANG Wenhu. Numerical analysis of tidal current and sediment on the secondary Diaoliang reclamation in Zhoushan[J]. Journal of Waterway and Harbor, 2014, 35(1): 8−14.

[18] 庄小将, 黄哲浩, 孙决策, 等. 温州石化基地围垦工程潮流物理模型试验研究[J]. 水道港口, 2008, 29(4): 253−258. ZHUANG Xiaojiang, HUANG Zhehao, SUN Juece, et al. Physical model test study on the reclamation project for Wenzhou Petrochemical Industry Base[J]. Journal of Waterway and Harbor, 2008, 29(4): 253−258.

[19] 刘国林, 王燕. 台州十一塘围垦工程石料海上高中低泊位装船技术[J]. 施工技术, 2013, 42(12): 93−95. LIU Guolin, WANG Yan. Shipment technology for stones at different berth on sea in Taizhou Eleven Pond Reclamation project[J]. Construction Technology, 2013, 42(12): 93−95.

[20] 刘润, 闫玥, 闫澍旺, 等. 模袋固化土围埝地基排水固结过程的模拟分析[J]. 岩土力学, 2007, 28(11): 2409−2414. LIU Run, YAN Yue, YAN Shuwang. Numerical simulation of consolidation process of soil foundation for a dam constructed by geobag solidified soil[J]. Rock and Soil Mechanics, 2007, 28(11): 2409−2414.

[21] 丁友斌, 陈海涛. 抛石围堰和模袋围堰在巢湖沿岸治理中的应用[J].华北水利水电学院学报, 2011, 32(1): 32−33. DING Youbin, CHEN Haitao. Application of riprap cofferdam and bag cofferdam in the ecological environment treatment[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2011, 32(1): 32−33.

[22] 范公俊, 贾延权, 王艳红. 几种围堰施工技术在连云港滩涂区的应用[J].水利水电科技进展, 2011, 31(1): 62−65. FAN Gongjun, JIA Yanquan, WANG Yanhong. Application of several kinds of cofferdam construction techniques in tidal flat of Lianyungang[J]. Advances in Science and Technology of Water Resources, 2011, 31(1): 62−65.

[23] 魏新江, 王金艳, 丁智, 等. 舟山海底沉管隧道模袋砂围堰位移分析[J]. 岩石力学与工程学报, 2013, 32(9): 1835−1842. WEI Xinjiang, WANG Jinyan, DING Zhi, et al. Displacement analysis of geomembrane bag with sand soil cofferdam in Zhoushan undersea immersed tube tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1835−1842.

[24] 邓彪, 郭小龙, 李志军. 南昌红谷沉管隧道江中模袋砂围堰冬汛灾后土石围堰重建施工技术[J]. 隧道建设, 2016, 36(9): 1114−1119. DENG Biao, GUO Xiaolong, LI Zhijun. Reconstruction technologies for earth-rock cofferdam after sandbag cofferdam hit by winter season in Ganjiang River: case study of Honggu Immersed Tunnel in Nanchang[J]. Tunnel Construction, 2016, 36(9): 1114−1119.

(编辑 陈爱华)

Solution and application of vertical drain consolidation theory considering a square influence area

NIU Ben1, 3, 4, TANG Xiaowu2, ZHANG Chaojie5, CHEN Xiuliang5

(1. CCCC Fourth Harbor Engineering Institute Co.,Ltd., Guangzhou 510230,China;2. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;3. Key Laboratory of Environmental Protection & Safety of Communication Foundation Engineering, CCCC, Guangzhou 510230, China;4. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China;5. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China)

A consolidation solution considering a square influence zone and boundary permeability was obtained. The results are different among consolidation theory with different shapes (including a square zone, a regular hexagonal zone and a circular zone). The result difference between a regular hexagonal zone and a circular zone is small but the result difference between a square zone and a circular zone is large. After considering the factor of time discretization and the factor of pore pressure transmission, the theory is applied to the estimation of degree of consolidation of soilbag filled with mud soil buried with PVD system. The estimation result shows a good coincidence with the FEM calculating result and shows some difference with the lab experiment result, which is within the margin of error. Analysis of the geometry parameter can improve draining of the soilbag system while analysis of the physical parameter can provide qualitative judgment.

square influence zone; boundary permeability; PVD; soilbag; consolidation

10.11817/j.issn.1672-7207.2017.05.022

TV3

A

1672−7207(2017)05−1283−10

2016−07−20；

2016−09−30

国家自然科学基金资助项目(51308310)；浙江省科技厅创新团队建设与人才培养项目(2011F2042)；浙江省自然科学基金资助项目(LQ13E080007) (Project(51308310) supported by the National Natural Science Foundation of China; Project(2011F2042) supported by the Science & Technology Department of Zhejiang Province on the Innovative Team Building and Personnel Training; Project(LQ13E080007) supported by the Natural Science Foundation of Zhejiang Province)

唐晓武，博士，教授，从事环境土工、软土地基等问题的研究；E-mail: tangxiawu@zju.edu.cn