透镜体影响尾矿坝安全性的规律及其简化方法

李志平，彭振斌，何忠明，袁维



透镜体影响尾矿坝安全性的规律及其简化方法

李志平1, 2，彭振斌1，何忠明3，袁维4

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 化工部长沙设计研究院，湖南长沙，410117；3. 长沙理工大学交通运输工程学院，湖南长沙，410114；4. 河北省建设勘察研究院，河北石家庄，050031)

对透镜体的参数敏感性进行分析，并提出一种透镜体简化分析方法，提高数值建模的效率。首先，将浸润线深度、坝顶位移和安全系数作为坝体安全的评价指标，把透镜体的大小、长短轴比、水平位置、垂直位置、黏结力和摩擦因数作为透镜体影响坝体的影响因子，通过正交试验设计方法探讨该6个影响因子对坝体安全的影响规律，然后，定义影响系数评价6个影响因子对安全性的影响程度，并通过主成分分析法和判别分析法建立透镜体简化的准则，并以此作为判据来决定各个透镜体是否从模型中忽略。研究结果表明：该简化方法在流程上可操作性强，所计算的安全系数具有一定的可靠性。

尾矿坝；透镜体；主成分分析法；判别分析法；稳定性分析

尾矿坝堆积体中通常夹杂着大量与周围尾矿砂具有不同强度和渗透性的小夹层，这类小夹层称为透镜体[1−8]。透镜体呈现无规律状态分布，从形态上看，透镜体通常表现为中间厚、两端薄的近似扁平椭圆形状。由于透镜体与周围主要尾矿砂的力学参数和渗透系数存在较大差异，影响尾矿砂正常沉积的连续性，可能会给尾矿坝带来一定的安全风险，主要存在以下3个方面的影响：1) 透镜体的渗透系数往往比周围沉积体的渗透系数大，大量透镜体的存在改变了库内地下水的正常渗透方式和路径，抬高坝体内浸润线的高度；2) 透镜体的强度参数和变形参数与周围沉积体的差别亦较大，对坝顶位移、潜在滑动面的形状和位置均会产生较大的影响；3) 在确定坝体内部各层的参数时，通常采用有限的钻孔取样方式，当沉积体的连续性较差时，目标层体的取样效果会受到较大的影响，从而影响参数的取值[4−12]。因此，在分析尾矿坝的稳定时，透镜体的影响不可忽略。但由于大量透镜体的存在给数值建模带来极大的困难，在保证安全系数计算精度的前提下对尾矿坝中的透镜体进行合理简化是值得研究的问题。目前单纯对透镜体安全性影响的研究成果较少，尚未形成一个广泛认可的透镜体简化方法。袁维等[3]对透镜体的安全性影响因素进行了系统研究，即采用正交试验设计方法将透镜体的影响因素分为2类：一类是几何因素，包含透镜体的大小(即透镜体面积与尾矿砂剖面面积之比)、位置和形状；另一类是参数因素，包含透镜体的渗透系数、强度参数和刚度参数，将以上影响因素设置为3个水平，并建立正交试验方案，然后基于熵权决策法探讨尾矿坝安全评价的主要指标，并研究透镜体对评价指标的影响规律。李苗等[13−14]对透镜体的简化方法进行了探讨，建议将强度参数大于周围沉积体强度参数的透镜体归并入周围土体，而将强度参数小于周围沉积体强度参数的透镜体保留下来。显然，这种简化方法具有明显的人为经验性，且只关注透镜体的强度参数与周围沉积体的差异，而忽略了透镜体的位置、大小等因素对尾矿坝安全性的影响。本文作者拟将浸润线深度、坝顶位移和安全系数作为尾矿坝安全性的3个评价指标，并根据袁维等[3]的建议，将透镜体的大小、水平位置、垂直位置、黏结力和摩擦因数作为透镜体影响坝体的影响因子，通过正交试验设计方法探讨该6个影响因子对坝体3个评价指标的影响规律，并基于主成分分析法和判别分析法建立透镜体的简化方法。最后，通过算例说明本文简化方法的操作流程和可靠性。

1 基本原理

1.1 主成分分析方法原理

主成分分析的主体思想是利用降维方法，在损失少量信息前提下，将多个指标转化为几个综合指标的多元统计方法。通常将转化生成的综合指标称为主成分，其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，使得主成分比原始变量具有某些更优越的性能。这样，在研究复杂问题时就可以考虑少量几个主成分而不至于损失太多信息，从而更容易抓住主要矛盾，揭示事物内部变量之间的联系，同时使问题得到简化，大大提高分析效率。假设对某个事物的研究设计到个评价指标，分别用表示，这个指标构成的维随机向量为，设随机向量的均值为，协方差矩阵为。对进行线性变换可以形成新的综合变量，用表示，即新的综合变量可以由原来变量线性表示，即存在下列变换关系：

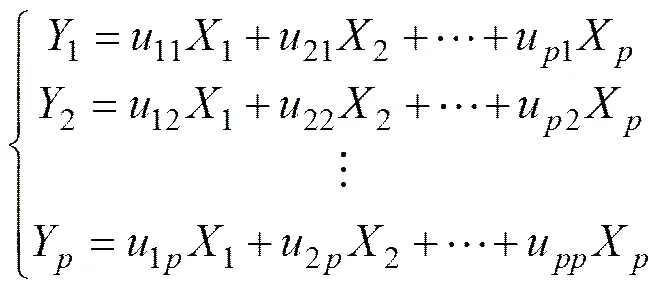
1.2 判别分析方法原理

回归模型普及性的基础在于用它去预测和解释度量变量。但对于非度量变量，一般的多元回归不适合解决这类问题，而判别分析法适用于被解释变量是非度量变量的情况。判别分析的主要目的是识别1个个体所属类别。在每种情况下，将对象进行分组，并且要求使用这2种方法中的1种可以通过人们选择的解释变量来预测或者解释每个对象的所属类别。当被解释变量是属性变量而解释变量是度量变量时，判别分析是合适的统计分析方法。判别分析的最基本要求是：1) 分组类型在2组以上；2) 每组案例的规模必须至少在1个以上；3) 解释变量必须是可测量的，这样才能够计算其平均值和方差，使其能合理地应用于统计函数。判别分析的假设条件主要如下：1) 每个判别变量(解释变量)不能是其他判别变量的线性组合；2) 各组变量的协方差矩阵相等；3) 各判别变量之间具有多元正态分布，即每个变量对于所有其他变量的固定值有正态分布。

2 基于单个评价指标的透镜体对尾矿坝安全性的影响

本文的透镜体模型参数见文献[3]。模型初期坝的内外坡比为1:2，其高度为29 m；堆积坝坝高为75 m，坝面的平均坡比为1:5.5，沉积滩平均坡比为2:100。分析正常水位情况下自重荷载作用的稳定性，计算模型与网格如图1所示。图1中4种材料采用不同的本构模型，透镜体和堆积坝采用邓肯张模型[16]，初期坝和基岩采用摩尔库仑模型，其基本物理参数见表1。

尾矿坝的稳定性包括渗流稳定性和力学稳定性。坝体符合渗流稳定性要求表明在内部孔隙压力作用下不会发生流土、管涌等渗透破坏，而渗透破坏最关键的影响因素是浸润线的深度。一般地，浸润线埋藏越浅，越容易发生渗透破坏；反之，则坝体发生渗透破坏的可能性越低。因此，渗透稳定性最直观的结果即为浸润线的位置；坝体符合力学稳定性要求包含2个方面：1) 变形符合要求；2) 不发生整体滑移破坏，即整体安全系数符合要求。坝体顶部通常是变形最显著的部位，可选择坝顶位移作为整体变形的评价指标。综上所述，在评价尾矿坝安全性时，选择浸润线深度、坝顶位移和安全系数是作为图1所示模型的安全性评价指标，分别用，和表示。透镜体对尾矿坝安全性产生影响的因子主要有6个：透镜体大小(即透镜体面积与尾矿砂剖面面积之比)、透镜体垂直位置、透镜体水平位置、长短轴比(即椭状透镜的长度与短轴长度之比)、透镜体黏结力比率和透镜体摩擦角比率，分别用，，，，和表示。每个影响因子取3个水平值，各个水平值见表2。

图1 计算模型网格图

正交试验设计方法是研究多因素多水平的一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的点进行试验。这些有代表性的点具备了“均匀分散，齐整可比”的特点，是一种高效率、快速、经济的实验设计方法[17−19]。尾矿坝的评价指标有3个，对评价指标产生影响的因子有6个，这里研究此6个影响因子对评价指标的影响规律，可根据正交试验方法来制定试验方案。显然，本试验为6因素3水平正交实验，根据正交实验表可知，共需要进行18次试验，各次试验的水平取值情况见表3。根据表3所示试验方案，共建立18个计算模型，采用有限元计算方法进行流−固耦合分析，得到各个试验方案的位移场、渗流场，并同时采用强度折减法计算各个方案的安全系数。为了深入探讨透镜体对尾矿坝安全性的影响规律，将18个试验方案的计算结果(浸润线深度、坝顶位移和安全系数)采用正交试验数据处理方法进行处理即可得到各个评价指标的极差，进而对参数敏感性进行分析。

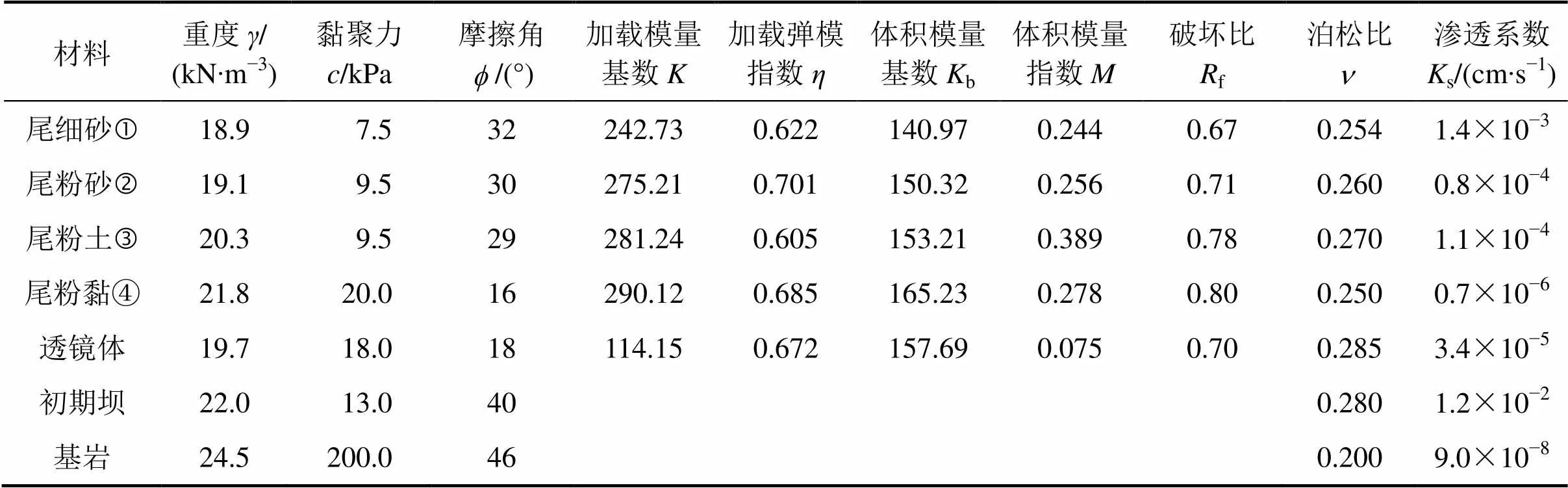
表1 土体计算参数取值

注：初期坝弹性模量取70.0 MPa，基岩弹性模量取5.0 MPa。

表2 不同影响因子的取值水平

注：透镜体的大小()用透镜体面积与尾矿砂剖面面积的比值表示；透镜体的垂直位置()用1，0和−1表示，分别代表透镜体紧靠沉积滩滩面、位于竖直方向的正中间、紧靠基岩；透镜体的水平位置()用1，0和−1表示，分别代表透镜体紧靠坡面、位于水平方向的正中间、紧靠模型的后缘；长短轴比()表示椭圆状透镜的长轴和短轴的长度比值；透镜体的黏结力()和摩擦角()分别用透镜体的黏结力、摩擦角与周围尾矿砂黏结力、摩擦角的比值表示。

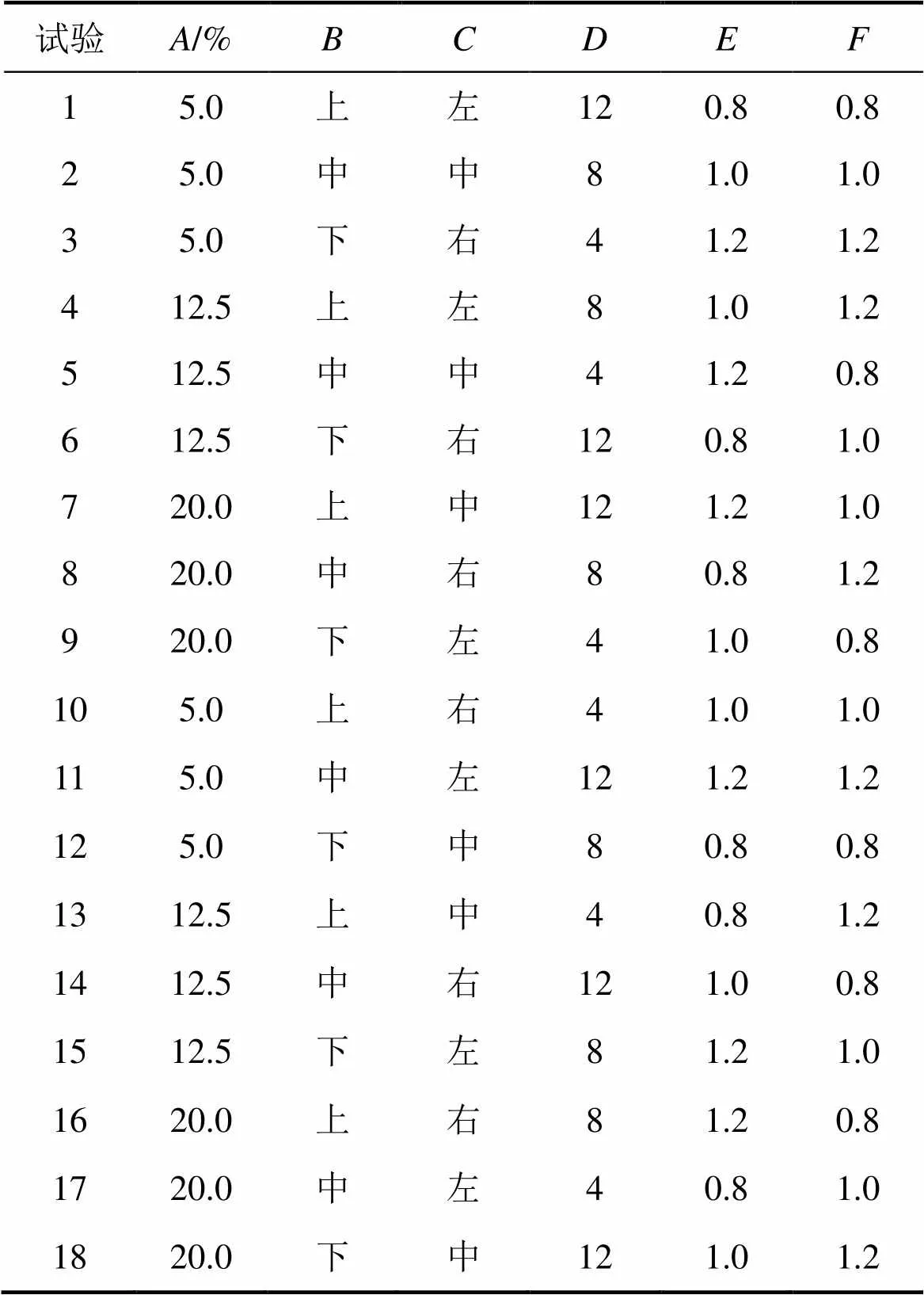
表3 正交试验方案

2.1 透镜体对浸润线深度的影响

对于浸润线深度而言，6个影响因素的极差排序如下：

R＞R＞R＞R＞R＞R(2)

显然，，和这3个影响因子的极差要显著大于，和的极差，表明透镜体面积、垂直位置和水平位置对浸润线深度的影响很显著，而透镜体的形状、抗剪强度参数对浸润线的深度影响较小，其中透镜体的水平位置对浸润线深度影响最大，而黏结力对浸润线深度影响最小。将以上6个因素3个水平对应的浸润线深度平均值绘制在同一张图上，如图2所示。由图2可知：随着透镜体面积增大，浸润线埋深呈整体减小趋势；透镜体埋深越大，浸润线深度先降低后增大，当透镜体在竖直方向的中间位置时，透镜体埋深最浅；在水平方向上时，透镜体越靠近坡面，浸润线埋深越浅；随着透镜体长短轴比增大，透镜体埋深先增大后减小，在比值为8.0时，埋深达到最大值；随着透镜体抗剪强度参数增大，浸润线埋深整体呈减小趋势，抗剪强度参数对浸润线埋深的影响是间接的，主要通过影响位移场间接对渗流场产生影响，体现了流固耦合模拟的特点。

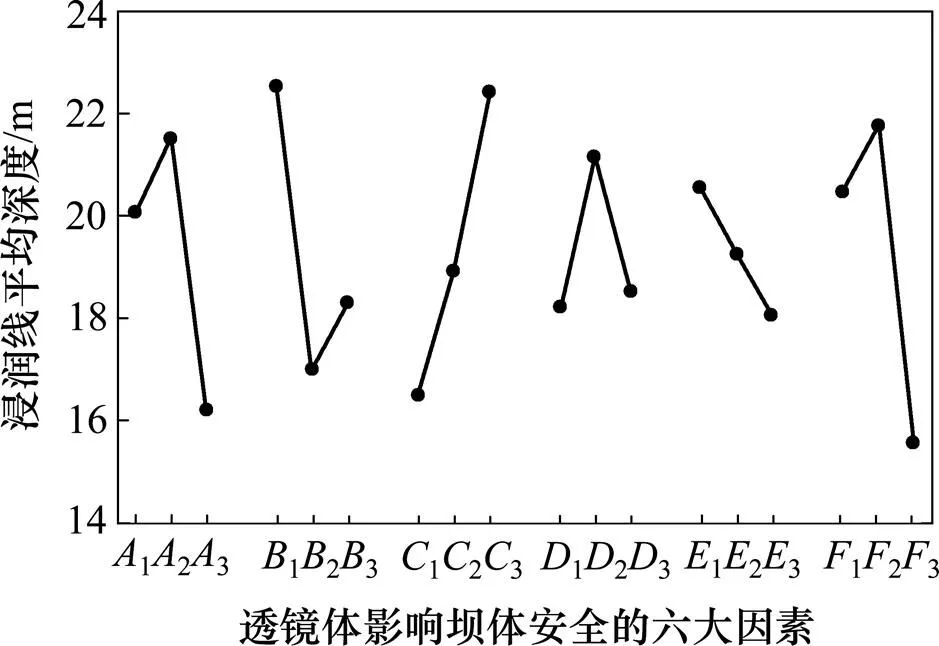
图2 浸润线平均深度与六因素关系

2.2 透镜体对坝顶位移的影响

对于坝顶位移而言，6个影响因素的极差排序如下：

R＞R＞R＞R＞R＞R(3)

显然，透镜体的面积对坝顶位移影响最大，透镜体的长短轴比次之，透镜体的垂直位置对坝顶位移影响最小。透镜体2个抗剪切强度参数对坝顶位移的影响要大于透镜体垂直位置的影响，但稍小于透镜体水平位置对坝顶位移的影响。将6个因素不同水平下的平均坝顶位移绘制在同一张图中，如图3所示。由图3可知：透镜体面积对坝顶位移的影响呈单调增大变化趋势，即透镜体面积越大，坝顶位移越大；透镜体垂直位置对坝顶位移的影响亦呈单调变化趋势，即随着透镜的深度增大，坝顶位移增大，但增大幅度不明显；对于透镜体水平位置而言，坝顶位移随着透镜体远离坡面，其值先增大后降低，当透镜体处于水平方向的中间位置时达到最大值；随着透镜体长短轴比降低，坝顶位移先呈整体增大趋势；黏结力和摩擦角对坝顶位移的影响规律是相同的，即随着抗剪切强度参数增大，坝顶位移逐渐减小。

图3 坝顶位移与6个因素之间的关系

2.3 透镜体对安全系数的影响

对于安全系数而言，6个影响因素的极差排序如下：

R＞R＞R＞R＞R＞R(4)

显然，透镜体的摩擦角、面积、黏结力以及透镜体的垂直位置4个影响因素的极差较接近，且比其他2个影响因素的极差要大，表明式(4)中前面4个影响因素对安全系数的影响较大，其中摩擦角对安全系数的影响最大；透镜体长短轴比和透镜体的水平位置对安全系数的影响较小，其中透镜体的水平位置对安全系数的影响最小。将以上6个因素不同水平下的平均安全系数绘制在同一张图中，如图4所示。由图4可知：随着透镜体面积增大，安全系数呈单调递减趋势；透镜体在竖直方向上，埋深越大，安全系数越大；透镜体在水平位置上的变化对安全系数的影响很小，大致先呈小幅度增大然后小幅度降低；随着长短轴比减小，安全系数先降低后增大，当长短轴比值为8.0时，安全系数取最小值；黏结力和摩擦角对安全系数的影响规律是一致的，即随着抗剪切强度参数增大，安全系数逐渐增大。

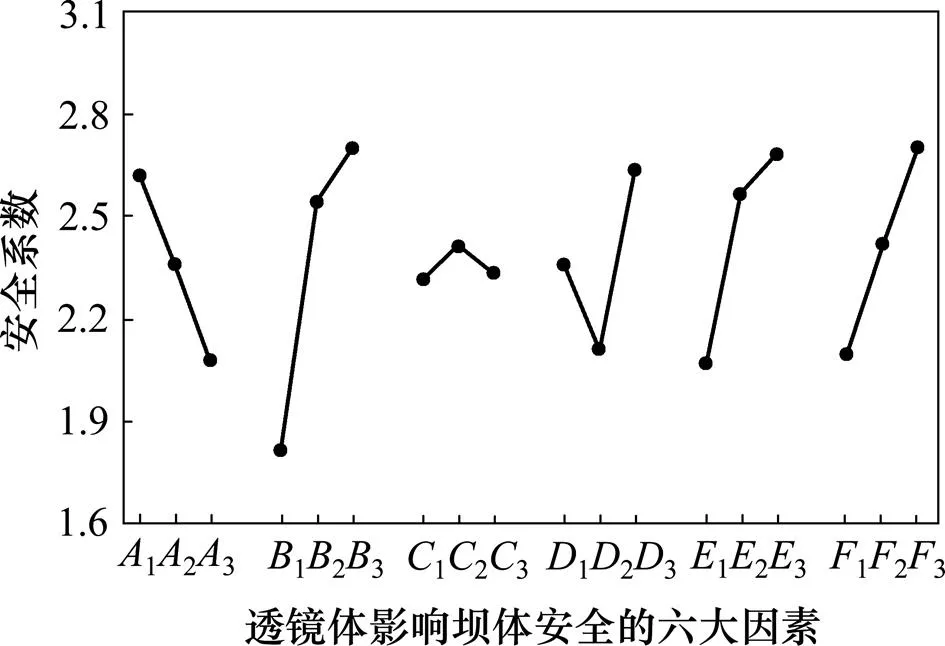
图4 安全系数与6个因素之间的关系

3 基于综合评价指标的透镜体对尾矿坝安全性影响规律

从透镜体对尾矿坝浸润线深度、坝顶位移和安全系数的影响规律可知，这3个评价指标可以从不同的角度对尾矿坝的安全性进行评估，而6个影响因素对不同评价指标的影响规律存在显著差异，且各个评价指标的显著影响因子各不相同。因此，有必要综合3个评价指标，尽可能得到1个综合评价指标，有利于找出对坝体安全性产生影响的显著影响因子。下面基于主成分分析法研究坝体安全性的综合评价指标，并基于该评价指标找出使坝体安全性处于最优状态的影响因子取值组合。

尾矿坝的安全性通常为浸润线深度、坝顶位移和安全系数，分别用符号1，2和3表示，通过主成分分析方法得到解释的总方差。第1个主成分解释了全部方差的88.467%，即包含了原始数据信息总量达88.467%，这说明用该主成分能评价尾矿坝的安全性。设这个主成分为1，则1可表示如下：

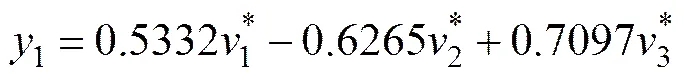
从1的线性组合可以看到：3个单项评价指标在综合因子1中所占比重较接近，但从评价指标系数绝对值看，第3个指标的系数绝对值最大，其次是2个指标的系数绝对值；第1个指标的系数绝对值最小，这表明第3个指标重要性最大，第2个指标的重要性次之，第3个指标的重要性最小，因而从另一个角度说明安全系数比其他2个指标的重要性大。

基于式(5)可以得到18个试验方案的综合评价指标(主成分)，采用前面相同计算方法便可得到综合评价指标的极差分析结果。对于主成分而言，6个影响因素的极差排序如下：

R＞R＞R＞R＞R＞R(6)

由此表明，透镜体大小()、透镜体抗剪切强度参数(和)是影响尾矿坝安全性的最主要因素。除以上3个因素之外，透镜体长短轴比()也对尾矿坝的安全性有一定影响，透镜体的位置(和)对尾矿坝的安全性影响较小。将以上6个因素3个水平对应的主成分平均值绘制在同一张图上，如图5所示。由图5可知：随着透镜体A(=1, 2, 3)增大，主成分平均值呈直线下降，表明透镜体大小()越大，尾矿坝的安全性越低；随着透镜体的垂直位置和水平位置发生变化，主成分平均值的变化幅度不明显，表明透镜体的位置对尾矿坝的安全性影响不大；随着透镜体抗剪切强度增大，尾矿坝的安全性明显提高。

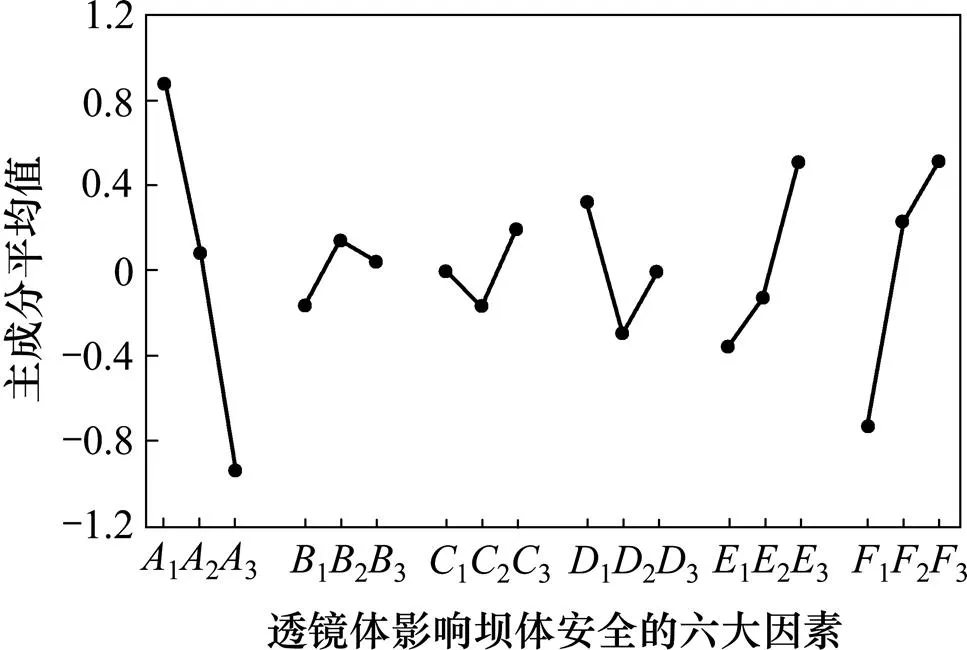
图5 主成分与六因素关系图

4 透镜体简化方法

为了对透镜体进行合理简化，需要考察算剖面存在透镜体与无透镜体时综合评价指标的差异，并根据此差异来判断透镜体进行简化。假设上述差异性用偏移系数来描述，偏移系数的定义如下：

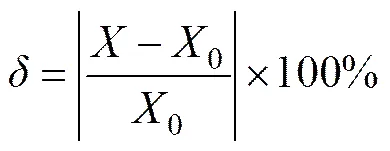
式中：为存在透镜体时的综合评价指标取值；0为计算剖面无透镜体时的综合评价指标取值。18个试验方案的偏移系数计算结果见表4。

一般而言，岩土工程中5%以内的偏差在可以接受范围内[20]，因此，偏移系数大于5%的透镜体不可忽略，而偏移系数小于5%的透镜体可以忽略。基于以上原则，建立判别分析的数据库，见表5。需注意的是：解释变量(透镜体垂直位置)取1表示透镜体位于竖直方向的顶部，取0表示位于竖直方向的中间，取−1表示位于竖直方向的底部；解释变量(透镜体的水平位置)取1表示透镜体位于水平方向的最左边，取0表示位于水平方向的中间，取−1表示位于水平方向的最右边；被解释变量表示是否需要考虑该透镜体对尾矿坝的影响，“YES”表示需要考虑，“NO”表示该透镜体可以略去。

基于以上数据库并通过SPSS软件的判别分析模块，对于任意1个给定的透镜体和计算剖面，便可判断该透镜体是否对计算结果产生影响，并进而判断是否可以将该透镜体从计算模型中略去。下面以1个简单例子来说明具体的操作流程。如图6所示，计算剖面的尺寸及尾矿砂、初期坝和基岩的取值与表1中的取值相同；透镜体的各项取值如下：=5%，=0.5，=−0.5，=8，=0.6，=0.9。

表4 各个试验方案的偏移系数计算结果

表5 判别分析数据库

通过SPSS进行判别分析，结果表明：在=5%，=0.5，=−0.5，=8，=0.6，=0.9时，判别返回值为“1”，表明该透镜体不能从计算模型中忽略。通过基于有限元流固耦合分析，无透镜体时的浸润线深度、坝顶位移、安全系数分别为21.38 m，0.60 m和2.61，有透镜体时的浸润线深度为24.51 m，4.70 m和2.78。根据式(7)，3个评价指标的偏移系数分别为14.6%，683%和6.5%，显然均大于5.0%，因此，此透镜体不能略去，与判别分析结果一致。

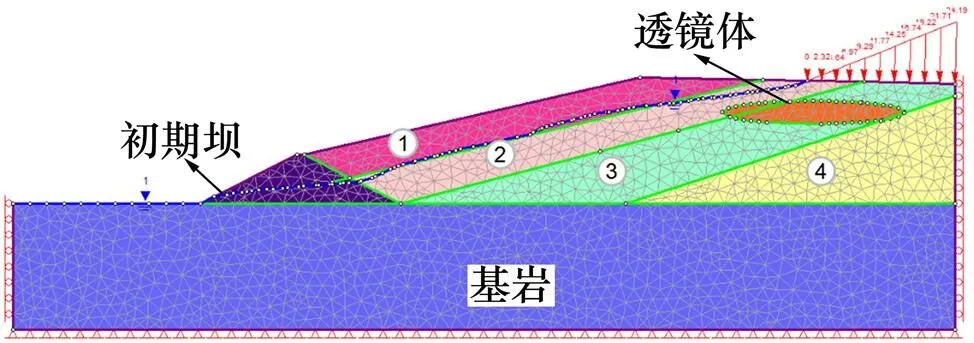
图6 计算模型网格图

综上所述，对透镜体简化的关键是建立基本的数据库，然后将待判别的透镜体数据输入数据库，通过判别分析法判断该透镜体是否可以从计算模型中略去，因此，透镜体简化的基本流程可按图7所示进行。

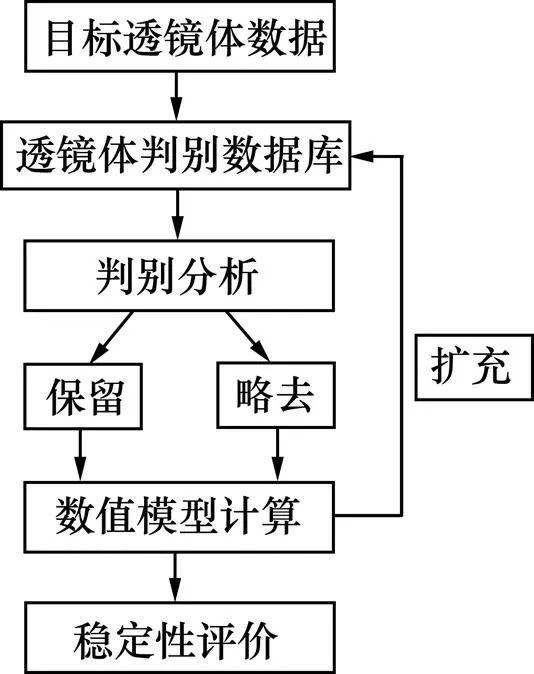
图7 透镜体简化流程

5 结论

1) 对于浸润线深度而言，透镜体面积小、垂直位置和水平位置对浸润线深度的影响很显著，而透镜体的形状、抗剪强度参数对浸润线的深度影响较小，其中透镜体的水平位置对浸润线深度影响最大，而黏结力对浸润线深度影响最小。对于坝顶位移而言，透镜体的面积对坝顶位移影响最大，透镜体的长短轴比次之，透镜体的垂直位置对坝顶位移影响最小，透镜体2个抗剪切强度参数对坝顶位移的影响要大于透镜体垂直位置的影响，但稍小于透镜体水平位置对坝顶位移的影响。对于安全系数而言，透镜体的摩擦角、面积、黏结力以及透镜体的垂直位置这4个影响因素的极差较接近，且比其他2个影响因素的极差要大，其中摩擦角对安全系数的影响最大；透镜体长短轴比和透镜体的水平位置对安全系数的影响较小，透镜体的水平位置对安全系数的影响最小。

2) 透镜体大小()、透镜体抗剪切强度(和)是影响尾矿坝安全性的最主要因素。除以上3个因素外，透镜体长短轴比()也对尾矿坝的安全性有一定影响，透镜体的位置(和)对尾矿坝的安全性影响较小。

3) 对透镜体简化的关键是建立基本的数据库，然后将待判别的透镜体数据输入数据库，通过判别分析法判断该透镜体是否可以从计算模型中略去。

4) 对于坝体安全性而言，安全系数是最重要的评价指标，坝顶位移次之，浸润线深度在此3个指标中的重要性最小。但这3个指标的重要性相差不大，因此，除了计算坝体的安全系数外，还应重视对坝顶位移和浸润线深度的监测。

5) 透镜体大小越大越不安全，透镜体越靠近临空面和沉积滩表面越不安全，因此，在采用上游法堆坝时，尽量使尾矿砂往沉积滩后缘排放；同时，在堆积坝加高过程中，要防止在沉积滩表面出现大的透镜体。

[1] 邓红卫, 叶茂, 吴彦霖. 基于GMS和Slide的透镜体数值模拟和敏感性研究[J]. 安全与环境学报, 2016, 16(1): 91−94. DENG Hongwei, YE Mao, WU Yanling. Numerical simulation for the sensitivity of lenticels based on GMS and slide[J]. Journal of Safety and Environment, 2016, 16(1): 91−94.

[2] 王飞跃. 基于不确定性理论的尾矿坝稳定性分析及综合评价研究[D]. 长沙: 中南大学防灾科学与安全技术研究所, 2008: 85−89. WANG Feiyue. Research on stability analysis and comprehensive assessment of the tailing dam based on the uncertainty theory[D]. Changsha: Central South University. Institute of Disaster Prevention Science Safety Technology, 2008: 85−89.

[3] 袁维, 李小春, 白冰, 等. 透镜体对尾矿坝安全性影响的参数敏感性分析[J]. 中南大学学报(自然科学版), 2013, 44(3): 1174−1182. YUAN Wei, LI Xiaochun, BAI Bing, et al. Parameters sensitivity analysis of lenticle impacting on tailing dam safety[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1174−1182.

[4] 梅国栋. 尾矿库溃坝机理及在线监测预警方法研究[D]. 北京: 北京科技大学土木与环境工程学院, 2015: 70−74. MEI Guodong. Research on mechanism and online early-warning method for tailings dam failure[D]. Beijing: University of Science and Technology Beijing. School of Civil and Environmental Engineering, 2015: 70−74.

[5] 于广明, 宋传旺, 潘永战, 等. 尾矿坝安全研究的国外新进展及我国的现状和发展态势[J]. 岩石力学与工程学报, 2014, 33(S1): 3238−3248. YU Guangming, SONG Chuanwang, PAN Yongzhan, et al. Review of new progress in tailing dam safety in foreign research and current state with development trent in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S1): 3238−3248.

[6] 颜学军. 上游法尾矿堆筑坝坝体沉积规律探讨[J]. 稀有金属与硬质合金, 2008, 36(2): 54−58. YAN Xuejun. Investigation on the depositing law of tailings dam by upstream damming[J]. Rare Metals and Cemented Carbides, 2008, 36(2): 54−58.

[7] 路荣博, 王涛. 上游法尾矿库溃坝事故致因分析及安全管理技术研究[J]. 长江科学院院报, 2009, 26(S): 112−117. LU Rongbo, WANG Tao. Safety management technique and accident-causing analysis of dam-failure in upstream tailing pond[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(S): 112−117.

[8] 王跃飞, 徐志胜, 董陇军.尾矿坝稳定性分析的模糊随机可靠度模型及应用[J]. 岩土工程学报, 2008, 30(11): 1600−1605. WANG Yuefei, XU Zhisheng, DONG Longjun. Stability model of tailing dams based on fuzzy random reliability[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(11): 1600−1605.

[9] 尹光志, 陈鹏, 魏作安, 等. 尾矿坝内透镜体对浸润线影响的数值模拟[J]. 矿业研究与开发, 2016, 35(3): 64−67. YIN Zhiguang, CHEN Peng, WEI Zuoan, et al. Numerical simulation for the effect on lens to saturation line in tailing dam[J]. Mining R&D, 2016, 35(3): 64−67.

[10] 沈小克, 蔡正银, 蔡国军. 原位测试技术与工程勘察应用[J]. 土木工程学报, 2016, 49(2): 98−117. SHEN Xiaoke, CAI Zhenggen, CAI Guojun. Applications of in-situ tests in site characterization and evaluation[J]. China Civil Engineering Journal, 2016, 49(2): 98−117.

[11] 敬小非, 尹光志, 魏作安, 等. 尾矿坝垮塌机制与溃决模式试验研究[J]. 岩土力学, 2011, 32(5): 1377−1386. JING Xiaofei, YIN Guangzhi, WEI Zuoan, et al. Model experimental study of collapse mechanism and broken mode of tailings dam[J]. Rock and Soil, 2011, 32(5): 1377−1386.

[12] 李夕兵, 蒋卫东, 贺怀建. 尾矿堆积坝透镜体分布状态研究[J]. 岩土力学, 2004, 25(6): 947−949. LI Xibing, JIANG Weidong, HE Huaijian. Study on distributing state of lenticle in tailings fill dam[J]. Rock and Soil Mechanics, 2004, 25(6): 947−949.

[13] 李苗, 张红军, 陈唐军, 等. 灰色−突变理论在尾矿坝失稳预测中的应用[J]. 矿业研究与开发, 2014, 34(5): 66−68. LI Miao, ZHANG Hongjun, CHEN Tangjun, et al. Application of grey−catastrophe theory in instability prediction for tailing dams[J]. Research and Develop, 2014, 34(5): 66−68.

[14] 费维水. 尾矿坝稳定性分析中的若干问题研究[D]. 昆明: 昆明理工大学建筑工程学院, 2012: 62−66. FEI Weishui. Studies on the stability of tailing dam[D]. Kunming: Kuming University of Science and Technology. College of Construction Engineering, 2012: 62−66.

[15] 何晓群. 多元统计分析[M]. 北京: 中国人民大学出版社, 2014: 41−43. HE Xiaoqun. Multi-variate statistical analysis[M]. Beijing: China Renmin University Press, 2014: 41−43.

[16] 郑颖人, 孔亮. 岩土塑性力学[M]. 北京: 中国建筑工业出版社, 2010: 35−36. ZHENG Yinren, KONG Liang. Geotechnical plastic mechanics[M]. Beijing: China Building Industry Press, 2010: 35−36.

[17] 方开泰, 马长兴. 正交与均匀试验设计[M]. 北京: 科学出版社, 2001: 35−50. FANG Kaitai, MA Changxing. Design of experiment based on orthogonality and orthogonality[M]. Beijing: Science Press, 2001: 35−50.

[18] 张富有, 李刘操, 徐松. 基于液化判别的尾矿坝动力稳定性分析[J]. 河海大学学报(自然科学版), 2012, 40(6): 648−652. ZHANG Fuyou, LI Liucao, XU Song. Dynamic stability analysis of tailings dam based on liquefaction evaluation[J]. Journal of Hohai University (Natural Sciences), 2012, 40(6): 648−652.

[19] 李兆炜, 胡再强. 基于渗流理论的尾矿坝坝体稳定性分析研究[J]. 水利与建筑工程学报, 2010, 8(1): 56−59. LI Zhaowei, HU Zaiqiang. Analysis of tailing dam’s stability based on seepage theory[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(1): 56−59.

[20] GB 50021—2001, 岩土工程勘察规范[S]. GB 50021—2001, Code for investigation of geotechnical engineering[S].

(编辑 陈灿华)

Simplification method of lenticles and its impact on safety of tailings dam

LI Zhiping1, 2, PENG Zhenbin1, HE Zhongming3, YUAN Wei4

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;2. Changsha Design and Research Institute of Ministry of Chemical Industry, Changsha 410117, China;3. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China;4. Hebei Research Institute of Construction and Geotechnical Investigation, Shijiazhuang 050031, China)

Based on the method of orthogonal test design, the sensitivity analysis of parameters of the lenticle was performed and a simplification method for lenticles was proposed to increase the efficiency of numerical modeling. Firstly, the depth of seepage line, the displacement of dam crest and the safety factor were considered as the evaluation indexes and the size, horizontal and vertical position, the ratio of major axis minor axis, cohesion and friction of lenticles were treated as impact factors, and the influence of these six impact factors on the safety of tailing dam was discussed through orthogonal experiment design method. An impact coefficient was defined to evaluate the impact degree of six impact factors to the safety of tailing dam, and the judge criterion was established through the combination of the principal component analysis and discriminant analysis. Based on this judge criterion, it was determined whether the lenticle is to be removed from the numerical model. The results show that the simplified method has strong operability in the process, and the calculated safety factor has certain reliability.

tailing dam; lenticles; principal component analysis; discriminant analysis; stability analysis

10.11817/j.issn.1672-7207.2017.05.027

TU457

A

1672−7207(2017)05−1326−09

2016−08−10；

2016−10−22

国家自然科学基金资助项目(51508042) (Project(51508042) supported by the National Natural Science Foundation of China)

李志平，博士，从事尾矿坝及岩土工程技术研究；E-mail: a1013234@qq.com