考虑参数随机性的焊点热疲劳失效分析

申海东，李志强，吴俊毅



考虑参数随机性的焊点热疲劳失效分析

申海东，李志强，吴俊毅

（北京航空航天大学 可靠性与系统工程学院，北京 100191）

目的研究电子产品焊点几何参数的随机性对焊点热疲劳寿命的影响。方法基于Coffin-Masson的修正式Engelmaier模型，建立考虑多参数随机性的引线型封装的焊点热疲劳寿命评估模型，并利用蒙特卡罗法对该模型的精确度进行验证。以SMT鸥翼型（gull-wing）TSOP062封装为例，将焊点几何参数的随机性对热疲劳寿命的影响进行量化分析。结果影响焊点寿命的几何参数离散系数越大，焊点疲劳寿命越小，随机变量越多，焊点热疲劳寿命下降的越明显，焊点高度是影响元器件热疲劳寿命的敏感参数。结论该方法在已知小批次产品的参数波动信息的情况下，能预测整批次产品的热疲劳寿命，极大地减少试验时间和成本，提高电子产品及装备的可靠性。

焊点；热疲劳；概率评估；蒙特卡罗

焊点热疲劳失效是表面贴装技术（Surface mount technology SMT）焊点的主要失效形式，热疲劳失效的一个重要原因是基板与元器件热膨胀系数失配（Cofficient of thermal expansion, CTE）。在温度载荷循环下，基板与元器件热膨胀幅度不同，导致焊点承受周期性应力应变，当非弹性形变累积到一定程度时，就会导致焊点最终失效[1]。国内外有关学者做了大量的研究，在预测焊点的热疲劳寿命方面取得了很多研究成果，并建立了相关模型。总的来说分为如下4种类型[2—3]：基于塑性（剪切）应变的焊点疲劳寿命模型；基于蠕变应变的焊点疲劳寿命模型；基于能量的焊点疲劳模型；基于断裂力学参量的焊点疲劳寿命模型。这些模型针对不同应用情况可以用来预测焊点的热疲劳寿命，从而作为提高电子产品可靠性的基础。已有研究表明，焊接工艺、材料性能参数和焊点几何形态均影响焊点热疲劳寿命，且导致焊点失效的参数不可避免地具有随机性和波动性[4]。由于上述传统故障物理模型均基于确定性常量参数，因此在应用上述模型时，无法确定焊点相关几何参数作为随机变量时对其热疲劳寿命的影响。

文中基于Engelmaier模型，建立了引线型封装焊点热疲劳寿命的概率预测模型。该预测模型考虑了焊点几何参数的随机性，可用于分析影响焊点热疲劳寿命的相关参数作为随机变量时对焊点可靠性的影响，从而避免了传统故障物理模型的局限性。

1 焊点热疲劳寿命预测模型

1.1 Engelmaier焊点热疲劳模型

在表面贴装型（SMT）元器件中，焊点有着固定元器件、电路导通和电信号传递的作用。研究表明，元器件组件中的失效，70%是由于封装失效引起的，而在电子封装失效中，焊点失效是主要的失效形式。对于焊点低周热疲劳寿命的预测，通常是通过确定焊点在温度循环试验下的非弹性应变或非弹性应变能量密度等方法来完成。截至目前，已有大量的学者提出相关模型来预测这一复杂的破坏过程，其中Coffin-Manson的修正式Engelmaier模型应用最为广泛，并被国际电子工业联接协会IPC所采用和推荐：IPC-SM-785，IPC-D-279和IPC-9701[5]。Engelmaier模型[6—7]如式（1）所示：

式中：f为平均疲劳循环寿命；Δ为非弹性应变范围；为疲劳延伸指数；f为材料参数。对于铅锡共晶软焊料f取0.325，对于无铅焊料f的取值参考文献[8—9]。sj的计算公式参考文献[10]。

(2)

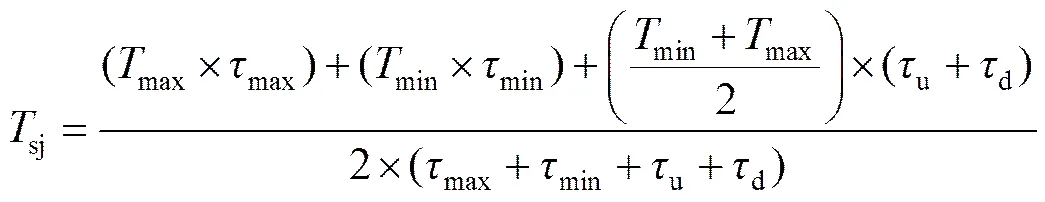
其中：

max=smax+cmax，min=smin+cmin，d=(max+min)/2。

式中：smax，cmax为高温驻留时间内基板和元器件的稳定温度；smin，cmin为低温驻留时间内基板和元器件的稳定温度；max为高温驻留时间；min为低温驻留时间；u为温升时间；d为温降时间。

当温度剖面中高低温驻留时间相等，且温升和温降时间相等时，公式（3）可简化为：

焊点非弹性应变范围求解如下：

(5)

式中：D为引线抗弯刚度[11]；为容差系数；D为元器件中心距；为焊点面积；为焊点高度；为马里兰大学Calce中心根据实验数据提出的修正因子。在文中，取0.746，取0.185。

1.2 简化几何模型

文中以SMT鸥翼型封装TSOP062为例，简化焊点分析模型如图1所示。共由四部分组成：PEM材料元器件、C197材料引线、62Sn36Pb2Ag焊料和FR4玻璃/环氧脂印刷电路基板。相关材料性能参数见表1。

图1 鸥翼型封装简化几何模型

表1 材料特性参数

2 焊点热疲劳可靠性的概率化评估

传统的焊点热疲劳寿命预测模型，如Coffin- Manson关系式，可以提供应变幅与疲劳循环周数之间的关系，但是这种确定论方法不能定量地分析各随机变量对焊点失效概率的影响程度，也不能提供产品失效率的信息。研究表明，许多焊点失效是由生产制造误差引起[12]。在实际情况下，焊接工艺导致焊点几何结构以及工艺参数将不可避免地出现不确定性，这些不确定性因素都将对产品的热疲劳寿命产生影响[13]。因而在产品设计过程中，可靠性预测必须考虑模型中随机变量的因素对疲劳寿命的影响。将焊点几何参数，以及元器件尺寸信息视为随机变量，采用魏鹤琳等[14]研究的方法建立了考虑多参数随机性的鸥翼型封装热疲劳寿命的评估模型，并基于蒙特卡罗模拟法对该模型的求解精确度进行了验证。

2.1 近似求解的建立方法

假设样本失效概率密度函数为()，由泰勒展开式可以得出该函数()的均值及方差。随机变量函数()在均值处的泰勒二阶展开式表示为：

(6)

如果已知任意随机变量的均值及方差，则随机变量函数的均值μ(x)及方差表示为：

(8)

当()随机变量函数为线性时，上述泰勒展开式近似求解()均值和方差的方法足够精确。对于非线性问题，上述方法的求解误差较大，甚至会得到完全错误的结果[15]，此时可用对数正态分布来提高该近似求解方法的精确度。研究表明，对于材料承受交变载荷直到出现低周疲劳破坏时，应变幅的离散情况用对数正态分布来描述，得到的疲劳寿命分布较为精确[16]。()的对数函数可以表示为：

式中：y=g(x)，，=1，2，…，；0，1，…，a为常数。

若将y视为正态分布，可得出其均值和方差，且当y的概率分布呈平滑过渡时，可以适用于概率密度中心极限理论。根据中心极限理论，ln()也必然服从正态分布[14]。事实上，概率中心极限定理并不要求每一个y完全服从正态分布。

2.2 蒙特卡罗方法

蒙特卡罗（Monte Carlo）方法，属于计算数学的一个分支，它通过数学分析和对随机变量的随机模拟来获得数学、物理、或工程应用等问题上的估计值。

假设来自同一分布函数相互独立的个随机变量1，2，…，x，且x的数学期望存在。那么对于任意的>0有：

2.3 近似求解方法精确性验证

采取上述方法建立焊点非弹性应变范围Δ的近似概率密度函数，并与蒙特卡罗模拟结果进行比对。设焊点几何参数以及元器件中心距D为相互独立且服从正态分布的随机变量，及。由式（３）及式（７）可得出焊点非弹性应变范围Δ的对数函数为：

根据式(6)，(7)，(11)，建立焊点非弹性应变范围Δ的近似概率密度函数为：

(12)

选择参数作为随机变量验证上述近似概率密度函数的精确度，当σ/μ=0.1，0.2，0.3时，近似概率密度函数与蒙特卡罗法模拟结果比较结果见图2。图2中μ=0.1 mm，曲线表示近似概率密度函数值，直方图表示为蒙特卡罗法模拟值。可以看出，近似值与模拟值吻合性较好，根据中心极限理论，随机变量越多，精确度也就越高。从而证明上述非弹性应变范围近似概率密度求解模型的精确度可以满足要求。

3 焊点热疲劳寿命可靠性分析

3.1 焊点热疲劳寿命概率评估模型

假设随机变量焊点高度，元器件中心距D和焊点面积均相互独立，且服从正态分布。根据上述求解方法，由式(1)，(7)，(8)建立焊点热疲劳预计寿命模型的概率密度函数近似式：

3.2 应用

以TSOP062表面贴装型封装为例，基于上述焊点热疲劳寿命概率密度近似式，并利用Engelmaier焊点热疲劳寿命评估模型，将焊点工艺参数的随机性对元器件热疲劳寿命的影响进行量化，评价各随机变量对焊点热疲劳寿命的影响。为了评价电子产品在实际工作环境中受温度的影响程度，温度循环测试采用常用的物理模拟方法。温度循环中，温变时间和高低温驻留时间是影响焊点寿命的重要因素。温度循环试验采用高温为100 ℃，低温为－30 ℃，高低温驻留时间为110 min，温升和温降时间为10 min。温度载荷剖面见图3。

该例中TSOP06元器件，μ=0.1 mm，μ=0.28 mm2，μD=30.2 mm。将它们视为相互独立且服从正态分布的随机变量，取σ/μ=0.1，σ/μ=0.15，σD/μD=0.1。由式(13)得焊点疲劳寿命概率分布，如图4所示。从图4a，b可以看出，随着离散系数（标准差/均值）的增大，焊点的疲劳寿命将降低；从图4a，c可以得出，鸥翼型封装热疲劳寿命对焊点高度信息更加敏感；从图4d可以看出，当随机变量参数增多时，焊点的热疲劳寿命的方差显著增加，焊点的可靠性明显降低。由此可见，焊点几何参数的随机性对焊点疲劳寿命的影响较大，因此建立焊点热疲劳概率评估模型对电子产品可靠性的研究非常必要。由此可以利用小批量产品焊点几何参数的波动信息以及小样本试验数据获得整批次样品的焊点热疲劳寿命分布，从而控制生产质量，保证整批次产品的合格率，减少维修成本。

4 结论

1）基于Coffin-Mason的修正式Engelmaier模型，建立了SMT引线型封装考虑多参数随机性的焊点热疲劳寿命评估模型，该模型适用于所有鸥翼型封装电子产品的热疲劳失效分析。

2）针对焊点非弹性应变范围，利用蒙特卡罗法验证了建立的焊点热疲劳寿命评估模型的精确度满足实际工程需要。

3）以TSOP062元器件为例，研究了影响焊点热疲劳寿命的几何参数作为随机变量时对焊点寿命的影响。

[1] 林健, 雷永平, 赵海燕. 电子电路中焊点的热疲劳裂纹扩展规律[J]. 机械工程学报, 2010, 46(6): 120—125.

[2] LEE W W, NGUYEN L T, SLEVADURAY G S. Solder Joint Fatigue Models: Review and Applicability to Chip Scale Packages[J]. Microelectronics Reliability, 2000, 40: 231—244.

[3] LI Xiao-yan, LI Zhi-qiang, SHEN Hai-dong, et al. The Analysis on Thermal Fatigue Life of LCCC Package Based on Strain Fatigue Model and FEM[C]// Prognostics and System Health Management Conference. 2015.

[4] CHEN Y, XIE L, KANG R. Probabilistic Modeling of Solder Joint Thermal Fatigue With Bayes[C]// Proceeding of the 2012 IEEE IEEM. 2012.

[5] CHAUHAN P, PECHT M, OSTERMAN M, et al. Critical Review of the Engelmaier Model for Solder Joint Creep Fatigue Reliability[J]. IEEE Transactions on Components and Packaging Technologies, 2009, 32(3): 693—700.

[6] ENGELMAIER W. Fatigue Life of Leadless Chip Carrier Solder Joints during Power Cycling[J]. IEEE Trans Compon Hybrids Manuf Technol, 1983, 6(3): 232—237.

[7] ENGELMAIER W. Surface Mount Solder Joint Reliability Controlling the Thermal Expansion[J]. International Electronic Manufacturing Technology Symposium, 1988: 62—65.

[8] ENGELMAIER W. Solder Creep-fatigue Model Parameters for SAC & SnAg Lead-free Solder Joint Reliability Estimation[C]// As Originally Published in the IPC Proceedings. 2009.

[9] ENGELMAIER W. Update on Lead-free Solder Joint Reliability[J]. Global SMT & Packaging, 2008, 8(2): 13—17.

[10] ZHANG G, KWAN C, XU R, et al. An Enhanced Prognostic Model for Intermittent Failures in Digital Electronics[J]. Aerospace Conference, 2007: 1—8.

[11] KOTLOWITZ R W. Comparative Compliance of Representative Lead Designs for Surface-mounted Components[J]. IEEE Transactions on Components, Hybridsand Manufacturing Technology, 1989, 12(4): 431—448.

[12] VLAHINOS A, O'KEEFE M. Sensitivity of Solder Joint Fatigue to Sources of Variation in Advanced Vehicular Power Electronics Cooling[J]. American Society of Mechanical Engineers, 2010: 45—53.

[13] JURGEN W, ELENA Z. Probabilistic Analysis of the Influences of Design Parameter on the Reliability of Chip Scale Packages[C]// 7thInt Conf on Thermal, Mechanical and Multiphysics Simulation and Experiments in Micro-Electronics and Micro-systems. EuroSimE, 2006.

[14] 魏鹤琳, 王奎升. 焊点热疲劳多模式失效寿命分析[J]. 机械工程学报, 2011,47(10): 70—75.

[15] ADDURI P. Robust Estimation of Reliability in the Presence of Multiple Failure Modes[D]. Dayton: Wright State University, 2006.

[16] 茆诗松, 汤银才, 王玲玲. 可靠性统计[M]. 北京: 高等教育出版社, 2008.

Thermal Fatigue Failure of Solder Joints Considering Randomness of Parameters

SHEN Hai-dong, LI Zhi-qiang, WU Jun-yi

(School of Reliability and System Engineering, Beihang University, Beijing 100191, China)

Objective To research influences of geometric parameters on the thermal fatigue life of solder joints. Methods Based on the Engelmaier model, the variant form of Coffin-Masson’s and lead package of multiparameter randomness, a solder fatigue life probability evaluation model was established. Monte Carlo method was adopted to verify the accuracy of the model. SMT (Surface Mount Technology) gull-wing TSOP062 package was taken as an example. Quantitative analysis on influences of geometrical parameters of solder joints on thermal fatigue life was carried out. Results The fatigue life of solder joint decreased with the increase of geometric parameters discrete coefficient. The more random variable of geometric parameters, the lower reliability of solder joints. The height of welder joint was a sensitive parameter which affects the thermal fatigue life of elements. Conclusion This method can predict the whole batch thermal fatigue life of products, reduce the test time and cost greatly, and improve reliability of product and equipment on the premise that information on parameter fluctuation of small batch product is obtained..

solder joint; thermal fatigue; probability evaluation; Monte Carlo

10.7643/ issn.1672-9242.2017.04.020

TJ01；TG405

A

1672-9242(2017)04-0096-05

2016-11-8；

2016-11-15

申海东（1991—）,男，湖南人，硕士, 主要研究方向为可靠性与环境试验技术。

李志强（1970—）,男，北京人，高级工程师，主要研究方向为可靠性与环境试验技术。