模仿神经元网络抗扰特性的电磁防护仿生研究

满梦华，蔡娜，马贵蕾，王震



模仿神经元网络抗扰特性的电磁防护仿生研究

满梦华1，蔡娜2，马贵蕾1，王震3

（1.军械工程学院 静电与电磁防护研究所，石家庄 050003；2.军械技术研究所，石家庄 050003；3.廊坊市健康教育研究所，河北 廊坊 065000）

目的研究神经元在噪声干扰环境下信息处理的抗扰特性，为电磁防护仿生研究提供有益借鉴。方法利用Hodgkin-Huxley模型建模神经元电信号的产生，结合S空间编码理论分析神经信息的表达。在此基础之上，研究神经信息处理在噪声干扰环境下的抗扰特性。建立具有噪声耦合方式的神经元数学模型，并在不同噪声强度下，计算神经元输出电信号对输入刺激的S空间编码，讨论噪声对编码的影响。结果在S空间中，神经元将输入刺激信号编码成符号序列，符号序列间的排序关系与输入信号频率间的排序关系所对应。输入噪声能够改变符号序列的值，但并没有改变符号序列间的排序关系，从而不会影响神经元在S空间中所表达的信息。结论 S空间编码是神经元抵御输入噪声干扰的一种重要机制，值得电子系统借鉴，以提高其抗扰能力。

S空间编码；Hodgkin-Huxley模型；噪声；抗扰

信息化条件下，交战双方以军事电子技术和信息技术为基础，在信息领域进行对抗。为了提高武器装备的信息化水平，微电子技术得以广泛运用，亦导致信息化装备对于各种电磁能量越来越敏感。随着诸如雷达、通信、导航等各种电磁辐射源功率的不断加大和频谱增宽，以及系统自身的电磁辐射与静电等问题，使得武器装备面临着更加复杂和恶劣的电磁环境。因此，传统的电子系统抗扰和防护方式面临着严俊的挑战。

据报道，21世纪上叶（约2020~2050年）将会发生第六次科技革命。这场革命是以生命科学为基础，融合信息科技和纳米科技，为解决和满足人类精神生活和生活质量的需要提供的最新技术。主体内容包括“整合和创生生物学”、“思维和神经生物学”、“生命和再生工程”、“信息和仿生工程”、“纳米和仿生工程”等。其中，《科学时报》对108位两院院士进行的问卷调查结果显示，信息和仿生工程的支持率最高，达到72%。由此可见，对于生物信息机理的仿生研究在科技发展中的主体地位已得到学术界的广泛认同。

电磁防护仿生研究正是通过探索生物体电磁信息传递的抗扰机理，将生物抗扰机制引入电子设计领域，突破本征特性领域转换的关键技术，提出武器装备电磁防护仿生的新原理和新方法，为电子装备提供有别于传统方式的设计思想、工作原理和体系结构，以提高其在复杂电磁环境下的可靠性与适应性，为解决电磁干扰与毁伤问题提供一种全新的技术支撑。

神经系统工作在一个充满噪声的环境中，无论是对外界环境的感知，内部信号的传递，还是肌肉动作的控制，噪声干扰普遍存在于神经信息处理的各个环节。其面临的噪声源可以归纳为三类：在神经突触传导信号时引入的噪声，即突触噪声；由神经细胞膜上离子通道引入的噪声，即通道噪声；外界输入信号所包含的噪声，即输入噪声[1—3]。这些噪声会导致神经元产生动作电位信号的时间和间隔发生变化，但从未影响神经信息处理的功能。例如，成千上万只蝙蝠栖息于同一山洞之中，它们共用同频段声波进行观察与交流，但从未发生类似多部“雷达”或“电台”间的同频干扰现象，大脑的神经细胞每天都有凋亡，但是其生理功能依然正常[4—5]。

神经系统的这一抗扰特征已逐渐成为神经生物学领域的研究热点。Gong等人研究了高斯噪声与非高斯噪声对神经系统的影响[6]。Sakumura等人研究发现，一定强度的噪声反而能够增强大脑信息处理信息的能力[7]。Liang等人研究发现，兴奋神经元在相位噪声输入下依然可以识别信号[8]。童勤业等人研究了听觉哺乳动物的听觉系统可以在复杂环境中识别信号，抵抗干扰[9]。上述研究揭示了神经系统的抗扰现象，但并未从神经信息处理的角度探寻神经抗扰的原理，解释噪声引起神经信号的变化却没有影响信息表达的原因。

神经编码是理解神经信息处理机制，分析抗扰特性时所面临的首要问题。目前，频率编码[10—12]和时间编码[13—15]得到普遍认可。其中，文献[9]提出的S空间编码属于时间编码范围，其对神经元动作电位序列进行精确的定量分析，为研究神经信息处理抗扰机制提供了有效的途径。文献[16]利用S空间编码研究蝙蝠听觉神经系统处理多普勒信号时，发现背景环境造成神经元输入信号的轻微抖动并没有影响其信息处理能力。

文中主要利用S空间编码理论和神经元电信号模型，研究神经信息处理的抗扰特性。基于神经元Hodgkin-Huxley模型建立噪声环境下神经元信息处理的数学模型，并对不同输入信号进行编码分析，在不同噪声强度下，讨论噪声对编码的影响。

1 方法

首先，利用数学建模的方法对神经系统进行建模，并构建噪声环境下的神经元计算模型。在S空间编码理论的指导下，利用圆映射与符号动力学的基本方法对神经元模型的结果进行编码计算。最后，利用S空间编码分析神经模型的抗扰性。

1.1 噪声环境下神经元模型建模

由于S空间编码是针对神经元的输入输出信号进行编码，单一神经元即可实现编码。采用经典的Hodgkin-Huxley模型对神经元建模[17—20]。该模型包括4个方程和10个参数，完备描述了产生动作电位所发生的通透性变化，可以描述神经纤维细胞膜电流、膜电压关系，解释了神经元动作电位产生和传导的机理，为研究神经信息的处理机制奠定了理论基础。

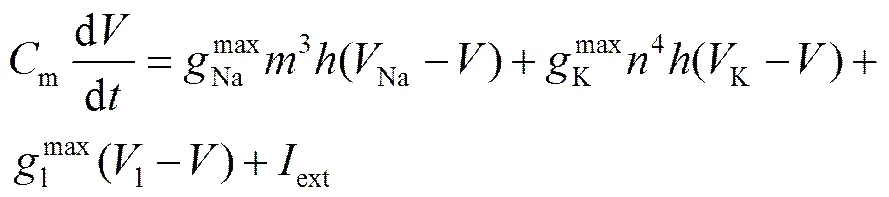
(2)

(3)

式中：ext为外部信号输入；为膜电压；m为膜电容；Na，K，l分别是钠离子、钾离子和漏电流通道的电导最大值，Na，K，l分别是相应通道的逆转电位；和为钠离子通道的门控变量，为钾离子通道的门控变量；∞()，∞()，∞()和τ()，τ()，τ()分别代表，，的饱和值和时间常数。

神经信息传递的载体是动作电位序列，单个动作电位具有“全或无”的特点，其幅值并不携带信息，整个序列中各动作电位的间隔表达信息。因此，在模型计算中，将神经元输入信号进行简化，将一串方波脉冲作为神经元模型的输入ext。

式中：amp为方波脉冲幅值；为脉冲幅值持续时间；0为方波脉冲的周期；为周期数。在文中，amp为20 μA/cm2，为1 ms，0取值为1.2~4.2 ms，间隔为0.2 ms。从而，信号的频率0取值为238.1~833.3 Hz。

将ext的周期0叠加强度为、均值为0的随机序列()来实现输入信号ext周期的随机波动，模拟神经元受到的噪声干扰。受噪声干扰的ext周期的计算为：

(6)

式中：T为未受干扰的周期；()表示强度为、均值为0的随机序列。在文中强度取值为0~0.4，间隔为0.1。不同噪声强度下的ext的频率如图1所示。

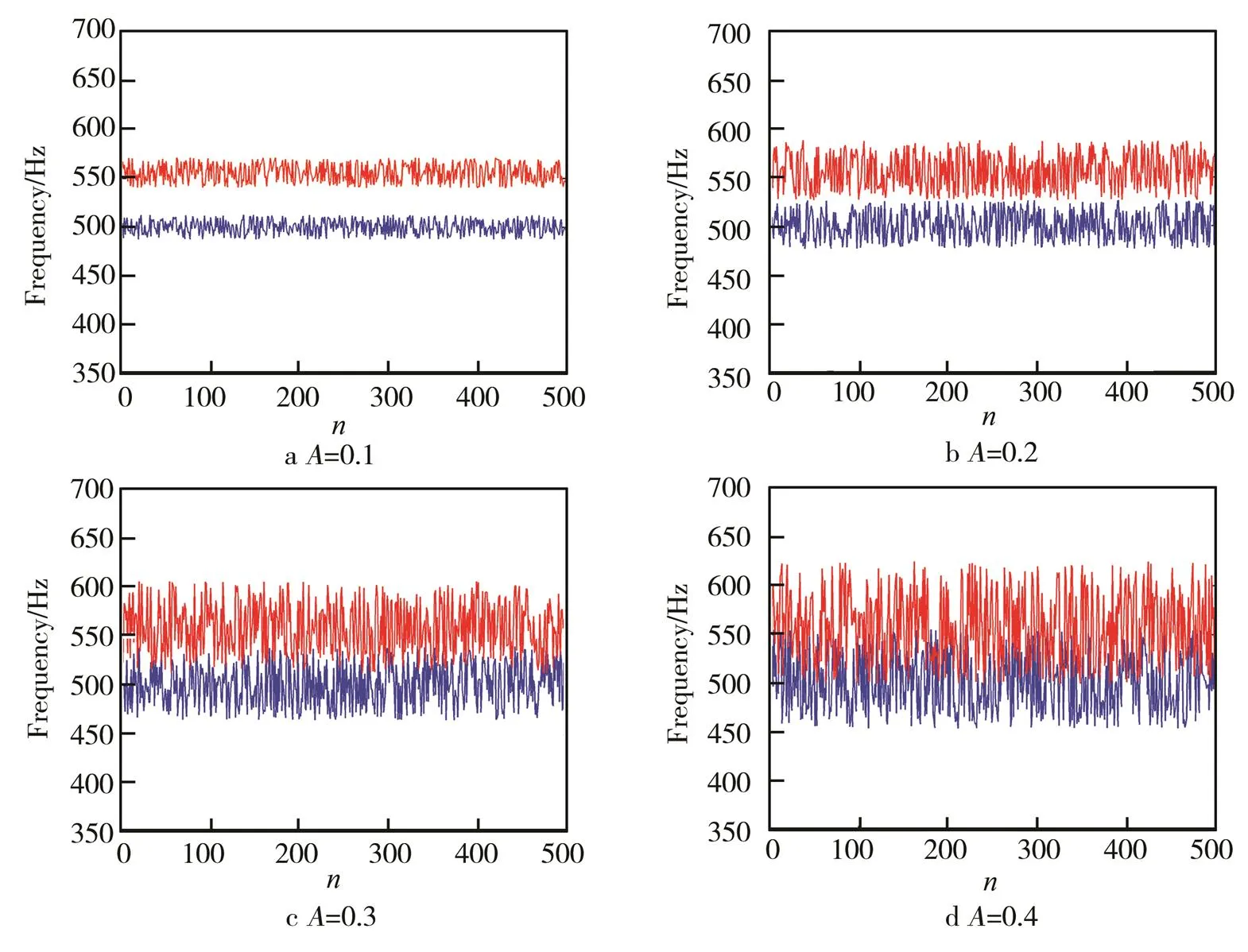
图1 不同噪声强度下输入信号频率随时间变化

1.2 S空间编码

S空间是基于动作电位序列的可排序性提出的，因为神经系统接收到的外界信号都具有排序性，比如声音的大小、光的明暗、气味浓淡等。动作电位序列就是这些信号在神经系统中的反应，因此，动作电位序列集合构成的序列空间也应该是可排序的。S空间编码可以通过对动作电位序列进行计算变换，将神经信息转化到一维有序空间中，然后对神经信息进行研究。

S空间编码主要分两步进行[21]。

1）利用圆映射转换方法判断神经系统的状态是否适合S空间编码，即输入信号对应的圆映射轨迹应该是单调提升的。如图2所示，图2a是神经元在恒频率方波脉冲刺激下产生的动作电位序列，经过圆映射计算可变换为图2b的圆映射轨迹，该轨迹是单调提升的，因此可以进行S空间编码。

2）利用符号动力学的分析方法完成编码。首先，利用神经元输入信号和输出动作电位计算符号序列。动作电位相邻峰峰值之间输入信号脉冲的个数P即是一个符号。由此，神经元输入信号和输出动作电位之间的关系就转化为一串符号序列：{1，2，3，…P，…}。

然后判断符号序列的序关系和输入信号的序关系，不同的输入信号频率对应不同的符号序列。假设在频率分别为f和f的输入信号刺激下，可以得到两串符号序列和：

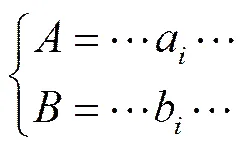
式中：a，b是符号序列中的符号。通过比较符号序列和中第一个不相同符号的大小，得到符号序列的序关系。该序关系对应输入信号频率的序关系，实现序空间编码。符号序列和之间的符号距离为[9]：

式中：表示符号序列中出现的最大符号；代表符号序列符号的编号。从符号距离定义的公式发现，越排在符号序列起始位置的符号，对符号距离的贡献就越大，后续符号对距离的贡献呈指数形式衰减。

2 结果与讨论

对噪声环境下的神经元模型进行仿真计算，计算时间为1000 ms。计算完成后对结果进行S空间编码计算，得到符号序列。结果发现，当神经元输入信号频率在312.5~833.3 Hz范围内，圆映射轨迹符合周期或准周期运动，计算出的结果满足S空间编码条件，可以进行S空间编码。当频率为250~312.5 Hz时，系统输入输出关系为锁相，符号序列相同，无法编码分辨。当频率为238.1~250 Hz时，系统输入输出关系为混沌状态，不适合进行符号编码。

当信号频率在312.5~833.3 Hz时，不同噪声强度输入信号的符号序列结果见表1—表5。通过比较任意两串符号序列中出现的第一个不同符号，得出两串符号序列的序关系。由表1—表3可知，当输入信号无噪声和噪声强度在0.1~0.2范围内时，随着输入信号频率的减小，符号序列递减，即输入信号频率的序递减，符号序列的序递减，两者之间的序关系一致。由此，S空间编码完成了神经信息的表达。

可以发现，表2和表3中一些相同频率的信号对应的符号序列不同，噪声的存在改变了符号序列中的符号值，但是在噪声强度0.1和0.2条件下，输入信号频率的序和符号序列的序依然一致。在噪声强度为0.3和0.4条件下，随着输入信号频率的减小，符号序列不再一致，符号序列的序关系出现错误。因此，一定强度的噪声虽然改变了符号序列中的符号值，但没有改变其序关系，从而不会影响其信息表达。

表1 无噪声条件下输入信号对应的符号序列

表2 噪声强度为0.1条件下输入信号对应的符号序列

表3 噪声强度为0.2条件下输入信号对应的符号序列

表4 噪声强度为0.3条件下输入信号对应的符号序列

表5 噪声强度为0.4条件下输入信号对应的符号序列

对符号序列进行距离计算，以频率为833.3 Hz的信号的符号序列为基准点，分别计算各频率信号与频率为833.3 Hz的信号之间的符号序列距离，如图3所示。无噪声和噪声强度在0.1~0.2时，随着频率差的增大，符号序列距离增大。噪声强度在0.3和0.4时，由图4可以发现，频率差为378.8 Hz的信号对应的距离小于频率差为333.3 Hz的信号。即随着频率差的增大，符号序列距离有时减小。可见，只有在符号序列的序未改变的情况下，符号序列的距离才会随着频率差的增大而增大。

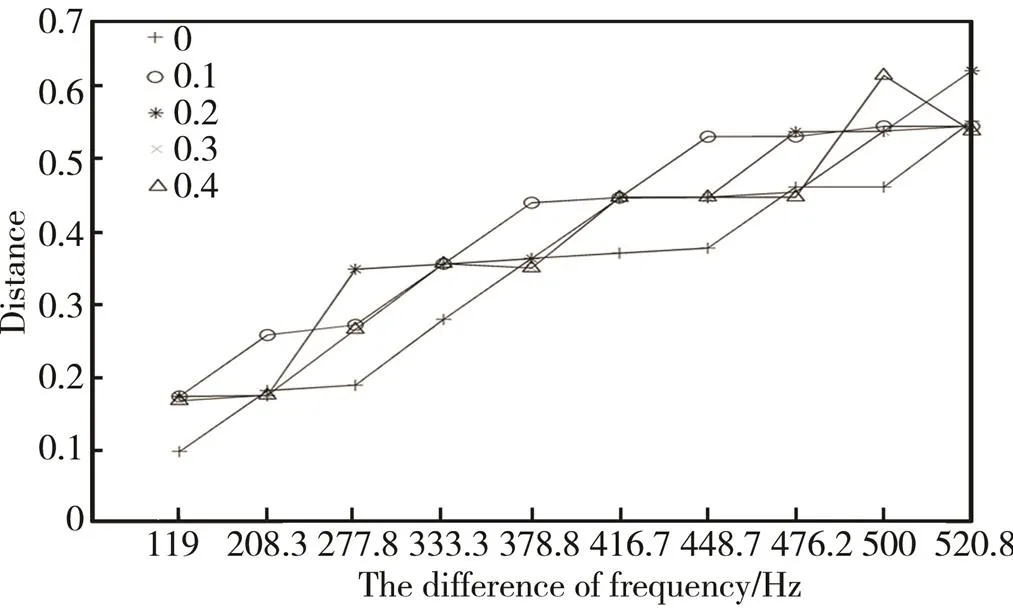
图3 噪声环境下不同频率差和符号序列距离关系

图4 不同频率差下噪声强度和符号序列距离关系

如图3所示，在噪声强度为0.1~0.2范围内时，噪声未影响符号序列间的序关系，但噪声强度改变了S空间距离。如在频率差为277.8 Hz下，不同噪声强度下的距离不同。即在符号序列的序和频率的序都确定的情况下，符号序列的距离不定。这体现了S空间的特点，在S空间中，只要序是确定的，符号序列之间的距离是可变的，距离的改变不会影响序关系。因此，S空间编码允许符号序列产生一定的距离变化，但是其序关系可以不变，即S空间编码可以抵抗一定强度噪声的影响。

在噪声强度达到0.3时，S空间编码不能正确处理信息，而在强度为0.2时则可以。由图1可以发现，噪声强度为0.3时，由于噪声强度的增大，输入信号的频率产生重叠，即输入信号的频率已不具备排序性，故单纯利用S空间编码无法将其正确排序。S空间编码正确分辨信息的前提条件是分辨的信息因素具有基本排序性。也就是说，只要噪声强度没有改变输入信号频率的序关系，输入的带干扰信号还是具有排序性的，S空间编码依然可以正确编码带有噪声的输入信号。

神经系统很有可能是在S空间处理信息的，S空间最大的特点是只有序的关系，而不用量的关系。即S空间中两点之间的距离可以任意变化，只要不改变两者之间的大小关系，其表达的信息就没有改变。因此，只要干扰噪声不影响环境信号的序关系，神经系统就可以通过S空间编码正确处理信息，大大降低了对输入信号的要求。这种信息处理方式为电子系统的电磁防护仿生研究[22—24]提供了有益的借鉴。电子系统是在笛卡尔坐标空间中处理信息的，其利用信号间的序关系和距离关系来表征信息，即笛卡尔坐标空间中两点之间的距离和大小关系都未改变，才能表现相同的信息。这对环境干扰较为敏感，即便是一个很小的电磁干扰信号，就足以影响其信息的表达。因此，在电磁防护仿生研究中，可以模仿S空间编码理论，提高电子系统对于电磁干扰的抵御与适应能力。

3 结论

文中基于神经元Hodgkin-Huxley模型和S空间编码方法，建立了噪声环境下神经元信息处理的简单模型，并对不同输入信号进行编码分析，研究了不同噪声强度对S空间编码的影响。S空间编码具有抗扰性，这是神经系统抗扰能力的一种体现，神经系统可以利用S空间编码抵抗干扰对信息处理的影响，其抗扰特点如下。

1）在S空间中，神经元将输入刺激信号编码成符号序列，符号序列间的排序关系与输入信号频率间的排序关系相对应。输入噪声能够改变符号序列的值，但并没有改变符号序列间的排序关系，从而不会影响神经元在S空间中所表达的信息。

2）S空间编码正确分辨信息的前提条件是分辨的信息因素具有基本排序性。也就是说，只要噪声强度没有改变输入信号频率的序关系，输入的带干扰信号具有排序性，S空间编码就可以正确编码带有噪声的输入信号。

3）结合S空间编码计算分析方法，可以将神经信息处理的抗扰机制转化到电子系统的电磁防护设计。

[1] ALDO A F, LUC P J S, DANIEL M W. Noise in the Nervous System[J]. Nat Rev Neurosci, 2008, 9(4): 292— 303.

[2] WHITE J A, RUBINSTEIN J T, KAY A R. Channel Noise in Neurons[J]. Trends Neurosci, 2000, 23: 131—137.

[3] LINDNER B, GARCIA-OJALVO J, NEIMAN A, et al. Effects of Noise in Excitable Systems[J]. Physics Reports, 2004, 392: 321—424.

[4] NICHOLLS J G. From Neuron to Brain[M]. Fifth Edition. Beijing: Science Press, 2014.

[5] GIMSEONG K, DARA K, HEARY E H, et al. Passive Sound-localization Ability of the Big Brown Bat (Eptes- icus Fuscus)[J]. Hearing Research, 1998, 119: 37—48.

[6] GONG Y, HAO Y, XIE Y, et al. Non-gaussian Noise Optimized Spiking Activity of Hodgkin-Huxley Neurons on Random Complex Networks[J]. Biophysical Chemistry, 2009, 14(4): 88—93.

[7] SAKUMURA Y, ISHII S. Stochastic Resonance with Differential Code in Feedforward Network with Intra-layer Random Connections[J]. Neural Networks, 2006, 19: 469—476.

[8] LIANG X, ZHAO L. Stochastic Resonance in Excitable Neuronal System with Phase-noise[J]. BICS, 2012, 7366: 304—310.

[9] 丁炯, 张宏, 童勤业. 蝙蝠听觉神经系统如何在复杂环境中识别昆虫[J]. 物理学报, 2012, 61(15): 1—11.

[10] CHEN L C, GU Y H. Coding Theories and Analyzing Methods of Information Contained in Neuronal Spike Trains[J]. Progress in Physiological Sciences, 1999, 30 (2): 101—106.

[11] BORST A, FREDERIC E. Theunissen. Information Theory and Neural Coding[J]. Nature Neuroscience, 1999, 2 (11): 947—957.

[12] LONDON M, ROTH A, BEEREN L, et al Sensitivity to Perturbations in Vivo Implies High Noise and Suggests Rate Coding in Cortex[J]. Nature, 2010, 466: 123—127.

[13] ABELES B D, WENG C, JIN J, et al. Temporal Precision in the Neural Code and the Timescales of Natural Vision [J]. Nature, 2007, 449: 92—95.

[14] REINAGEL P, REID R C. Temporal Coding of Visual Information in the Thalamus[J]. The Journal of Neuroscience, 2000, 20(14): 5392—5400.

[15] HUXTER J, BURGESS N, O′KEEFE J. Independent Rate and Temporal Coding in Hippocampal Pyramidal Cells[J]. Nature, 2003, 425(6960): 828—832.

[16] 唐孝威, 郭爱克, 吴思, 等. 神经信息学与计算神经科学[M]. 杭州: 浙江科学技术出版社, 2012.

[17] HODGKIN A L, HUXLEY A F. Currents Carried by Sodium and Potassium Ions Through the Membrane of the Giant Axon of Lolgio[J]. J Pjysiol, 1952, 116: 449—472.

[18] HODGKIN A L, HUXLEY A F. The Components of Membrane Conductance in the Giant Axon of Lolgio[J]. J Pjysiol, 1952, 116: 473—496.

[19] HODGKIN A L, HUXLEY A F. The Dual Effect of Membrane Potential on Sodium Conductance in the Giant Axon of Lolgio[J]. J Pjysiol, 1952, 116: 497—506.

[20] HODGKIN A L, HUXLEY A F. Quantitative Description of Membrane and its Application to Conduction and Excitation in Nevre[J]. J Pjysiol, 1952, 117: 500—544.

[21] 丁炯. 基于符号动力学的神经编码机制研究[D]. 杭州:浙江大学, 2014.

[22] 常小龙, 刘尚合, 满梦华, 等. 静电放电损伤自修复数字电路模型的建立与优化[J]. 高电压技术, 2012, 38(9): 2329—2335.

[23] MAN Meng-hua, LIU Shang-he, CHANG Xiao-long, et al. The Biological Property of Synthetic Evolved Digital Circuits with ESD Immunity-redundancy or Degeneracy [J]. Journal of Bionics Engineering, 2013, 10(3): 396— 403.

[24] 满梦华, 巨政权, 原青云, 等. 基于电磁仿生概念的静电放电注入损伤防护模型设计[J]. 高电压技术, 2011, 37(2): 375—381.

Study on Electromagnetic Protection Bionics by Mimicking the Anti-interference Mechanism of Neural network

MAN Meng-hua1, CAI Na2, MA Gui-lei1, WANG Zhen3

(1.Electrostatic & Electromagnetic Protection Institute, Ordnance Engineering College, Shijiazhuang 050003, China; 2.Ordnance Technical Research Institute, Shijiazhuang 050000, China; 3.Langfang Institute of Health Education, Langfang 065000, China)

Objective To study the good anti-interference ability of neural system of organism appears during information process, which can bring enlightenment to the study of bio-inspired electromagnetic protection. Methods We study the underlying mechanism of neural information processing in noise by using the modified bursting Hodgkin-Huxley neuron model to construct simulation models of neural system and S-space coding theory to analyzing neural information. The neural simulation model with different noise intensity is built, the neural information is coded by S-space coding theory, and influence of noise on neural coding is discussed. Results The results show that the neural information is encoded to symbol sequences in S-space and the frequency of input signal has monotonic relationship with the symbol sequences. The input noise changes the symbols of the symbol sequences but does not change the monotonic relationship, that is, the input noise doesn’t influence the information processing in S-space. Conclusion S-space coding theory is an important mechanism for anti-interference ability of neural system, which is worth to draw lessons from by electronic system.

S-space coding theory; Hodgkin-Huxley model; noise; anti-inference

10.7643/ issn.1672-9242.2017.04.003

TJ01；Q811

A

1672-9242(2017)04-0009-07

2016-10-31；

2016-11-2

国家自然科学基金项目（51407194）

满梦华（1984—），男，河北人，博士，主要研究方向为电磁防护仿生。