大角度机动下带挠性附件航天器转动惯量在轨辨识
2017-10-13谭述君吴志刚
何 骁,谭述君,吴志刚,2
(1.大连理工大学航空航天学院,大连 116024;2.大连理工大学工业装备结构分析国家重点实验室,大连 116024)
大角度机动下带挠性附件航天器转动惯量在轨辨识
何 骁1,谭述君1,吴志刚1,2
(1.大连理工大学航空航天学院,大连 116024;2.大连理工大学工业装备结构分析国家重点实验室,大连 116024)
针对大角度机动情况下带挠性附件航天器转动惯量在轨辨识的问题,提出一种将转动惯量参数估计和挠性附件状态估计相结合的并发递推算法。该算法以大角度机动情况下带挠性附件航天器的非线性动力学模型为基础,分别利用广义卡尔曼滤波做挠性附件振动模态的状态估计,最小二乘法做转动惯量的参数估计。最后通过并发递推算法将二者结合,完成了带挠性附件航天器的转动惯量参数辨识。为了提高算法的效率,采用一步最小二乘、多步广义卡尔曼滤波并发递推的算法。仿真结果表明,该辨识方法兼具高精度、高效率,并且算法有一定的抗干扰能力。
挠性附件;转动惯量;在轨参数辨识;广义卡尔曼滤波;最小二乘
0 引 言
随着航天技术的发展,许多大型航天器需要在轨展开和改变形状,地面测量的质量特性参数很难真实地反映航天器在轨运行时的情况,因此需要在轨辨识。另外,航天材料向着轻质化、柔性化方向发展,航天器挠性附件振动对其质量特性参数辨识的影响不可忽略[1]。由于航天器的任务越来越复杂,存在大角度机动的工况,动力学模型需要考虑非线性项的影响。因此,研究大角度机动下带挠性附件航天器转动惯量在轨辨识具有很重要的价值。
目前,国内外学者针对航天器转动惯量辨识问题的研究工作主要集中在刚体航天器方面。Bergman等[2]和Bergman等[3]提出一种高斯二阶滤波辨识卫星质量特性参数的方法,通过在常规卡尔曼滤波算法的基础上加入泰勒展开多项式二阶项,以提高滤波精度。Tanygin等[4]采用最小二乘算法来辨识自旋稳定卫星的质量特性参数,包括转动惯量和质心位置等参数。Wilson等[5-6]以SPHERE试验卫星为背景提出一种多变量并发递推最小二乘法在线辨识卫星的转动惯量、质心位置、总质量等质量特性参数。在国内,王书廷等[7]将质心位置和惯量矩阵的辨识问题解耦为两个最小二乘问题,提出一种递推最小二乘法在线辨识卫星的转动惯量和质心位置等参数。黄河等[8]针对小卫星转动惯量辨识提出了一种基于最小二乘的闭环辨识方法,在航天器完成姿态机动任务的同时,能够快速辨识出航天器的转动惯量。许莹等[9]研究带太阳电池阵的卫星惯量辨识方法,在建立带约束条件的优化辨识模型的基础上,基于约束最小二乘算法精确求解本体惯量和太阳电池阵惯量在内的12个变量值。徐文福等[10]提出了基于参数解耦的最小二乘法和基于PSO的非线性优化两种方法,辨识航天器的转动惯量、质量和质心位置。然而这些研究成果均将航天器视为刚体,没有考虑航天器挠性附件振动对航天器质量特性参数尤其是转动惯量在轨辨识的影响。近年来已有学者开展带挠性附件航天器转动惯量在轨辨识方面的工作。兰聪超等[11]针对小角度机动情况下带挠性附件卫星质量特性参数在轨辨识方法的问题,利用最小二乘与卡尔曼滤波并发递推的算法,辨识了带挠性附件卫星的转动惯量。朱东方等[12]针对复杂航天器的质量特性辨识问题,提出了基于扩展卡尔曼滤波的一种复杂航天器转动惯量矩阵的辨识方法。但现有的针对带挠性附件航天器的辨识算法对大角度机动工况下转动惯量参数辨识精度较差,且收敛速度很慢,需进一步研究高精度、高效率的辨识方法。
针对以上问题以及工程发展的需求,本文以典型的航天器——带挠性附件的卫星作为研究对象,控制力矩为输入信号,陀螺仪测量的姿态角速度等为输出信号,针对大角度机动情况,结合最小二乘法和广义卡尔曼滤波算法,提出了一种可在轨辨识带挠性附件航天器转动惯量参数的并发递推算法。
1 动力学模型
当卫星姿态角变化时,带挠性附件卫星姿态动力学方程和挠性附件振动方程[13-15]为
(1)
(2)


2 带挠性附件卫星转动惯量参数在轨辨识的并发递推算法

2.1转动惯量参数的估计
将待辨识的转动惯量参数表示成标称值和残差值相加的形式,
Jsat=Jnom+ΔJ
(3)
将式(3)代入式(1),得到
(4)
式(4)等号左边的处理为
(5)
(6)
式中:

基于式(5)和式(6)的描述形式,式(4)可以表示为
AJxJ=bJ
(7)
式中:


2.2挠性附件振动模态的估计
在带挠性附件卫星转动惯量的最小二乘描述形式中,当挠性附件振动模态已知时才可利用最小二乘法对卫星转动惯量参数进行辨识。目前,针对航天器挠性模态参数辨识的工作很多,经典的如文献[16-17]。对于挠性附件振动模态,本文将利用广义卡尔曼滤波算法来估计辨识。
2.2.1 广义卡尔曼滤波

非线性离散系统模型为
x(k+1)=f(x(k),k)+Γ(k)w(k)
(8)
y(k)=h(x(k),k)+v(k)
(9)
其中,测量噪声v(k)和过程噪声w(k)为互不相关的零均值白噪声。测量噪声和过程噪声的方差矩阵分别为R和Q,且满足
(10)
对上述这类非线性问题,可以通过局部线性化将卡尔曼滤波推广到非线性系统[18],得到广义卡尔曼滤波的递推方程如下,

(11)
P(k+ 1|k) =Φ(k+ 1|k)P(k)ΦT(k+ 1 |k) +Q
(12)
K(k+1)=P(k+1|k)HT(k+1)·
[H(k+1)P(k+1|k)HT(k+1)+R]-1
(13)


(14)
P(k+ 1) = [I-K(k+ 1)H(k+ 1)]P(k+ 1|k)
(15)
其中,状态转移矩阵Φ(k+1|k)和观测矩阵H(k+1)分别是f和h的雅可比矩阵。滤波初值和滤波方差矩阵的初值分别为x(0)=E[x(0)],P(0)=var[x(0)]。
2.2.2 系统状态的广义卡尔曼滤波描述形式
将带挠性附件卫星动力学方程式(1)和(2)转化为一阶微分方程的形式
(16)
式中:
设Aa(Jsat,xa)=D-1Axa,Ba(Jsat)=D-1B,式(16)可以表示为
(17)
引入观测方程
ya=Caxa
(18)
其中,观测值为姿态角和姿态角速度,即
采用差分近似将方程(17)离散化,差分的时间间隔为Ts

(19)
整理,得
x(k+1)= (TsAa(Jsat(k),x(k))+x(k))+
TsBa(Jsat(k))u(k)
(20)
同样,观测方程离散为
y(k)=Cax(k)
(21)
将式(20)和(21)与前面非线性离散系统模型的一般描述式(8)、(9)对比,有
f(x(k),k)= (TsAa(Jsat(k),x(k))+x(k))+
TsBa(Jsat(k))u(k)
(22)
h(x(k),k)=Cax(k)
(23)
将式(20)和式(21)代入广义卡尔曼滤波递推式(11)~(15)可实现状态量的估计,其中线性化矩阵Φ(k+1|k)和H(k+1)如下所示

(24)
其中,
(25)
H(k+1)=Ca
(26)

2.3并发递推算法

因为采用差分近似离散,对系统模型存在一定的近似,为了提高精度,广义卡尔曼滤波估计的采样周期应该尽量短。而最小二乘法做参数估计没有近似,较长的采样周期也能得到很好的辨识结果。综合以上两点,在保证算法精度的前提下,为了提高效率,本文采用q步广义卡尔曼滤波与1步最小二乘并发递推。其算法的具体流程如图1所示。先用广义卡尔曼滤波进行振动模态状态估计q次,体现为图1中内环;再用最小二乘法进行转动惯量参数的辨识,体现为图1中外环。反复迭代递推,即可得到转动惯量的辨识值。

图1 辨识算法的流程图Fig.1 Flow chart of the identification algorithm
3 仿真校验
3.1算例模型
仿真算例选取某型号通信卫星模型,如图2所示。卫星主要的挠性附件为对称的两个太阳能帆板,每个太阳能帆板长8.1 m,质量36.6 kg,卫星展开总跨度18.4 m,总质量2850.8 kg。该卫星是典型的带有挠性附件的航天器。该卫星模型的动力学分析表明,附件振动对整星动力学特性的影响主要由左右两侧帆板的第一阶振动模态决定,因此本文算例中只考虑第一阶模态的影响,忽略高阶模态。左右两侧帆板的一阶模态频率均为1.2754 Hz,模态阻尼比为0.005,转动惯量真实值Jreal和帆板转动刚柔耦合系数矩阵Prot为

图2 含有两个太阳帆板的带挠性附件卫星Fig.2 A satellite with two flexible solar panels
在数值仿真中,姿态角、角速度的初始值为φ0=[0,0,0]T,ω0=[0,0,0]T。仿真的输入力矩取为方波力矩信号,如图3所示,仿真时长为100 s。在实际工程中,考虑对姿态角速度的测量误差一般随着角速度的增大而增大,因此在该数值仿真中,姿态角速度响应在2°/s以内,图4为姿态角和姿态角速度响应曲线。

图3 输入力矩Fig.3 Input torque
3.2算法有效性校验
为了校验本文提出的广义卡尔曼滤波与最小二乘并发递推算法(EKL算法)的有效性,仿真算例还给出了不考虑非线性项的卡尔曼滤波与最小二乘并发递推算法(KL算法)的辨识结果作为对比。
采用本文提出的q步广义卡尔曼滤波与1步最小二乘相结合的并发递推算法,其中q等于100,采样间隔Ts为0.001 s。由于并发递推算法中用到的姿态角加速度不能通过直接测量得到,本文在算法中利用测量的姿态角速度进行差分近似计算得到。递推算法的初始值Jnom取为
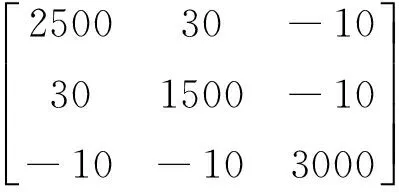

图4 力矩为M时的姿态角与角速度曲线Fig.4 The curve of attitude angle and angular velocity when the torque is M
当输入力矩较小时(0.1M),即卫星做小角度机动时,分别采用KL与EKL辨识算法进行转动惯量辨识,得到的辨识结果如图5所示。可以看出,两种算法都得到了正确的辨识结果,这是因为当卫星做小角度机动时,卫星的角速度非常小,可做近似忽略,这也验证了小角度机动时带挠性附件卫星转动惯量辨识算法忽略非线性项的合理性。当输入力矩为M时,采用KL与EKL辨识算法得到的转动惯量辨识结果如图6所示。可以看出,当卫星做大角度机动时,KL算法对主惯量辨识结果较好,但对惯性积的辨识结果则很差,甚至得不到收敛的结果。而本文提出的EKL递推算法可辨识出转动惯量参数,且精度较高。

图5 输入力矩为0.1M时的辨识结果Fig.5 Identification results when the input torque is 0.1M
表1给出了输入力矩为M时,分别采用KL和EKL算法得到的转动惯量辨识结果。可以看出,无论是什么情况,本文提出的EKL算法对主惯量辨识结果的相对误差在1%以内,惯性积相对误差在10%以内。综合上述对比分析表明,无论卫星做小角度机动,还是大角度机动,本文的EKL并发递推算法都能高效、准确地获得辨识结果,而KL算法由于忽略姿态角速度的非线性项影响,在大角度机动时已不能得到正确的辨识结果。因此,当卫星做大角度机动时,应该考虑非线性项的影响,而本文提出的多步广义卡尔曼滤波和最小二乘法相结合的并发递推算法则是处理带挠性附件卫星做大角度机动转动惯量参数辨识的有效方法。

图6 输入力矩为M的辨识结果Fig.6 Identification results when the input torque is M

辨识参数JxJyJzJxyJxzJyz真实值3035.43691800.28923934.274449.017-23.46-27.892KL方法辨识结果2993.981780.893740.0448.80-160.91-49.97相对误差1.37%1.08%4.94%0.43%585.89%79.17%EKL方法辨识结果3030.621784.453929.2945.46-21.50-30.24相对误差0.16%0.88%0.13%7.26%8.37%8.43%
3.3算法抗干扰性校验
上面的仿真算例中,由于只是对算法的有效性进行校验,并没有考虑噪声干扰对算法的影响,而在实际情况中不可能没有干扰,下面对并发递推算法的抗干扰能力进行研究。在其他条件都相同的情况下,在测量的姿态角、角速度的信号中加入信噪比(Signal to noise ratio, SNR)为140 dB的高斯白噪声。信噪比是指系统中信号与噪声的比例,计量单位为dB。在实际工程中,输入力矩的测量也会存在一定的误差,在仿真中考虑10%的误差,所以在输入力矩中加入信噪比30 dB的噪声。
图7给出了考虑噪声干扰情况下当输入力矩为M时的转动惯量辨识结果。与图6的结果相比,由于考虑了噪声干扰,辨识值收敛速度较慢,精度有所降低,但还是能获得收敛的结果。这说明本文提出的并发递推算法具有一定的抗干扰能力,而当测量信号的噪声继续增加时,则会进一步影响到辨识结果的精度与收敛速度。这就对辨识过程中用到的测量仪器的精度提出了一定的要求。

图7 考虑噪声的结果图Fig.7 Identification results in consideration of noise
4 结 论
本文针对大角度机动情况下带挠性附件航天器转动惯量参数辨识的问题,以带挠性附件卫星的动力学模型为基础导出了转动惯量参数的最小二乘辨识和挠性附件振动模态状态估计相结合的并发递推算法。本文考虑了姿态方程中的非线性项,得到了解决带挠性附件航天器转动惯量参数辨识问题更通用的方法。为了提高递推算法的精度和效率,本文采用了多步广义卡尔曼滤波与一步最小二乘法并发递推的算法。该算法只需要借助卫星原有的测量装置和执行机构,不需要额外的设备,工程可行性强。仿真算例的结果表明:在大角度机动的情况下,忽略动力学方程中非线性项的影响会减低辨识精度、甚至得到错误的辨识结果。而本文提出的多步广义卡尔曼滤波与一步最小二乘法的并发递推算法则可以实现带挠性附件航天器转动惯量参数的高精度、高效率辨识。
[1] 倪智宇, 邬树楠, 吴志刚, 等. 利用改进 TW-API 方法在轨辨识挠性航天器时变模态参数[J]. 宇航学报, 2015, 36(7): 769-776. [Ni Zhi-yu, Wu Shu-nan, Wu Zhi-gang, et al. On-orbit identification of time-varying modal parameters of flexible spacecraft by an improved TW-API method [J]. Journal of Astronautics, 2015, 36(7): 769-776.]
[2] Bergmann E, Dzielski J. Spacecraft mass property identification with torque-generating control[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(1): 99-103.
[3] Bergmann E V, Walker B K, Levy D R. Mass property estimation for control of asymmetrical satellites[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(5): 483-491.
[4] Tanygin S, Williams T. Mass property estimation using coasting maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 625-632.
[5] Wilson E, Sutter D W, Mah R W. MCRLS for on-line spacecraft mass-and thruster-property identification[J]. Parameters, 2004, 446(155): 324.
[6] Wilson E, Sutter D W, Mah R W. Multiple concurrent recursive least squares identification [C]. Proc IASTED International Conference on Intelligent Systems and Control, Honolulu,USA,August 23-25,2004.
[7] 王书廷, 曹喜滨. 卫星质量特性的在线辨识算法研究[C]. 第25届中国控制会议论文集, 哈尔滨, 中国, 2006年8月7-11日. [Wang Shu-ting, Cao Xi-bin. On-line mass-property identifica-tion algorithm research for satellite [C]. The 25th Chinese Control Conference, Harbin, China, August 7-11, 2006.]
[8] 黄河, 周军, 刘莹莹. 航天器转动惯量在线辨识[J]. 系统仿真学报, 2010,22(5): 1117-1120. [Huang He, Zhou Jun, Liu Ying-ying. On-line identification of spacecraft moment of inertia [J]. Journal of System Simulation, 2010, 22(5): 1117-1120.]
[9] 许莹, 吕旺, 李云端, 等. 多刚体卫星转动惯量在轨辨识[J]. 空间控制技术与应用, 2015, 41(6): 31-36. [Xu Ying, Lv Wang, Li Yun-duan, et al. Identification of rotary inertia for multi-body satellite [J]. Aerospace Control and Application, 2015, 41(6): 31-36.]
[10] 徐文福, 何勇, 王学谦, 等. 航天器质量特性参数的在轨辨识方法[J]. 宇航学报, 2010,31(8): 1906-1914. [Xu Wen-fu, He yong, Wang Xue-qian, et al. On orbit identification of mass characteristic parameters for spacecraft [J]. Journal of Astronautics, 2010, 31(8): 1906-1914.]
[11] 兰聪超, 谭述君, 吴志刚, 等. 带挠性附件卫星转动惯量的在轨辨识[J]. 振动与冲击, 2017, 36(8): 16-21.[Lan Cong-chao, Tan Shu-jun, Wu Zhi-gang, et al. On-orbit identification of moments of inertia for satellites with flexible appendages [J]. Journal of Vibration and Shock, 2017, 36(8): 16-21.]
[12] 朱东方, 王卫华, 宋婷, 等. 复杂挠性航天器转动惯量在线辨识算法研究[J]. 上海航天, 2015, 32(5): 1-8, 14.[Zhu Dong-fang, Wang Wei-hua, Song Ting, et al. On-line identification of flexible spacecraft moment of inertia[J]. Aeros-pace Shanghai, 2015, 32(5):1-8,14.]
[13] 游斌弟, 温建民, 张广玉, 等. 航天器薄壳柔性附件展开耦合行为特性研究[J]. 宇航学报, 2015, 36(6): 640-647. [You Bin-di, Wen Jian-min, Zhang Guang-yu, et al. Study on coupling behavior of spacecraft deployment with flexible appendages of shell structure [J]. Journal of Astronautics, 2015, 36(6): 640-647.]
[14] 吕旺, 向明江, 叶文郁, 等. 挠性卫星在轨非约束模态计算研究[J]. 宇航学报, 2014, 35(4): 404-409. [Lv Wang, Xiang Ming-jiang, Ye Wen-yu, et al. Research on calculation of on-orbit unconstrained modal of flexible satellite [J]. Journal of Astronautics, 2014, 35(4): 404-409.]
[15] 张嘉钟, 魏英杰, 曹伟. 飞行器动力学与控制[M]. 哈尔滨:哈尔滨工业大学出版社, 2011.
[16] Adachi S, Yamaguchi I, Kida T, et al. On-orbit system identification experiments on engineering test satellite-VI[J]. Control Engineering Practice, 1999, 7(7): 831-841.
[17] Juang J N. An eigensystem realization algorithm using data correlations (ERA/DC) for modal parameter identification[J]. Journal of Control Theory and Advanced Technology, 1988, 4(1): 5.
[18] 蔡金狮. 飞行器气动参数辨识学[M]. 北京:国防工业出版社, 2003.
On-OrbitIdentificationoftheMomentofInertiaforaSpacecraftwithFlexibleAppendagesduringaLarge-AngleManeuver
HE Xiao1, TAN Shu-jun1, WU Zhi-gang1,2
(1. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024,China;2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024,China)
For the problem of the on-orbit identification of the moment of inertia for a spacecraft with flexible appendages during a large-angle maneuver, a concurrent recursive algorithm is proposed in this paper, which combines the estimation of the inertia parameters with the state estimation of the flexible appendages’ vibration modes. The algorithm is based on the nonlinear dynamic model of a spacecraft with flexible appendages during a large-angle maneuver. The extended Kalman filter is used to estimate the states of the flexible appendages’ vibration modes, and the least square method is used to estimate the parameters of the moment of inertia. Finally, the inertia parameters of the spacecraft are obtained by the concurrent recursive algorithm. In order to improve the efficiency of the algorithm, a recursive algorithm based on one-step least square method and multi-step extended Kalman filter is proposed. Simulation results show that the proposed algorithm not only improves the computational accuracy and efficiency, but also has the capability of anti-interference.
Flexible appendages;Moment of inertia;On-orbit parameter identification;Extended Kalman filter (EKF);Least square
V557+.1
A
1000 -1328(2017)09- 0927- 09
10.3873/j.issn.1000-1328.2017.09.005
2017- 01-19;
2017- 06-22
国家自然科学基金(11572069,11502040,11432010);中央高校基本科研业务费专项资金(DUT16ZD225)
何骁(1992-),男,硕士生,主要从事飞行器动力学系统辨识研究。
通信地址:辽宁省大连理工大学综合1号实验楼406(116023)
电话:(0411)84706213
E-mail: jsychx@mail.dlut.edu.cn
谭述君(1979-),男,博士,副教授,主要从事航天器动力学与控制、在轨参数辨识、保结构数值方法、鲁棒与最优控制研究。本文通信作者。
通信地址:辽宁省大连理工大学综合1号实验楼409A(116023)
电话:(0411)84706213
E-mail: tansj@dlut.edu.cn
