逆瑞利分布的有效估计
2017-10-12卢建萍史洁茹郝博
卢建萍, 史洁茹,郝博
(1.山西师范大学数学与计算机科学学院, 山西 临汾 041000;2.四川大学数学学院,四川 成都 610065)
逆瑞利分布的有效估计
卢建萍1, 史洁茹2,郝博1*
(1.山西师范大学数学与计算机科学学院, 山西 临汾 041000;2.四川大学数学学院,四川 成都 610065)
推导逆瑞利分布的密度函数和分布函数的MLE和UMVUE, 并给出估计量r阶矩的精确表达式。对估计量的均方误差和变异系数做渐进展开, 在大样本下给出逆瑞利分布有效估计的判断条件。
逆瑞利分布; 密度函数; 分布函数;MLE; UMVUE
Abstract∶The MLE and UMVUE of the density function and distribution function were derived for the inverse Rayleigh distribution, and the explicit expressions of the r-th moment of these estimators were given. The mean square error and variation coefficient of the estimators were asymptotically expanded. Finally, the judgement for the effective estimation of the inverse Rayleigh distribution was given in the large sample.
Key words∶inverse Rayleigh distribution; density function; distribution function; MLE; UMVUE
逆瑞利分布[1-2]和指数分布[3]、瑞利分布[4]等类似, 都是寿命测试中的重要分布。 设随机变量X服从参数为θ的逆瑞利分布,则其分布函数和密度函数分别为
F(x)=exp(-θx-2),
f(x)=2θx-3exp(-θx-2),
其中x>0,θ>0。 目前, 对逆瑞利分布研究主要集中在未知参数θ和可靠性函数G(x)=1-F(x) 的估计问题。 但在对可靠性研究中, 较少有文献给出估计量r阶矩的精确表达式,对分布函数和密度函数的估计研究具有重要的理论和应用价值[5-7]。 本文首先给出逆瑞利分布分布函数和密度函数的极大似然估计(maximum likelihood estimation,MLE)和一致最小方差无偏估计(uniform minimum variance unbiased estimator, UMVUE), 再推导估计量r阶矩的精确表达式, 进而推导估计量均方误差和变异系数的渐进表达式, 最后比较两种估计量的优劣性。
1 MLE和UMVUE
定理1 设随机变量序列{Xi},i=1,…,n服从参数为θ的逆瑞利分布, 则其分布函数F(x)的MLE和UMVUE分别为:

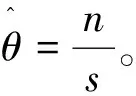
证毕。
类似可推出定理2。
定理2 设随机变量序列{Xi},i=1,…,n服从参数为θ的逆瑞利分布, 则其密度函数f(x)的MLE和UMVUE分别为

2 r阶矩
r阶矩作为分布的特征数,有着重要应用。 诸如数学期望、方差、均方误差、变异系数、偏度系数、峰度系数等, 皆与r阶矩有着直接关系。 故很有必要给出估计量r阶矩的精确表达式。
定理3 设θ,x>0且n>r≥1(n∈+), 则
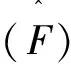
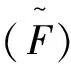
证明


U(a,b,c)=c1-bU(1+a-b,2-b,c)。
类似可推出定理4。
定理4 设θ,x>0且n>r≥1(n∈+), 则
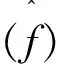
3 均方收敛性
引理1 对任意固定的y>0,a≥0, 若υ→+∞, 则
其中
a0(a,y)=1,a1(a,y)=y2/2-(a+1)y+(6a2+1)/12,
引理2 对任意固定的z>0,a>0, 若n→+∞, 则
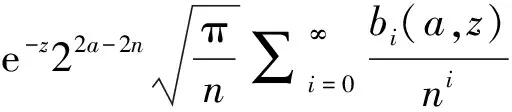
其中
b0(a,z)=1,b1(a,z)=z2+2(1-a)z+(8a2-20a+17)/8,
注1 引理1和引理2可由拉普拉斯定理[8]得到,证明略。
定理5 当n→∞时
(1)
(2)
其中,z=θx-2>0。
证明由均方误差定义可得

(3)
(4)
而由Stirling公式[9-10]得
(5)

把(3), (4), (5)代入均方误差表达式化简即得(1)。 (2)可类似证明。
定理6 当n→∞时
其中z=θx-2>0。
其证明过程与定理5的证明相似。
4 变异系数
下面给出另外一个衡量估计量优劣的指标——变异系数。 其证明过程与证明均方误差的过程极为相似, 此处仅给出结论。
定理7 当n→∞时
定理8 当n→∞时
5 有效估计
在大样本下, 从均方误差的角度考虑, 由定理5,6我们可以给出判断有效估计量的条件:
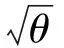
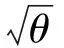
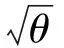
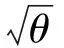
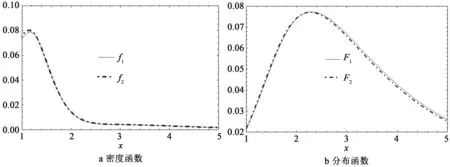
例1 设定参数θ=2.8,n=40 ,0 图1 密度函数和分布函数在不同估计下的均方误差比较Fig.1 The mean square error comparison of density function and distribution function under different Estimators 在大样本下, 从变异系数角度考虑, 由定理7,8我们同样可以给出估计量波动程度的条件: 在小样本下,虽然不能得到一些简单的条件去判断哪个估计优越,但是定理3和定理4中给出的r阶矩的表达式可以在常用的数学软件上直接计算,因此,计算估计量的均方误差和变异系数也不会有实质性的困难。 [1]FEROZE N, ASLAM M. On posterior analysis of inverse Rayleigh distribution under singly and doubly type II censored data[J]. International Journal of Probability and Statistics, 2012, 1(5): 145-152. [2]ROSAIAH K, KANTAM R R L. Acceptance sampling based on the inverse Rayleigh distribution[J]. Economic Quality Control, 2005, 20(2): 277-286. [3]BROWN M. Estimation of an exponential distribution[J]. Probability in the Engineering and Informational Sciences, 1997, 11(3): 341-359. [4]LIN J G. Parameter estimations of Rayleigh distribution[J]. Chinese Quart J Math, 2000, 15(4): 49-54. [5]PATIL G P,WANI J K. Minimum variance unbiased estimation of the distribution function admitting a suffcient statistic[J].Annals of the Institute of Statistical Mathematics, 1966, 18(1): 39-47. [6]SEHEULT A H,QUESENBERRY C P. On unbiased estimation of density functions[J]. The Annals of Mathematical Statistics, 1971 , 42(4): 1434-1438. [7]徐传胜. 圣彼得堡数学学派研究[M]. 北京: 科学出版社. 2016: 183-195. [8]成平,陈希孺,陈桂景,等. 参数估计[M]. 上海: 上海科学技术出版社. 1985: 88-95. [9]OLVER F W J, LOZIER D W, BOISVERT R F,et al. NIST handbook of mathematical functions[M]. New York,US : Cambridge University Press, 2010. [10]NEMES G. On the coeffcients of the asymptotic expansion of n![J]. Journal of Integer Sequences, 2010, 13(6):1-5. An efficient estimation of the inverse Rayleigh distribution LU Jian-ping1,SHI Jie-ru2, HAO Bo1* (1. School of Mathematics &Computer Science, Shanxi Normal University, Linfen 041000, China; 2. School of Mathematics, Sichuan University, Chengdu 610065, China) O212.1 A 1002-4026(2017)05-0086-05 10.3976/j.issn.1002-4026.2017.05.014 2016-06-20 山西省自然科学基金 (2013011002-1) 卢建萍(1986—), 女,硕士, 研究方向为统计推断、参数估计。 *通信作者,郝博。E-mail:fobfge@126.com