基于连续−离散介质耦合的密实充填开采地表沉陷预测模型

郭庆彪，郭广礼，吕鑫，张文馨，覃双煜



基于连续−离散介质耦合的密实充填开采地表沉陷预测模型

郭庆彪1, 2, 3，郭广礼1, 3，吕鑫2，张文馨1, 3，覃双煜1, 3

(1. 中国矿业大学环境与测绘学院，江苏徐州，221116；2. 滁州学院地理信息与旅游学院，安徽滁州，239000；3. 国土环境与灾害监测国家测绘地理信息局重点实验室，江苏徐州，221116)

为构建固体密实充填开采地表沉陷预测模型，首先结合现场钻孔窥视及相似材料模拟分析固体密实充填开采的覆岩变形特征；随后采用Winkler和Vlazov两类弹性地基梁建立基本顶力学模型，得到基本顶弯曲下沉方程；将基本顶的弯曲下沉视为上覆岩层沉降的边界条件，基于离散介质运移规律推导出固体密实充填开采的地表沉陷预测模型。最后将预测模型应用于花园煤矿，得到的下沉量预测值与实测值基本吻合，证实了模型的准确性。

固体密实充填开采；基本顶；弹性地基梁；地表沉陷预计

固体密实充填采煤技术是解决“三下”压煤的一种有效技术手段，现已成功应用于我国平顶山、新汶、淮北等多个矿区，为实现煤矿安全、绿色和高效开采提供了一种创新技术[1]。在固体密实充填开采中，充填体联合周边煤岩共同承担覆岩荷载，上覆岩层只发生缓慢下沉，由此衍生的地表沉降规律与垮落法明显不同。余伟健等[2]认为矸石充填采煤过程中，充填体、围岩和煤柱系统的协同作用可分为3个阶段：煤柱支撑阶段、充填体与煤柱支撑阶段及系统联合作用阶段。马文菁等[3]结合数值模拟实验结果分析得出密实充填开采时顶板的垂直应力与煤壁的水平应力比垮落法开采的明显要高，佐证了余伟健的上述结论。缪协兴 等[4−5]指出矸石充填综采的基本顶垮落步距增大，覆岩变形空间减小，基本顶及关键层一般不会失稳破断，可采用连续介质力学分析岩层移动。杨宝贵等[6]结合数值模拟实验，得出充填开采显著降低了地表的移动变形，地表趋近于均匀下沉和连续变形。瞿群迪等[7]认为充填开采的地表下沉主要由顶板移近量、欠接顶量和充填体压缩量3方面组成，提高充实率可减小地表下沉值。不难看出，研究者围绕着固体密实充填采煤的覆岩及地表移动变形规律已开展大量研究工作。在此基础上，建立充填采煤的岩层移动计算模型，预估充填采煤后的地表移动变形，将为支架选型、工作面布置及建(构)筑物的运营维护提供决策支持。缪协兴等[4]认为固体密实充填采煤的覆岩移动变形向上传递过程遵循等体积原则，基于连续介质力学推导出岩层移动的计算公式。李猛等[8]采用弹性地基薄板理论，推导了基本顶挠度、应力方程及其破断的临界条件。王磊[9]提出了固体密实充填采煤有结构关键层和无结构关键层控制的2种岩层移动模型。GUO 等[10]提出了基于等价采高的概率积分法预计模型。综上所述，针对固体密实充填采煤的覆岩及地表移动变形预测模型的研究可归分为2类：一类基于连续介质力学；另一类基于随机介质力学。前者涉及的参数较多，且难于获取，后者是一种极限思想，其合理性与科学性无从考究。为此，本文作者基于连续−离散介质耦合的基本思想，建立固体密实充填开采后的地表沉陷预测模型，为该领域的研究提供新思路。

1 固体密实充填开采覆岩变形特征

垮落法管理顶板时，煤层挖空使得上覆岩层失去支撑作用，顶板覆岩在其自重及上覆岩层荷载作用下，相继垮落、断裂和弯曲直至地表，最终在采区地表形成范围远大于采空区的下沉盆地。而在固体密实充填开采中，矸石等废弃固体废料充入采空区，经夯实机夯实后能够支撑上覆岩层，控制覆岩的移动变形，因此，其覆岩变形特征与垮落法不尽相同[11−12]。为揭示固体密实充填开采覆岩变形特征，结合智能电视原位实测与室内相似材料模拟试验进行研究。平顶山某矿钻孔窥视结果见图1，固体密实充填开采覆岩结构形态特征模拟结果见图2。充填体的相似材料选用海绵与泡沫的混合材料[13]。

(a) 1号钻孔拍摄结果；(b) 2号钻孔拍摄结果；(c) 3号钻孔拍摄结果；(d) 4号钻孔拍摄结果

(a) 邹城某矿(采厚3 m，埋深300 m)；(b) 阳泉某矿(采厚2.5 m，埋深160 m)；(c) 鄂尔多斯某矿(采厚2.5 m，埋深400 m)；(d) 济宁某矿(采厚3.0 m，埋深550 m)

由图1可知：在固体密实充填开采中，距离采空区较近的岩层发生了变形破坏，但仍能保持原始层位特征。岩层内未出现“垮落带”，仅形成一定高度的裂隙带，实测平均裂隙带高度约为6.8 m。

由图2可知：充填体填充于采空区，减少顶板的下沉空间，岩层移动变形过程中始终未出现离层现象。与此同时，由于充填体的侧向限压，保证了周边煤体的准三向受压条件，提高了煤体的稳固性。充填体联合周边煤体共同承担覆岩荷载，控制覆岩的移动变形，覆岩仅发育一定高度的断裂带，其形态主要以完整层状结构的弯曲带为主，在上部岩层荷载的作用下，直接顶内发育着竖向裂缝，而基本顶内仅产生连续的弯曲下沉。

2 固体密实充填开采基本顶力学分析

2.1 基本顶力学模型

在固体密实充填开采中，充填体与断裂的直接顶块体充填于采空区，连同周边煤体共同承担上覆岩层荷载，控制覆岩的移动变形，使得基本顶仅发生弯曲变形而不破断[8]。因此，可用连续介质力学模型分析基本顶的移动变形，将基本顶视为上部承受覆岩荷载，下部由弹性地基支撑的梁。而根据下部弹性地基的介质属性可将其分为2类：一类由矸石充填体和碎裂的直接块体组成，各块体间几乎无剪切作用，无法扩散应力和变形，此时可将其视为Winkler弹性地基；而另一类为采区周边煤体，矸石的充填使其保持三向受力状态，受采动影响较小，几乎无片帮现象，仍保持较好的介质属性，能够扩散应力和变形，可将其视为Vlazov弹性地基[14]。补充如下假设条件：

1) 基本顶上覆荷载简化为均布荷载0(其中，0=，为覆岩平均容重，为基本顶平均埋深)；

2) 不考虑岩梁本身的纵向变形，岩梁挠度与充填体、煤柱的压缩变形相等。

基本顶的受力简图如图3所示。

图3 基本顶岩梁受力分析

图3中，1为工作面面宽的一半，2可由下式计算得出：

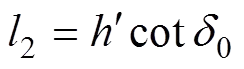
周大伟[16]经研究认为覆岩移动边界接近“S”型曲线而非直线，因此，覆岩移动边界角需在地表盆地边界角0基础上加以修正，得

2.2 基本顶弯曲变形

2.2.1 充填体−基本顶系统

根据Winkler弹性地基梁假说[17]，地基表面任一点的压力与该点位移成正比，即

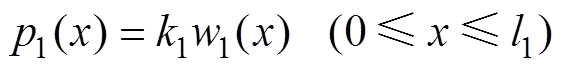
式中：1为地基系数，主要由充填体变形特性确定；1()为基本顶受到的地基支撑力；1()为基本顶的弯曲下沉挠度。由此可得充填体上方基本顶岩梁的挠曲微分方程为

(4)

式中：为弹性模量；为惯性矩；1为特征系数，可由下式计算得出：

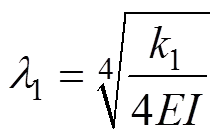
利用初参数法求解式(4)，得

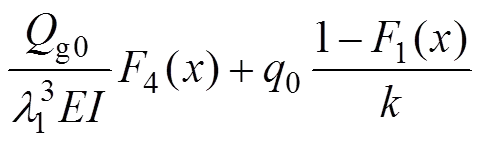
式中：g0，g0，g0和g0分别为基本顶端点(=0)的挠度、转角、弯矩和剪力。1()，2()，3()和4()的表达形式为

(7)

2.2.2 煤柱−基本顶系统

根据Vlazov弹性地基梁假说[17]，假设Winkler地基模型中各弹簧之间存在剪切作用，则外载荷与位移之间的关系为

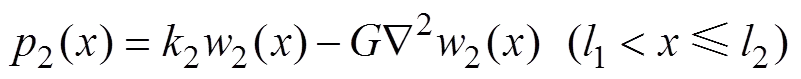
由此可得煤体上方基本顶岩梁的挠曲微分方程为

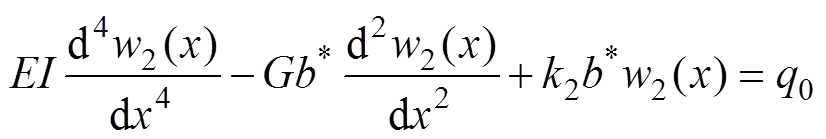
(9)

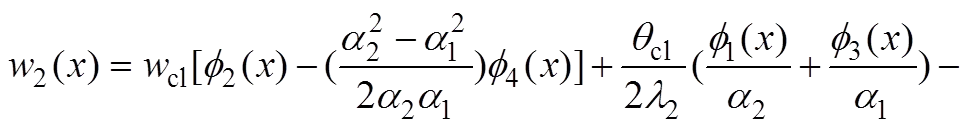
(10)

式中：cl，cl，cl和cl为基本顶在=1位置时的挠度、转角、弯矩和剪力；为积分变量；2，1，α，，，和的表达形式为

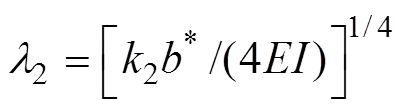
(11)

2.2.3 连续性及边界条件

补充下述连续性及边界条件以求解式(6)和式(10)中的初始参数。

基本顶(=0)处边界条件：

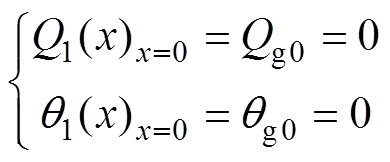
基本顶(=1)处的连续性条件：

(13)

基本顶(=2)处的连续性条件：

联合式(13)和式(14)可得

(15)

通过求解方程组(12)和(15)，可得初始参数g0，g0，g0，g0，cl，cl，cl和cl的解，进而得到基本顶弯曲下沉()的计算公式。由于初始参数的表达式过于复杂，本文不具体给出，在实际应用中，可借助MATLAB计算初始参数的数值解。

3 固体密实充填开采地表沉陷预测模型

岩层及地表移动变形规律与颗粒体介质模型所描述的规律宏观相似[18]。该模型认为岩体介质由类似于砂粒等的小岩块组成，颗粒间完全失去联系，其运动服从统计规律的随机过程。通过砂箱模型可证实单元开采引起地表下沉盆地的函数形式与正态分布概率密度函数相同，以此作为被积函数，以开采空间作为积分域，可推导出地表任意点的下沉[19]。而固体密实充填开采通过回填固体废料缩小了煤层的实际开采厚度，基于上述思想，GUO等[10]提出了适用于固体密实充填开采的基于等价采高的概率积分法预测模型：

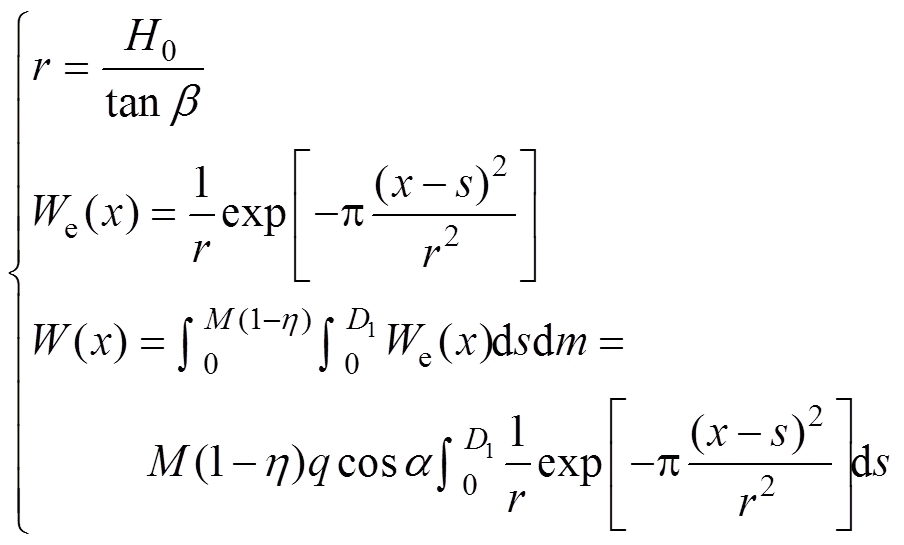
式中：为主要影响半径；为煤层倾角；tan为主要影响正切；0为平均埋深；e()为单元开采引起地表点(，)的下沉值；为开采单元横坐标；为下沉系数；1和2为工作面尺寸；为实际采高；为充实率。

该方法将采空区视为矩形区域，并假设地下开采空间高度处处相等，但大量生产实践和岩层移动研究表明上述假说不尽合理。除此之外，该方法通过引入“拐点偏移距0”，对煤壁处顶板的悬空效果进行简单的等效处理，而拐点偏移距选取的恰当与否直接影响着预计精度。同时，这割裂了地表下沉与地质采矿条件的函数关系，降低了预计的科学性和可信度[20]。为此，本文作者以基本顶为研究对象，重新定义固体密实充填开采的覆岩下沉空间：边界为基本顶的原始应力固定端，顶边为原岩基本顶位置，底边为弯曲下沉后的基本顶位置，三者围成的闭合区域作为覆岩下沉空间。考虑到固体密实充填开采时，基本顶上方覆岩紧密接触，层间无离层现象，开采沉陷在基本顶上方覆岩内按等体积原则向上传递[4]，可以忽略岩石的碎胀影响。鉴于采空区的对称性，得到固体密实充填开采地表沉陷预测模型：

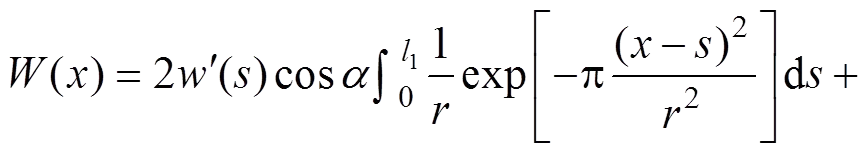
(17)

4 工程验证

本次试验地点为山东花园煤矿。该矿位于济宁市金乡县境内，北距济宁市区约48 km，南距商丘90 km。1316充填面位于井田东翼，属二叠系山西组，煤层平均采高为3.0 m，平均埋深为550 m，煤层平均倾角12°，工作面走向长度为220 m，倾向长度为100 m，总体呈近似东西走向的单斜构造。为揭示矸石密实充填开采后地表沉降特征，特在1316工作面上方布设1条观测线，如图4所示。

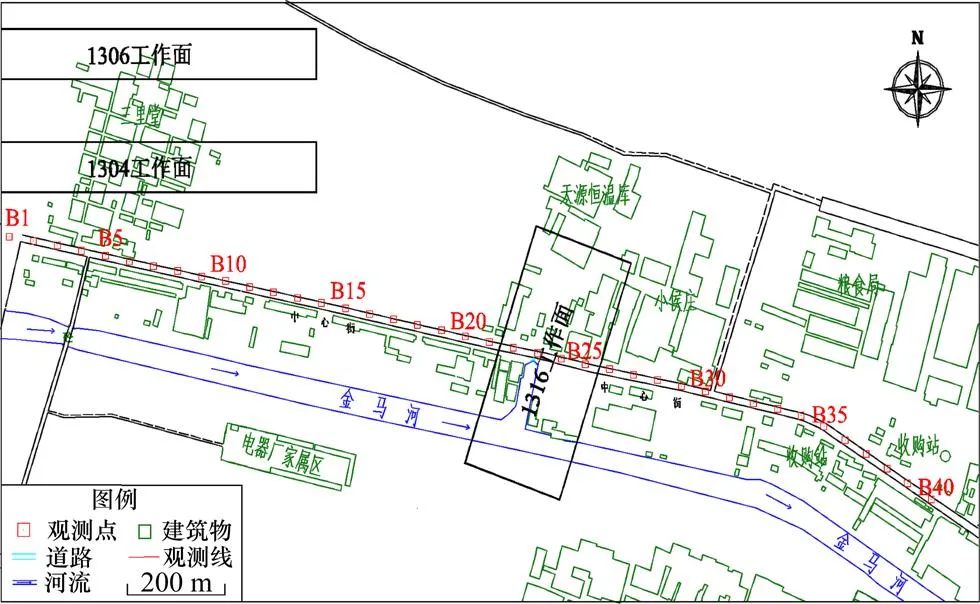
图4 1316工作面及地表观测线示意图

结合研究区的地质采矿条件，得到以下计算参数：1=50 m，0=52°，基本顶厚度0=20 m，基本顶弹性模量=5 GPa，充填体地基系数1=1×108N/m3，煤岩体地基系数2=1×109N/m3，煤岩剪切模量= 0.18 GPa，覆岩平均容重=27 kN/m3，基本顶平均埋深0=525 m。将上述参数代入预测模型，得到各点下沉量预测值与实测值对比结果，见图5。

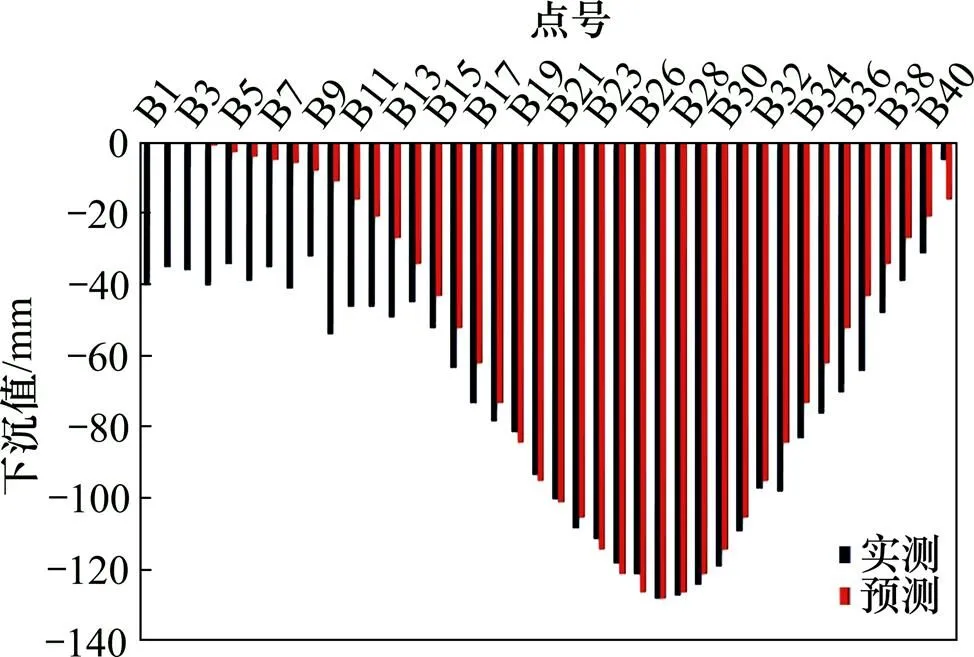
图5 下沉量预测值与实测值对比图

由图5可知：在测点B14~41区间，预测结果与实测数据基本吻合，平均预报误差均小于10 mm，且该方法能够维系地质采矿条件与地表下沉的完整函数关系，避免人为干预，提高预测结果可信度；而在测点B1~13区间，下沉量预测值与实测值相差较大，分析其原因，可能是观测线B1~13区间北侧毗邻1304和1306采空区，在老空区残余沉降的影响下，B1~13的下沉值增大，使得盆地无法收敛。

5 结论

1) 建立基本顶力学模型，并结合基本顶的边界条件及连续性条件得到了基本顶弯曲下沉方程。

2) 重新定义固体密实充填开采的覆岩下沉空间，将固体密实充填开采的基本顶弯曲下沉视为覆岩移动的边界条件，结合随机介质运移规律推导出固体密实充填开采的地表沉陷预测模型。将预测模型应用于山东花园煤矿，得到的下沉量预测值与实测值基本吻合，取得了较好的工程实践效果。

[1] 缪协兴, 张吉雄, 郭广礼. 综合机械化固体充填采煤方法与技术研究[J]. 煤炭学报, 2010, 35(1): 1−6. MIAO Xiexing, ZHANG Jixiong, GUO Guangli. Study on waste filling method and technology in fully mechanized coal mining[J]. Journal of China Coal Society, 2010, 35(1): 1−6.

[2] 余伟健, 冯涛, 王卫军, 等. 充填开采的协作支撑系统及其力学特征[J]. 岩石力学与工程学报, 2012, 31(S1): 2803−2813. YU Weijian, FENG Tao, WANG Weijun, et al. Coordination support systems in mining with filling and mechanical behavior[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 2803−2813.

[3] 马文菁. 矸石充填开采条件下岩层与地表移动变形规律研究[D]. 太原: 太原理工大学矿业工程学院, 2013: 24−42. MA Wenjing. The movement and deformation research about overburden and surface filled by coal gangue[D]. Taiyuan: Taiyuan University of Technology. College of Mining Engineering, 2013: 24−42.

[4] 缪协兴, 黄艳利, 巨峰, 等. 密实充填采煤的岩层移动理论研究[J]. 中国矿业大学学报, 2012, 41(6): 863−867. MIAO Xiexing, HUANG Yanli, JU Feng, et al. Strata movement theory of dense backfill mining[J]. Journal of China University of Mining & Technology, 2012, 41(6): 863−867.

[5] 张吉雄, 李剑, 安泰龙, 等. 矸石充填综采覆岩关键层变形特征研究[J]. 煤炭学报, 2010, 35(3): 357−362. ZHANG Jixiong, LI Jian, AN Tailong, et al. Deformation characteristic of key stratum overburden by raw waste backfilling with fully-mechanized coal mining technology[J]. Journal of China Coal Society, 2010, 35(3): 357−362.

[6] 杨宝贵, 彭杨皓, 李杨, 等. 充填开采地表移动变形规律数值模拟分析[J]. 金属矿山, 2014(12): 169−174. YANG Baogui, PENG Yanghao, LI Yang, et al. Numerical simulation analysis of ground movement deformation law in backfilling mining[J]. Metal Mine, 2014(12): 169−174.

[7] 瞿群迪, 姚强岭, 李学华, 等. 充填开采控制地表沉陷的关键因素分析[J]. 采矿与安全工程学报, 2010, 27(4): 458−462. QU Qundi, YAO Qiangling, LI Xuehua, et al. Key factors affecting control surface subsidence in backfilling mining[J]. Journal of Mining & Safety Engineering, 2010, 27(4): 458−462.

[8] 李猛, 张吉雄, 姜海强, 等. 固体密实充填采煤覆岩移动弹性地基薄板模型[J]. 煤炭学报, 2014, 39(12): 2369−2373. LI Meng, ZHANG Jixiong, JIANG Haiqiang, et al. A thin plate on elastic foundation model of overlying strata for dense solid backfilling mining[J]. Journal of China Coal Society, 2014, 39(12): 2369−2373.

[9] 王磊. 固体密实充填开采岩层移动机理及变形预测研究[D]. 徐州: 中国矿业大学环境与测绘学院, 2012: 105−148. WANG Lei. Study on strata movement mechanism and deformation prediction of coal mining with solid waste compacted filling[D]. Xuzhou: China University of Mining and Technology. School of Environment Science and Spatial Informatics, 2012: 105−148.

[10] GUO Guangli, ZHU Xiaojun, ZHA Jianfeng, et al. Subsidence prediction method based on equivalent mining height theory for solid backfilling mining[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(10): 3302−3308.

[11] 王磊, 张鲜妮, 郭广礼, 等. 固体密实充填开采地表沉陷预计模型研究[J]. 岩土力学, 2014, 35(7): 1973−1978. WANG Lei, ZHANG Xianni, GUO Guangli, et al. Research on surface subsidence prediction model of coal mining with solid compacted backfilling[J]. Rock and Soil Mechanics, 2014, 35(7): 1973−1978.

[12] 缪协兴, 张吉雄, 郭广礼. 综合机械化固体废物充填采煤方法与技术[M]. 徐州: 中国矿业大学出版社, 2010: 1−30. MIAO Xiexing, ZHANG Jixiong, GUO Guangli. Method and technology of fully-mechanized coal mining with solid waste filling[M]. Xuzhou: China University of Mining and Technology Press, 2010: 1−30.

[13] 彭科翔. 固体充填开采地表移动规律研究[D]. 徐州: 中国矿业大学环境与测绘学院, 2014: 28−58. PENG Kexiang. Study on surface deformation and movement laws in the solid backfill mining[D]. Xuzhou: China University of Mining and Technology. School of Environment Science and Spatial Informatics, 2014: 28−58.

[14] 黄义, 何芳社. 弹性地基上的梁、板、壳[M]. 北京: 科学出版社, 2005: 26−45. HUANG Yi, HE Fangshe. Beam, plate and shell structures on the elastic foundation[M]. Beijing: Science Press, 2005: 26−45.

[15] 煤炭工业局. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M]. 北京: 煤炭工业出版社, 2000: 117−224. Coal Industry Bureau. Buildings, water bodies and railways and the main shaft and this coal pillar and press coal mining regulations[M]. Beijing: China Coal Industry Publishing House, 2000: 117−224.

[16] 周大伟. 煤矿开采沉陷中岩土体的协同机理及预测[D]. 徐州: 中国矿业大学环境与测绘学院, 2014: 41−59. ZHOU Dawei. The synergy mechanism between rock mass and soil in mining subsidence and its prediction[D]. Xuzhou: China University of Mining and Technology. School of Environment Science and Spatial Informatics, 2014: 41−59.

[17] 龙驭球. 弹性地基梁的计算[M]. 北京: 人民教育出版社, 1982: 6−27. LONG Yuqiu. Calculation of the beam on elastic foundation[M]. Beijing: People’s Education Press, 1982: 6−27.

[18] 刘宝琛, 廖国华. 煤矿地表移动的基本规律[M]. 北京: 中国工业出版社, 1965: 19−29.LIU Baochen, Liao Guohua. Basic law of surface movement and deformation of coal mining[M]. Beijing: China Industry Press, 1965: 19−29.

[19] 李培现, 谭志祥, 闫丽丽, 等. 基于支持向量机的概率积分法参数计算方法[J]. 煤炭学报, 2010, 35(8): 1247−1251. LI Peixian, TAN Zhixiang, YAN Lili, et al. Calculation method of probability integration method parameters based on support vector machine[J]. Journal of China Coal Society, 2010, 35(8): 1247−1251.

[20] 张兆江, 吴侃, 张安兵. 基于关键层理论的概率积分法开采沉陷预计[J]. 煤炭科技, 2010(1): 23−26.ZHANG Zhaojiang, WU Kan, ZHANG Anbing. Surface subsidence prediction based on the key strata theory[J]. Coal Science & Technology Magazine, 2010(1): 23−26.

(编辑 伍锦花)

Research on surface subsidence prediction of dense solid backfilling mining based on the coupling of continuous and discrete medium

GUO Qingbiao1, 2, 3, GUO Guangli1, 3, LÜ Xin2, ZHANG Wenxin1, 3, QIN Shuangyu1, 3

(1. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China;2. Geographic Information and Tourism College, Chuzhou University, Chuzhou 239000, China;3. National Administration of Surveying, Mapping and Geoinformation Key Laboratory of Land Environment and Disaster Monitoring, China University of Mining and Technology, Xuzhou 221116, China)

In order to establish the surface subsidence prediction model for dense solid backfilling mining, the strata movement and deformation characteristics were firstly analyzed using the drilling peep and similar material simulation model, which are different from that caused by caving mining method. Subsequently, the deflection formula of basic roof was obtained using the Winkler model and Vlazov model. The flexural subsidence of the basic roof can be regarded as the boundary condition for overlying strata subsidence. And then the surface subsidence prediction model was deduced based on the discrete media migration law. Finally, the established model was applied to theHuayuan coal mine. The results show that the subsidence prediction values are basically consistent with the measured values, confirming the accuracy of the prediction model.

dense solid backfilling mining; basic roof; elastic foundation beam; surface subsidence prediction

10.11817/j.issn.1672-7207.2017.09.030

TD325

A

1672−7207(2017)09−2491−07

2016−11−22；

2017−01−15

国家“十二五”科技支撑计划项目(2012BAB13B03)；江苏省高校优势学科建设工程资助项目(SZBF2011-6-B35)；江苏省普通高校研究生科研创新计划项目(KYLX15_1438) (Project(2012BAB13B03)supported by the National Science and Technology Pillar Program during the 12th “Five-year” Plan Period; Project(SZBF2011-6-B35) supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions; Project(KYLX15_1438) supported by the Research Innovation Program for College Graduates of Jiangsu Province)

郭广礼，博士，教授，从事开采沉陷及岩层控制方面的研究；E-mail: guoguangli65@163.com