Ti-6Al-2Zr-1Mo-1V板材热成形的韧性破裂准则
2017-10-12郭靖詹梅王贤贤赵彬王敏杨合
郭靖,詹梅,王贤贤,赵彬,王敏,杨合
Ti-6Al-2Zr-1Mo-1V板材热成形的韧性破裂准则
郭靖1,詹梅1,王贤贤1,赵彬1,王敏2,杨合1
(1. 西北工业大学材料学院,陕西西安,710072;2. 湖北汽车工业学院,湖北十堰,442025)
为精确预测Ti-6Al-2Zr-1Mo-1V板材热成形过程中的破裂现象,通过实验与有限元模拟相结合的方法建立基于C&L,R&T和Oyane的钛合金板材热成形韧性破裂准则。首先,进行不同温度及应变速率下的钛合金板材单轴等温拉伸实验,得到不同温度及应变速率下的破裂应变。随后,基于得到的破裂应变,利用有限元模拟及点追踪方法得到上述不同韧性破裂准则的损伤参数,通过引入Zener-Holloman参数,建立损伤参数随温度和应变速率变化的模型。最后,综合考虑变形历史、温度及应变速率对板材破裂的影响,建立基于C&L,R&T和Oyane准则的钛合金板材热成形韧性破裂准则,并将建立的韧性破裂准则应用到钛合金锥形件热旋成形破裂预测。研究结果表明:破裂应变随温度的升高和应变速率的降低而逐渐增大;不同韧性破裂准则的损伤参数随温度和应变速率的变化与破裂应变的相同;Oyane准则预测准确度最高。
Ti-6Al-2Zr-1Mo-1V板材;韧性破裂准则;热成形;有限元模拟
钛合金因为密度小、比强度高、抗腐蚀性能好、耐高温等优点而被广泛应用于航空、航天、兵器等领 域[1−3]。其中,钛合金板材因为满足产品轻量化、薄壁化的发展趋势,也得到了越来越广泛的关注和应用。在板材成形过程中,破裂是最主要的成形缺陷。对于钛合金板材来说,由于其属于密排六方结构,滑移系较少,成形性能较差;与此同时,塑性加工过程中的不均匀变形会导致钛合金板材在成形过程中更易出现破裂缺陷[4−5]。为使钛合金板材在热成形过程中不出现破裂,提升钛合金板材的成形极限,需要准确预测钛合金板材热成形过程中的破裂现象。目前,对板材成形过程中的破裂预测主要是利用韧性破裂准则来实 现[6−7]。韧性破裂准则根据连续损伤力学和细观损伤力学理论而建立,该理论认为材料发生韧性破裂与所处的应力、应变状态和自身的特性有关[8−10]。韧性破裂准则可以预测复杂应变路径下的板材成形破裂,同时,韧性破裂准则可以与有限元方法很好地结合,从而更加直观地预测板材成形过程中的破裂。目前,国内外学者针对韧性破裂准则进行了大量的研究。ZHAN 等[11]将C&L和Lemaitre准则嵌入到有限元模型中来预测铝合金板材旋压过程中的破裂,并与实验结果进行对比,验证了上述韧性破裂准则的适用性。YAN 等[12]则将R&T和Oyane等十几种韧性破裂准则嵌入到铝合金壁板压弯有限元模型中来验证不同准则的有效性,通过与实验对比,确定了最适用的韧性破裂准则。然而,人们对上述韧性破裂准则的研究都是针对板材室温成形过程进行的,而针对板材热成形过程,需要在韧性破裂准则中考虑温度和应变速率的影响。KIM 等[13]将温度和应变速率的影响通过Zener−Holloman常数来表示,建立了基于Freudenthal的热成形韧性破裂准则,该准则准确地预测了镁合金板材冲压过程中裂纹出现的位置。张士宏等[14]基于连续损伤力学,综合考虑变形历史(温度和应变速率)对损伤的累计演化和临界损伤值的影响,同样以Zener−Holloman常数为基础提出了一种新的韧性破裂预测方法。该方法准确地预测了镁合金和不锈钢热成形过程中的破裂。可以看到,上述研究方法将温度和应变速率耦合到韧性破裂准则中,准确地预测了板材热成形过程中的破裂缺陷。然而,目前板材热成形过程的韧性破裂准则研究主要针对镁合金、铝合金以及不锈钢,对于本文作者所研究的钛合金板材,研究报道较少。为了能准确预测钛合金板材热成形过程中的破裂,需要研究建立针对钛合金板材热成形的韧性破裂准则。为此,本文作者通过不同温度及应变速率下的Ti-6Al-2Zr-1Mo-1V板材单轴等温拉伸实验,利用有限元模拟技术,得到不同温度和应变速率下的不同韧性破裂准则的损伤参数。通过引入Zener−Holloman常数,建立适用于钛合金板材热成形过程的韧性破裂准则。
1 韧性破裂准则
板材成形过程中的破裂预测主要是采用非耦合的宏观韧性破裂准则[15−16]。非耦合宏观韧性破裂准则通常以应力、应变和微观变量的独立或组合形式来表达,该类韧性破裂准则认为在成形过程中损伤的产生不会影响材料的屈服,其主要形式如下[17]:
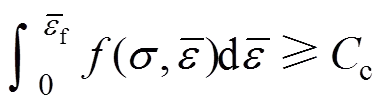
热成形过程中的破裂预测,需要在韧性破裂准则中考虑温度和应变速率的影响,同时也需要综合考虑变形历史对损伤积累和临界破裂值的影响,其形式为
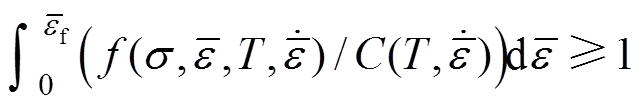
基于不同理论,韧性破裂准则有多种形式,不同形式的韧性破裂准则也有其适用范围。本文基于C&L,R&T和Oyane这3种韧性破裂准则建立针对钛合金板材热成形的韧性破裂准则。上述3种韧性破裂准则的形式如表1所示[17](其中,为等效应力;为最大主应力;为静水压力;为材料常数(本文中=3/2);1,2和3分别为C&L,R&T和Oyane准则的损伤常数)。

表1 韧性破裂准则简介
2 韧性破裂准则中损伤参数的获取
2.1 单轴等温拉伸实验
本文利用单轴等温拉伸试验来获得不同温度及应变速率下的破裂应变。试验方案如表2所示。每个编号实验进行2次以确保实验数据的准确和可靠。试样的设计依据金属材料高温拉伸试验方法GB/T 4338—2006来进行,实验设备为SANS CMT 5205电子拉伸试验机,通过实验机配备的炉子进行加热。拉伸实验通过位移来控制,拉伸过程一直持续到试样拉断,通过测量试样断后标距的伸长量来确定破裂时的应变。试样拉断后形貌如图1所示。不同温度及应变速率下的破裂应变如表2所示。由表2可知:破裂应变随温度的升高而增大,随应变速率的增加而减小。
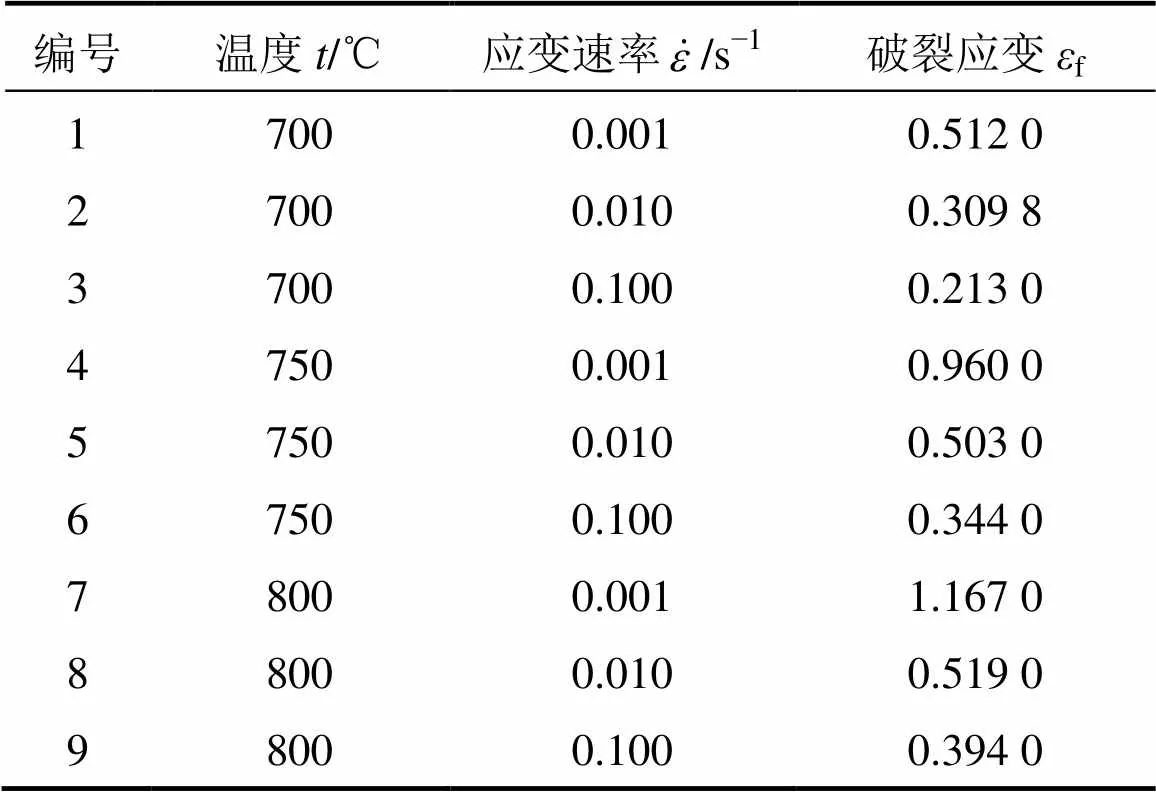
表2 拉伸试验方案及破裂应变

图1 拉伸试验后试样
2.2 损伤参数获取
损伤参数的获取是基于实验得到的破裂应变,通过有限元方法模拟实际拉伸过程,利用点追踪技术,得到应力应变历史积分。本文作者基于ABAQUS平台建立了尺寸、拉伸速度与实验相同的有限元模型,如图2所示。试样网格采用C3D8R单元,在试样标距段采用网格细化技术。网格密度越大,损伤参数越精确。考虑计算效率的影响,实验标距段网格大小为1 mm×1 mm。

图2 有限元拉伸模型
利用上述模型可以获得不同韧性破裂准则的损伤参数,具体步骤如下:
1) 观察模拟过程中第一主应变的最大值所处单元,当该值达到实验过程中的破裂应变时,即认为此处发生破裂。
2) 通过ABAQUS的子程序VUSDFLD,获取该单元对应损伤参数的SDV(状态变量),并提取可计算每一增量步的应力应变,从而依据公式求得损伤值(其中,为第+1增量步损伤参数,C为第增量步损伤参数)。
依据上述方法,可得表1中韧性破裂准则在不同温度和应变速率下的损伤参数值,如表3所示。
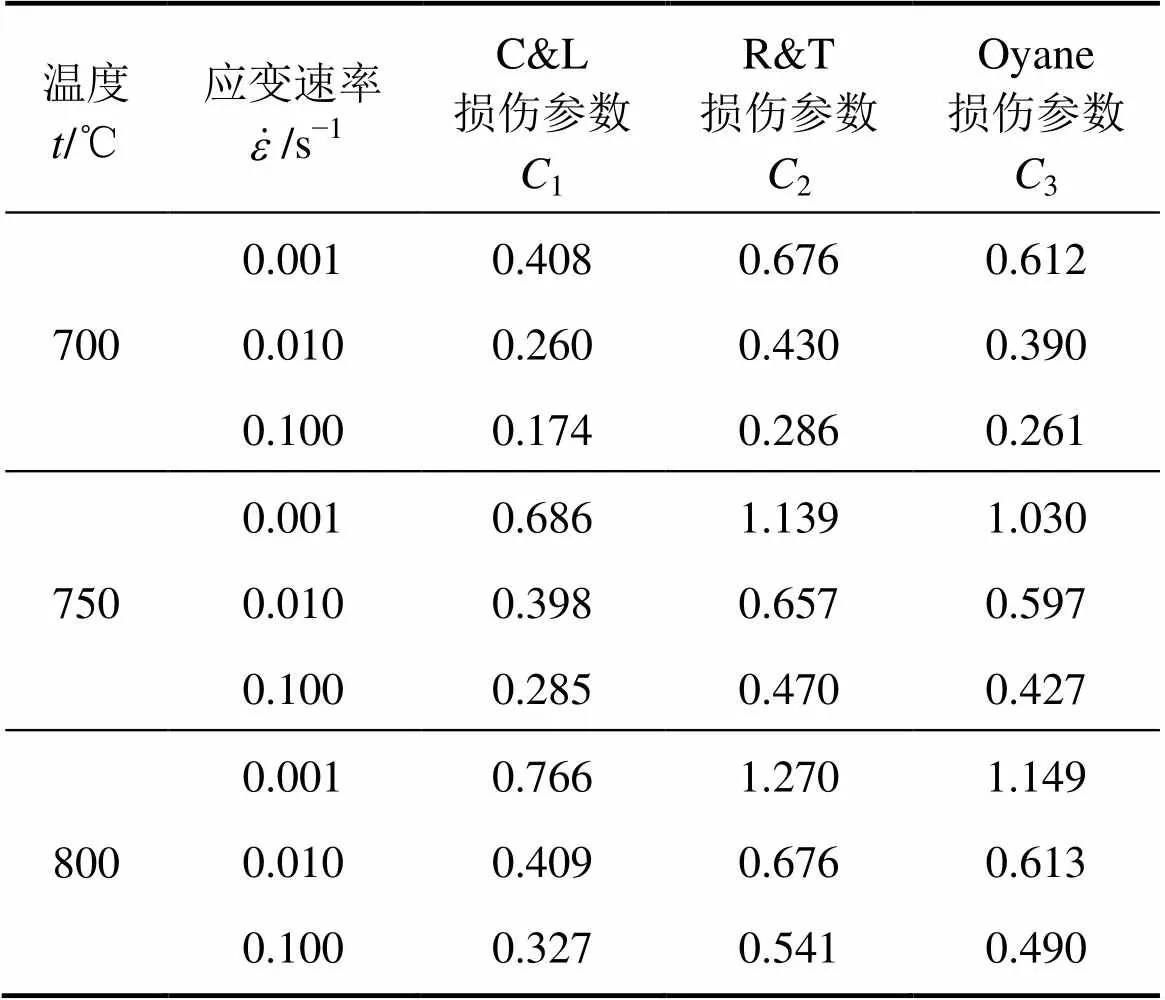
表3 损伤参数值
3 热成形韧性破裂准则建立
3.1 Zener−Holloman参数的引入
到目前为止,通常用Zener−Holloman参数来表征热成形过程中温度及应变速率的耦合作用。Zener−Holloman参数的表达式如下:

其中:为Zener−Holloman参数值;为应变速率;是摩尔气体常数;为激活能;为热力学温度。针对本文研究的Ti-6Al-2Zr-1Mo-1V板材热拉伸过程,=8.314 J/(mol·K),=570.76 kJ/mol[1]。
将损伤参数函数中温度和应变速率的影响用Zener−Holloman参数代替,则损伤参数变化函数如下:
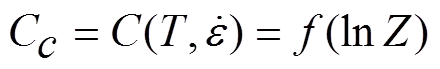
3.2 热成形韧性破裂准则的建立
基于表3中不同温度和应变速率下韧性破裂准则的损伤参数,可得到不同韧性破裂准则损伤参数与的关系,如图3所示。
利用Origin软件拟合图3所示的不同韧性破裂准则损伤参数与的对应关系,可分别得到C&L,R&T和Oyane准则损伤参数与的关系模型:
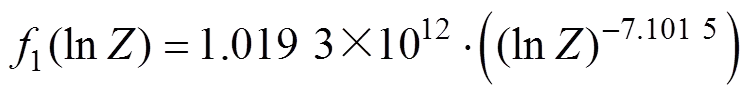
(6)
(7)

(a) C&L; (b) R&T; (c) Oyane
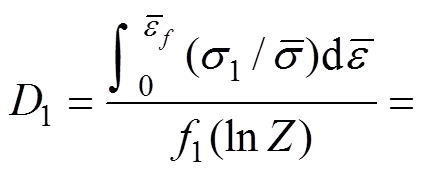
(8)
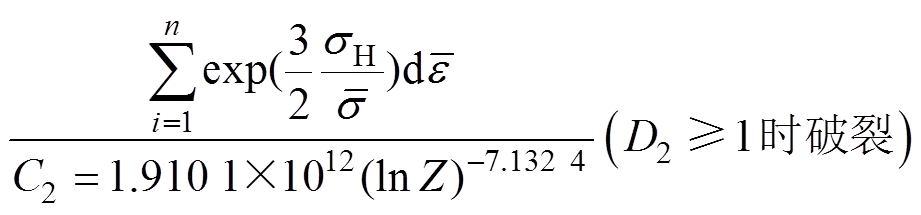
(10)
其中:式(8)为基于C&L准则的热成形韧性破裂准则;式(9)为基于R&T准则的热成形韧性破例准则;式(10)为基于Oyane准则的热成形韧性破裂准则;1,2和3分别为C&L,R&T和Oyane韧性破裂准则的相对损伤参数。
式(8)~(10)所示的热成形韧性破裂准则耦合了温度和应变速率的影响,同时也考虑了变形历史的影响作用。因此,对于不同的钛合金板材热成形工艺,可以针对性地选择式(8)~(10)中的韧性破裂准则,嵌入到有限元模型中,从而预测钛合金板材热成形过程中的破裂现象。
4 韧性破裂准则适用性及准确性
4.1 韧性破裂准则适用性
本文建立的C&L,R&T和Oyane韧性破裂准则,其适用范围不尽相同。LI等[17]针对上述韧性破裂准则的适用性进行了大量研究。
针对压缩变形行为,C&L和Oyane准则能准确预测破裂产生的位置,这是因为C&L准则考虑了最大拉应力对最终破裂的影响,Oyane准则考虑了应力三轴度对最终破裂的影响。而在R&T准则中,不能准确描述损伤的积累,因此,不能准确预测破裂产生的位置。
而对于拉伸变形行为,C&L,R&T和Oyane韧性破裂准则能准确预测破裂产生的位置,这是因为在拉伸变形中,颈缩的产生能使上述准则准确预测破裂产生的位置。
4.2 韧性破裂准则准确性
为验证本文所建立的C&L,R&T和Oyane韧性破裂准则的准确性,将上述韧性破裂准则应用于钛合金锥形件热旋压开裂的预测。
基于ABAQUS 平台建立锥形件热旋三维有限元模型,如图4所示。图中P为旋轮和芯模运动的参考点。模型参数如表4所示。材料模型通过Ti-6Al- 2Zr-1Mo-1V热拉伸试验获得。利用ABAQUS/Explicit 有限元平台的VUMAT子程序将C&L,R&T和Oyane韧性破裂准则耦合到有限元模型中,从而实现钛合金锥形件热旋压开裂的预测。
图5所示为C&L,R&T和Oyane准则预测锥形件热旋破裂的结果对比。其中,图5(a)所示为C&L准则预测结果,该准则预测成形时间=3.5 s,成形高度=2.9 mm时锥形件发生破裂。图5(b)所示为R&T准则预测结果,该准则预测成形时间=5 s,成形高度=8.4 mm时锥形件发生破裂。图5(c)所示为Oyane准则预测结果,该准则预测成形时间=5.25 s,成形高度=9.2 mm时锥形件发生破裂。图6所示为锥形件热旋实验结果,实验过程中的工艺参数与表4所示的模拟过程的工艺参数相同。在成形高度为10 mm时,锥形件发生了破裂。由图5~6可知:C&L,R&T和Oyane准则预测的破裂产生位置早于实验中裂纹产生的位置。其中,Oyane准则预测误差为8%,准确度最高;R&T准则预测误差为16%,准确度次之;C&L准则预测误差为70%,预测精度最低。
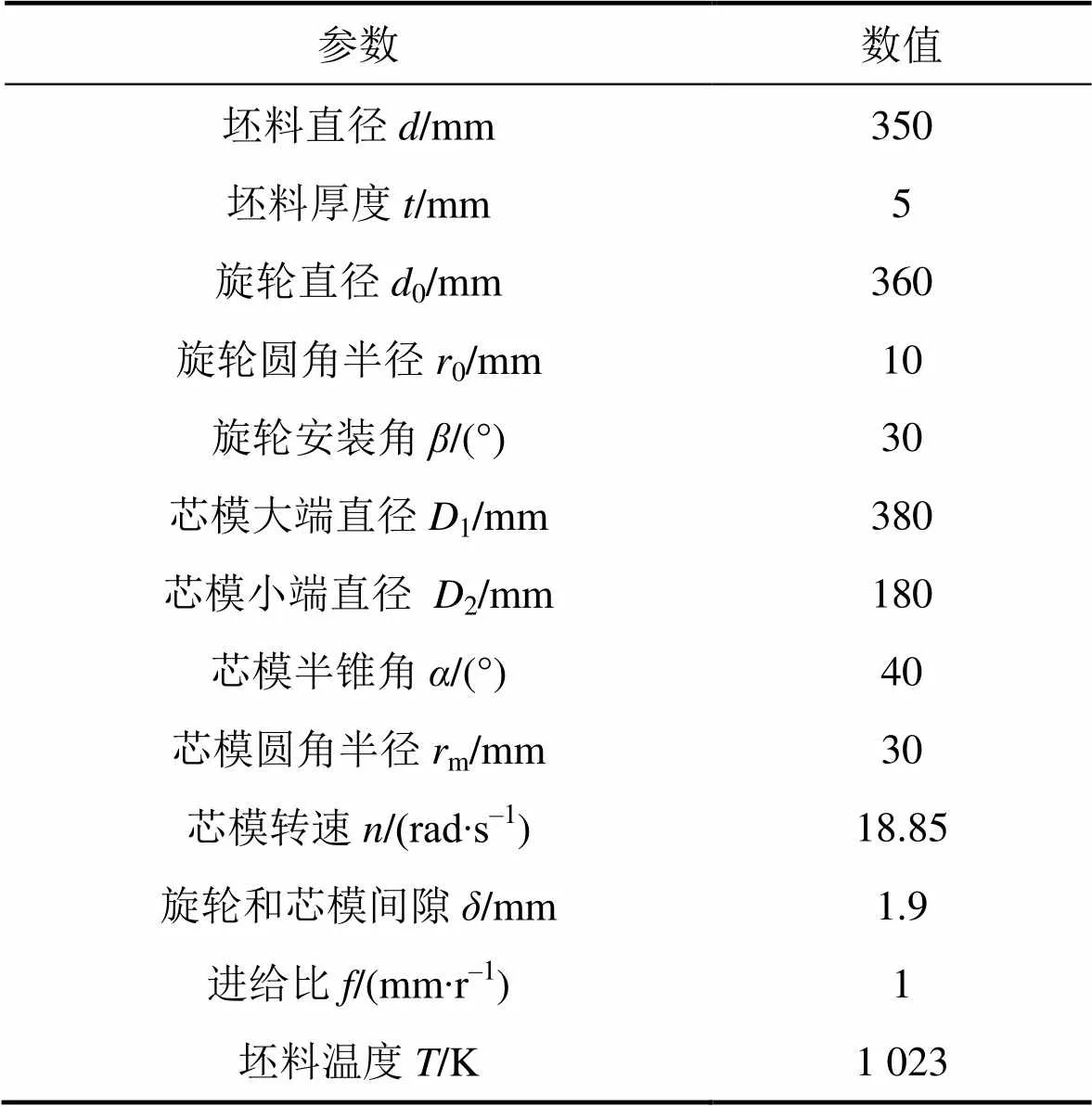
表4 锥形件热旋模拟参数
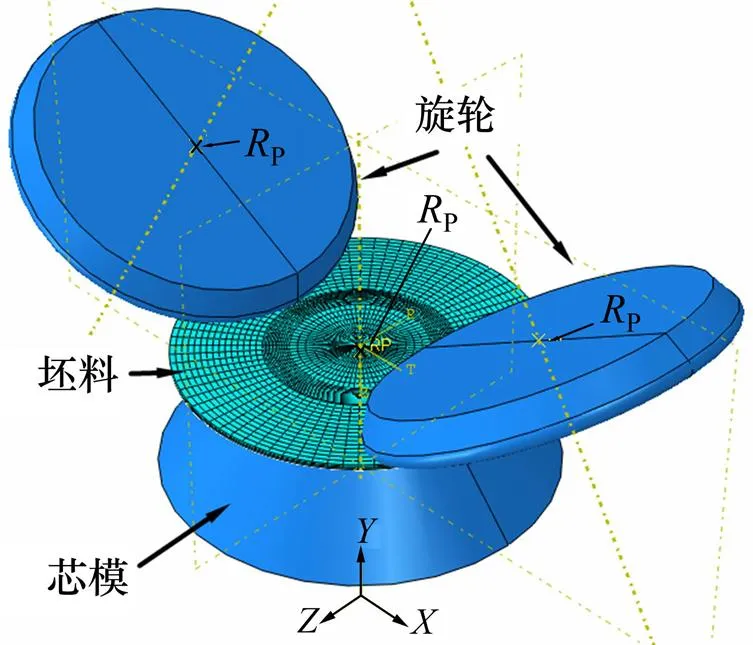
图4 锥形件热旋模型
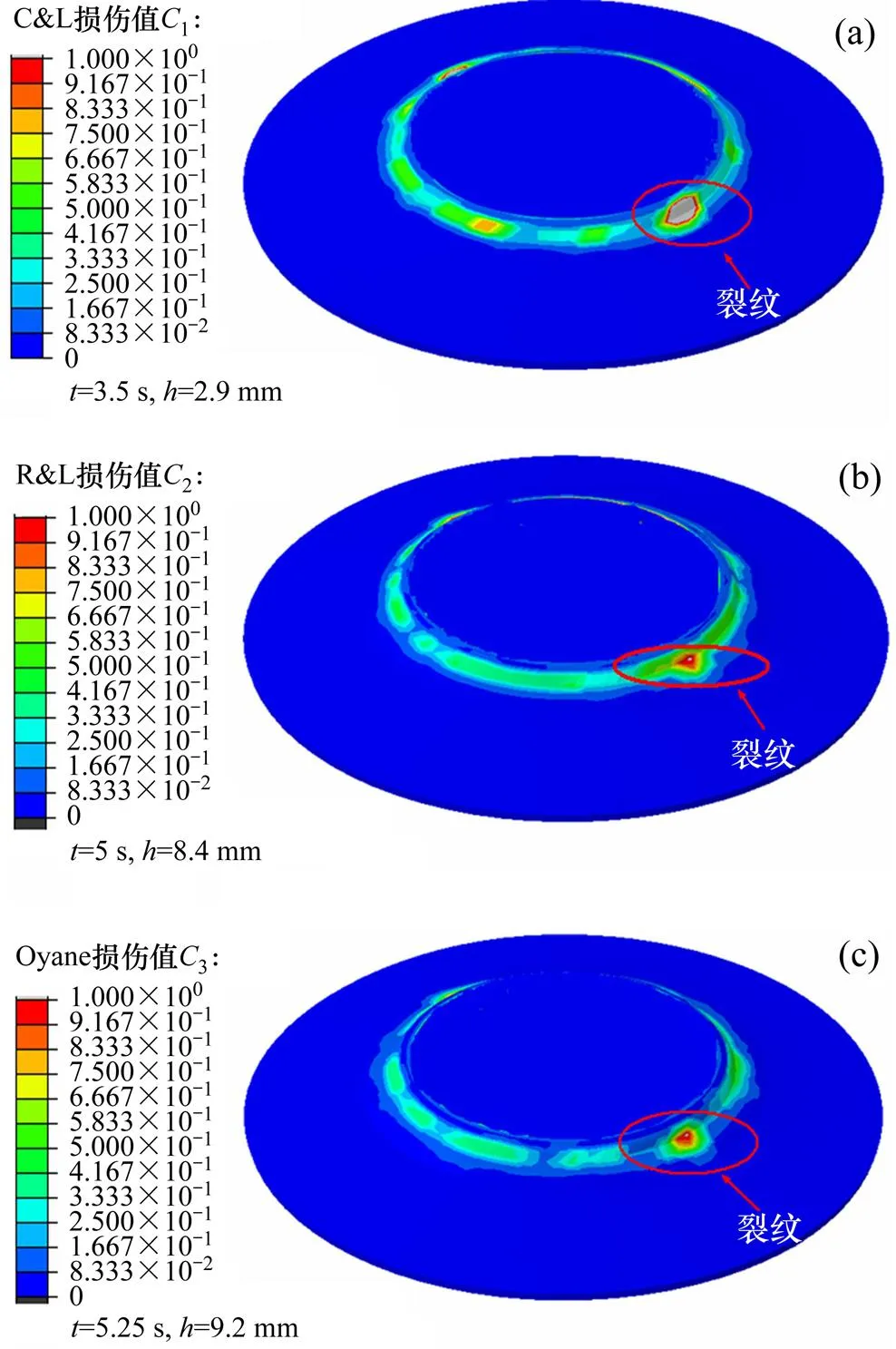
(a) C&L; (b) R&T; (c) Oyane

图6 锥形件热旋实验结果
5 结论
1) 建立Ti-6Al-2Zr-1Mo-1V板材热成形过程韧性破裂准则的实质是建立损伤参数与温度和应变速率的关系函数。选取C&L,R&T和Oyane这3种韧性破裂准则为基础建立钛合金板材热成形的韧性破裂准则。
2) 分别进行温度为700,750和800 ℃,应变速率为0.001,0.010和0.100 s−1下的等温单轴拉伸实验,获得不同条件下的破裂应变。破裂应变随温度的升高而增大,随应变速率的增大而减小。
3) 以ABAQUS为平台建立等温单轴拉伸实验模型。基于得到的破裂应变,利用ABAQUS子程序和点追踪方法得到不同温度和应变速率下C&L,R&T和Oyane准则的损伤参数。
4) 引入Zener−Holloman参数,最终建立损伤参数变化与温度和应变速率的模型。考虑变形历史对最终破裂的影响,建立基于C&L,R&T和Oyane准则的钛合金板材热成形韧性破裂准则。
5) 对于压缩变形行为,C&L和Oyane准则能准确预测破裂产生的位置,而R&T准则不能准确预测破裂产生的位置。而对于拉伸变形行为,C&L,R&T和Oyane韧性破裂准则能准确预测破裂产生的位置。
6) 针对锥形件热旋成形过程的破裂预测,Oyane准则预测准确度最高,R&T准则预测准确度次之,C&L准则预测准确度最低。
[1] HE Dong, ZHU Jingchuan, LAI Zhonghong, et al. An experimental study of deformation mechanism and microstructure evolution during hot deformation of Ti-6Al-2Zr-1Mo-1V alloy[J]. Materials & Design, 2013, 46: 38−48.
[2] FAN Xiaoguang, YANG He. Internal state variable based self consistent constitutive modeling for hot working of two-phase titanium alloys coupling microstructure evolution[J]. International Journal of Plasticity, 2011, 27(11): 1833−1852.
[3] KHAN A S, KAZMI R, FARROKH B. Multiaxial and non-proportional loading responses, anisotropy and modeling of Ti-6Al-4V titanium alloy over wide ranges of strain rates and temperatures[J]. International Journal of Plasticity, 2007, 23(6): 931−950.
[4] YANG Lei, WANG Baoyu, LIU Gang, et al Behavior and modeling of flow softening and ductile damage evolution in hot forming of TA15 alloy sheets[J]. Materials & Design, 2015, 85(15): 135−148.
[5] MA Hao, XU Wenchen, JIN Bocheng, et al. Damage evaluation in tube spinnability test with ductile fracture criteria[J]. International Journal of Mechanical Sciences, 2015, 100: 99−111.
[6] 郭玉琴, 王帅, 朱新峰, 等. B340/590DP钢温热成形破裂准则提出及成形极限预测[J]. 塑性工程学报, 2015, 22(3): 38−43. GUO Yuqin, WANG Shuai, ZHU Xinfeng, et al. Proposal of warm forming fracture criterion and forming limit prediction of B340/590 DP steel[J]. Journal of Plasticity Engineering, 2015, 22(3): 38−43
[7] LIN Yongcheng, LIU Yanxing, LIU Ge, et al. Prediction of ductile fracture behaviors for 42CrMo steel at elevated temperatures[J]. Journal of Materials Engineering and Performance, 2015, 24(1): 221−228.
[8] OYANE M, SATO T, OKIMOTO K, et al. Criteria for ductile fracture and their applications[J]. Journal of Mechanical Working Technology, 1980, 4(1): 65−81.
[9] 谢延敏, 于沪平, 陈军, 等. 板料成形中韧性断裂准则应用研究进展[J]. 工程设计学报, 2007, 14(1): 6−10. XIE Yanmin, YU Huping, CHEN Jun, et al. Recent advances of research on application of ductile fracture criteria in sheet metal forming process[J]. Chinese Journal of Engineering Design, 2007, 14(1): 6−10.
[10] 陈志英, 董湘怀. 基于GTN细观损伤模型的板料成形过程损伤分析[J]. 工程力学, 2009, 26(7): 238−244. CHEN Zhiying, DONG Xianghuai. Ductile damage analysis for fracture in sheet metal forming based on GTN mesoscopic damage model[J]. Engineering Mechanics, 2009, 26(7): 238−244.
[11] ZHAN Mei, GU Chuangguo, JIANG Zhiqiang, et al. Application of ductile fracture criteria in spin-forming and tube-bending processes[J]. Computational Materials Science, 2009, 47(2): 353−365.
[12] YAN Yu, WANG Haibo, WAN Min. Prediction of fracture in press bend forming of aluminum alloy high-stiffener integral panels[J]. Computational Materials Science, 2011, 50(7): 2232−2244.
[13] KIM W J, KIM H K, KIM W Y, et al. Temperature and strain rate effect incorporated failure criteria for sheet forming of magnesium alloys[J]. Materials Science and Engineering A, 2008, 488(1/2): 468−474.
[14] 张士宏, 宋鸿武, 徐勇, 等. 一种韧性断裂损伤力学建模方法及其应用[J]. 精密成形工程, 2012, 3(6): 27−32. ZHANG Shihong, SONG Hongwu, XU Yong, et al. A new modeling approach of ductile damage mechanics and its applications[J]. Journal of Netshape Forming Engineering, 2012, 3(6): 27−32.
[15] LOU Y, HUH H, LIM S, et al. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals[J]. International Journal of Solids and Structures, 2012, 49(25): 3605−3615.
[16] 古田. 高强钢热成形韧性断裂准则研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012: 2−5. GU Tian. Research on ductile fracture criterion of hot stamping[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2012: 2−5.
[17] LI Heng, FU Mingwang, LU Jian, et al. Ductile fracture: Experiments and computations[J]. International Journal of Plasticity, 2011, 27(2): 147−180.
(编辑 伍锦花)
Ductile fracture criterions for hot forming process of Ti-6Al-2Zr-1Mo-1V alloy sheets
GUO Jing1, ZHAN Mei1, WANG Xianxian1, ZHAO Bin1, WANG Min2, YANG He1
(1. School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China;2. Hubei University of Automotive Technology, Shiyan 442025, China)
To accurately predict the fracture during the hot forming process of Ti-6Al-2Zr-1Mo-1V alloy sheets, ductile fracture criterions(DFCs) for the hot forming process of titanium alloy sheets was proposed based on C&L, R&T and Oyane criterions by the combination method of experiments with finite element(FE) simulation. Firstly, uniaxial isothermal tension tests were conducted at different temperatures under various strain rates and the fracture strains were obtained. Then, with the fracture strains, the damage parameters of different DFCs were obtained by FE method and point trace method. By introducing the Zener−Holloman parameter, the damage parameter model considering the effects of temperature and strain rate was established. Finally, the DFCs for hot forming process of titanium alloy sheets based on C&L, R&T and Oyane criterions were established by considering the deformation history, temperature and strain rate. The established criteria was applied in the hot shear spinning process of titanium alloy. The results show that fracture strains increase with the increase of temperature and decrease of strain rate; the changes of damage parameters of different DFCs are the same as that of fracture strains; Oyane criterion is the most accurate in predicting the fracture occurrence.
Ti-6Al-2Zr-1Mo-1V alloy sheets; ductile fracture criterions; hot forming; finite element simulation
10.11817/j.issn.1672-7207.2017.09.006
TG146.3
A
1672−7207(2017)09−2294−07
2016−11−07;
2016−12−29
国家自然科学基金杰出青年基金资助项目(51625505);国家自然科学基金航天先进制造技术研究联合基金重点支持项目(U1537203);凝固技术国家重点实验室自主课题(97-QZ-2014;90-QP-2013);国家自然科学基金资助项目(51205116);湖北省自然科学基金资助项目(2014CFB628) (Project(51625505) supported by the National Natural Science Foundation for Distinguished Young Scholars of China; Project (U1537203) supported by the Key Program Project of the Joint Fund of Astronomy and National Natural Science Foundation of China; Projects(97-QZ-2014; 90-QP-2013) supported by the Research Fund of the State Key Laboratory of Solidification Processing; Project(51205116) supported by the National Natural Science Foundation of China; Project(2014CFB628) supported by the Natural Science Foundation of Hubei Province)
詹梅,博士,教授,博士生导师,从事塑性成形理论与工艺研究;E-mail: zhanmei@nwpu.edu.cn
