蛇形轧制对Al-Mg-Si合金板材剪切变形及织构影响的模拟
2017-10-12凌利月唐建国刘文辉张新明陈亮邓运来
凌利月,唐建国,刘文辉,张新明,陈亮,邓运来
蛇形轧制对Al-Mg-Si合金板材剪切变形及织构影响的模拟
凌利月1,唐建国1,刘文辉2,张新明1,陈亮1,邓运来1
(1. 中南大学材料科学与工程学院,湖南长沙,410083;2. 湖南科技大学机电工程学院,湖南湘潭,411201)
通过有限元模拟,探究蛇形轧制过程中异速比、错位量和压下量对AA6016铝合金板材曲率的影响,并比较对称轧制与蛇形轧制板材的厚向应变分布及轧制过程中的应变演变规律。研究结果表明:在一定异速比范围内(1.00~1.20),异速比越大,轧板越向慢辊弯曲;错位会引起轧板向上辊弯曲;压下量越大,轧板越弯向慢辊,但上述结论在有错位量、异速比小于1.05时并不成立。与对称轧制过程相比,蛇形轧制过程中板材接触剪切应力和应变呈对称分布,整个轧制过程表现出上表层正应变较大、下表层正应变较小,切应变整体向上平移;等效应变则变化不大。蛇形轧制在板材整个厚度方向引入了剪切应变,因此,能够获得均匀的近似<111>//ND剪切织构。
AA6016铝合金;蛇形轧制;剪切织构;有限元模拟
随着经济的快速发展,汽车的普及程度越来越高,汽车工业带来的能源短缺和排放污染愈加严重[1−3]。采用轻量化材料是实现降低能耗的重要途径,而以铝代钢是实现汽车轻量化的最有效方法之一[4]。6000系铝合金属于热处理可强化铝合金,具有较高的强度、较好的塑性和优良的耐腐蚀性,被看作是未来汽车车身板的理想材料[5]。但是,通过常规轧制方法生产的车身用铝合金板材,其塑性应变比、杯突值和弯曲半径均比IF钢(Interstitial-Free Steel,无间隙原子钢)的低。板材冲压性能差是制约铝合金板材性能的重要原因。板材的室温成形性能特别是可以通过调控晶体学织构来提高[6−7]。HU等[8]的研究表明:对于面心立方(FCC)金属,强的<111>//ND织构有利于提高,但铝合金内{111}<110>滑移系特性和轧制的简单变形特点决定了其轧制板材中难以形成<111>//ND织构。为了在宽幅铝板中形成较强的<111>//ND织构,国内外学者尝试通过非对称轧制方式在板材内部引入剪切变形。异步轧制[9−11]、单辊驱动轧制[12]、异通道轧 制[13−14]、锥辊轧制[15]、槽压制法[16−17]、连续剪切轧 制[18]等方法通过增加一些变形的非对称因素(如上下轧辊异速、上下辊径差、不同摩擦因数)和剪切通道的引入等,在板材内部引入强剪切变形来获得<111>// ND剪切织构,从而提高铝合金板材的成形性能。但以上非对称轧制板材板形不易控制,难以应用于商业生产。本文作者通过采用蛇形轧制[19]的方法,即将轧机的上下轧辊水平错位并调控它们的转速比,在常规轧制变形模式的基础上叠加剪切变形模式,以获得较大的剪切应变分量,从而获得<111>//ND织构。付垚等[20−22]对AA7150铝合金板材进行了蛇形轧制实验,当异速比固定不变时,随着错位量的增加,轧板弯曲程度先减小后增大。李学文[23]通过合理匹配异速比和错位量,在蛇形轧制过程中获得较平直的板材,同时相比常规对称轧制沿板材厚向可获得更均匀的剪切应变分布。然而,国内外关于蛇形轧制过程中板材的织构演变的报道较少。本文作者以汽车车身用AA6016铝合金为研究对象,通过有限元模拟,探究蛇形轧制异速比、错位量和压下量对板材弯曲的影响。比较蛇形轧制平直板材与对应压下量下的对称轧制板材的厚向应变分布,并探究轧制过程中板材表面接触应力、各层应变变化情况。以不同厚度位置的位移梯度作为输入参数,采用VPSC模型模拟轧制过程不同阶段、不同厚度层的织构分布,研究蛇形轧制对板材厚度方向织构分布的影响。
1 有限元模拟
利用ABAQUS有限元模拟软件构建二维有限元模型,使用ABAQUS/Standard求解器,采用静态分析方法进行轧制仿真模拟。
1.1 几何模型及网格划分
2个轧辊半径均为50 mm,设置属性为解析刚体。板材设置为弹塑性属性,长×宽为200 mm×25 mm。刚体错位量为0,4和6 mm;所研究压下量Δ为4,6和8 mm,分别建立不同错位量与压下量的有限元模型。为了避免轧板难以被轧辊咬入,非对称轧制轧板的前端设计成与轧缝相匹配的形状。网格划分时,为保证板材单元在变形前没有严重扭曲,提高后期剪切应变分析的准确性,对板材部件进行分割,具体分割位置如图1所示。采用具有沙漏控制功能的平面应变减缩积分单元(CPE4R)对轧板进行网格划分[23]。

图1 蛇形轧制轧件分割示意图
1.2 材料性能
轧板材料为AA6016铝合金,力学性能见表1。采用各向同性、均匀的弹塑性材料模型,以单向拉伸试验获得的应力应变为参考,绘得真实应力应变曲线,如图2所示。

表1 6016铝合金的力学性能
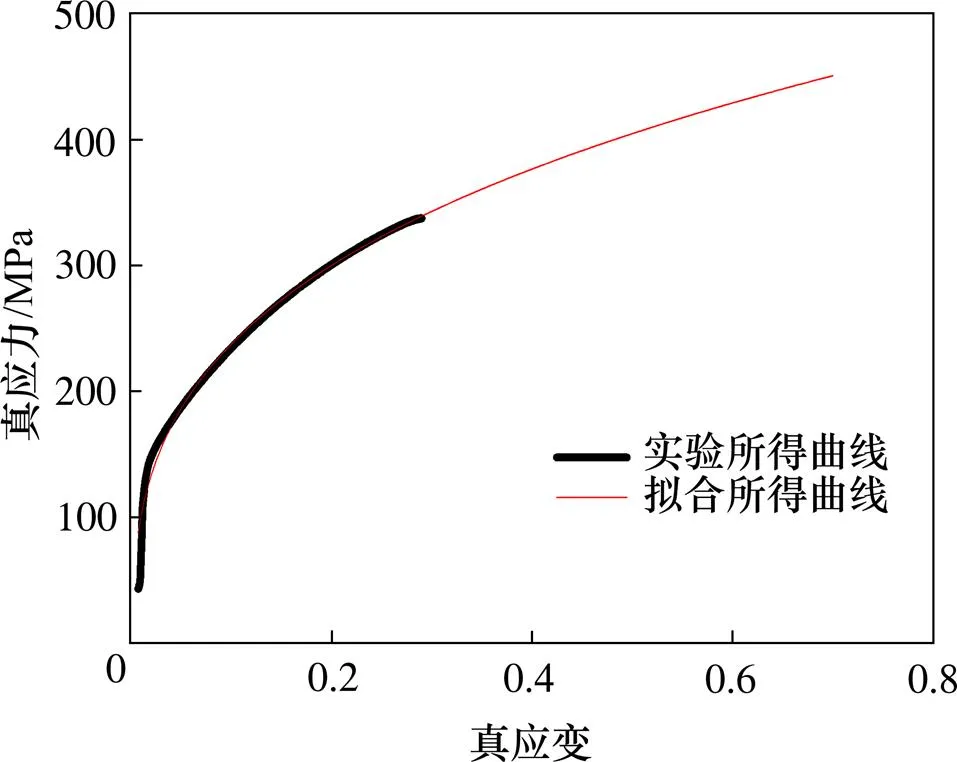
图2 真应力−真应变曲线
图2中的黑色粗线由实际得到的数据绘得。为了避免真应变大于0.3以后的真应力缺失,通过非线性曲线拟合,得到图中细线所示曲线,拟合函数为
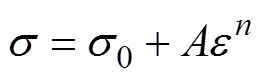
1.3 接触属性和边界条件
轧辊与轧板的摩擦在变形过程中起着重要作用。在轧制变形前,先建立一个轧辊与轧板稳定接触的分析步,使轧板可仅利用摩擦力被持续咬入。设置接触摩擦方式为库仑摩擦,摩擦因数为0.25。设置上、下辊的平移速度v和v均为0,固定下辊的旋转速度下=1.57 rad/s,旋转方向与上辊相反,上辊的转速上可调。模型所选取的上辊辊速及其对应异速比V=上/下如表2所示。

表2 模型辊速参数
注:上辊辊速为正向,下辊辊速为反向。
2 有限元模拟结果与讨论
2.1 蛇形轧制板材的弯曲行为
影响不对称轧制板材弯曲的因素较复杂,异速比、错位量以及压下量均对板材弯曲行为产生影响。当错位量=4 mm,压下量6 mm,异速比V不同时,蛇形轧制模拟的可视化结果见图3。由图3可以看出:上、下轧辊辊速相等时轧制板材向上弯曲;异速比为1.10以上时轧制板材向下弯曲,而异速比为1.05时板材平直。
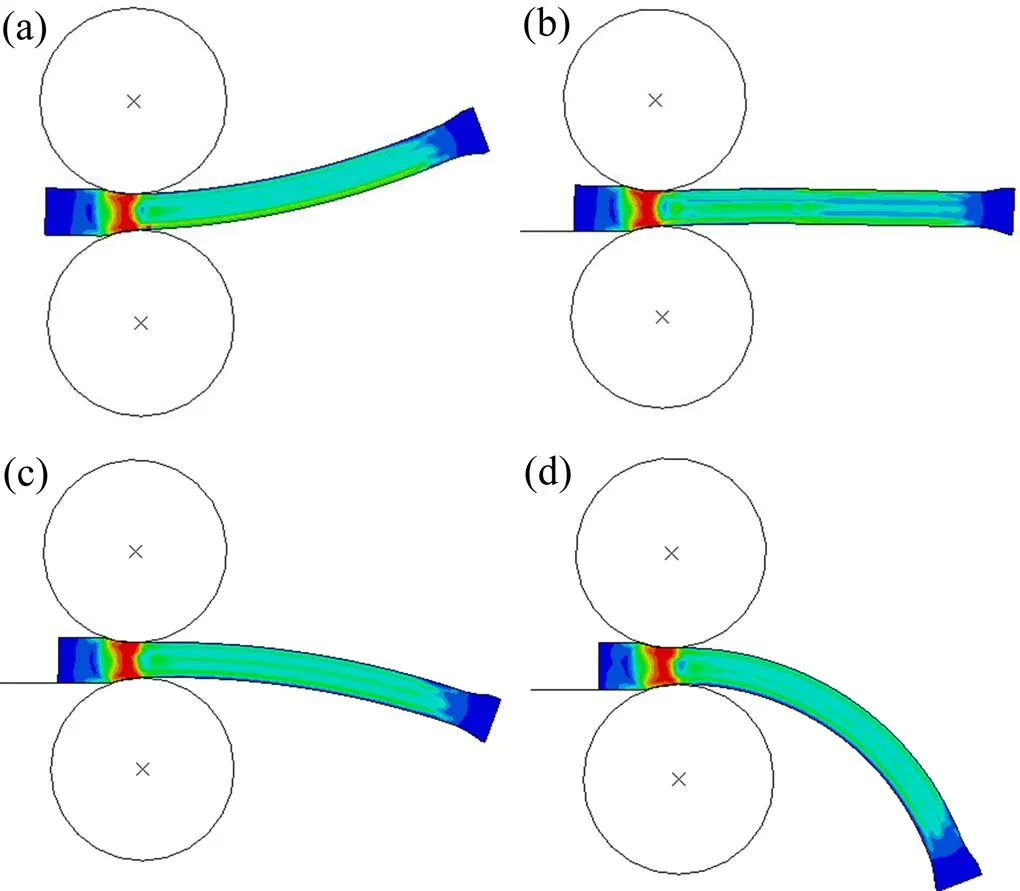
错位量Δ=4 mm,压下量Δh=6 mm
板材的平直程度可以用板材弯曲内侧的曲率来进行量化分析。规定板材向上弯曲时的曲率为正,向下弯曲的曲率为负。不同异速比、错位量、压下量对曲率的影响如图4所示。
由图4可以看出:异速比显著影响轧制板材的弯曲程度;无论何种错位量和压下量,当异速比为1.00时,板材曲率均最大;随着异速比增大,板材曲率均有减小,即向慢辊弯曲的趋势;当错位量为0时,显然异速比为1.00时板材最为平直,曲率为0;随着异速比增大,轧制板材渐渐向慢辊侧弯曲,即曲率为负。
由图4还可以发现:当异速比为1.00时,错位量越大,曲率也越大,即错位有引起板材向上弯曲的趋势;但在大压下量(Δ=8 mm)时,错位增加对板材曲率的改变并不明显;在其他异速比下,均有错位越大板材曲率越偏向正值的趋势,但在压下量Δ=8 mm时,小的错位量=0 mm曲线与=4 mm曲线重合,曲率变化一致。总体来说,错位会引起轧板向上辊弯曲,但在大压下量条件下,小错位量对曲率的影响并不明显。
压下量对板材曲率影响较复杂。对于无错位量(=0 mm)板材,压下量越大,曲率越小,轧板越弯向慢辊。而当有错位量、异速比小于1.05时,压下量Δ= 6 mm板材的曲率最大,Δ=4 mm板材曲率次之,而Δ=8 mm板材曲率最小;当异速比大于1.10时,压下量越大,曲率越小。
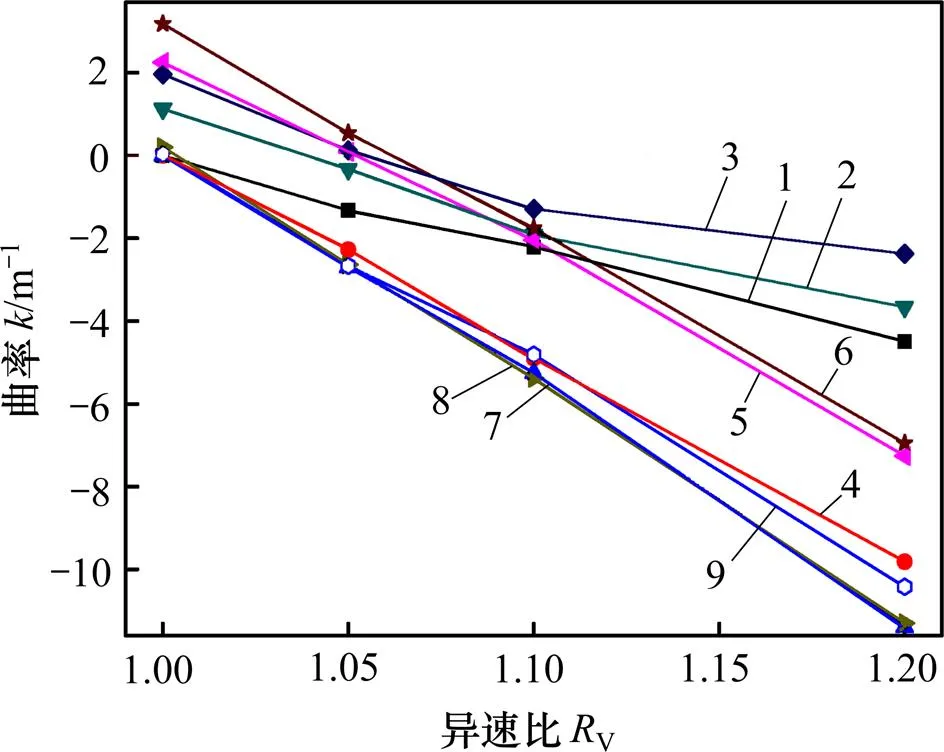
1—Δ=0 mm, Δh=4 mm; 2—Δ=4 mm, Δh=4 mm; 3—Δ=6 mm, Δh=4 mm; 4—Δ=0 mm, Δh=6 mm; 5—Δ=4 mm, Δh=6 mm; 6—Δ=6 mm, Δh=6 mm; 7—Δ=0 mm, Δh=8 mm; 8—Δ=4 mm, Δh=8 mm; 9—Δ=6 mm, Δh=8 mm。
2.2 蛇形轧制板材的应变分布
由图4可知:蛇形轧制中异速比V=1.05,错位量=4 mm,压下量Δ=6 mm的板材曲率最接近0,最为平直。为了便于描述,将该参数条件下轧制的板材称为蛇形轧制直板。选取该参数条件下的蛇形轧制和相应参数条件下的对称轧制(异速比V=1.00,错位量=0 mm和压下量Δ=6 mm)的有限元模型,对应变和演变进行有限元模拟分析,并以此模拟结果作为VPSC模拟条件研究蛇形轧制对织构演变的影响。
在2种轧制板材的稳定轧制区域分别选取任一列单元作为研究对象,各层位置用参数=2Δ/0(0为板材厚度,Δ为距中间层的距离)。厚向共分割成25个单元,从上而下依次编号1~25,用第1个和第25个单元分别表示板材最上层=+1.0和最下层=−1.0,第13个单元代表板材的中心层=0,第7个和第19个单元分别代表板材上次表层=+0.5和下次表层=−0.5。输出各单元轧制结束后的正应变,切应变和等效应变,分布情况如图5所示。
由图5可知:轧制后蛇形轧制板材应变表现出非对称分布;蛇形轧制板材上半部次表层以上部分 (>0.5)的正应变略大于常规对称轧制板材的对应部位的正应变,而在蛇形轧制板材上半部次表层以下部分(<0.5),正应变则小于对称轧制板材对应部位的正应变,这在下表层表现尤为明显(图5(a));蛇形轧制板材整体表现出上表层正应变较大,而下表层正应变较小的分布趋势。
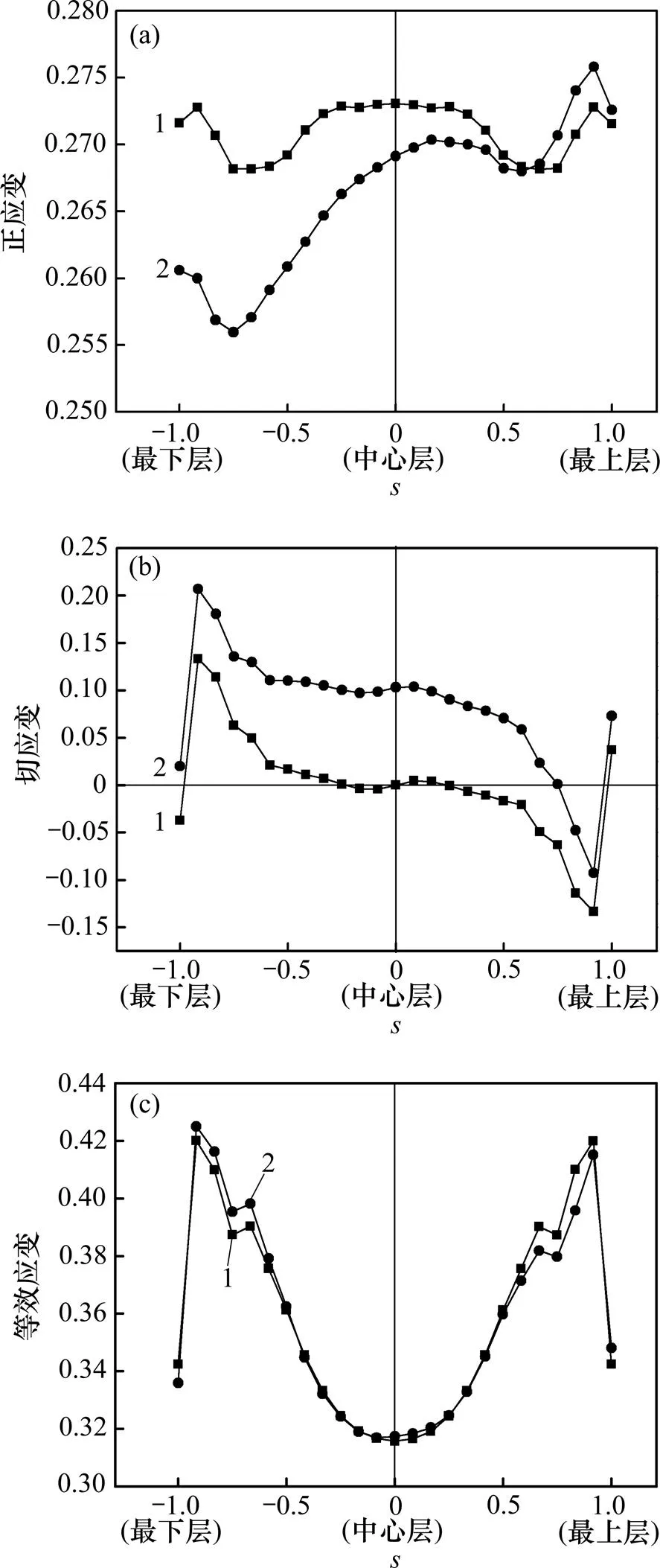
(a) 正应变;(b) 切应变;(c) 等效应变
与对称轧制板材相比,蛇形轧制板材中的剪切应变分布曲线整体上移,板材心部(=0)也获得了较大的剪切应变,整体的剪切应变都较大且分布厚度也远比对称轧制板材的厚度大。上、下表面单元的剪切应变受摩擦影响较大,其分布规律不同于板材内部;而板材内部的切应变受变形几何影响较大,蛇形轧制表现出>0.5的上表层切应变为负,而<0.5的上1/4层至下表层切应变整体为正,且较大(图5(b))。
蛇形轧制板材上表层等效应变比对称轧制板材的略小,下表层等效应变比对称轧制板材的略大。整体来看,2种方法轧制板材的等效应变相差不大(图5(c))。
2.3 蛇形轧制板材的轧制过程接触剪切应力和应变变化情况
在蛇形轧制过程中,轧板上、下部分的变形关于中心线不对称,因此,上、下接触面的接触剪切应力分布也不相同。追踪所研究单元的上、下表面最左侧节点的接触剪切应力变化情况,以最初接触剪切应力不为0 MPa的位置作为基准,精确绘制轧制区不同相对位置的接触剪切应力分布情况。图6所示为蛇形轧制和对称轧制轧板变形区的接触剪切应力分布情况。由图6可以看出:蛇形轧制上下表面中性点并不重合,上表面(快速辊侧)中性点NP1偏向出口侧,下表面(慢速辊侧)的中性点NP2偏向入口侧。与对称轧制相比,蛇形轧制除了前滑区和后滑区,在上、下表面中性点间形成了搓轧区。
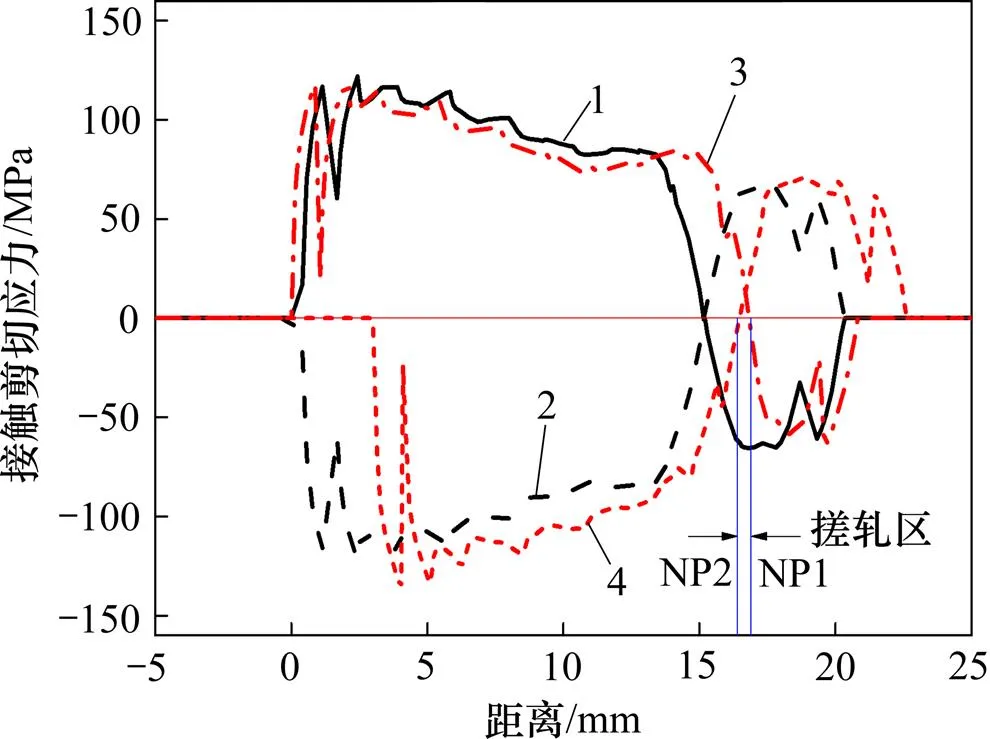
1—对称轧制CR,s=1.0;2—对称轧制CR,s=−1.0;3—蛇形轧制SR,s=1.0;4—蛇形轧制SR,s=−1.0。
处于稳定后滑区时,蛇形轧制上表面接触剪切应力数整体比对称轧制的小,下表面接触剪切应力比对称轧制的大;而处于前滑区时,2种轧制过程中板材上、下表面接触剪切应力相差不大。
蛇形轧制中错位和异速的非对称因素也引起整个轧制区应变的非对称分布。由于表面单元受摩擦影响较大,故不选取表面单元对轧制过程应变进行对比。从上而下选取第2,7,13,19和24单元为研究对象,分别对应轧板上表层=0.9、上次表层=0.5、轧板中心=0、下次表层=−0.5、下表层=−0.9。图7所示为蛇形轧制和对称轧制轧板变形区不同厚度处正应变变化图。由图7可以看出:对称轧制、蛇形轧制呈现出类似的正应变变化趋势;整体上,先是次表层正应变较大,轧制稳定后表层正应变比次表层的高;整个蛇形轧制区上表层、上次表层正应变均比相应的下表层、下次表层的正应变明显要高,这种非对称分布一直保留到最终轧制完成(见图5(a))。
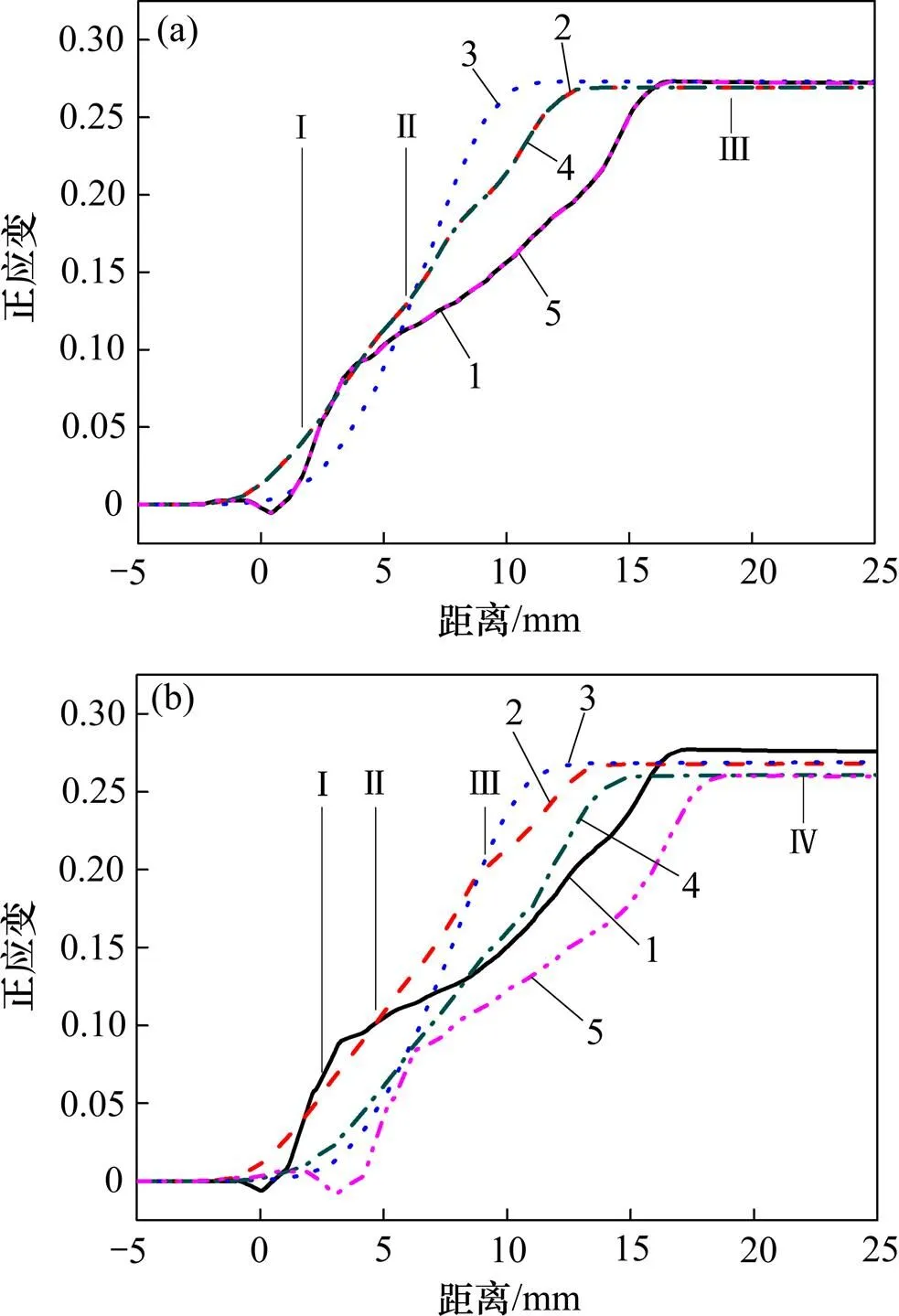
(a) 对称轧制;(b) 蛇形轧制
图8所示为蛇形轧制和对称轧制变形区轧板不同厚度处切应变变化图。由图8可以看出:与对称轧制相比,蛇形轧制心部剪切应变随着轧制进行逐渐增大,最后趋于稳定;蛇形轧制上表层切应变先达到绝对值的最大值,上次表层略先于下表层达到绝对值的最大值;随着轧制的进行,上次表层发生切应变方向翻转,最终相对于对称轧制厚度方向所有切应变向上平移(见图5(b))。
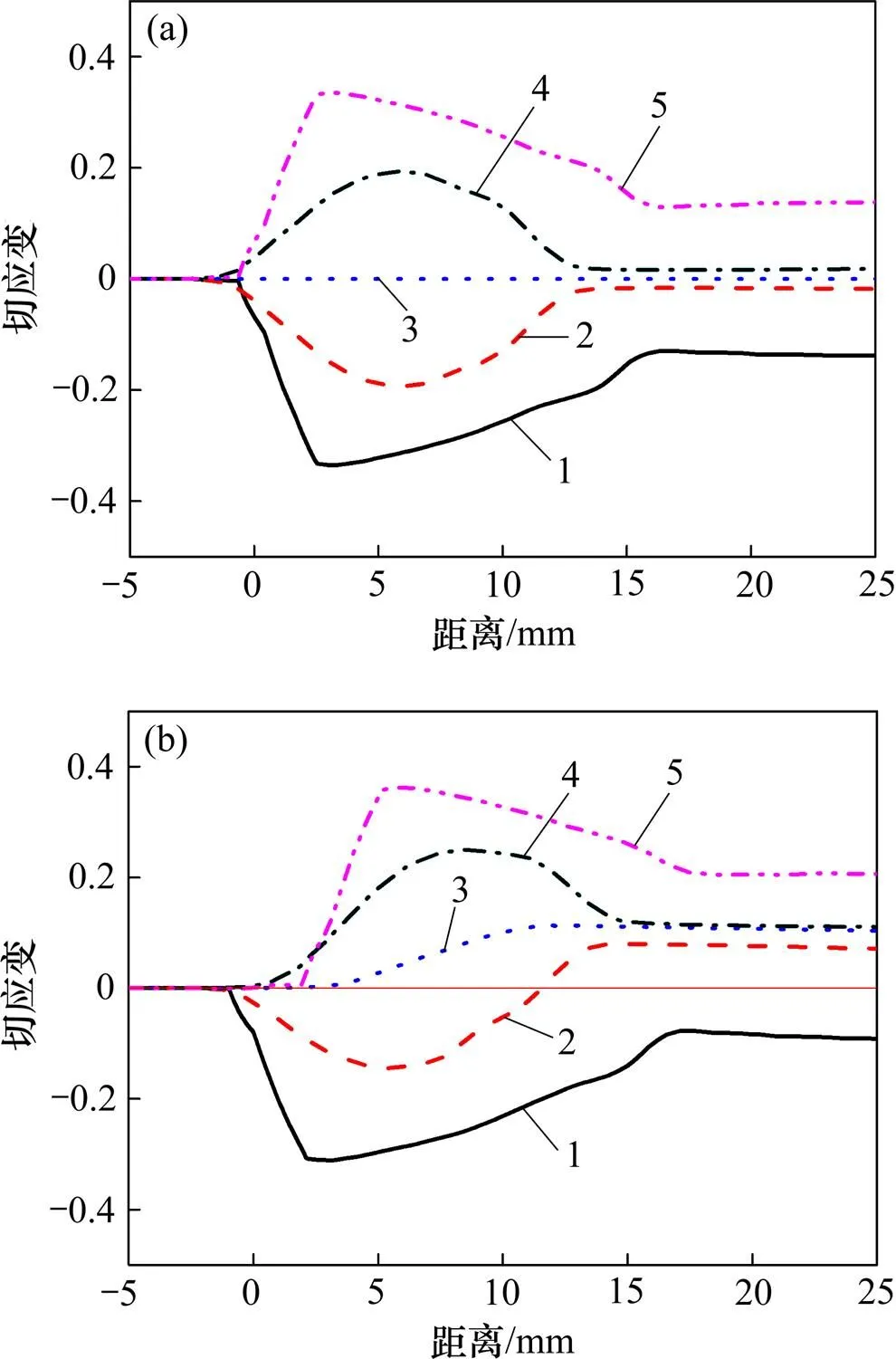
(a) 对称轧制;(b) 蛇形轧制
3 VPSC织构模拟结果与讨论
为探究蛇形轧制过程中板材厚向各层织构演变情况,采用粘塑性自洽(VPSC)模型对以上蛇形轧制直板和对称轧制板材织构演变进行模拟。由图6~8可知轧板进入前滑区后,接触剪切应力、应变变化均较小,因此,主要选取后滑区过程进行织构演变研究。其中,对称轧制以第13,19和24单元(从上而下)分别代表轧板中心、次表层和表层,输出3个单元在图7(a)Ⅰ~Ⅲ这3个阶段中的位移梯度,并将各阶段的位移梯度变化量及前一阶段模拟织构的结果作为VPSC的输入参数来模拟织构演变[24]。织构模拟前,选取500组随机取向来近似板材轧制前无织构的初始状态。再将VPSC模拟结果导入Mtex-3.1[25],画出{111}极图。蛇形轧制从上而下选取第2,7,13,19和24单元为研究对象,分别代表轧板上表层=0.9、上次表层=0.5、轧板中心=0.0、下次表层=−0.5、下表层=−0.9。输出5个单元在图7(b)Ⅰ~Ⅳ这4个阶段中的位移梯度进行VPSC织构模拟。对称轧制和蛇形轧制厚向各层织构演变{111}极图如图9和图10(密度间隔为0.2)所示。
由图9~10可以看出轧制过程中轧板的织构组分发生了显著的变化。由图9可知:在轧板刚咬入到轧制区时(第Ⅰ阶段),对称轧制表层和次表层首先发生变形,形成剪切织构,而中心并未形成明显的织构。当轧制进行到阶段Ⅱ,轧板中心受到平面应变变形,{111}极图表现为正交对称的特点,板材各层织构最大极密度值均增大,尤其是次表层织构显著增强。第Ⅲ阶段轧制结束,表层、次表层剪切织构减弱,心部呈现典型的取向线织构,{111}极图呈正交对称性。
由图10可知:蛇形轧制刚进入轧制区时(第Ⅰ阶段),轧制单元仅与上辊接触,轧板上表层首先变形,受剪切变形影响形成剪切织构;当轧制进行到位置Ⅱ时,单元开始与上、下两辊接触,上次表层、下次表层、下表层最大极密度显著增大,表层、次表层均形成一定的剪切织构,但中心部位的正应变和切应变均近似为0(图7(b)和图8(b)),没有形成明显的织构(此阶段与对称轧制的Ⅰ阶段相似);当轧制进行到位置Ⅲ时,上次表层极密度略有减小,下次表层极密度最大值增加并达到各层最大值,此时轧板心部已开始变形,织构绕TD方向转向RD负方向,{111}极图不再具有正交对称性,形成剪切织构特征。轧制完成后(阶段Ⅳ),上表层织构最强,心部保留剪切织构特征,最终沿厚向各层均能得到剪切织构。
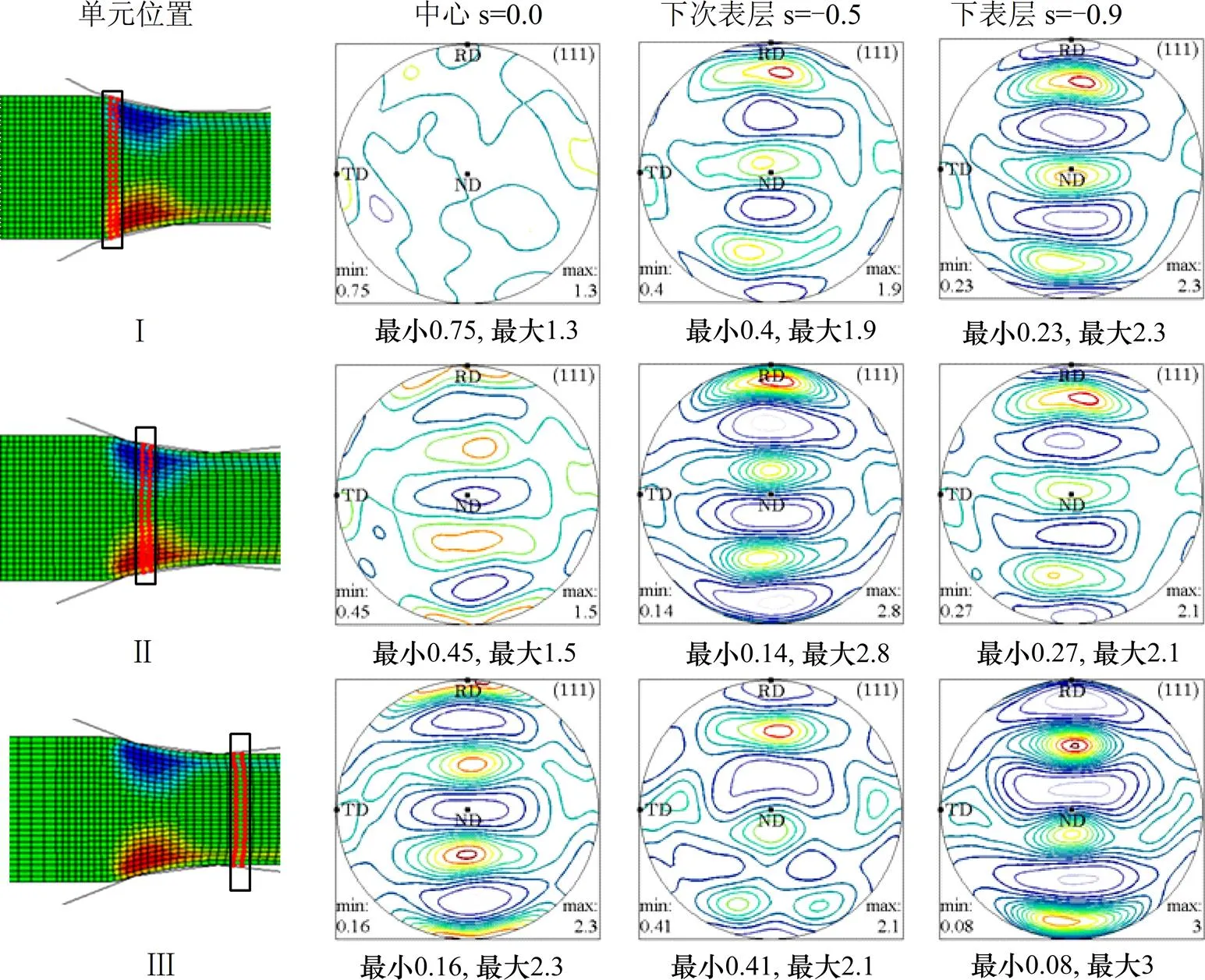
图9 对称轧制轧板厚向各层织构演变

图10 蛇形轧制轧板厚向各层织构演变
4 结论
1) 在1.00~1.20异速比范围内,随着异速比的增大,板材向慢辊侧弯曲的趋势增大;上辊相对于下辊偏向入口侧的错位量导致轧制板材有向上弯曲的趋势。在0~6 mm的错位量范围内,随着错位量的增大,向上弯曲的趋势增大,但在大压下量时小错位量对曲率影响并不明显。异速和错位的共同作用使得蛇形轧制在异速比V=1.05,错位量=4 mm和压下量Δ= 6 mm的轧制条件下能够轧出具有较大剪切应变的平直板材。
2) 蛇形轧制直板整体表现出上表层正应变较大,而下表层较小;切应变相对于对称轧制整体向上平移,尤其是心部也可获得剪切应变。2种轧制方法所得等效应变相差不大。
3) 蛇形轧制接触剪切应力和应变沿厚度方向呈现非对称分布。蛇形轧制后滑区上表面接触剪切应力整体比对称轧制的小,下表面接触剪切应力比对称轧制的大,而处于前滑区时2种轧制上、下表面接触剪切应力相差不大。蛇形轧制整个轧制区的上表层、上次表层正应变均比下表层、下次表层的明显要高,这种非对称分布一直保留到最终轧制完成。蛇形轧制心部也可产生剪切应变,并随着轧制进行逐渐增大,最后趋于稳定。
4) 蛇形轧制板材织构演变也呈非对称分布。其中,靠近快辊表层最先受到剪切变形的影响,最终织构强度最高;轧板心部也形成剪切织构特征,最终沿厚向各层均能得到<111>//ND剪切织构。
[1] MILLER W S, ZHUANG L, BOTTEMA J, et al. Recent development in aluminium alloys for the automotive industry[J]. Materials Science and Engineering: A, 2000, 280(1): 37−49.
[2] HIRSCH J, AL-SAMMAN T. Superior light metals by texture engineering: optimized aluminum and magnesium alloys for automotive applications[J]. Acta Materialia, 2013, 61(3): 818−843.
[3] HIRSCH J. Recent development in aluminium for automotive applications[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 1995−2002.
[4] 刘星兴, 唐建国, 张新明, 等. 双级淬火对车身板用6016铝合金烤漆硬化效应的影响[J]. 中国有色金属学报, 2014, 24(5): 1186−1193.LIU Xingxing, TANG Jianguo, ZHANG Xinming, et al. Influence of interrupted quenching on paint-bake response of AA6016 A1 alloy sheet[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(5): 1186−1193.
[5] 张新明, 刘星兴, 唐建国, 等. 复合添加Mn,Cr和Sr对车身用6016合金组织与力学性能的影响[J]. 中南大学学报(自然科学版), 2014, 45(12): 4152−4160.ZHANG Xinming, LIU Xingxing, TANG Jianguo, et al. Effect of Mn, Cr and Sr joint added on microstructure and mechanical properties of 6016 alloy used for automotive body sheets[J]. Journal of Central South University: Science and Technology, 2014, 45(12): 4152−4160.
[6] CHEN L, TANG J G, LIU S D. Through-thickness strain and texture gradients of Al-Mg-Si-Cu alloy sheets produced by snake rolling[J]. Applied Mechanics and Materials, 2014, 628: 79−83.
[7] ENGLER O, KIM H C, HUH M Y. Formation of {111} fibre texture in recrystallised aluminium sheet[J]. Materials Science and Technology, 2001, 17(1): 75−86.
[8] HU J, IKEDA K, MURAKAMI T. Effect of texture components on plastic anisotropy and formability of aluminium alloy sheets[J]. Journal of Materials Processing Technology, 1998, 73(1/2/3): 49−56.
[9] JIN H, LLOYD D J. Evolution of texture in AA6111 aluminum alloy after asymmetric rolling with various velocity ratios between top and bottom rolls[J]. Materials Science and Engineering A, 2007, 465(S1/2): 267−273.
[10] KIM H K, KIM H W, CHO JH, et al. High-formability Al alloy sheet produced by asymmetric rolling of strip-cast sheet[J]. Materials Science and Engineering A, 2013, 574: 31−36.
[11] SIDOR J, MIROUX A, PETROV R, et al. Microstructural and crystallographic aspects of conventional and asymmetric rolling processes[J]. Acta Materialia, 2008, 56(11): 2495−2507.
[12] SAKAI T, HAMADA S, SAITO Y. Improvement of the r-value in 5052 aluminum alloy sheets having through-thickness shear texture by 2-pass single-roll drive unidirectional shear rolling[J]. Scripta Materialia, 2001, 44(11): 2569−2573.
[13] HAN J H, SUH J Y, JEE K K, et al. Evaluation of formability and planar anisotropy based on textures in aluminum alloys processed by a shear deforming process[J]. Materials Science and Engineering A, 2008, 477(1/2): 107−120.
[14] LEE J C, SEOK H K, HAN J H, et al. Controlling the textures of the metal strips via the continuous confined strip shearing(C2S2) process[J]. Materials Research Bulletin, 2001, 36(5/6): 997−1004.
[15] CHINO Y, HUANG X, SUZUKI K, et al. Variation in texture and lankford value of 1070 aluminum sheet rolled by cone-shaped roll[J]. Journal of Materials Science and Technology, 2013, 29(2): 175−179.
[16] NIRANJAN G G, CHAKKINGAL U. Deep drawability of commercial purity aluminum sheets processed by groove pressing[J]. Journal of Materials Processing Technology, 2010, 210(11): 1511−1516.
[17] PARK J J, PARK N J. Influence of orthogonal shear on texture and R value in aluminum sheet[J]. Journal of Materials Processing Technology, 2005, 169(2): 299−307.
[18] SAITO Y, UTSUNOMIYA H, SUZUKI H, et al. Improvement in the r-value of aluminum strip by a continuous shear deformation process[J]. Scripta Materialia, 2000, 42(12): 1139−1144.
[19] Van Der WINDEN M R. Method for processing a continuously cast metal slab or strip. EP1420896B1[P]. 2007−04−11.
[20] 付垚, 谢水生, 熊柏青, 等. 主应力法计算蛇形轧制的轧制力[J]. 塑性工程学报, 2010, 17(6): 103−109.FU Yao, XIE Shuisheng, XIONG Baiqing, et al. Calculation of rolling force in snake rolling by slab method[J]. Journal of Plasticity Engineering, 2010, 17(6): 103−109.
[21] 付垚, 谢水生, 黄国杰, 等. 高强高韧铝合金厚板的蛇形轧制技术[J]. 铝加工, 2012(2): 18−22.FU Yao, XIE Shuisheng, HUANG Guojie, et al. Snake rolling of extra-thick plate with high strength and toughness[J]. Aluminium Fabrication, 2012(2): 18−22.
[22] 付垚. 高强高韧铝合金厚板的蛇形轧制研究[D]. 北京: 北京有色金属研究总院, 2011: 24−85.FU Yao. Research on snake rolling of thick plate of high strength and toughness aluminum alloy[D]. Beijing: General Research Institute for Nonferrous Metal, 2011: 24−85.
[23] 李学文. AA7050铝合金异步及水平错位非对称轧制变形的有限元模拟[D]. 长沙: 中南大学材料科学与工程学院, 2013: 18−64.LI Xuewen. Finite element modeling of deformation in AA7050 during asymmetric rolling with speed mismatch and horizontal displacement[D]. Changsha: Central South University. School of Materials Science and Engineering, 2013: 18−64.
[24] LEBENSOHN R A, TOMÉ C N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys[J]. Acta Metallurgica et Materialia, 1993, 41(9): 2611−2624.
[25] HIELSCHER R, SCHAEBEN H. A novel pole figure inversion method: specification of the MTEX algorithm[J]. Journal of Applied Crystallography, 2008, 41(6): 1024−1037.
(编辑 伍锦花)
Numerical simulation evolution of shear strain and crystallographic textures during snake rolling of Al-Mg-Si alloy plate
LING Liyue1, TANG Jianguo1, LIU Wenhui2, ZHANG Xinming1, CHEN Liang1, DENG Yunlai1
(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;2. College of Electromechanical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
The influences of velocity difference, horizontal offset between two rollers and pass reduction on bending behavior of AA6016 aluminum alloy plate in snake rolling (SR) were investigated by finite element simulations. The through-thickness distribution and evolution of strain in SR were compared with that in conventional symmetry rolling (CR). The results show that within certain velocity ratio (1.00~1.20) the plates tend to bend to the slower roller when velocity ratio increases. With the increase of the offset distance, the plates tend to bend to the faster roller. Greater pass reduction can lead to bending to the slower roller, except when there is horizontal offset and the velocity ratio is less than 1.05. In comparison with CR, the distribution of contact shear stress and strain of SR is asymmetric, normal strain of upper surface layer is larger than that of the lower surface layer, and the distribution of shear strain shifts upward. But there is no obvious difference in equivalent strain. With the introduction of shear deformation in the snake-rolled sheet in, it is easier to form through-thickness <111>//ND (Normal direction) texture.
AA6016 aluminum alloy; snake rolling; shear texture; finite element simulation
10.11817/j.issn.1672-7207.2017.09.004
TG335.5
A
1672−7207(2017)09−2279−09
2016−12−17;
2017−02−16
国家自然科学基金资助项目(51474240,51475162) (Projects(51474240,51475162) supported by the National Natural Science Foundation of China)
唐建国,副教授,博士研究生导师,从事金属材料织构与微结构表征、设计及调控技术研究;E-mail: jgtang@csu.edu.cn
