基于BEM的风力机叶片形变及气动性能

何佳，肖杨，邓友汉，巫世晶



基于BEM的风力机叶片形变及气动性能

何佳1, 2，肖杨1，邓友汉3，巫世晶1

(1. 武汉大学动力与机械学院，湖北武汉，430072；2. 三峡新能源利川风电有限公司，湖北利川，445400；3. 长江电力股份有限公司三峡电厂，湖北宜昌，443000)

为研究叶片形变对风力机气动性能的影响，提出基于叶素动量理论的叶片形变及气动性能研究方法，建立叶片在弹性形变下的形变量计算和气动载荷修正模型，通过改进的叶素动量理论与计算结构力学耦合迭代进行求解，并计算1 500 kW风力机叶片不同风速下的弹性形变量及对气动性能的影响。研究结果表明：所提算法可快速计算叶片弹性形变，用于叶片气动外形与结构设计的修正；可计算叶片等效攻角差值及其补偿角，用于优化风力发电机组变桨控制算法。

风力机叶片；气动弹性；耦合分析；扭转角；挠曲角；气动性能

大型风力机叶片尺寸大，叶片具一定柔性，在外部载荷作用下产生的弹性形变，导致运行中的叶片气动外形与设计外形存在偏差，进而影响风力机气动性能[1−3]。叶片的气弹问题对风力机的影响逐步被发现和认识，因此研究叶片的气弹特性，对优化叶片设计和改进变桨控制具有重要意义[4−6]，很多学者就此作了大量研究。国内外文献中较多利用计算结构动力学(computational structural dynamics，CSD)与计算流体力学(computational fluid dynamics，CFD)耦合分析叶片气弹响应[7−11]，便于获取叶片位移，但求解精度依赖于流场建模策略、载荷与位移边界的施加方式，且计算量较大。此外，有学者研究了简化算法，HANSEN[12]利用有限梁元法建立了叶片气弹稳定性模型；陈严 等[13]以二节点梁单元对叶片离散化建模，分析了叶片在外形变化影响下的气弹特性；王旭东等[14]建立了风力机的气动耦合分析模型，研究了叶片的结构振动特性与来流风速的耦合效应；陈佳慧等[15]采用盒形梁理论耦合静气弹平衡方程计算了叶片结构变形。上述文献侧重于叶片弹性形变的计算研究，所述算法的难点在于计算惯性主轴的方向、弹性变形中心、剪切变形中心以及截面对于各惯性轴的抗弯或扭转刚度[16]，尤其对于结构和材料属性较为复杂的大型叶片，叶片上各截面的结构与材料参数难于准确计算。基于此，本文作者提出基于叶素动量理论(blade element momentum，BEM)的简化算法，通过推导叶片形变时气动载荷的修正模型，建立BEM与CSD双向耦合求解叶片形变与气动载荷，分析叶片形变对风力机气动性能的影响。

1 BEM模型

BEM广泛应用于叶片气动载荷计算和气动性能分析。引入BEM的改进模型计算叶片气动载荷，利用Prandtl模型[17]修正叶根损失和叶尖损失，利用叶栅理论[18]修正叶厚和叶宽引起的攻角改变量，并在轴向诱导因子较大时使用Buhl模型[19]进行修正。BEM模型中叶片微段的气动力和气动力矩如图1所示，其中，d为推力；dN为切向力；d为气动升力；d为气动阻力；db为俯仰力矩。

各气动力表达式为：

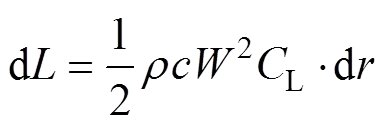
(2)

图1 作用于叶片微段的气动力

Fig. 1 Aerodynamic load on blade element

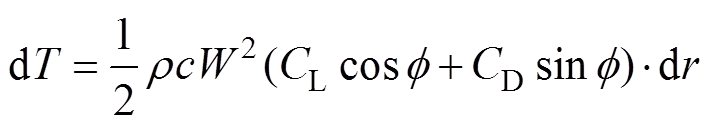
(4)

式中：为空气密度；为弦长；L为翼型升力系数；D为翼型阻力系数；为入流角；为气流相对速度。

俯仰力矩由叶素处翼型的俯仰力矩系数M决定，M表示翼型气动合力相对于1/4弦长处力矩的无因次系数[20]，则俯仰力矩为

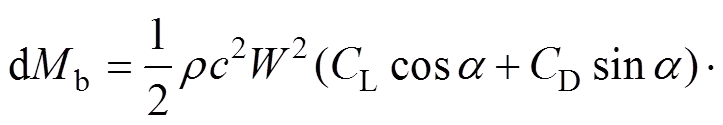
(5)

2 考虑叶片形变的气动载荷修正

叶片在载荷作用下产生的弹性形变，包括摆振和挥舞方向的弯矩作用下产生的展向弯曲及叶素内俯仰力矩作用下产生的扭转。而形变亦将改变叶片气动外形，影响叶片气动载荷。因此，为计算叶片在形变状态下的气动载荷，采用BEM求解作用于各叶素变桨轴心的气动载荷并转换到叶片坐标系，得到沿叶展分布的载荷集合后，在结构域中施加载荷，通过CSD计算得到各叶素形变量，并根据形变量对各叶素气动载荷进行修正，将新的载荷集合施加到叶片模型中重新求解形变量，直至形变量收敛则终止迭代。其过程包含2个方面：根据叶片位移计算各微段的形变量，根据叶片形变量重新计算气动载荷。

2.1 叶片微段形变量计算

微段处的形变量包含沿变桨轴的挠曲(以挠曲角度z表示)、绕变桨轴心的角位移(以扭转角度n表示)以及叶素平行位移，平行位移不影响叶素与气流的相对几何关系。

为计算叶素处扭转角度n与挠曲角度z，在叶素剖面设置如图2所示的3个参考点1，1，1。其中，1为剖面变桨中心；1为轴上参考点；1为轴上参考点。

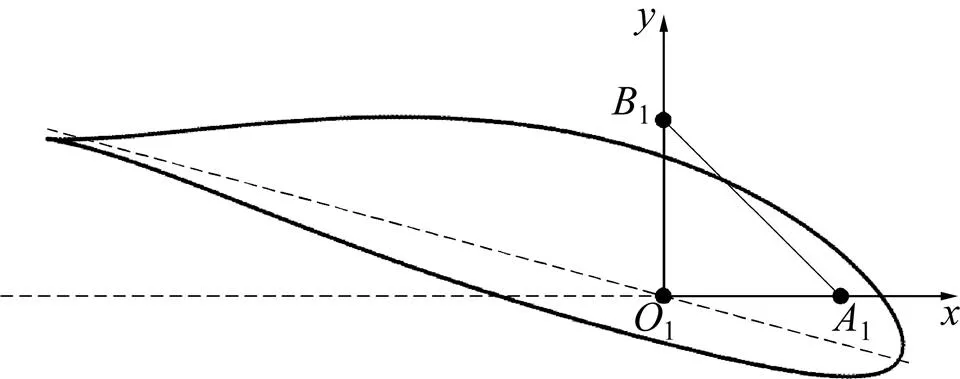
图2 叶片剖面参考点位置

图2中11平行于参考坐标系的轴即风轮周向，11平行于轴即风轮轴向。图3所示为对△111随叶片形变而发生位移过程的解析。

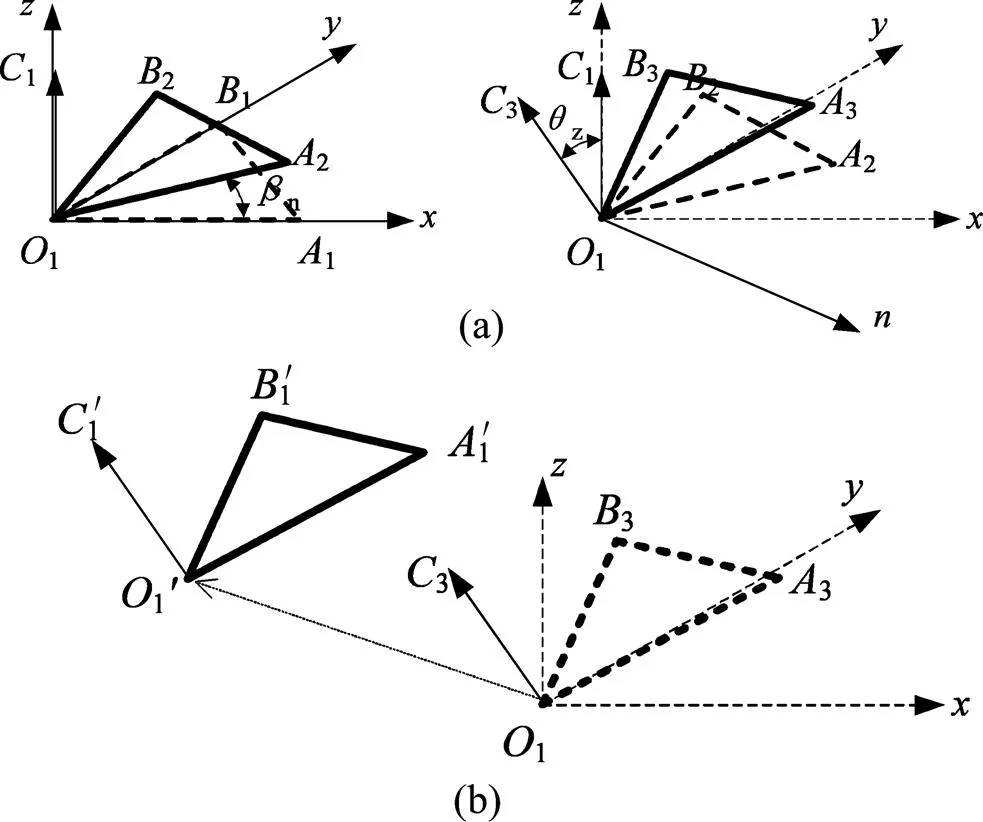
(a) 绕z轴的旋转与绕n轴的旋转过程；(b) 平移变换

图3中11、分别为位移前、后叶片剖面的法向量，轴垂直于11与13。形变前后参考点相对位置矩阵1和1′为：

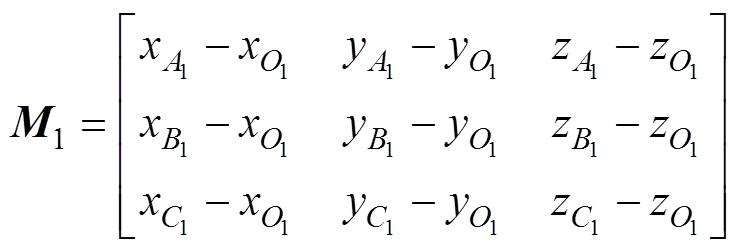
(7)

则图3所示的参考点位移过程表示为

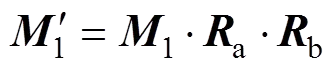
式中：a为绕轴旋转的变换矩阵，；b为绕轴旋转的变换矩阵，(其中为轴上单位向量)。

在CSD计算域中，通过有限元软件获取形变后叶片模型中所设参考点的坐标，利用式(8)求解叶素扭转角度n与挠曲角度z。

2.2 叶片微段气动载荷修正

令微段处修正后的气流周向、轴向气流速度分量分别为v′和v′，则有：

(10)

式中：为风轮转速；θ′为形变前后轴、′轴之间夹角(θ′，θ′，θ′等与此类同)；′为修正后的叶素−轮毂中心距离，(其中为叶展方向上该叶素微段序号)。

图4所示为经修正后叶素的气流速度三角形。

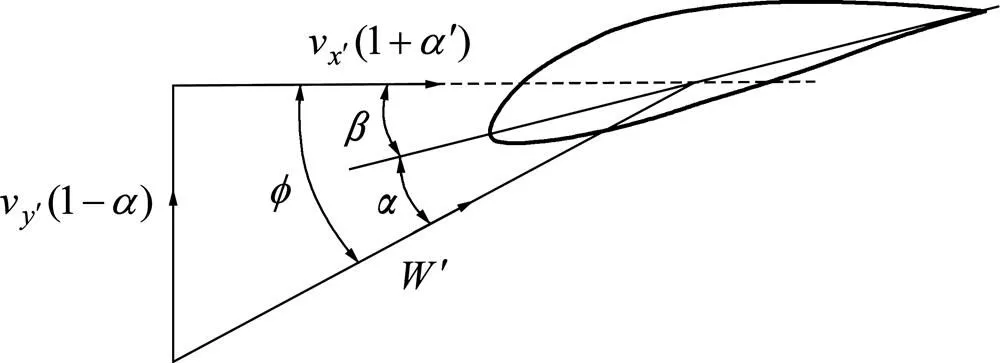
图4 修正后的气流速度

图4中为修正后的桨距角，

式中：0为安装角。

经修正后重新依据BEM模型计算气动载荷，所计算的d和dN平行于叶素剖面，db平行于剖面法向。为便于在叶片模型中加载，将重新计算的气动载荷转换至叶片坐标系，转换后气动力与气动力矩如式(12)~(17)所示。

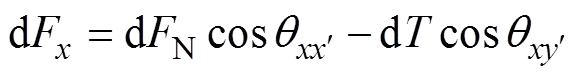
(13)

(14)

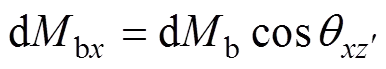
(16)

(17)

其中，dF和dbx平行于叶片坐标系轴，dF和dby平行于轴，dF和dbz平行于轴。

将式(12)~(17)所得集中载荷加载于CSD计算域叶片模型，计算当前载荷下的形变位移，代入式(8)计算对应形变量。

在上述形变计算与气动载荷计算之间建立双向耦合，设置迭代终止条件，则可求解对应工况下稳态的形变量和气动性能，由周向力分量dF沿叶展积分后，计算风力机风能利用系数P，

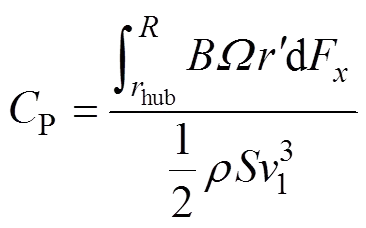
式中：hub为轮毂半径；为风轮半径；为风力机叶片数；为风轮扫掠面积。

3 叶片形变及其气动性能计算

针对某1 500 kW变速恒频风力发电机组叶片计算和分析，其中CSD计算部分使用ABAQUS软件。该机型额定风速13 m/s，风轮直径70 m，发电机额定转速1 800 r/min，其叶片使用AH系列翼型，内部为箱式梁结构。叶片的厚度远小于其长度，因此在ABAQUS中使用壳单元对叶片模型划分网格。

为保证模拟计算具有较好精度，沿模型展向共取402个截面，截面间距80~85 mm，在各截面上按图2所示的方式预设参考点，以各截面上的变桨轴心为点，即各微段集中载荷的受力点。

各工况下的形变计算中，设置相邻2次计算的P差值小于0.3%为迭代终止条件，计算了3~13 m/s风速时叶片在0°变桨角度下的形变。图5所示为8 m/s风速计算过程中各次迭代的形变量、周向力等主要 参数。

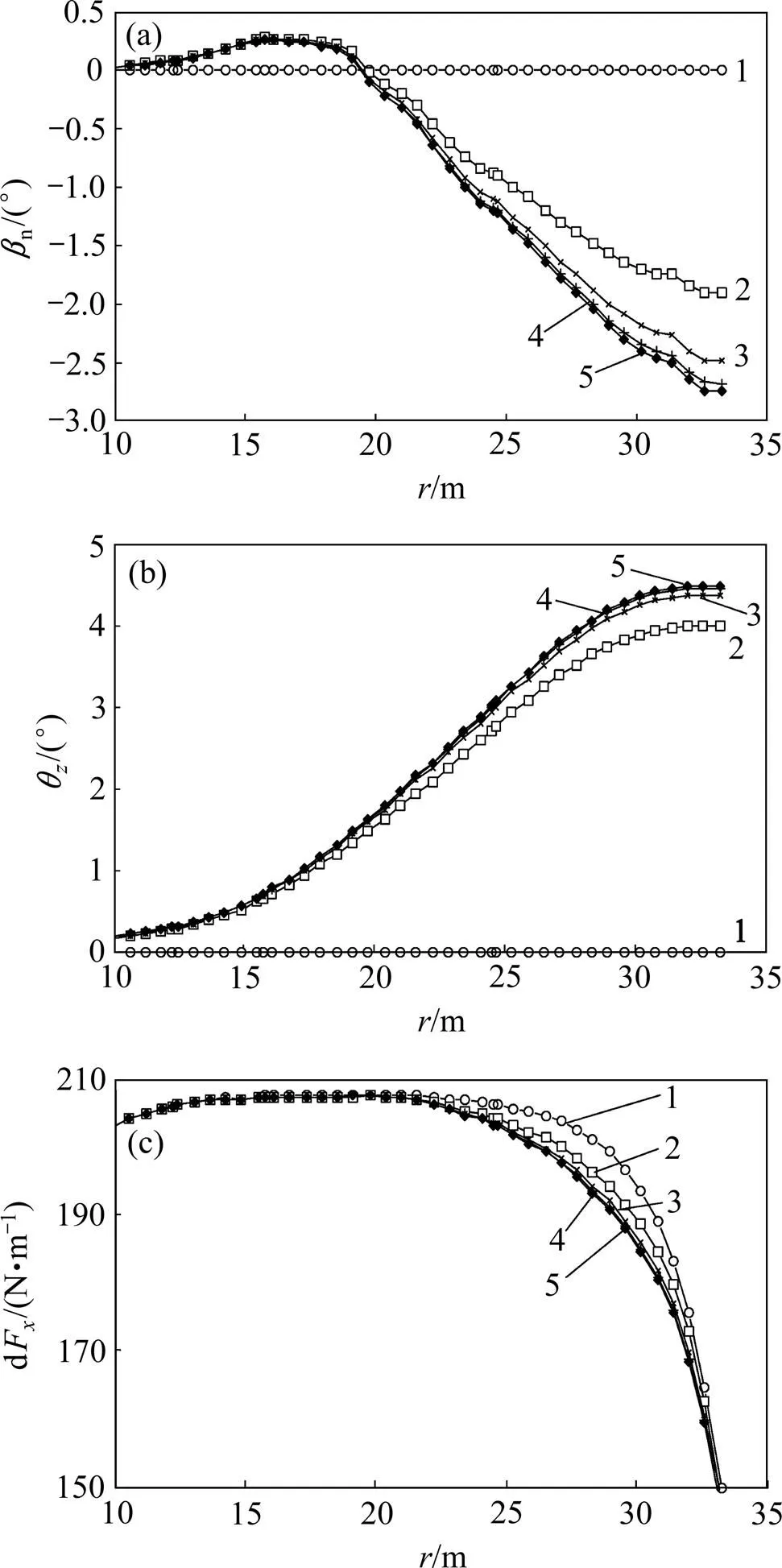
(a) 扭转角分布；(b) 挠曲角分布；(c) 周向力分布

由图5可知：代表形变程度的扭转角n、挠曲角z及代表气动性能的周向力dF在计算过程中均具备较好的收敛性，随迭代次数增加，沿叶展方向各参数趋于稳定，表示叶片形变与气动性能在双向耦合作用下趋于平衡。各风速对应计算历经3~5次迭代完成，具有较高效率。

为进一步分析各风速下运行的叶片发生形变的特性，提取各风速对应的稳态形变量参数扭转角n、挠曲角z沿展向分布情况，如图6所示。

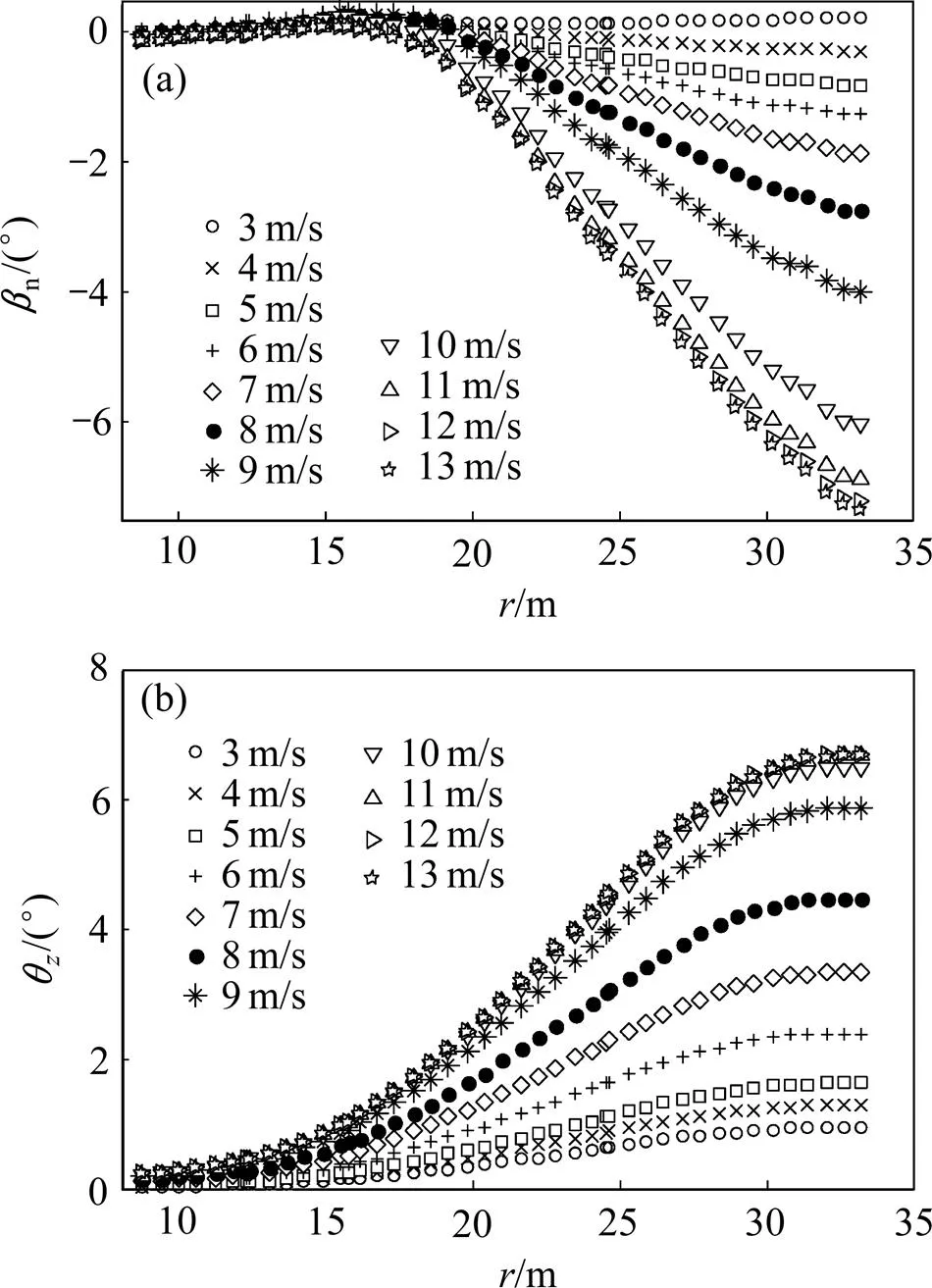
(a) 扭转角沿展向分布；(b)挠曲角沿展向分布

由图6(a)可知：挠曲角沿叶展的分布及变化趋势，在叶根及叶片前段因气动载荷较小、翼型厚度与材料厚度较大，其挠曲程度较小；叶片中段部分气动载荷较大，而翼型厚度与材料厚度相对前段减小，因而挠曲程度逐渐增大，在叶展长60%~70%附近挠曲变化加快，表示该段发生挠曲形变后曲率较大；叶片后段接近叶尖处气动载荷较小，致挠曲程度逐渐收敛。在3~13 m/s各风速下叶片挠曲角变化趋势相似，整体上随着风速增大、气动载荷增加，挠曲形变程度随之 增大。

由图6(b)可知：扭转角沿叶展的分布与变化趋势，与挠曲角变化趋势类似，在各风速下叶片沿展向的扭转程度单调增大，较为不同的是在叶片后段气动载荷及翼型气动中心与变桨轴心相对距离的影响下，各风速下的扭转角变化率极值点相对靠近后段。在3~4 m/s风速下，叶片整体扭转形变程度接近0°，5~11 m/s风速下，叶片扭转形变加剧。

此外，由图6可见，在叶片中后段各微段呈0°~6°的挠曲形变及0°~5°的扭转形变，将直接影响风力机轴向力矩，造成风力机P偏离初始设计时的最大值，可视为叶片形变造成叶片整体产生了一定攻角差值，为量化这一影响，本文定义修正角Δ，表示对叶片攻角偏差的补偿，并将式(11)修正为

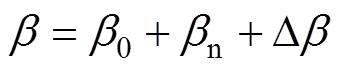
将式(19)代入计算模型，计算形变状态下该风力机风能利用系数，图7所示为考虑叶片形变时的P−1−Δ关系。

(a) 采用不同修正角的1−P曲线；(b)最佳P对应的1−Δ关系

图7 考虑叶片形变时的P−1−Δ关系

Fig. 7 Relationship ofP−1−Δconsidering deformation of blade

由图7(a)可见：不同修正角作用下，最佳P覆盖的风速区间小于设计范围5~9 m/s，在设计工况下运行时(如图7(b)中曲线1所示)，该风力机仅在5~7 m/s风速范围内具有较好的P，沿曲线1运行时风力机已不具备初始设计的气动性能。

此外，由图7(b)可知：对叶片施加一定的修正角Δ，可使得风力机在更大风速区间内具备较好的P，其中曲线2代表了各风速下最佳P所对应的修正角，显示该风力机沿曲线2运行时可在各风速下追踪最佳P，在5~9 m/s风速范围内修正角取值为0.75°~1.50°，可视为在该风速范围内叶片形变产生了−1.50°~−0.75°的等效攻角偏差。

图8所示为该叶片在上述2种工况及刚性假设时的P曲线对比情况。

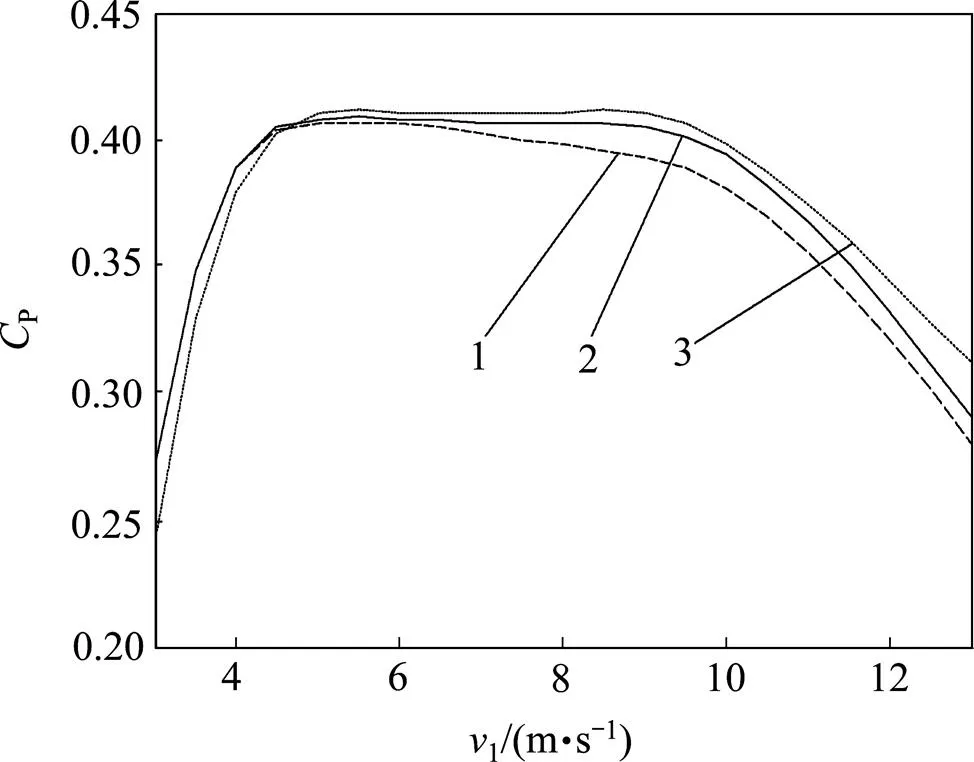
1—曲线1，Δβ=0°，优化前的实际运行情况；2—曲线2，CP=CPmax，优化后的实际运行情况；3—曲线3，Δβ=0°，设计运行情况。

图8中，曲线1与2所示工况分别对应于图7(b)中曲线1与曲线2的工况，曲线3表示叶片刚性假设时在设计运行工况下的P曲线，为初始设计的理论P曲线。由图8可见：计及叶片形变时风力机P在5~13 m/s范围内低于设计值，施加图7(b)中曲线2所示的修正角后，使得该风速段内P得以部分补偿。

4 结论

1) 本文建立的叶片形变量计算、气动载荷修正模型，较准确地量化风力机叶片在不同风速下的弹性形变，具备较高的计算效率。

2) 在变速运行阶段、功率爬升阶段，风力机气动性能低于叶片刚性假设下的设计值，说明叶片形变对于风力机风能捕捉能力存在负面影响。

3) 通过计算叶片形变所产生的等效攻角偏差，对叶片施加相应的修正角，可部分抑制叶片形变的影响，使风力机气动性能损失得以一定的补偿。

4) 本文的计算模型可较快计算叶片在不同风速下的弹性形变，可用于叶片气动外形与结构设计的修正，从而优化叶片设计，同时，计算不同风速下的叶片等效攻角差值及其补偿角，可用于优化风力发电机组变桨控制算法。

[1] LEE Y J, JHAN Y T, CHUNG C H. Fluid-structure interaction of FRP wind turbine blades under aerodynamic effect[J]. Composites Part B: Engineering, 2012, 43(5): 2180−2191.

[2] HANSEN M O L. Aerodynamics of wind turbines[M]. London: Routledge, 2015: 110−136.

[3] HANSEN M O L, SØRENSEN J N, VOUTSINAS S, et al. State of the art in wind turbine aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences, 2006, 42(4): 285−330.

[4] BARLAS T K, WINGERDEN W, HULSKAMP A W, et al. Smart dynamic rotor control using active flaps on a small-scale wind turbine: aeroelastic modeling and comparison with wind tunnel measurements[J]. Wind Energy, 2013, 16(8): 1287−1301.

[5] HOOGEDOORN E, JACOBS G B, BEYENE A. Aero-elastic behavior of a flexible blade for wind turbine application: a 2D computational study[J]. Energy, 2010, 35(2): 778−785.

[6] CAPUZZI M, PIRRERA A, WEAVER P M. A novel adaptive blade concept for large-scale wind turbines, Part I: aeroelastic behaviour[J]. Energy, 2014, 73: 15−24.

[7] GUO T Q, LU Z L, TANG D, et al. A CFD/CSD model for aeroelastic calculations of large-scale wind turbines[J]. Science China Technological Sciences, 2013, 56(1): 205−211.

[8] BAZILEVS Y, HSU M C, KIENDL J, et al. 3D simulation of wind turbine rotors at full scale. Part Ⅱ: fluid-structure interaction modeling with composite blades[J]. International Journal for Numerical Methods in Fluids, 2011, 65(1/2/3): 236−253.

[9] YU D O, KWON O J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD–CSD method[J]. Renewable Energy, 2014, 70: 184−196.

[10] 胡丹梅, 张志超, 孙凯, 等. 风力机叶片流固耦合计算分析[J]. 中国电机工程学报, 2013, 33(17): 98−104.HU Danmei, ZHANG Zhichao, SUN Kai, et al. Computational analysis of wind turbine blades based on fluid-structure interaction[J]. Proceedings of the CSEE, 2013, 33(17): 98−104.

[11] CARRIÓN M, STEIJL R, WOODGATE M, et al. Aeroelastic analysis of wind turbines using a tightly coupled CFD–CSD method[J]. Journal of Fluids & Structures, 2014, 50: 392−415.

[12] HANSEN M H. Aeroelastic stability analysis of wind turbines using an eigenvalue approach[J]. Wind Energy, 2004, 7(2): 133−143.

[13] 陈严, 方郁锋, 刘雄, 等. 考虑风力机叶片截面扭转运动及外形变化的气动弹性分析[J]. 太阳能学报, 2014, 35(4): 553−561.CHEN Yan, FANG Yufeng, LIU Xiong, et al. Aeroelastic analysis on section twist and shape change of wind turbine blade[J]. Acta Energiae Solaris Sinica, 2014, 35(4): 553−561.

[14] 王旭东, 陈进, 张石强. 基于气动弹性理论的风力机叶片耦合分析[J]. 太阳能学报, 2010, 31(1): 96−100. WANG Xudong, CHEN Jin, ZHANG Shiqiang. Coupling analysis of wind turbine blades based on aeroelastics and aerodynamics[J]. Acta Energiae Solaris Sinica, 2010, 31(1): 96−100.

[15] 陈佳慧, 王同光. 考虑气动弹性的风力机叶片性能分析[J]. 空气动力学学报, 2011, 29(3): 396−400. CHEN Jiahui, WANG Tongguang. Wind turbine performance analysis with aeroelastic effect[J]. Acta Aerodynamica Sinica, 2011, 29(3): 396−400.

[16] 汪泉, 陈进, 程江涛, 等. 风力机叶片二元翼段静气动弹性机理[J]. 沈阳工业大学学报, 2012, 34(6): 623−628. WANG Quan, CHEN Jin, CHENG Jiangtao, et al. Static aeroelastic mechanism of two dimensional airfoil section for wind turbine blade[J]. Journal of Shenyang University of Technology, 2012, 34(6): 623−628.

[17] SILVESTRE F J, LUCKNER R. Experimental validation of a flight simulation model for slightly flexible aircraft[J]. AIAA Journal, 2015, 53(12): 3620−3636.

[18] SØRENSEN J N. Aerodynamic aspects of wind energy conversion[J]. Annual Review of Fluid Mechanics, 2011, 43: 427−448.

[19] BUHL M L. A new empirical relationship between thrust coefficient and induction factor for the turbulent windmill state[M]. Golden, CO: National Renewable Energy Laboratory, 2005: 1−7.

[20] DRELA M. XFOIL: An analysis and design system for low Reynolds number airfoils[M]. Heidelberg: Springer, 1989: 1−12.

(编辑 赵俊)

Aeroelastic deformation and aerodynamic performance of wind turbine blades based on BEM

HE Jia1, 2, XIAO Yang1, DENG Youhan3, WU Shijing1

(1. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China;2. Lichuan Wind Power Co. Ltd, China Three Gorges New Energy Co. Ltd., Lichuan 445400, China;3. Three Gorges Power Plant, China Yangtze Power Co. Ltd., Yichang 443000, China)

To study the blade deformation influence on the aerodynamic performance of wind turbine, analytical method of blade deformation and aerodynamic performance based on modified Blade Element Momentum theory was proposed. A deformation calculation and aerodynamic load modifying model was constructed for blades with elastic deformation, which is iteratively solved by modified Blade Element Momentum theory coupling with computational structural Dynamics. Taking 1500 kW wind turbine blade as an example, effect law of elastic blade deformation affecting the aerodynamic performance under different wind velocity was obtained. The results show that the calculation mode can quantify elastic deformation of blade with different wind speed quickly, and can be used for modifying aerodynamic shape of blade and structural design and then optimize the design of blade. Through calculating elastic deformation of blade with different wind speed, it can be used for optimizing pitch control algorithm of wind generating set.

blades of wind turbines; aeroelastic; coupling analysis; torsion angle; flexural angle; aerodynamic performance

10.11817/j.issn.1672-7207.2017.09.033

TK83

A

1672−7207(2017)09−2513−07

2016−09−23；

2016−12−05

国家自然科学基金资助项目(51375350) (Projects(51375350) supported by the National Natural Science Foundation of China)

巫世晶，教授，博士生导师，从事风能利用及风力机械方面的研究；E-mail: wsj@whu.edu.cn