考虑温度与时变因素耦合的混凝土桥梁增量分析方法

林鸣，付宏渊，颜东煌



考虑温度与时变因素耦合的混凝土桥梁增量分析方法

林鸣1, 2，付宏渊1，颜东煌1

(1. 长沙理工大学土木与建筑学院，湖南长沙，410114；2. 湖南省交通规划勘察设计院有限公司，湖南长沙，410008)

为了准确掌握在材料时变特性因素(如混凝土弹性模量、收缩徐变、预应力钢筋松弛等)与温度变化耦合作用下混凝土桥梁施工期及运营期结构效应变化历史，基于时间序列划分，采用增量形式的虚功平衡方程，推导考虑温度变化与材料时变因素耦合的有限元求解方程；结合具体时变函数表达，建立考虑温度耦合作用时混凝土时变弹性模量修正公式及时间增量步内一维梁单元计入时变因素影响的杆端荷载项表达式。结合实际工程，采用所提出的计算方法进行编程计算，将考虑温度耦合作用的计算结果与不考虑温度耦合作用的计算结果及实测结果进行对比分析。研究结果表明：考虑温度耦合作用的长期挠度计算结果与实测结果更接近，说明考虑温度与时变特性耦合效应的增量分析计算方法能有效提高混凝土桥梁计算分析的准确性和可靠性。

桥梁工程；收缩徐变；增量分析方法；混凝土桥梁；应力松弛

在混凝土结构中，混凝土弹性模量、混凝土的徐变、混凝土的收缩等时变因素对结构的长期挠度和受力状态影响显著[1]，而温度变化对徐变等时变因素的影响不能忽略[2]；目前，混凝土时变函数的B3模型和CEB-FIB2010模型[3−4]均给出了温度变化情况下时变因素函数修正方法。在大跨混凝土桥梁结构分析方法中，能够考虑材料时变因素影响的方法主要有4种，其中有效弹性模量法是一种简化方法，可将徐变非线性本构关系转换为线性表达关系，简单有效，但计算精度较低[5−6]；有限元全量分析方法可准确考虑徐变柔度、多次加载等因素，计算精度较高，但难以考虑温度变化的耦合效应影响[7−8]；有限元增量分析方法符合混凝土时变因素具有依赖应力应变历史的非线性特性，可有效考虑各种耦合效应，是理论上较完备的分析方法[9−13]。BAZANT等[14−15]提出了一种基于ABAQUS软件、利用用户子程序界面修改各时变因素参数取值并进行增量分析的计算方法，取得了良好的分析效果，但这一方法对使用者的理论水平要求较高，不便于推广。目前针对大跨混凝土桥梁，缺少一种能充分考虑混凝土弹性模量的时变效应并计入温度变化对混凝土时变因素影响相耦合的可直接编程的具体分析方法。为解决这一问题，作者基于时间序列划分，采用考虑几何非线性的UL格式的虚功增量方程，推导在实际季节温度场变化情况下计入混凝土材料时变因素影响的有限元求解方程，得出在时间增量步内，杆系单元计入混凝土的徐变、收缩以及预应力筋的应力松弛影响的杆端荷载项公式，给出考虑温度变化耦合效应的具体修正公式，并给出具体增量步内进行温度与时变因素耦合效应计算分析的程序框图。利用编制的计算程序，在具体工程项目中进行应用，以验证计算方法的精度和可靠性。

1 计算分析方法

1.1 基本假定

本文中的推导和分析基于如下基本假定：1) 应力与应变在时间段内增量间满足线性关系；2) 混凝土工作应力小于0.4倍极限抗压强度，不出现完全卸载，徐变应变适用线性叠加原理[4]；3) 符合大变形小应变假定；4) 作用温度范围为−20~80 ℃。

1.2 增量求解方程

根据分析要求，将混凝土桥梁按施工阶段和运营阶段时间历程顺序分为∆1，…，∆t，∆t+1等时间段，由虚位移原理，采用UL格式，可得出考虑几何非线性的t+∆t+1时刻的增量平衡方程[16]：

(1)

式中：变量的左下标表示变量值开始的时刻，左上标表示变量值终止的时刻；S，，，和分别表示应力张量、格林应变张量、体积力、边界力和位移。表示微分算子，表示体积积分，表示面积积分。

计入温度耦合效应的混凝土徐变理论中，∆t+1时段内应变增量可采用如下公式表达[17]：

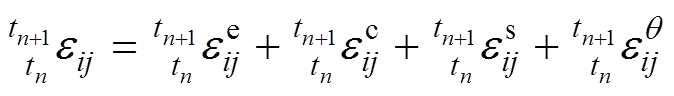
式中：右上标e表示弹性；c表示徐变作用；s表示收缩作用；为温度。

同时，根据式(2)和基本假定(1)，则应力增量可表示为

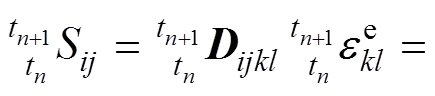
(3)

其中表示t时的材料弹性矩阵。根据格林应变张量的位移表达式，则可得到应变增量的分解表达式：

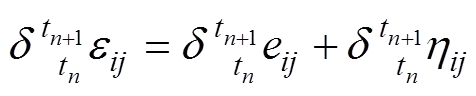
式中：e和η分别为位移增量u的线性项和二次项。将式(3)和(4)代入式(1)，整理后可推导出

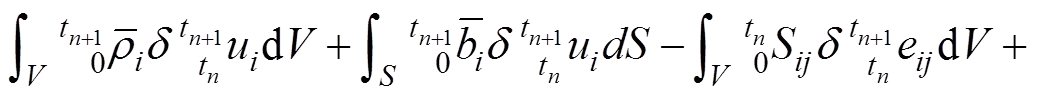
(5)

定义插值矩阵，则单元内位移增量u可由节点位移增量插值而来，即

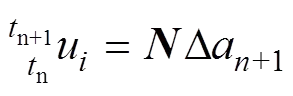
由应变−位移关系，可推导出单元应变增量和节点位移增量间的关系表达式：

式(7)中L表示拉普拉斯算子。将式(6)和(7)代入式(4)，忽略位移函数的二次项，可推导出增量形式的有限元求解方程：

(8)

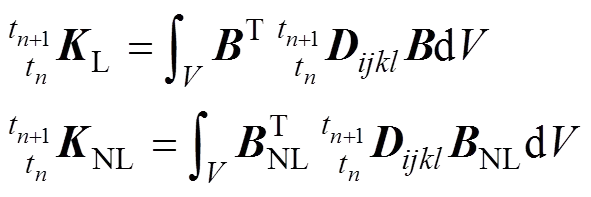
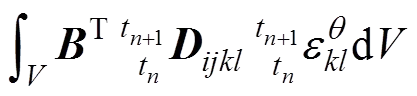
(11)

式中：L为弹性刚度矩阵；NL为初应力矩阵；为不平衡力向量；w为外荷载向量；l为内力向量；为应变矩阵。

式(8)在外荷载向量中加入了考虑混凝土材料时变因素作用和温度作用的虚拟荷载项。

1.3 弹性模量时变效应

混凝土材料的弹性模量会随时间发生明显的非线性变化，在精细化的大跨混凝土桥梁分析中有必要考虑其时变效应。

为计入其时变效应，式(10)中，要在每一时间段内计算初始的弹性模量c(t)，由此进行弹性矩阵的修正。c(t)宜采用CEB-FIP2010给出的时变函数表达式[4]：

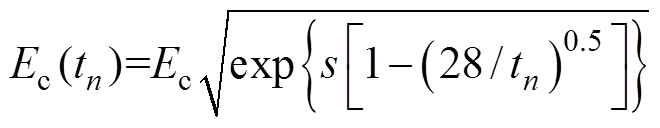
式中：c为混凝土试块28 d的实测弹性模量(测试温度为20 ℃)；为采用不同水泥型号时的影响系数。

1.4 混凝土徐变时变作用

根据CEB-FIP2010中关于多次加载情况下的徐变应变线性累积假定，则∆t+1时间步内徐变应变增量可表示为

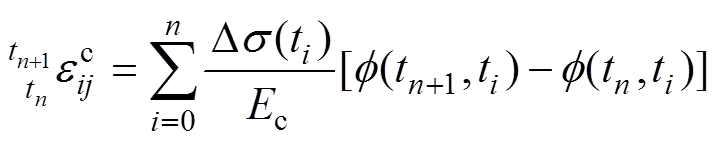
式中：(t, t)为混凝土的徐变系数；为∆t时间段内施加的荷载产生的截面应力。

在一维梁单元中，可用∆t+1时间段内的弹性模量c(t)代替弹性矩阵，则式(10)中的混凝土徐变作用部分可改写为

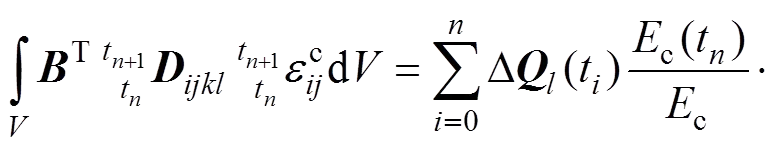
(14)

式(14)表明：徐变作用效应可表达为各主要外荷载的作用效应增量的函数。

1.5 混凝土收缩时变作用

由CEB-FIP2010给出的收缩应变关系式，推导出∆t+1增量步内的收缩应变增量：

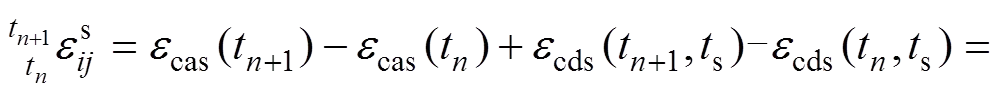
(15)

式中：cas和cds分别为混凝土的自收缩应变函数和干燥收缩应变函数；cs为混凝土的收缩系数；s为混凝土收缩开始时间。将式(15)代入式(10)，在一般情况下，对于一维杆系单元，收缩应变沿截面高度的分布是均匀的，因此，混凝土时变收缩作用可由单元轴向节点力表示[18]，由此推导出计入收缩作用的杆端力公式为

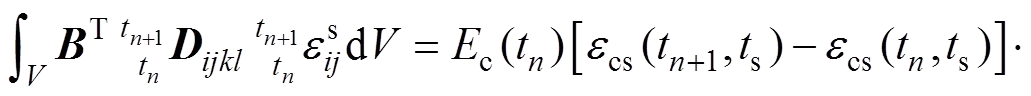
(16)

式中：为单元的截面面积。式(16)表明：时间步内的收缩作用可由负单元杆端轴力计入。

1.6 温度作用

当符合基本假定第4条时，可认为温度变化引起的温度应变增量为线性，可以表示为

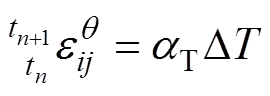
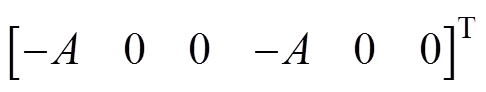
式(18)表明：增量步内的均匀温度场变化作用效应可由单元杆端轴力表达。

1.7 温度变化耦合作用

温度变化除引起温度应变外，还会引起混凝土桥梁的各种材料时变参数的变化。

根据CEB-FIP2010中的温度相关影响函数，温度对混凝土弹性模量的影响可表达为

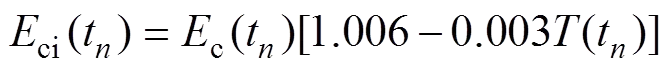
式中：ci(t)为经过温度修正后的有效弹性模量；(t)为∆t+1时间步内的平均温度。

目前，常用的收缩徐变模型都是在20 ℃恒温条件下的试验数据基础上拟合得到，因此，在平均温度变化条件下，需要对徐变和收缩模型进行修正：

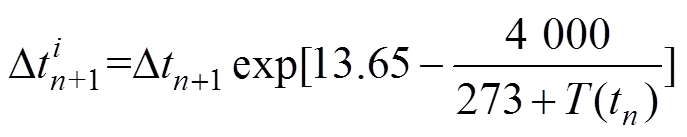
式(20)为当平均温度不是20 ℃时，进行收缩徐变应变计算时采用的修正时间增量步长计算公式。同时，公式(13)和(15)中的徐变系数公式和收缩应变函数公式也需要根据CEB-FIP2010中相关规定予以修正。

1.8 预应力索松弛作用

在大跨混凝土桥梁中，往往设计大量的体内和体外预应力索，而预应力索的时变应力松弛必须在计算中予以计入。

由文献[18]和文献[19]推荐的预应力钢索应力松弛函数，可将∆t1时间段内钢索应力松弛产生的作用表达为

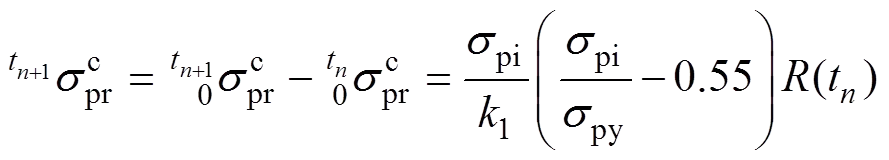
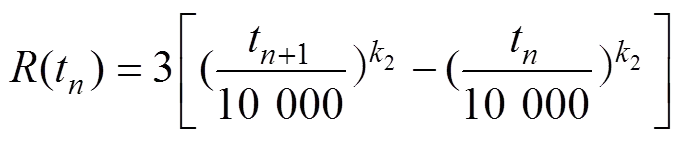
在结构计算分析中，预应力索可模拟为分段杆单元，则∆t+1时间段内预应力索应力松弛作用产生的杆端力增量为

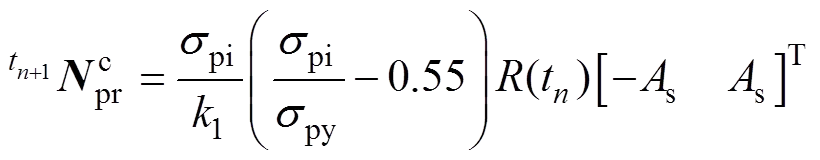
其中：s为预应力钢筋截面面积。

2 计算程序框图

在不考虑混凝土材料进入弹塑性状态情况下，以上计算分析方法属于考虑几何非线性的增量分析方法。为了便于进一步理解具体的程序分析计算的详细流程，给出1个时间增量步内计算分析的具体程序框图，见图1。

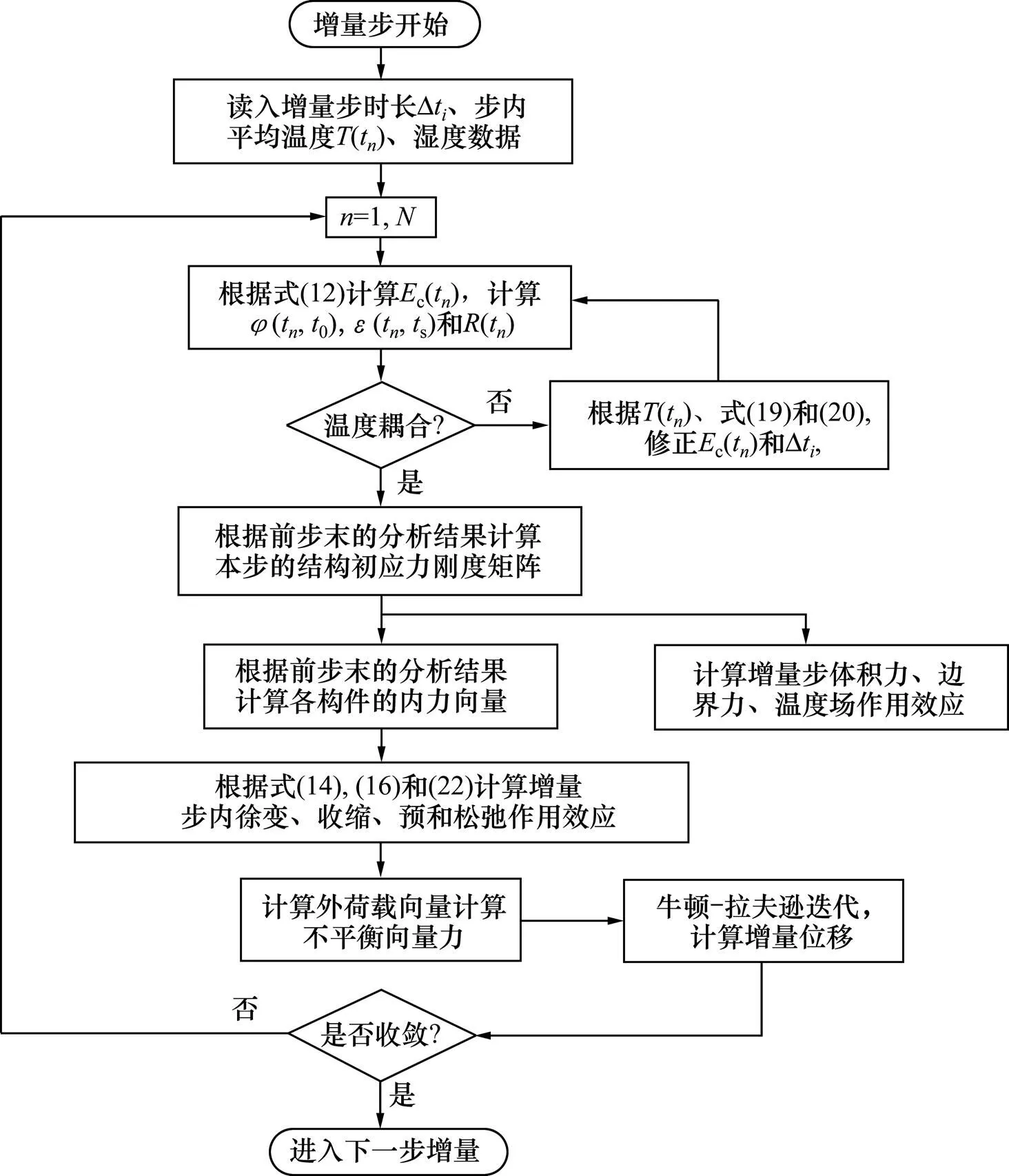
图1 增量步内程序流程

3 实际工程应用

3.1 工程简介

湘江银盆岭大桥是我国早期建设的单索面双塔混凝土斜拉桥，桥型布置如图2所示。混凝土主梁为单箱三室预应力箱梁，箱梁高度为3.4 m。扇形索面，东、西索塔每塔左右对称各布置15对斜拉索；混凝土主梁上纵桥向索距为6.2 m，上、下游拉索横桥向间距为2.4 m。

银盆岭大桥建成21 a后，于2012−10完成全桥加固维修施工。

3.2 主梁长期挠度变化分析

根据本文给出的计算方法进行编程，有针对性地计算湘江银盆岭大桥的主梁长期挠曲变形，计算工况如下。

1) 以1990−12“湘江银盆岭大桥主桥静动力试验报告”中提供的主梁线形和成桥索力为基础条件，考虑施工期的工序时间和加载顺序，建立桥梁计算的初态模型。

2) 以施工期构件施工完成时间作为初始加载时间0；主塔墩以1989−02开始分段计入；加劲梁从1989−12起，依次按每悬拼节段(3.1 m)施工期为10 d进行计算。

3) 运营期时间序列划分：从1991−01起，每3月作为1个时间增量步，时间段内平均温度和湿度根据桥位所在的开福区气象局的资料取值，截至2010−09共分为79个计算时间段。

本文分析结果及Midas Civil分析结果与1998年，2002年和2010年测试的成桥时的相对主梁挠度实测结果(表中结果均已修正温度场影响及历次桥面维修导致的超重影响)进行比较，如表1所示。主梁跨中长期挠曲变形分析值与实测值比较见表2。

从表1可以看出：由于Midas Civil软件计算结果未考虑混凝土弹性模量的时变效应和预应力筋松弛的影响，其计算得到的长期挠度分析值明显偏小；考虑各类混凝土时变因素影响的本文方法1其分析结果要好于Midas Civil分析结果，但计算的长期挠度分析值仍偏小；而采用考虑温度与时变因素耦合效应的本文方法2时，由于修正了温度对计算时间步长及时变函数的影响，计算的长期挠度分析结果明显更加接近实测值，分析的可靠性要比不考虑耦合效应的本文方法1高。

单位：m

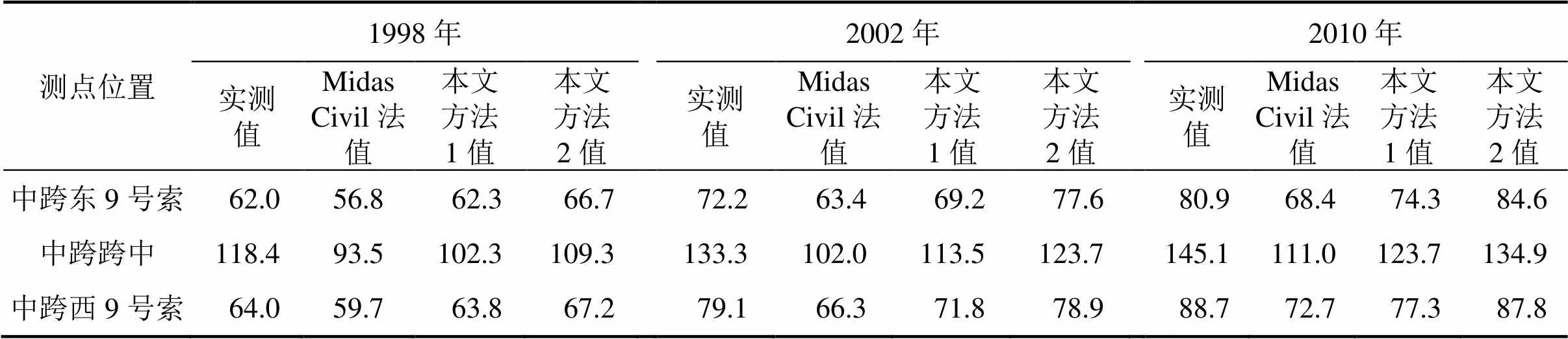
表1 主梁长期挠曲变形分析值与测试值的比较

注：Midas Civil法中收缩徐变采用CEB-FIB90模型，不考虑温度耦合作用；本文方法1考虑混凝土弹性模量、徐变收缩及预应力筋松弛时变模型，但不考虑温度与时变因素耦合作用；本文方法2分析则考虑温度与时变因素耦合作用。

表2 主梁跨中长期挠曲变形分析值与实测值比较

从表2可见：不考虑温度与时变因素耦合作用时，本文方法1的计算分析结果与Midas Civil分析结果差异不大；而考虑温度与时变因素耦合作用的本文方法2计算结果则与实测值更吻合，与本文方法1所得计算精度相比提高约15%。

3.3 主梁相对线形变化

从2010−09到2011−08，对银盆岭大桥换索前的桥跨结构状态进行连续监测(每月2次)，利用本文计算方法编制的分析程序，对监测期主梁相对线形变化情况进行计算。

1) 以2010−09的桥跨结构分析状态为初始值，分析监测期间典型温度场变化下的主梁相对线形变化情况。

2) 分析期间时间序列划分。从2010−09开始，每15 d为1个时间增量步，增量步内平均温度和湿度按监测期实测取值，截止2011−08共分为21个计算时间段。

3) 监测测试时间选择在凌晨3:00到4:00车流量极小时段，此时，各桥梁构件温度变化基本稳定，假设构件为均匀温度场。

监测期间桥梁典型温度测试结果如表3所示。

本文分析结果及Midas Civil分析结果与实测的主梁相对线形变化结果进行比较，如表4所示。

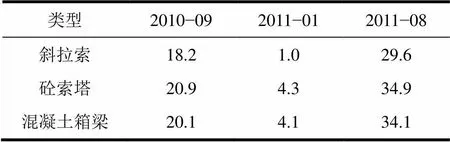
表3 监测期间的桥梁典型温度场

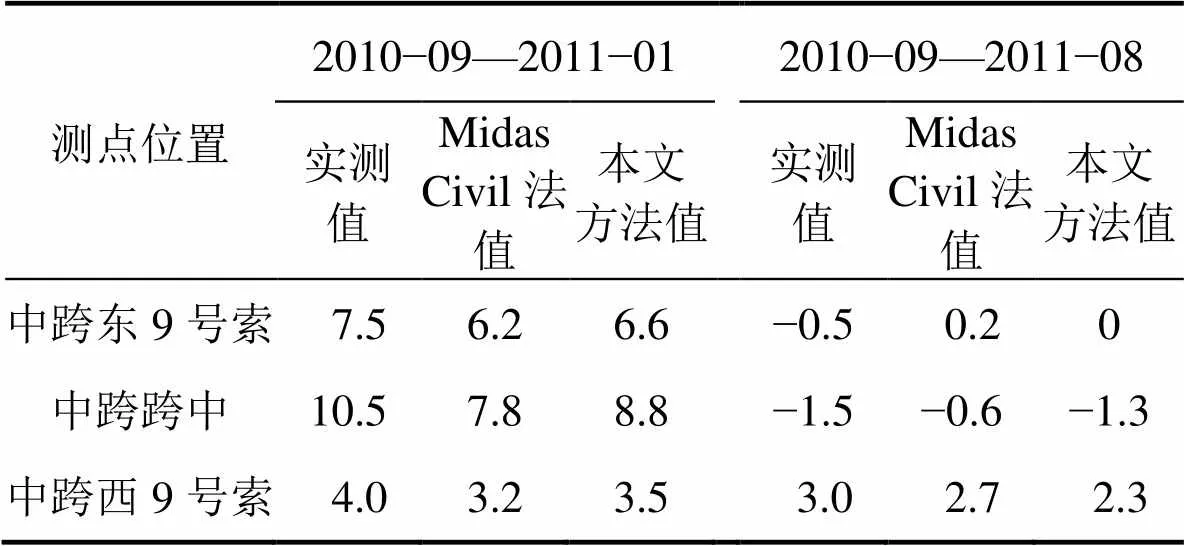
表4 主梁相对线形变化分析值与实测值的比较

注：Midas中收缩徐变采用CEB-FIB90模型，不考虑温度耦合作用；本文分析中考虑温度耦合作用。

从表4可以看出：由于混凝土收缩徐变基本完成，同时分析周期较短，考虑耦合效应对计算时间步长和时变函数修正产生的影响较小，Midas Civil分析结果与本文分析结果基本相同；但考虑温度对弹性模量影响的耦合效应，仍使本文分析结果与Midas Civil分析结果产生一定差异，与Midas Civil分析结果相比，与实测值更接近。

4 结论

1) 基于时间历程划分，推导了可考虑温度与混凝土时变因素耦合作用效应的几何非线性增量有限元求解方程，进一步完善了大跨混凝土桥梁长期作用效应分析的计算方法。

2) 给出1个时间增量步内计算分析的具体程序框图，并编制了计算程序，程序计算结果与实测值较吻合，验证了程序的准确性。

3) 对于大跨混凝土桥梁，在进行运营期桥跨结构状态分析时，考虑温度与混凝土弹性模量的耦合作用效应可以提高分析结果的精确性和可靠性。

[1] LIU Yangjun. Strength, modulus of elasticity, shrinkage and creep of concrete[D]. Florida: University of Florida. Civil and Coastal Engineering Department, 2007: 22−55.

[2] BAZANT Z, CUSATIS G, CEDOLIN L. Temperature effect on concrete creep modeled by microprestress-solidification theory[J]. Journal of Engineering Mechanics, 2004, 130(6): 691−699.

[3] BAZANT Z, BAWEJA S. Creep and shrinkage prediction model for analysis and design of concrete structures: model B3[R]. Illinois: Northwestern University. The American Center for Biological Medicine, 1995: 1−77.

[4] FIP Model Code 2010, CEB/FIB model code for concrete structure[S].

[5] DILGER W H. Creep analysis of prestressed concrete members using creep transformed section properties[J]. ACI Journal, 1982, 79(1): 98−117.

[6] 刘婷, 薛伟辰, 王巍. 全预应力混凝土梁长期变形计算[J]. 工程力学, 2016, 33(9): 116−122.LIU Ting, XUE Weichen, WANG Wei. Calculation on long-term deflections of fully prestressed concrete beams[J]. Engineering Mechanics, 2016, 33(9): 116−122.

[7] 胡狄, 陈政清. 预应力混凝土桥梁徐变分析的全量形式自动递进法[J]. 工程力学, 2004, 21(5): 41−45. HU Di, CHEN Zhengqing. Automatically step-up method for creep analysis of prestressed concrete bridges[J]. Engineering Mechanics, 2004, 21(5): 41−45.

[8] 高政国, 黄达海, 赵国藩. 混凝土结构徐变应力分析的全量方法[J]. 土木工程学报, 2001, 34(4): 10−14.GAO Zhenguo, HUANG Dahai, ZHAO Guofan. A method for creep stress analysis of concrete structure[J]. China Civil Engineering Journal, 2001, 34(4): 10−14.

[9] JURKIEWIEZA B, DESTREBECQB J F, VERGNE A. Incremental analysis of time-dependent effects in composite structures[J]. Computers and Structures, 1999, 73(1): 425−435.

[10] 陈常松, 颜东煌, 李学文. 混凝土收缩徐变分析的虚功增量方程及应用[J]. 工程力学, 2010, 27(10): 139−144. CHEN Changsong, YAN Donghuang, LI Xuewen. The Incremental virtual work equation for concrete shrinkage and creep analysis and its applications[J]. Engineering Mechanics, 2010, 27(10): 139−144.

[11] ATES S. Numerical modelling of continuous concrete box girder bridges considering construction stages[J]. Applied Mathematical Modelling, 2011, 35(8): 3809−3820.

[12] FRANCIS T K, SI X T. Time-dependent effects on dynamic properties of cable-stayed bridges[J]. Structural Engineering and Mechanics, 2012, 41(1): 139−155.

[13] 邓继华, 邵旭东, 彭建新. 几何非线性平面梁考虑收缩徐变的算法研究[J]. 湖南大学学报(自然科学版), 2014, 41(9): 14−19. DENG Jihua, SHAO Xudong, PENG Jianxing. Algorithm study of the geometrical nonlinearity plane beam considering creep and shrinkage[J]. Journal of Hunan University (Science and Technology), 2014, 41(9): 14−19.

[14] BAZANT Z P, YU Qiang, LI Guanghua. Excessive long time deflections of prestressed box girders: Ⅰ. record-span bridge in Palau and other paradigms[J]. Journal of Structural Engineering, 2012, 138 (6): 676−686.

[15] BAZANT Z P, YU Qiang, LI Guanghua. Excessive long time deflections of prestressed box girders: Ⅱ. numerical analysis and lessons learned[J]. Journal of Structural Engineering, 2012, 138 (6): 687−695.

[16] 王勖成, 邵敏. 有限单元法基本原理和数值方法[M]. 2版. 北京: 清华大学出版社, 1997: 491−511. WANG Xucheng, SHAO Min. Basic principle of finite element method and numerical method[M]. 2nd ed. Beijing: Tsinghua University Press, 1997: 491−511.

[17] BAZANT Z. Mathematical modeling of creep and shrinkage of concrete[M]. New York: John Wiley & Sons Ltd, 1988: 233−299.

[18] 颜东煌, 田仲初, 涂光亚, 等. 混凝土桥梁收缩徐变计算的有限元方法与应用[J]. 中国公路学报, 2004, 17(2): 55−58.YAN Donghuang, TIAN Zhongchu, TU Guangya, et al. Finite element method and application for the shrinkage and creep of concrete bridges[J]. China Journal of Highway and Transport, 2004, 17(2): 55−58.

[19] BUCKLER J D, SCRIBNER C F. Relaxation characteristics of prestressing strand[R]. Illinois: University of Illinois. Prestressed Concrete Institute, 1985: 30−34.

[20] ATIENZA J M, ELICES M. Role of residual stresses in stress relaxation of prestressed concrete wires[J]. Journal of Materials in Civil Engineering, 2007, 19(8): 703−708.

(编辑 陈灿华)

Incremental analysis considering coupling temperature and time-dependent effects of concrete bridge

LIN Ming1, 2, FU Hongyuan1, YAN Donghuang1

(1. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha 410114, China;2. Hunan Province Transport Planning, Survey and Design Institute Co., Ltd, Changsha 410008, China)

In order to understand the changes of the structural effect of concrete bridge during the construction and service period, which was influenced by those time-varying factors (such as elastic modulus, shrinkage and creep of concrete and relaxation of prestressed steel bar, etc) and the coupling of temperature effect. Based on the division of time series and the incremental virtual work equilibrium equation, the finite element solution equation was derived considering the coupling of temperature variation and material time-varying factors. Combined with the specific expression of time-varying function, the formula was modificated of the time-dependent elastic modulus of concrete under the action of temperature coupling. The expression of the load at the end of the beam with the increment of one dimensional beam element in time increment step was established. Combined with the actual engineering, the proposed calculation method was programmed; the calculation results of the coupling effect of temperature and dis-coupling effect of temperature and the measured value were contrasted. The results show that the long-term deflection calculated results of temperature coupling effect are in good agreement with the measured values, which shows that the incremental analysis and calculation method considering the coupling effect of temperature and time-varying characteristics can effectively improve the accuracy and reliability of the calculation and analysis of concrete bridges.

bridge engineering; shrinkage and creep; incremental load method; concrete bridge; stress relaxation

10.11817/j.issn.1672-7207.2017.09.032

U448.27

A

1672−7207(2017)09−2506−07

2017−02−17；

2017−04−22

国家自然科学基金资助项目(51178059) (Projects(51178059) supported by the National Natural Science Foundation of China)

林鸣，博士研究生，高级工程师，从事大跨度桥梁结构分析理论、施工监控与健康监测理论与应用研究；E-mail: nen-lin@126.com