基于离散缝洞网络模型的缝洞型油藏混合模型

严侠，黄朝琴，李阳，姚军，樊冬艳



基于离散缝洞网络模型的缝洞型油藏混合模型

严侠1，黄朝琴1，李阳2，姚军1，樊冬艳1

(1. 中国石油大学(华东) 石油工程学院，山东青岛，266580；2. 中国石化油田勘探开发事业部，北京，100728)

针对存在大尺度导流裂缝的复杂缝洞型油藏，为了克服目前常用数学模型不能准确高效对其进行流动模拟的缺陷，提出一种新的混合模型。首先根据缝洞的结构特征划分合适的正交网格，在每个网格单元内建立离散缝洞网络模型(DFVN)，基于超样本技术和体积平均方法求得网格单元的等效渗透率张量，对小尺度的缝洞结构进行等效处理；以形成的正交网格为基础建立嵌入式离散裂缝模型，对大尺度导流裂缝进行显示处理，并基于模拟有限差分方法建立能准确处理全张量形式渗透率的数值计算格式；最后通过单相稳定渗流数值算例验证本文方法的正确性和优越性。研究结果表明：对于缝洞结构易发生变化的油藏，只需根据变化后的缝洞结构进行局部的参数修正，避免了类似于离散缝洞网络模型的整体网格重构，有效提高了计算效率。

缝洞型油藏；离散缝洞网络模型；超样本技术；嵌入式离散裂缝模型；模拟有限差分

缝洞型碳酸盐岩油气藏属于非常规油气藏，其储量规模较大。在世界已探明储量中，碳酸盐岩油气藏储量约占50%，产量占60%以上。我国碳酸盐岩油气藏储量也十分可观，是今后增储的主要领域[1]。然而，由于这类油气藏构造及流动模式十分复杂，因此，如何准确模拟缝洞型油藏中的流体流动成为一项具有挑战性的研究工作。目前用于缝洞型油藏流动数值模拟的数学模型主要有等效连续介质模型[2−3]、多重介质模型[4−7]以及离散缝洞网络模型[8−9]。等效连续介质模型是以等效渗透率为基础，用连续介质方法描述渗流问题的数学模型。其突出优点是可以利用各向异性连续介质理论进行分析。该模型的关键问题是等效渗透率的求取以及全张量的数值模拟方法。目前，缝洞型介质等效渗透率的计算方法主要是基于流动模拟的方法，可以分为2类：一类是基于宏观达西定律的流量等效方法[10−12]，另一类是基于均化理论的尺度升级方法[13−14]。这些方法在处理小尺度缝洞时可以得到较准确的结果，但处理大尺度导流裂缝时往往会低估其强导流能力，致使得到的结果误差较大[15]。多重介质模型适用于油田规模数值模拟，在一定程度上反映了缝洞型油藏中的优先流现象，并考虑裂缝系统、基岩系统和溶洞系统间的流体交换，比较符合实际。但被裂隙分割的基岩和溶洞系统被假定具有相同的大小和形状，过于简化而不能充分表现缝洞型油藏的强各向异性、不连续性等特征。同时该模型窜流系数难以确定，并且不适用于含有若干不连通大尺度导流缝洞的油藏。离散缝洞网络模型将缝洞显式表征，基岩和裂缝系统视为渗流区域，溶洞系统视为自由流区域，是离散裂缝模型的有效延伸，属于宏观尺度的精细模型，能准确刻画出缝洞型油藏中的流动特征，但受目前计算机硬件和数值模拟技术的制约，只能处理小规模的缝洞型油藏。鉴于以上各模型对存在大尺度裂缝的缝洞型油藏难以进行高效准确的流动模拟，本文作者将离散介质模型与等效连续介质模型相结合：对于小尺度裂缝和溶洞，基于离散缝洞网络模型运用超样本技术和体积平均方法计算等效渗透率张量，对其进行等效处理；对于大尺度裂缝，采用嵌入式离散裂缝模 型[15−17]进行显示处理，在减小计算复杂度的同时保证了计算精度。

1 离散缝洞网络模型

岩和裂缝系统视为渗流区域，其运动方程符合Darcy定律，即：

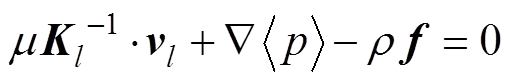
式中：为流体黏度，mPa∙s；为渗透率，μm2；为渗流速度，m/s；对于岩块，=m，对于裂缝，=f；为多孔介质中的平均压力，Pa；为流体密度，kg/m3；为单位质量力，m/s2。

溶洞的空间尺度较大，其流动模式为黏性流体的自由流动，为简单起见本文仅考虑牛顿流体的低雷诺数运动。为了避免引入复杂的耦合边界条件，降低自由流−渗流耦合问题的复杂性，本文采用Brinkman方程描述溶洞内的自由流：

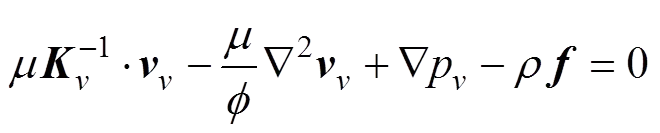
式中：为流体真实速度，m/s；为溶洞内渗透率(无充填时为无穷大)，μm2；为溶洞内孔隙度(无充填时为1)；p为流体压力，Pa。

考虑等温过程的单相稳态流动，上述运动方程的统一形式结合质量守恒方程得到离散缝洞网络模型的控制微分方程组：

式中：

；

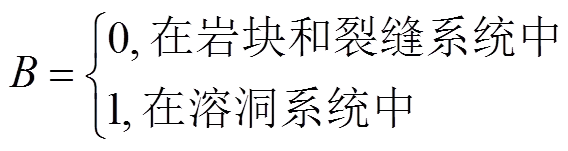
结合合适的边界条件可得到完整的离散缝洞网络单相稳态渗流数学模型。

2 混合模型原理

由于实际的缝洞型油藏中不仅存在小尺度的裂缝和溶洞，还存在贯穿大部分油藏区域的大尺度高导流裂缝，对于这类实际油藏，单独采用等效连续介质模型和多重介质模型往往得不到准确的计算结果，离散缝洞网络模型虽然可以准确刻画出缝洞型油藏中的流动特征，但其计算量较大，仅适用于小范围的油藏 模拟。

本文对油藏中的小尺度裂缝和溶洞(裂缝长度和溶洞大小与所划分的正交网格尺寸相差不大)通过超样本技术和体积平均法结合离散缝洞网络模型进行等效处理，得到整个油藏的等效渗透率场；对于大尺度的裂缝(裂缝长度远大于正交网格尺寸)，采用嵌入式离散裂缝模型将裂缝直接嵌入到前面通过等效计算得到的非均质各向异性油藏中。混合模型的整体计算过程如图1所示。

2.1 小尺度裂缝及溶洞等效处理

2.1.1 超样本技术

目前，基于流量等效计算等效渗透率的方法，都将各个网格单独考虑而忽略网格周围介质对它的影响，这样得到的等效渗透率往往不准确。对此，本文对网格进行超样本技术处理，首先获取每个网格的超样本单元；然后在超样本单元内建立离散缝洞网络模型并进行有限元数值求解，从而获取超样本单元内的压力和速度场；最后，基于体积平均法计算目标网格内的速度、压力梯度的体积平均值，求取目标网格的等效渗透率张量。

超样本处理是将目标原始网格及其周围网格组成一个大的超样本单元，如图2所示，以二维系统为例：当网格在角落时，超样本网格中包含4个网格；当网格在边界上时，超样本网格中有6个网格；当网格在内部时，超样本网格包含9个网格。

图1 混合模型计算过程示意图

(a) 含有1条裂缝的裂缝性介质网格示意图；(b) 网格在角落超样本处理图；(c) 网格在内部超样本处理图；(d) 网格在边界超样本处理图

2.1.2 等效渗透率计算

在超样本单元内结合封闭定压边界条件建立离散缝洞网络模型，采用有限单元法进行求解(具体的求解过程见参考文献[8])，根据求得的压力及速度场，运用体积平均法求取目标原始网格上的速度跟压力梯度的体积平均值[18]：

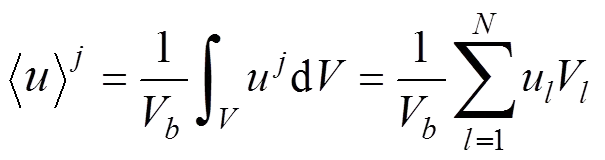
(5)

(6)

根据以上公式可以求得等效渗透率张量。由于定压封闭边界条件下得到的等效渗透率并不一定是对称的，这时可以取取。

2.2 大尺度裂缝显示处理

通过等效处理将只包含小尺度缝洞的油藏转化为非均质各向异性油藏。由于之前计算油藏等效渗透率场时已划分了正交网格，采用嵌入式离散裂缝模型将大尺度裂缝直接嵌入到正交网格系统中，以裂缝与正交网格边界相交的交点对裂缝进行网格划分。此时数学模型为：

等效基质系统：

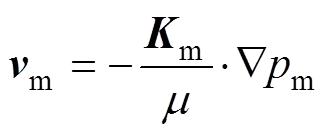
(8)

大尺度裂缝系统：

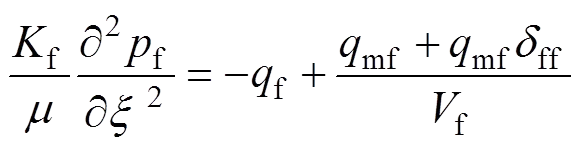
式中：m为基质中渗流速度；m为基质的等效渗透率张量；f为大尺度裂缝渗透率；m和f分别为基质和裂缝的流体压力；f和m分别为裂缝单元和基质单元的体积；m和f分别为基质和裂缝的源汇项；为沿裂缝方向的局部坐标系；mf为基岩与裂缝之间的窜流量；ff为相交裂缝单元之间的窜流量；

；

借鉴常规油藏数值模拟方法中生产井和网格单元间流量交换的计算格式，可以将基岩与裂缝之间的窜流量表达式定义为

(10)

与网格尺度相比，裂缝开度很小，且裂缝渗透率远大于基岩渗透率，因此可以认为裂缝两侧的压力连续，根据达西定律，基岩与裂缝间的窜流量为[15]

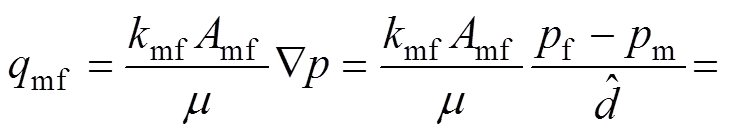
(11)

本文采用Karimi-Fard[19]计算相交裂缝段间传递系数的方法计算裂缝与裂缝间窜流量[16]：

3 混合模型求解

由于求得的各基质网格等效渗透率为全张量形式，因此，本文采用模拟有限差分方法对基质部分的方程进行离散。作为一种新型数值计算方法，模拟有限差分具有良好的局部守恒性和对复杂网格的适用性，并且能有效地处理全张量渗透率问题[20]。而大尺度裂缝渗透率考虑为标量，因此，采用有限差分隐式离散。

3.1 大尺度裂缝显示处理

基质部分被正交网格所剖分，如图3所示，取任意单元Ω进行分析，其中Ω为其相邻单元，交界面，为交界面A的面积加权法向量，为单位外法线向量。在单元中心点和边界面中心点上分别定义单元平均压力和边界面平局压力。

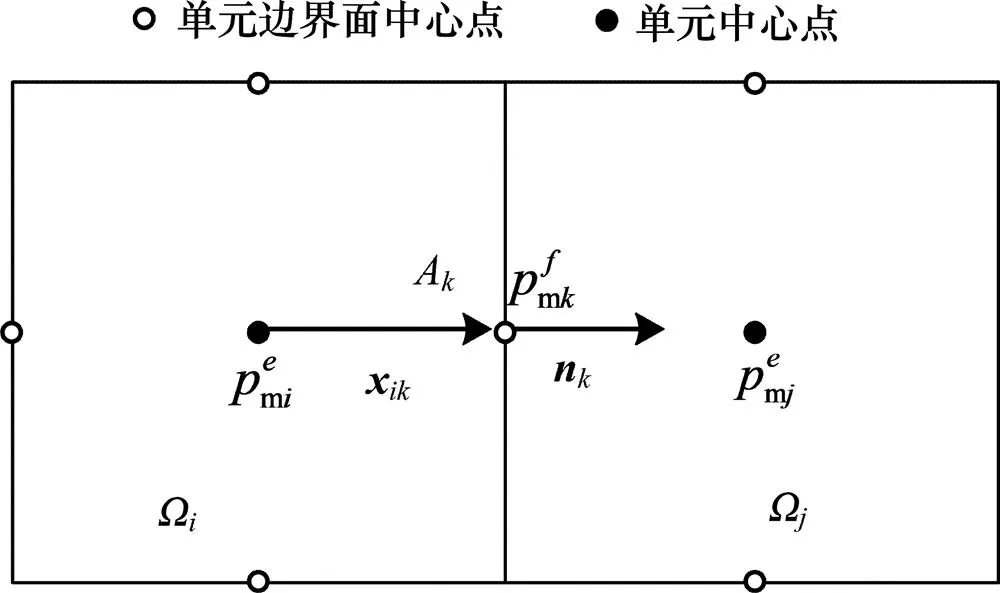
图3 模拟有限差分网格单元分析示意图

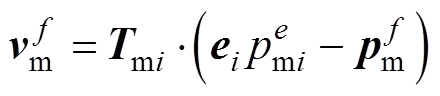
其中：mi为基质网格的传导矩阵，，为单元Ω的边界面数，，因此，模拟有限差分方法的关键问题是获取矩阵mi。在此，假设压力在基质网格内呈线性变化，即，显然，由方程(7)可得：

(14)

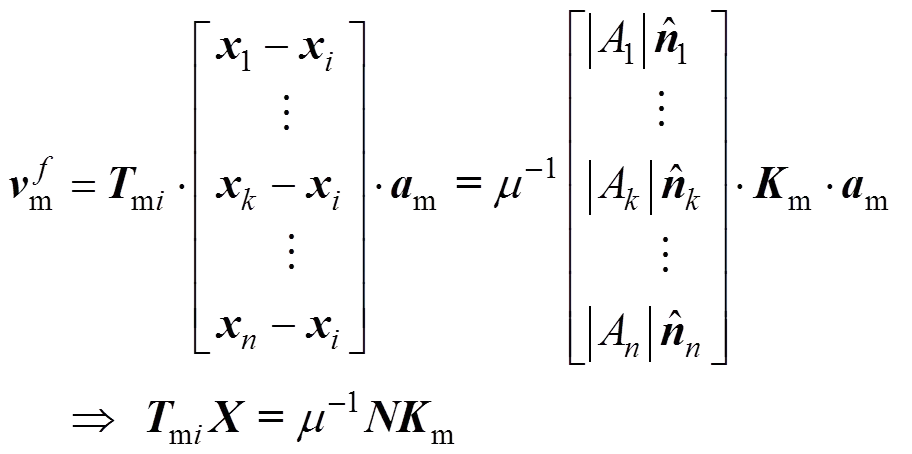
(16)

式中：

(18)

对于方程(8)，直接在基质网格单元上积分并运用散度定理：

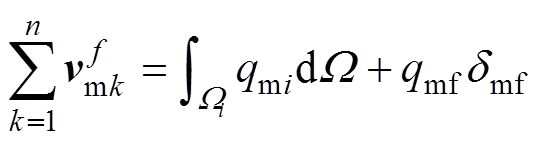
考虑单元边界面上的速度连续条件，结合方程(13)和(19)，得到基质部分模拟有限差分的数值计算格式：

(20)

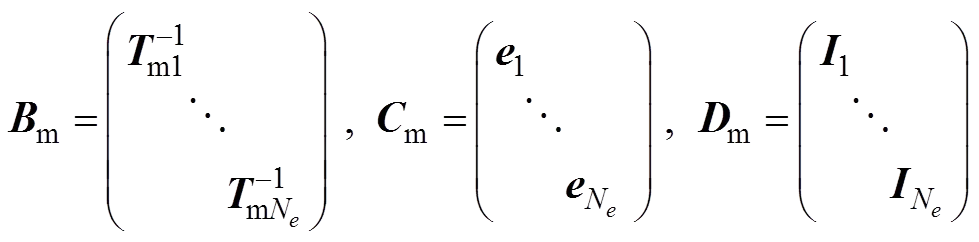
其中：N为网格单元总数；i=。

3.2 裂缝部分有限差分隐式离散

对于一维裂缝系统采用隐式差分，方程左右两端同乘网格单元体积，则式(9)的差分方程为

3.3 整体计算格式

以存在2条交叉裂缝为例，将基质部分和裂缝部分的数值计算格式组装到一起，得到基于模拟有限差分的嵌入式离散裂缝模型计算方式：

(23)

其中：mfi=[mfi]，表示第条裂缝与基岩窜流系数矩阵；ff=[ff]，表示裂缝之间的窜流系数矩阵；fi和fi分别表示第条裂缝的有限差分传导系数矩阵和裂缝单元压力列阵。多条裂缝的计算格式与上类似。

4 算例分析

通过分析单相稳定渗流模拟算例，并离散介质模型结果对比，说明本文方法的正确性和优越性。离散介质模型(离散裂缝模型和离散缝洞网络模型)作为一种宏观精细模型，国内外学者通过物理实验[16, 22−23]以及数值实验[8−9, 19]等方法对其准确性进行了验证，结果表明离散介质模型能准确刻画缝洞型油藏中的流动特征。因此，本文中将离散介质模型作为对比验证的 标准。

4.1 二维复杂裂缝性油藏

100 m×100 m裂缝性油藏几何模型如图4(a)所示，其中存在2条长度分别为82.5 m和60.8 m的大尺度导流裂缝，裂缝开度和渗透率如表1所示。图4(b)和图4(c)所示分别为10×10正交网格和20×20正交网格的划分结果。模型其他参数如表1所示。

表1 裂缝性油藏模型基本参数

不考虑大尺度裂缝时的裂缝性油藏如图5(a)所示，通过划分粗网格，建立离散裂缝模型并结合超样本技术和体积平均法，得到该裂缝性油藏的等效渗透率场，见图5(b)和图5(c)。

分别运用离散裂缝模型(图6(a))和本文提出的混合模型结合封闭定压边界条件(上、下边界封闭，左、右边界定压，压力值分别为1 MPa和2 MPa)对该裂缝性油藏进行单相稳定渗流模拟，其中混合模型分别10×10网格系统(图6(b))和20×20网格系统(图6(c))求解。图7所示为=50 m直线上各方法求得的压力分布曲线。通过式(24)可进一步计算各方法相应的误差范数0。

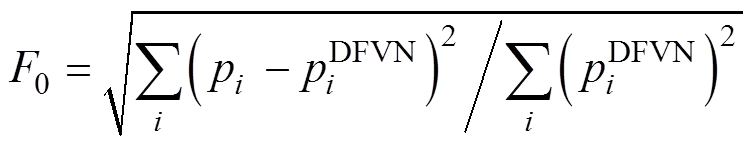
从图7可以看出：2种方法的模型结果都能够反映出裂缝性油藏基本流动特征：裂缝内压力传播快，大裂缝及周围相连的小裂缝构成明显的等势体，同时其他小裂缝也在一定程度上增加了油藏的非均质性。采用混合模型时，10×10的网格系统得到的压力场分布与离散裂缝模型有一定偏差，误差范数为2.2%，而采用20×20网格系统时混合模型的压力场分布与离散裂缝模型的基本一致，误差范数为0.85%。因此，本文提出的混合模型可以有效地模拟复杂裂缝性油藏中单相渗流压力场分布，同时，可以看出网格划分对于模型精度有一定影响。

(a) 裂缝性油藏几何模型；(b) 10×10的正交网格系统；(c) 20×20的正交网格系统

图4 裂缝性油藏几何模型及网格划分结果

Fig. 4 Geometrical model and grids of fractured reservoir

(a) 裂缝性油藏几何模型；(b) 10×10的正交网格系统；(c) 20×20的正交网格系统

(a) 离散裂缝模型；(b) 混合模型(10×10)；(c) 混合模型(20×20)

1—离散裂缝模型(参考解)；2—混合模型(20×20)；3—混合模型(10×10)。

4.2 二维复杂缝洞型油藏

100 m×100 m缝洞型油藏几何模型如图8(a)所示，其中存在3条长度分别为70.7，99.0和70.7 m的大尺度导流裂缝，裂缝开度和渗透率如表1所示。模型其他参数如表1所示，其中溶洞部分视为无充填的自由流。图8(b)所示为20×20正交网格划分结果。图8(c)所示为求得的不考虑大尺度裂缝时的等效渗透率场图。

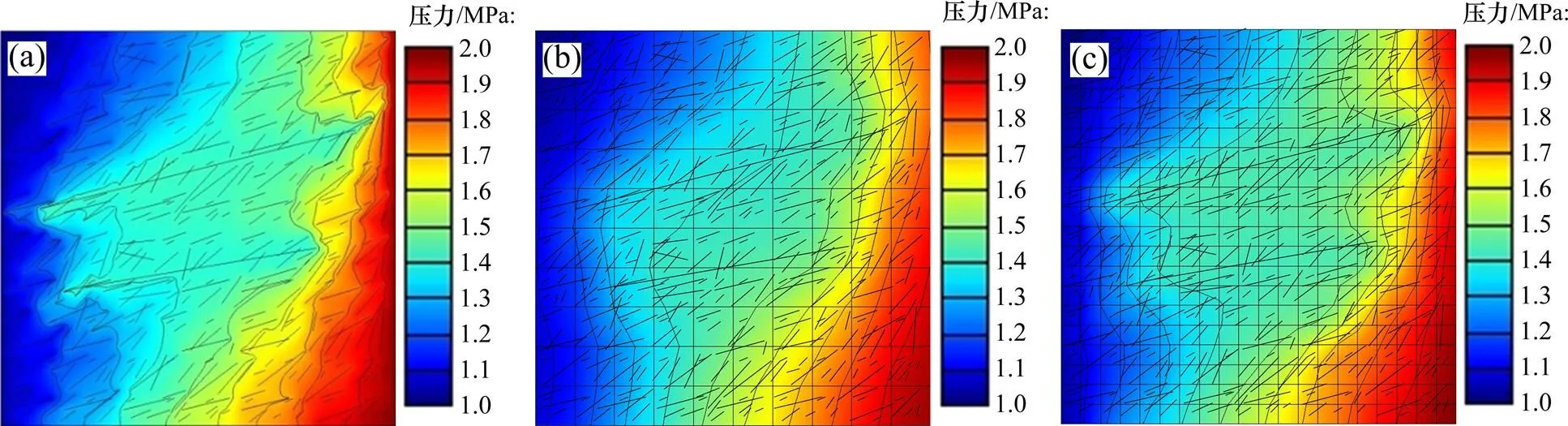
分别运用离散缝洞网络模型(图9(a))和本文提出的混合模型(图9(b))结合封闭定压边界条件(上、下边界封闭，左、右边界定压，压力分别为1 MPa和2 MPa)对缝洞型油藏进行单相稳定渗流模拟。图10所示为=47.5 m和=52.5 m直线上2种方法求得的压力分布曲线。

从图10可以看出：模拟结果能够反映出缝洞型油藏基本流动特征。裂缝和溶洞内压力传播快，大裂缝及周围相连的小缝洞构成明显的等势体，同时其他小缝洞也在一定程度上增加了油藏的非均质性。采用混合模型20×20的网格系统得到的压力场分布与离散缝洞网络模型的结果基本一致，其误差范数分别为1.2%和1.1%。因此，本文提出的混合模型同样适用于二维复杂缝洞型油藏单相流模拟。并且本文模型对于缝洞参数易发生变化的油藏，当局部小尺度缝洞结构发生变化，只需要更新这部分的等效参数，而当大尺度裂缝结构发生变化时，只需要重新划分该大尺度裂缝网格并更新裂缝与基质之间的窜流信息，从而避免了离散缝洞网络模型那样的整体网格重新划分，可以有效提高计算效率，图9(c)所示为当大尺度裂缝结构发生变化后的压力场计算结果。

(a) 缝洞型油藏几何模型；(b) 20×20的正交网格系统；(c) 等效渗透率场图

(a) DFVN；(b) 混合模型；(c) 大尺度裂缝结构发生改变

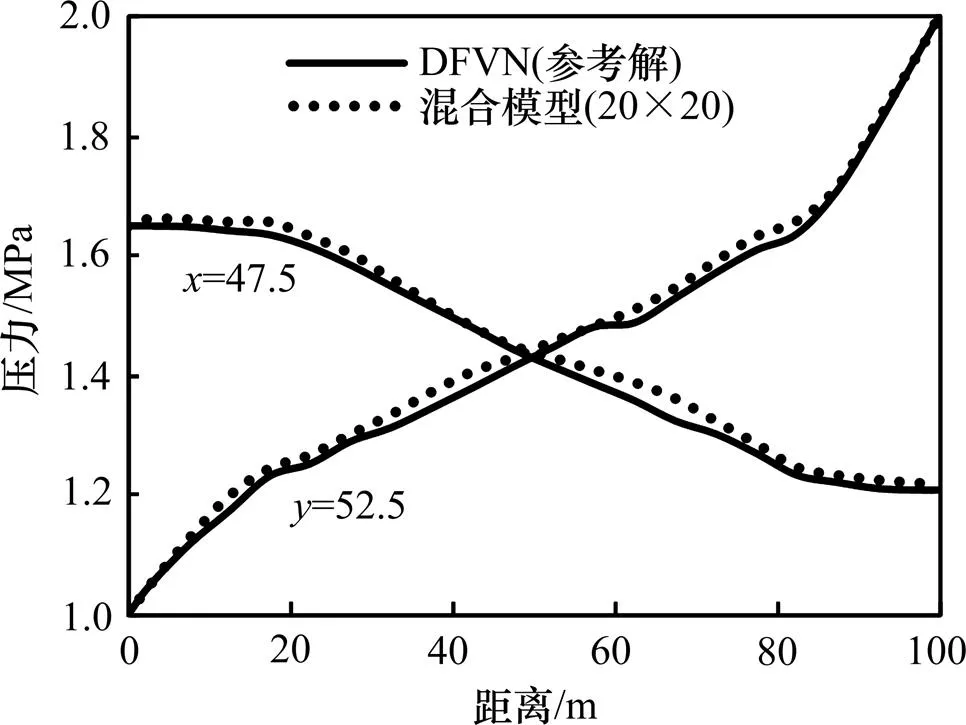
图10 不同位置压力对比曲线

4.3 三维复杂缝洞型油藏

根据某一实际缝洞型油藏的裂缝、溶洞信息统计资料，生成相应的三维复杂缝洞型油藏几何模型，其长×宽×高为200 m×100 m×20 m，如图11所示。其中裂缝在垂直方向上都贯穿地层，溶洞简化成半径为4 m的规则球体，溶洞内不考虑充填，其流动视为自由流。模型参数如表2所示。

表2 三维缝洞型油藏模型基本参数

分别运用离散缝洞模型(图12(a))和本文方法(图12(b))，结合封闭定压边界条件(左边界1和右边界2定压，压力分别为1 MPa和2 MPa，其余边界均为封闭边界)对该复杂缝洞型油藏进行单相稳定渗流模拟。图13所示为地层上表面=50 m直线上2种方法求得的压力曲线，可以看出两者结果吻合很好。因此，本文方法对于三维复杂缝洞型油藏同样适用。

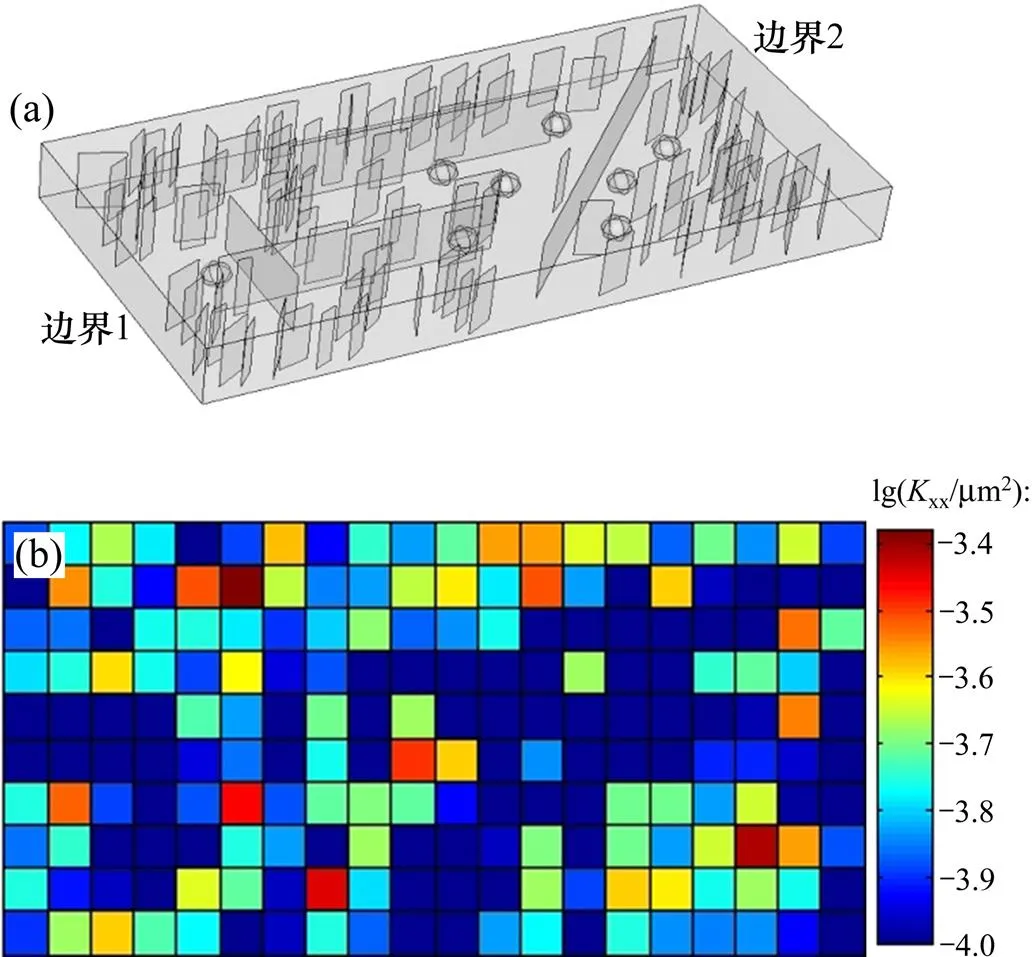
(a) 缝洞型油藏几何模型；(b) 等效渗透率场

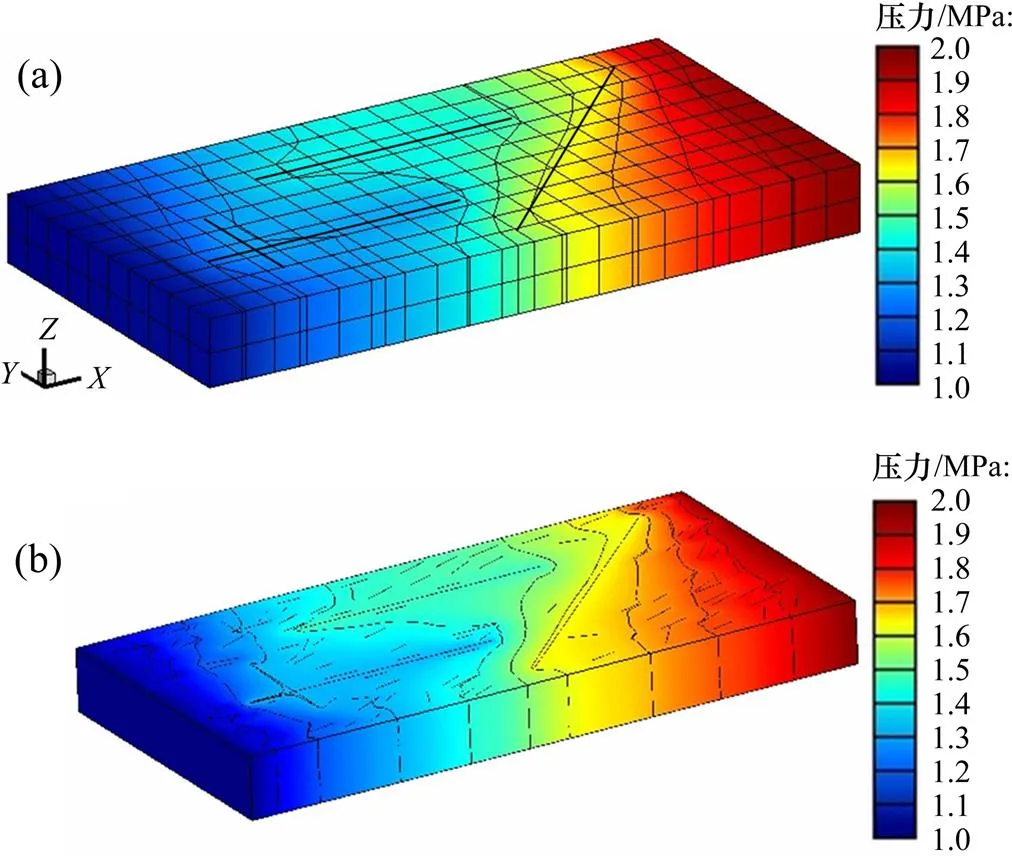
(a) DFVN；(b) 混合模型

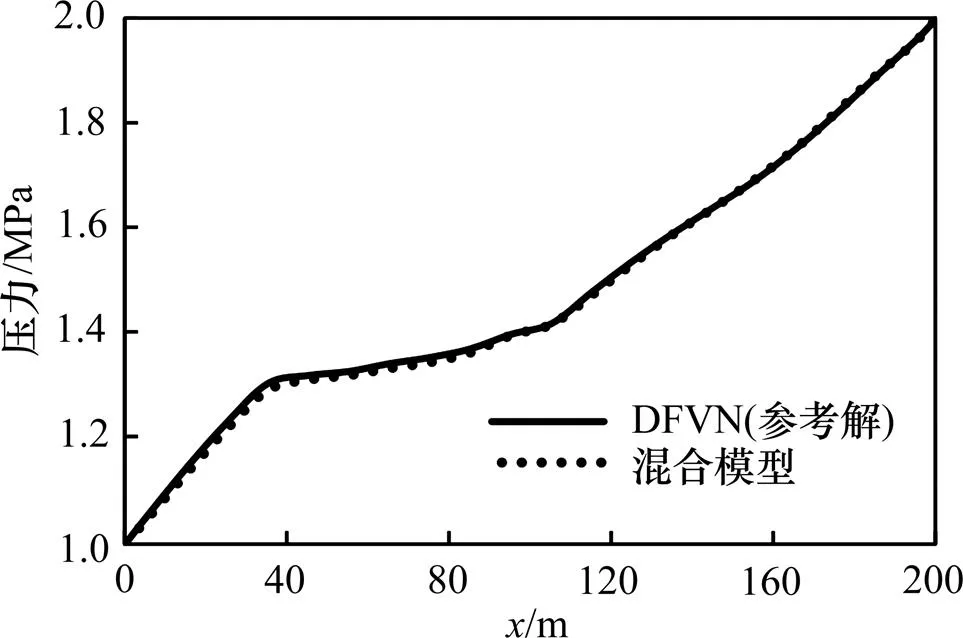
图13 上表面y=50 m线上的压力分布比较

5 结论

1) 将离散介质模型与等效连续介质模型相结合：对于小尺度裂缝和溶洞，基于离散缝洞网络模型采用超样本技术和体积平均方法对其进行等效处理；对于大尺度裂缝，采用嵌入式离散裂缝模型进行显示处理；并基于模拟有限差分方法构造了可以准确处理全张量形式等效渗透率的数值计算格式。

2) 本文方法对于复杂缝洞型油藏单相稳定渗流模拟有较高的准确性和灵活性。

[1] 李阳. 塔河油田碳酸盐岩缝洞型油藏开发理论及方法[J]. 石油学报, 2013, 34(1): 115−121. LI Yang. The theory and method for development of carbonate fractured-cavity reservoirs in Tahe oilfield[J]. Acta Petrolei Sinica, 2013, 34(1): 115−121.

[2] 李亚军. 缝洞型介质等效连续模型油水两相流动模拟理论研究[D]. 青岛: 中国石油大学石油工程学院, 2011: 17−64. LI Yajun. Theoretical study of the equivalent continuum model for simulating oil-water two-phase flow in fractured-vuggy porous media[D]. Qingdao: China University of Petroleum. School of Petroleum Engineering, 2011: 17−64.

[3] HUANG Zhaoqin, YAO Jun, WANG Yueying. An efficient numerical model for immiscible two-phase flow in fractured Karst reservoirs[J]. Communications in Computational Physics, 2013, 13(2): 540−558.

[4] 吴玉树, 葛家理. 三重介质裂−隙油藏中的渗流问题[J]. 力学学报, 1983, 19(1): 81−85. WU Yushu, GE Jiali. The transient flow in naturally fractured reservoirs with three-porosity systems[J]. Chinese Journal of Theoretical and Applied Mechanics, 1983, 19(1): 81−85.

[5] ABDASSAH D, ERSHAGHI I. Triple-porosity systems for representing naturally fractured reservoirs[J]. SPE Formation Evaluation, 1986, 1(2): 113−127.

[6] 杨坚, 姚军, 王子胜. 三重介质复合油藏压力动态特征研究[J]. 水动力学研究与进展(A辑), 2005, 20(4): 418−425. YANG Jian, YAO Jun, WANG Zisheng. Study of pressure-transient characteristic for triple-medium composite reservoirs[J]. Journal of Hydrodynamics (Series A), 2005, 20(4): 418−425.

[7] WU Yushu, QIN Guan, EWING R, et al. A multiple-continuum approach for modeling multiphase flow in naturally fractured vuggy petroleum reservoirs[C]// SPE International oil & Gas Conference and Exhibition. Beijing: SPE, 2006: 1−12.

[8] 姚军, 黄朝琴, 王子胜, 等. 缝洞型油藏的离散缝洞网络流动数学模型[J]. 石油学报, 2010, 31 (5): 15−20. YAO Jun, HUANG Zhaoqin, WANG Zisheng, et al. Mathematical model of fluid flow in fractured vuggy reservoirs based on discrete fracture-vug network[J]. Acta Petrolei Sinica, 2010, 31(5): 815−819.

[9] YAO Jun, HUANG Zhaoqin, LI Yajun, et al. Discrete fracture-vug network model for modeling fluid flow in fractured vuggy porous media[C]// The CPS/SPE International Oil & Gas Conference and Exhibition. Beijing, China: SPE 2010: 1−14.

[10] 李亚军, 姚军, 黄朝琴, 等. 基于Darcy-Stokes 耦合模型的缝洞型介质等效渗透率分析[J]. 中国石油大学学报(自然科学版), 2011, 35(2): 91−95. LI Yajun, YAO Jun, HUANG Zhaoqin, et al. Estimating equivalent permeability of fractured-vuggy media based on coupled Darcy-Stokes model[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(2): 91−95.

[11] 李亚军, 姚军, 黄朝琴, 等. 裂缝性油藏等效渗透率张量计算及表征单元体积研究[J]. 水动力学研究与进展(A辑), 2010, 25(1): 1−7. LI Yajun, YAO Jun, HUANG Zhaoqin, et al. Calculation of equivalent permeability tensor and study on representative element volume for modeling fractured reservoirs[J]. Journal of Hydrodynamics (Series A), 2010, 25(1): 1−7.

[12] 张世明, 严侠, 孙红霞, 等. 基于离散裂缝模型的裂缝性介质等效渗透率求解新方法[J]. 科学技术与工程, 2014, 14(16): 36−40. ZHANG Shiming, YAN Xia, SUN Hongxia, et al. An efficient calculation of equivalent permeability of fractured porous media based on discrete fracture model[J]. Science Technology and Engineering, 2014, 14(16): 36−40.

[13] HUANG Zhaoqin, YAO Jun, LI Yajun, et al. Permeability analysis of fractured vuggy porous media based on homogenization theory[J]. Science China Technological Sciences, 2010, 53(3): 839−847.

[14] HUANG Zhaoqin, YAO Jun, LI Yajun, et al. Numerical calculation of equivalent permeability tensor for fractured vuggy porous media based on homogenization theory[J]. Communications in Computational Physics, 2011, 9(1): 180−204.

[15] LI L, LEE S H. Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media[J]. SPE Reservoir Evaluation & Engineering, 2008, 11(04): 750−758.

[16] 严侠, 黄朝琴, 姚军, 等. 基于模拟有限差分的嵌入式离散裂缝数学模型[J]. 中国科学:技术科学, 2014, 44(12): 1333−1342. YAN Xia, HUANG Zhaoqin, YAO Jun, et al. The embeded discrete fracture model based on mimetic finite difference method[J]. Science China: Technological Sciences, 2014, 44(12): 1333−1342.

[17] ZHOU Fangqi, SHI Anfeng, WANG Xiaohong. An efficient finite difference model for multiphase flow in fractured reservoirs[J]. Petroleum Exploration and Development, 2014, 41(2): 262−266.

[18] DURLOFSKY L J. Upscaling and gridding of fine scale geological models for flow simulation[C]// 8th International Forum on Reservoir Simulation Iles Borromees, Stresa, Italy. 2005: 20−24.

[19] KARIMI F M, DURLOFSKY L J, AZIZ K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators[J]. SPE Journal, 2004, 9(2): 227−236.

[20] LIPNIKOV K, MANZINI G, SHASHKOV M. Mimetic finite difference method[J]. Journal of Computational Physics, 2014, 257: 1163−1227.

[21] BREZZI F, LIPNIKOV K, SIMONCINI V. A family of mimetic finite difference methods on polygonal and polyhedral meshes[J]. Mathematical Models and Methods in Applied Sciences, 2005, 15(10): 1533−1551.

[22] 黄朝琴, 高博, 王月英, 等. 基于模拟有限差分法的离散裂缝模型两相流动模拟[J]. 中国石油大学学报(自然科学版), 2014, 38(6): 97−105. HUANG Zhaoqin, GAO Bo, WANG Yueying, et al. Two-phase flow simulation of discrete fracture model using a novel mimetic finite difference method[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014, 38(6): 97−105.

[23] YAN Xia, HUANG Zhaoqin, YAO Jun, et al. An efficient embedded discrete fracture model based on mimetic finite difference method[J]. Journal of Petroleum Science and Engineering, 2016, 145: 11−21.

(编辑 赵俊)

An efficient hybrid model for fractured-vuggy reservoir based on discrete fracture-vug network model

YAN Xia1, HUANG Zhaoqin1, LI Yang2, YAO Jun1, FAN Dongyan1

(1. School of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China;2. Department of Oilfield Exploration & Development, SINOPEC, Beijing 100728, China)

The existing numerical simulation methods are inaccurate or inefficient when modeling the flow and transport processes in fractured-vuggy reservoir with long fractures. A numerically efficient hybrid model was proposed to solve this problem, in which small fractures and vugs were modeled by equivalent permeability tensor, and long fractures were modeled by embedded discrete fracture model. Firstly, the orthogonal grid system was made according to the structure characteristics of fractures and vugs. Then, the discrete fracture-vug model (DFVN) was implemented in each orthogonal grid to calculate equivalent permeability tensor based on volume average method and oversampling technology, and the long fractures were embedded in equivalent media system. After that, an efficient numerical simulator was devised to solve the coupled system of long fracture and equivalent media based on mimetic finite difference method. At last, several single-phase steady numerical examples were shown to verify the validity and accuracy of the hybrid model. The results show that the proposed model is suitable for the fractured-vuggy reservoirs with dynamically changing fractures and vugs, because they can be simulated with an element effectively adapting itself to changes. Therefore the challenges associated with the remeshing for whole reservoirs, which has to be done in the DFVN, are bypassed entirely, and the computational costs can be reduced greatly.

fractured-vuggy reservoir; discrete fracture-vug network model; oversampling technology; embedded discrete fracture model; mimetic finite difference

10.11817/j.issn.1672-7207.2017.09.028

TE319；O241.82

A

1672−7207(2017)09−2474−10

2016−09−01；

2016−12−22

国家自然科学基金资助项目(51404292，51234007，51504277)；山东省自然科学基金资助项目(ZR2014EEQ010)；中央高校基本科研业务费专项资金资助项目(15CX05037A，14CX06091A)；中国石油大学(华东)研究生创新工程资助项目(YCXJ2016015) (Projects(51404292, 51234007, 51504277) supported by the National Natural Science Foundation of China; Project(ZR2014EEQ010) supported by Shandong Provincial Natural Science Foundation, China; Projects(15CX05037A, 14CX06091A) supported by the Fundamental Research Funds for the Central Universities; Project(YCXJ2016015) supported by the Innovative Project of China University of Petroleum)

黄朝琴, 博士，从事复杂介质渗流理论及油藏数值模拟；E-mail: huangzhqin@upc.edu.cn