新型斜线齿面齿轮齿宽的几何设计

苏进展，张昆仑，方宗德



新型斜线齿面齿轮齿宽的几何设计

苏进展1, 2，张昆仑1，方宗德3

(1. 长安大学道路施工技术与装备教育部重点实验室，陕西西安，710064；2. 重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆，400054；3. 西北工业大学机电学院，陕西西安，710072)

为了满足航空传动的紧凑空间设计要求，研究一种新型点接触斜线齿面齿轮及其齿宽设计。根据渐开线插齿刀方程，模拟插齿刀与工件的运动关系，推导斜线齿面齿轮的齿面方程；建立内端根切、外端变尖、限定工作齿高和避免二次切削等限制条件，计算面齿轮的有效齿宽。分析倾斜角、交点位置对内径、外径及齿宽的影响。研究结果表明：减小刀顶圆角半径可避免齿根发生二次切削；增大倾斜角和交点位置的增量，面齿轮的内径和外径都增大，而有效齿宽却减小。

斜线齿面齿轮；齿根根切；齿顶变尖；二次切削；齿宽设计

面齿轮传动是圆柱齿轮与平面齿轮相啮合的角度传动，可用于两轴线正交、非正交或偏置等情况。近年来，由于面齿轮在分流传动中所表现出的潜在优势，使得其成为航空动力传输领域的研究热点，出现了诸如直齿、斜齿及其偏置形式的面齿轮传动，更有新型弧线齿面齿轮的传动类型。鉴于直齿面齿轮重合度低、斜齿面齿轮存在轴向力，提出一种新型点接触斜线齿面齿轮，其齿线近似为斜线并与半径方向形成倾斜角，仅能与直齿轮相啮合，不能与斜齿轮啮合。齿面是由渐开线插齿刀斜交错插削而成，而点接触则是通过插齿刀齿数多于直齿轮1~3个齿来实现的[1]。由于斜线齿面齿轮的配对齿轮是直齿轮，不产生轴向力，具有简化支撑结构和易于实现浮动均载等优点，且两轴线为倾斜交错安装，非常适应于航空的紧凑空间设计的多样化需求。齿宽设计是面齿轮传动要解决的关键问题，LITVIN等[1−4]从几何学角度推导直面齿轮根切和齿顶变尖的条件；在此基础上，ZHANG等[5]研究了偏置直齿面齿轮的齿宽设计。在国内，朱如鹏等[6]根据啮合角变化，得出了齿宽设计的基本公式。李政民 卿[7]采用包络理论进行齿宽设计。沈云波等[8−11]推导斜齿面齿轮和偏置斜齿面齿轮的齿宽设计。李永祥等[12]讨论了变位插齿刀对齿宽及接触应力的影响。蔡香伟等[13−14]根据弧线齿面齿轮的展成原理，研究了内径和外径的计算方法。文献[15−18]研究了面齿轮齿宽对轮齿强度的影响规律。面齿轮的齿宽计算方法已较为成熟且为试验所验证，但上述文献鲜有讨论插齿刀齿顶圆角半径对内径的影响及给定内端工作齿高的齿宽设计。本文作者阐述了斜线齿轮面齿轮的插齿原理，推导面齿轮的齿面方程；利用插齿刀的界限线，求出内端齿根根切点的位置；通过外端齿顶齿厚等于零的条件，获得变尖的条件；再结合避免齿根二次切削发生的条件，确定刀顶圆角半径，最终获得面齿轮的齿宽，并分析倾斜角和交点位置对齿宽的影响规律，为该类面齿轮加工及应用奠定理论基础。

1 插齿原理及模型

1.1 插齿原理

斜线齿面齿轮的插齿加工是模拟渐开线直齿圆柱齿轮与斜线齿面齿轮的斜交啮合传动，两者运动类似于直齿面齿轮的插削过程；不同之处在于插齿刀轴线与节锥线的位置关系，前者是倾斜交错，而后者是平行关系。图1(a)所示，轴线c为平行于面齿轮的节锥线且距离等于插齿刀节圆半径的直线，轴线c交面齿轮轴线2于点2，插齿刀轴线s和轴线c的交点为s，交角为倾斜角c，点为节点，0为节点与2的距离，D为交点s相对节点的增量距离；图1(b)中，虚线为插削直齿面齿轮的位置，实线为插削斜线齿面齿轮的位置；插齿刀沿轴线s以速度s进行切削，是插齿机的主运动；插齿刀绕轴线s以角速度s旋转，被加工面齿轮绕轴线2以角速度2旋转，两者形成展成运动且满足s/2=2/s，2为面齿轮齿数，s为插齿刀齿数。实际加工时，将安装工件的夹具及相应的传动链绕s旋转c后，即可实现斜线齿面齿轮的插齿加工。完成一个轮齿的插削后，通过分度机构将轮坯旋转2p/2角度，继续插削下一个轮齿，直至插出所有轮齿。

(a) 插齿原理；(b) 郫齿运动关系

1.2 插齿刀方程

图2所示为渐开线插齿刀的截面示意图，包括展成面齿轮工作齿面的渐开线齿廓和加工过渡曲面的刀顶圆弧，坐标系s(s,s,s)为插齿刀坐标系，平面s=0是插齿刀齿槽的对称面。矢量由式(1)给出，

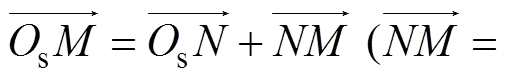
渐开线齿廓的位置矢量表示为[1]

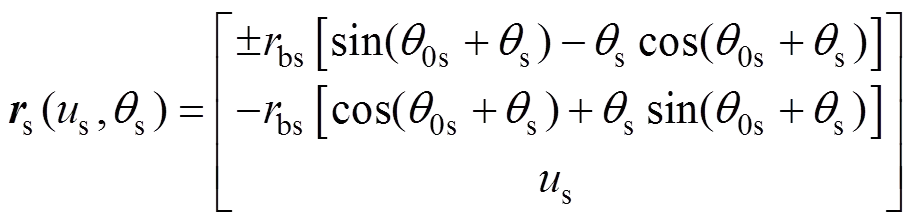
式中：bs=0.5nscos0为渐开线插齿刀的基圆半径，n为法向模数，0为插齿刀压力角；s为刀具齿面的轴线参数，s为刀具渐开线的角度参数，即渐开线的展角。式(2)中的正负号分别对应于刀具齿槽两侧的渐开线方程；0s=0.5p/s−inv0为插齿刀渐开线起点的角度，渐开线函数inv0=tan0−0。

渐开线齿廓的单位法线矢量为

在坐标系s中，刀顶圆弧的位矢表示为

(4)

式中：f为刀顶圆弧参数；c为刀顶圆角半径；f为插齿刀轴向参数；f和f为圆弧中心f的坐标，由式(5)确定：

式(5)的第1个等式表示刀顶圆弧和渐开线齿廓相切交点的位矢相等，第2个等式为圆弧与齿顶圆相切于点，as为插齿刀齿顶圆半径。求解式(5)计算出点的圆弧参数和展角参数，代入求出圆弧中心的坐标f，f。

2 面齿轮齿面方程

2.1 插齿加工坐标系

图3所示为斜线齿面齿轮加工过程的坐标系，其中动坐标系s和2分别与插齿刀、面齿轮固联；坐标系a和d分别为插齿刀、面齿轮的参考坐标，用于确定插齿刀转角s和面齿轮转角1，辅助坐标系b确定了插齿刀轴线s与面齿轮节锥线b的倾斜角c，辅助坐标系c用于确定与b的相对位置0，m为轴线c与面齿轮轴线2的交角。

图3 插齿加工坐标系

2.2 齿面展成

面齿轮齿面S2是由插齿刀的刀具面S包络展成，经过齐次坐标变换和啮合方程[1]，齿面的位置矢量表示为

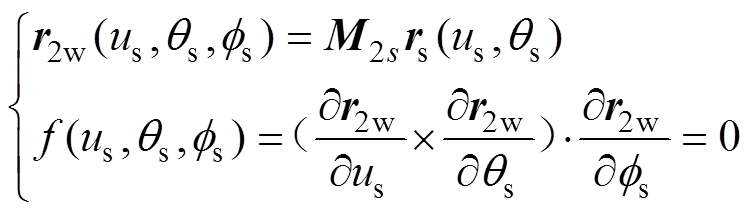
式中：2s=2ddccbbaas为刀具坐标系s到面齿轮坐标系2的变换矩阵；为插齿刀与面齿轮的啮合方程；和分别为工作齿面位矢对坐标参数和的偏导数；矢量表示工作齿面的法矢；为工作齿面位置矢量对插齿刀转角求偏导，表示加工工作齿面时插齿刀和面齿轮的相对速度。同理，过渡曲面的表达式为

(7)

3 齿宽限制条件

3.1 齿根根切

齿根根切是一种加工缺陷，易产生应力集中，降低轮齿的弯曲强度，造成齿轮过早失效，应该在几何参数设计阶段给予消除。避免根切可以通过限定刀具齿面Ss来实现。插齿刀齿面Ss的界限线用下列方程确定[19]

根切界限线上的点是根切极限点，即最先发生根切的位置。将代入式(8)中，求解出参数和；再将代入到式(6)中求出面齿轮发生根切起始点的坐标。则内端齿根不发生根切的内径为

由于斜线齿面齿轮齿面结构的不对称性，轮齿两侧不发生根切的内径需分别计算，记左、右侧根切起始点的坐标分别为和，将其代入式(9)，则两侧不发生根切的内径分别为和；另外，面齿轮内端齿根高不能太大，否则在有安装误差条件下，容易发生小轮齿顶和大轮齿根干涉的现象。设计时可预先给定内端工作齿高a2，通过式(10)求解插齿刀转角参数，获得齿面两侧对应点的坐标和，最后利用式(9)计算出给定工作齿高的两侧内径和。

面齿轮的内径1应取最大值，即。

3.2 齿根二次切削

为了提高刀具寿命和增加齿根强度，插齿刀都需刃磨出刀顶圆角。由于斜线齿面齿轮两侧齿面的不对称性，加工过渡曲面时容易产生齿根二次切削现象，即插削第二个轮齿左侧过渡曲面时会将第一个轮齿右侧过渡曲面的部分去除，是一种加工缺陷。由于面齿轮的过渡曲面区域是从外端往内端增加的，因此内端过渡曲面发生二次切削的可能性最大，应由刀顶圆弧的极限点展成。假设刀顶圆角半径c和内径1已知，极限点的圆弧参数，代入式(7)求得过渡曲面位置矢量；同时，内端过渡曲面的齿根点满足

(11)

两组患者入院后均接受基础的检查和治疗，两组患者均给予抗凝治疗，治疗方案上没有倾向性，差别仅在护理上。对照组患者给予生活护理、病情观察、饮食干预、健康指导等常规护理。

3.3 齿顶变尖

外端齿顶变尖是指轮齿的两侧齿面与齿顶圆锥面相交，使得齿顶厚等于0 mm；尖顶的出现削弱了在该区域轮齿的接触强度，应当避免齿顶变尖的发生。尖点位置通过求解式(13)获得。

(14)

最后，斜线齿面齿轮的有效齿宽=2-1。

4 算例

据上述设计方法，编写斜线齿面齿轮齿宽设计的计算程序。表1所示为斜线齿面齿轮的基本参数，图4所示为斜线齿面齿轮副的三维实体模型，图5所示为该面齿轮的齿宽设计流程。一般情况下，刀顶圆角半径c越大，齿根弯曲强度越好，但它会影响内径1和齿根二次切削，所以需迭代计算。初选文献[20]推荐值c=0.635 mm，内端工作齿高a2=5.357 8 mm时，内径1=170.782 1 mm，外径2=195.914 3 mm，旋转角lr=3.454 9°＞3.364 5°(=2p/2)，发生齿根二次切削；经过若干次迭代后，取c=0.455 0 mm时，内径1=173.683 0 mm，外径2=195.914 3 mm时，旋转角lr=3.364 5°，两侧过渡曲面平滑过渡，消除了齿根二次切削现象，但内径1略有增大，齿根二次切削比较见图6。

图7所示为斜线齿面齿轮一侧的齿面接触印痕。从图7可以看出：该齿轮副为点接触且齿面接触印痕位于齿宽中部偏小端；接触迹线向小端倾斜，可增大面齿轮副的设计重合度，能够提高轮齿的强度。

从图8(a)和(b)可知：对于任意给定交点位置，斜线齿面齿轮内径1和外径2都是随着倾斜角c增大而增大，且内径增大较外径多，从而导致有效齿宽随倾斜角的增大而减小；同样，对于相同倾斜角c，交点位置从内端移向外端，即从D=−30.0 mm移动到D=30.0 mm时，斜线面齿轮内径1和外径2也随之增大，且内径增大较外径的多，使得有效齿宽减小，如图8(c)所示。

表1 齿轮副基本参数

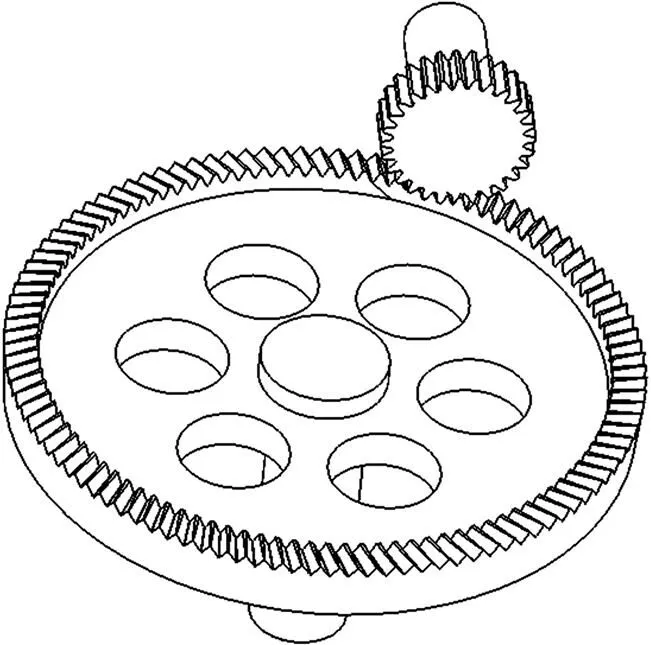
图4 斜线齿面齿轮副三维实体模型

图5 齿宽设计流程

(a) 齿根发生二次切削；(b) 齿根不发生二次切削

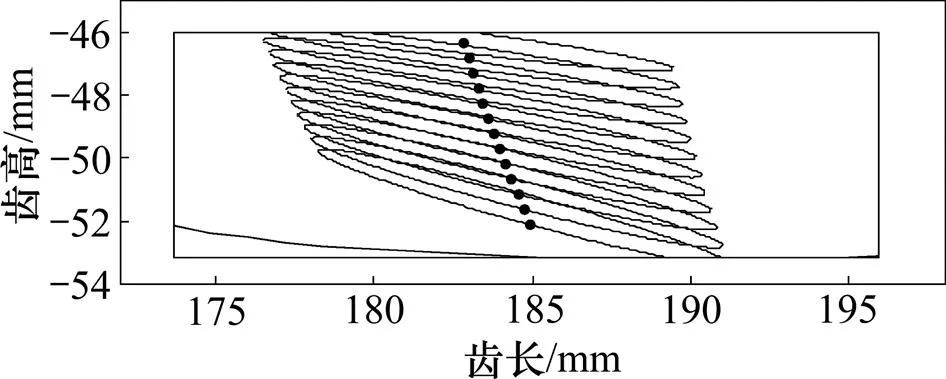
图7 齿面接触印痕

斜线齿面齿轮的最佳齿宽设计需要从倾斜角和交叉点位置这2方面分析，设计时需综合考虑斜线齿面齿轮副的实际工况、安装和轮齿强度等条件进行综合迭代优化获得，具有较高的难度，是本文后续的研究内容。

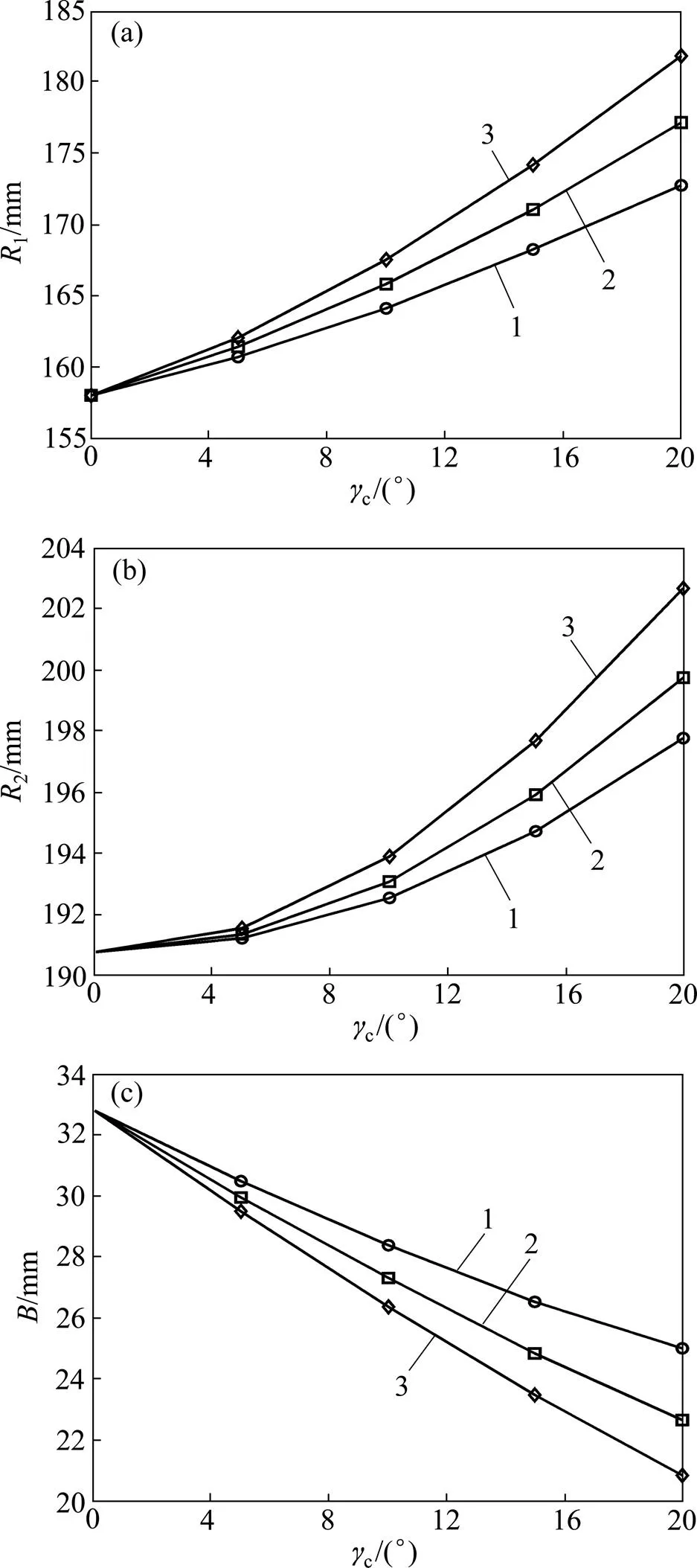
(a) 内径随倾角变化；(b) 外径随交点变化；(c)齿宽随交点、倾斜角的变化

5 结论

1) 随着倾斜角c越大，斜线齿面齿轮的内径1增大，外径2也增大，但有效齿宽减小，当c=0°时，有效齿宽达到最大，此时相当于直齿面齿轮，因此其齿形更具一般性。

2) 当交点s沿面齿轮节线移动时，获得偏置斜线齿面齿轮副；在一定的0范围内，面齿轮的有效齿宽随s从内端移向外端而减小。确定这2个参数需要综合考虑面齿轮副的实际工况、安装条件、轮齿强度等因素进行优化。

3) 减小插齿刀刀顶圆角半径c可避免出现齿根二次切削，但会引起内径增大，从而使有效齿宽减小，但其对齿宽得影响程度较小，因此应当选用较小的圆角半径，避免加工缺陷。

[1] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. New York: Cambridge University Press, 2004: 15−50.

[2] LITVIN F L, ZHANG Y, WANG J C, et al. Design and geometry of face-gear drives[J]. Journal of Mechanical Design, 1992, 114(4): 642−647.

[3] LITVIN F L, FUENTES A, HOWKINS M. Design, generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(43): 5837−5865.

[4] LITVIN F L, GONZALEZ-PEREZ I, FUENTES A, et al. Design, generation and stress analysis of face-gear drive with helical pinion[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(36): 3870−3901.

[5] ZHANG Y, WU Z. Offset face gear drives: tooth geometry and contact analysis[J]. Journal of Mechanical Design, 1997, 119(1): 114−119.

[6] 朱如鹏, 潘升材. 正交面齿轮传动中齿宽设计的研究[J]. 机械科学与技术, 1999, 18(4): 566−567. ZHU Rupeng, PAN Shengcai. Study of the design of tooth width of right shaft-angle face-gear drive[J]. Mechanical Science and Technology, 1999, 18(4): 566−567.

[7] 李政民卿, 朱如鹏. 正交面齿轮齿廓的几何设计和根切研究[J]. 华南理工大学学报(自然科学版), 2008, 36(2): 78−82. LI Zhengmingqing, ZHU Rupeng. Investation into geometrical design of tooth profile and undercut for orthogonal face gear[J]. Journal of South China University of Technology (Natural Science Edition), 2008, 36(2):78−82.

[8] 沈云波, 方宗德, 赵宁, 等. 斜齿面齿轮齿宽的设计[J]. 航空动力学报, 2008, 23(4): 754−758. SHEN Yunbo, FANG Zongde, ZHAO Ning, et al. The design of tooth face width of the face-gear drives with helical pinion[J]. Journal of Aerospace Power, 2008, 23(4): 754−758.

[9] 李大庆, 邓效忠, 魏冰阳, 等. 偏置斜齿面齿轮几何设计及齿宽特性分析[J]. 机械设计, 2011, 28(9): 59−62. LI Daqing, DENG Xiaozhong, WEI Bingyang, et al. Tooth geometry design and tooth width characteristics analysis of offset helical face-gear[J]. Journal of Machine Design, 2011, 28(9): 59−62.

[10] 魏冰阳, 袁群威, 吴聪. 偏置正交面齿轮的几何设计及三维造型[J]. 河南科技大学学报(自然科学版), 2012, 22(3): 8−11. WEI Bingyang, YUAN Qunwei, WU Cong. Tooth geometry design and three-dimension modeling of offset orthogonal face-gear[J]. Journal of Henan University of Science and Technology (Natural Science), 2012, 22(3): 8−11.

[11] 姬存强, 魏冰阳, 邓效忠, 等. 正交面齿轮的设计与插齿加工试验[J]. 机械传动, 2010, 34(2): 58−60.JI Cunqiang, WEI Bingyang, DENG Xiaozhong, et al. Design and gear shaping experiment on orthogonal face gear[J]. Mechanical Transmission, 2010, 34(2): 58−60

[12] 李永祥, 陈国定, 袁夫彩, 等. 变位面齿轮齿宽特性的研究[J]. 机械传动, 2009, 33(4): 16−18. LI Yongxiang, CHEN Guoding, YUAN Fucai, et al. Study on the characteristics of face gear with shifting[J]. Mechanical transmission, 2009, 33(4): 16−18.

[13] 蔡香伟, 方宗德, 苏进展. 弧线齿面齿轮的几何设计和数控加工[J]. 机械科学与技术, 2012, 31(11): 1781−1785. CAI Xiangwei, FANG Zongde, SU Jinzhan. Geometry design and manufacture on NC machine for face gear with arcuate tooth[J]. Mechanical Science and Technology, 2012, 31(11): 1781−1785.

[14] CUI Yanmei, FANG Zongde, SU Jinzhan, et al. Precise modeling of arc tooth face-gear with transition curve[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1346−1351.

[15] GUINGAND M, REMOND D, de VAUJANY J P. Face gear width prediction using the DOE method[J]. Journal of Mechanical Design, 2008, 130(10): 104502.

[16] GUINGAND M, de VAUJANY J P, ICARD Y. Analysis and optimization of the loaded meshing of face gears[J]. Journal of Mechanical design, 2005, 127(1): 135−143.

[17] 周辉俊, 李政民卿, 黄鹏, 等. 基于均布载荷的正交面齿轮齿根弯曲应力计算方法研究[J]. 机械制造与自动化, 2014(1): 20−22. ZHOU Huijun, LI Zhengminqing, HUANG Peng, et al. Research on calculation method of bending stress of orthogonal face-gear tooth root based on uniform load[J]. Machine Building & Automation, 2014(1): 20−22.

[18] 靳广虎, 朱如鹏, 李政民卿, 等. 齿宽系数对面齿轮齿根弯曲应力的影响[J]. 中南大学学报(自然科学版), 2011, 42(5): 1303−1309.JIN Guanghu, ZHU Rupeng, LI Zhengminqing, et al. Impact of coefficient of tooth width on bending stress of face gear[J]. Journal of Central South University (Science and Technology), 2011, 42(5): 1302−1309.

[19] 傅则绍. 微分几何与齿轮啮合原理[M]. 东营: 石油大学出版社, 1999: 151−152. FU Zeshao. The principle of differential geometry and gear meshing[M]. Dongying: Petroleum University Press, 1999: 151−152.

[20] 袁哲俊. 刀具设计手册[M]. 北京: 机械工业出版社, 1999: 950−951. YUAN Zhejun. Tool design manual[M]. Beijing: Machinery Industry Press, 1999: 950−951.

(编辑 赵俊)

Geometry design of tooth width for a new-type face gear with tilted tooth trace

SU Jinzhan1, 2, ZHANG Kunlun1, FANG Zongde3

(1. Key Laboratory of Road Construction Technology and Equipment, Ministry of Education, Chang’an University, Xi’an 710064, China;2. Key Laboratory of Advanced Manufacture Technology for Automobile Parts, Ministry of Education, Chongqing University of Technology, Chongqing 400054, China;3. School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

In order to satisfy the need of compacted design of transmission system in aviation application, a new point-contacted face gear with tilted tooth trace and the design of tooth width were studied. The equations of shaper were derived and the generated relationship between sharper cutter and work piece was simulated, and the tooth surface of face gear can be established. By setting the limiting conditions like undercutting on root of the toe, pointing on addendum of the heel, giving depth on tooth working surface and avoiding the second cutting on the toe, the valid tooth width was determined. The influence of the titled angle and positions of cross point on the inner and outer radius and tooth width were investigated. The results show that the radius of top rounder mostly affects the second undercutting of tooth root. With the increasing of the tilted angle or moving of the crossing point from the toe to the heel, the inner and outer radii increase, while tooth width decreases.

face gear with tiled tooth trace; root undercutting; addendum pointing, second cutting; tooth width design

10.11817/j.issn.1672-7207.2017.09.015

TH132

A

1672−7207(2017)09−2363−07

2016−11−12；

2017−01−23

国家自然科学基金资助项目(51205310，51375384)；陕西省自然科学基金资助项目(2015JQ5162)；中央高校基本科研业务费专项资金资助项目(310825171003，310825161006)；汽车零部件先进制造技术教育部重点实验室开放课题资助项目(2015KLMT06) (Projects(51205310, 51375384)supported by the National Natural Science Foundation of China; Project(2015JQ5162) supported by the Natural Science Foundation of Shannxi Province; Projects(310825171003, 310825161006) supported by the Fundamental Research Founds for the Central Universities; Project(2015KLMT06) supported by the Open Fund of Key Laboratory of Advanced Manufacture Technology for Automobile Parts, Ministry of Education)

苏进展，博士，副教授，从事齿轮传动技术研究；E-mail: sujinzhan@chd.edu.cn