欠驱动自主水下航行器空间曲线路径跟踪控制研究

苗建明， 王少萍， 范磊,3， 李元

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100083; 2.中国船舶重工集团公司 第710研究所, 湖北 宜昌 443003;3.61267部队 第41分队， 北京 101114)

欠驱动自主水下航行器空间曲线路径跟踪控制研究

苗建明1,2， 王少萍1， 范磊1,3， 李元1

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100083; 2.中国船舶重工集团公司 第710研究所, 湖北 宜昌 443003;3.61267部队 第41分队， 北京 101114)

针对具有模型不确定性和输入饱和的欠驱动自主水下航行器(AUV)，提出一种基于改进反步法的简单实用三维空间曲线路径跟踪鲁棒控制器。在 Serret-Frenet 坐标系下建立了空间曲线路径跟踪误差模型，结合视线角制导和虚拟向导法，设计了基于李雅普诺夫理论和改进反步法的运动学和动力学控制器。不同于传统的积分器反步法，该方法在控制器设计中采用跟踪误差的积分来增加控制器的鲁棒性，不会增加系统的状态变量和计算量；针对设计的运动学控制器存在非因果现象的问题，借助动力学模型求解出运动学控制器表达式；针对传统反步法存在的“微分爆炸”现象及动力学控制器过于复杂的问题，采用非线性跟踪微分器对控制器进行简化。仿真结果表明：采用所设计的基于改进反步法的控制器能够实现欠驱动 AUV 在模型参数不确定性和输入饱和作用下的三维空间曲线路径跟踪控制，控制精度和鲁棒性明显优于常规反步法。

控制科学与技术； 欠驱动AUV； 空间曲线路径跟踪； 反步； 李雅普诺夫理论

Abstract: Based on the modified back-stepping technique, a simple and robust spatial curvilinear path following controller for the underactuated autonomous underwater vehicles (AUVs) with model uncertainties and input saturation is presented. A path following error dynamics model is constructed in a moving Serret-Frenet frame, and the kinematic controller and dynamic controller are developed based on line-of-sight (LOS) guidance algorithm and virtual moving target method. Differing from the traditional integrator backstepping technique, the proposed method is to introduce the integral tracking errors into the controller design to improve the robustness against the uncertainties. The dynamic model is used to solve the non-causal form caused by the coupled underactuated degrees. The nonlinear tracking differentiators (NTDs) are employed to construct the numerical solution of differential virtual control commands to tackle the problem of “explosion of terms” in the traditional back-stepping process, and the dynamic controller expressions are simplified. Simulations demonstrate that the designed controller realizes the spatial curvilinear path following control of underactuated AUV with model parameter uncertainties and input saturation, and its accuracy and robustness are more excellent than those of the traditional back-stepping control.

Key words: control science and technology; underactuated AUV; spatial curvilinear path following; back-stepping; Lyapunov’s theory

0 引言

随着自主式水下航行器(AUV)在海洋研究和开发领域的应用越来越广泛，路径跟踪控制已经成为AUV运动控制的重要技术之一[1-3]。路径跟踪是控制AUV跟踪一条满足航向要求和性能约束，且与时间无关的期望轨迹[4]。由于受到质量、可靠性、复杂性及效率等多方面的因素影响，目前大部分AUV属于欠驱动系统，加上其本身具有高度的非线性和耦合性以及加速度不可积的非完整约束等特性[5]，给运动控制带来了较大挑战。

为了解决上述问题，国内外学者对于欠驱动AUV路径跟踪控制进行了大量研究。文献[6]采用线性化方法，得到了一个局部稳定的控制器。文献[7]首次在Serret-Frenet坐标系中建立路径跟踪误差方程，基于李雅普诺夫理论和反步法设计了一个水平面内的路径跟踪控制器，但是此控制器要求AUV的初始位置和期望路径的误差小于路径的最小曲率半径。文献[8-9]采用虚拟向导的方法解除了这一限制，实现了二维平面内的全局路径跟踪控制。文献[10]采用2阶自抗扰控制方法来处理典型欠驱动的路径跟踪问题，但是没有给出控制系统稳定性的理论证明。文献[11]给出了一个基于动态面技术的控制器，有效地解决了传统反步法存在的“微分爆炸”现象，并且采用神经网络方法处理水动力参数的不确定性。为了有效抵消风、浪、流等环境的干扰，文献[12]对传统的视线角制导方法进行改进，提出了一个带有积分项的视线角制导律，主要用于直线路径跟踪。文献[13]提出了一个自适应积分视线角制导律来估计未知的侧滑角,可以用于直线或者Dubins路径[14]跟踪控制。文献[15]提出了一个改进的自适应积分视线角制导律，采用一个自适应径向基函数神经网络和一个辅助系统，结合反步法实现了无人水面船在存在不确定性和输入饱和情况下的路径跟踪控制问题。

需要指出的是，上述研究成果都局限在二维平面内，由于三维空间曲线的路径跟踪控制问题更加复杂，欠驱动的自由度也增加到两个，因此到目前为止，关于三维空间曲线路径的研究成果还相对较少。文献[16-17]将积分视线角方法扩展到有恒定海流影响的三维直线路径跟踪控制中。文献[18]基于李雅普诺夫理论和反步法提出了一个三维空间的非线性自适应控制器。文献[19]在载体坐标下基于虚拟向导法建立了路径跟踪误差模型, 采用滤波反步法实现了欠驱动AUV的三维路径跟踪控制，通过2阶滤波过程获得虚拟控制量的导数, 避免了直接对虚拟控制量解析求导的复杂过程。值得注意的是，文献[18-19]忽略了侧滑角和冲角的影响，而侧滑角和冲角的存在给路径跟踪控制器的设计带来了复杂性[5]。

基于上述考虑，针对具有模型参数不确定性的欠驱动AUV，本文采用基于改进的反步法来进行三维空间曲线路径跟踪控制器的设计。不同于传统的积分器反步法，该方法在控制器设计中采用跟踪误差的积分来增加控制器的鲁棒性，因此不会增加系统的状态变量和计算量。另外，针对传统反步法存在的“微分爆炸”和控制器过于复杂等问题，采用离散非线性跟踪微分器[20]来实时计算中间虚拟控制指令导数的数值解，避免了常规反步法直接对虚拟信号解析求导带来的“微分爆炸”问题。

1 运动控制建模及问题描述

1.1 坐标系及参数定义

坐标系及参数定义如图1所示，其中：{I}为惯性坐标系，坐标原点为海平面任一点，x轴以水下机器人的主航向为正向，z轴指向地心为正，y轴与x轴和z轴构成右手坐标系；{B}为载体坐标系，坐标原点和AUV的质心位置Q点重合，其xB轴指向AUV艏部方向，yB轴指向右舷，zB轴与xB轴和yB轴构成右手坐标系；{SF}为Serret-Frenet曲线坐标系，坐标原点为期望路径上的任意一点P，xSF轴沿路径切线方向，ySF轴为法线方向,zSF轴与xSF轴和ySF轴构成右手坐标系。

图1 空间曲线路径跟踪控制坐标系及参数定义Fig.1 Frame definitions of spatial curvilinear path following

1.2 欠驱动AUV模型

假设所研究的欠驱动AUV为零浮力，重心位于浮心正下方，忽略高于2阶的非线性水动力阻尼项，且不考虑横摇运动的影响，纵倾角小于90°，欠驱动AUV的5自由度运动学模型[21-23]和动力学模型[24]分别为

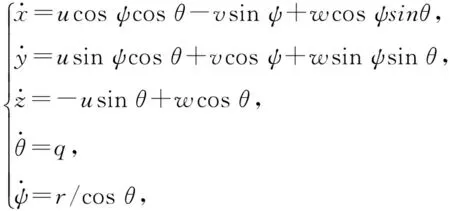
(1)

(2)

考虑到输入饱和的影响，假设-τimin≤τi≤τimax,i=u,q,r，τu、τq和τr可以用(3)式表示：

(3)

1.3 Serret-Frenet坐标系下的路径跟踪误差模型

参照文献[8,22]，在Serret-Frenet坐标系下建立欠驱动AUV的三维空间曲线路径跟踪误差模型，并采用视线角制导结合虚拟向导的方法，以避免传统横向跟踪控制方法存在的奇异性问题[7]。

如图1所示，将惯性坐标系{I}下AUV和目标路径上虚拟向导点的位置误差转换到曲线坐标系{SF}下，得到误差方程如下：

(4)

对(4)式进行求导，可得如下误差动力学方程：

(5)

忽略三维空间非线性引起的误差， 航迹角误差和潜浮角误差动力学模型[21-23]可以表示为

(6)

1.4 问题描述

2 空间曲线路径跟踪控制器设计

本文所设计的空间曲线路径跟踪控制器由视线角制导率、运动学控制器和动力学控制器3部分组成，然后针对控制器过于复杂的问题对其进行改进，下面给出每个部分的设计。

2.1 视线角制导律设计

文献[12-13]对视线角制导律进行了介绍，本文设计的制导律为

(7)

2.2 运动学控制器设计

2.2.1 姿态控制

构造李雅普诺夫函数为

(8)

对(8)式进行时间求导，并代入(6)式，可得

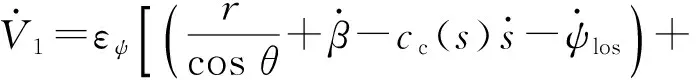
(9)

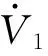
(10)

式中：k1、k2>0. 将(10)式代入(9)式可得

(11)

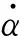
(12)

2.2.2 位置控制

构造李雅普诺夫函数为

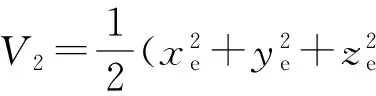
(13)

对(13)式沿误差动力学模型(5)式的轨迹对时间求导，可得

(14)

(15)

将(7)式和(15)式代入(14)式得

(16)

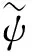
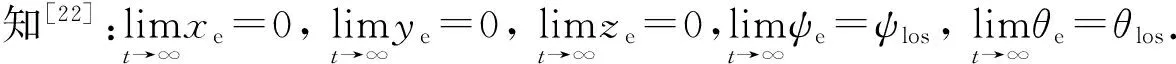
2.3 动力学控制器设计

定义虚拟航向角速度和俯仰角速度期望值为

(17)

考虑到输入饱和的影响，采用如下辅助设计系统[15]：

(18)

构造李雅普诺夫函数为

(19)

式中：k6>0.

当|φr|、|φq|、|φu|≥φμ时，将(19)式对时间求导得

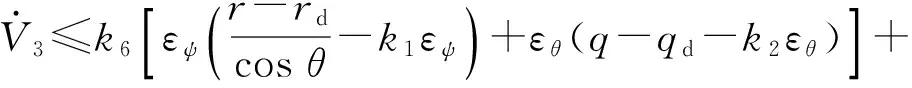
(20)

(21)

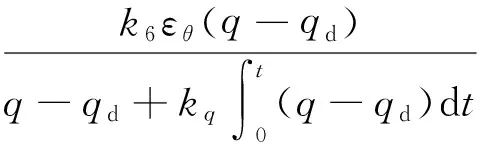
将(21)式代入(20)式得

(22)

(23)

3 控制器简化及稳定性证明

3.1 控制器简化

综上所述可以看出，上述传统反步法设计的控制器由于对虚拟控制指令直接解析求导，导致动力学控制器(23)式非常复杂，不适合实际工程应用。动态面控制方法采用1阶滤波器得到虚拟控制的数值解有效解决了“计算膨胀”的问题[11,21]，本文采用韩京清提出的非线性快速跟踪微分器[20]来实时求解虚拟航向角速度和俯仰角速度期望值导数的数值解，避免了上述非因果现象，同时简化了动力学控制器表达式。

非线性快速跟踪微分器的离散型表达式可以表示为

(24)

(25)

简化后的动力学控制器为

(26)

需要说明的是，采用非线性快速跟踪微分器对控制器简化后，必然会引入跟踪微分器的跟踪误差，下面给出其稳定性证明。

3.2 稳定性证明

考虑(1)式～(6)式描述的欠驱动AUV三维运动模型，由(7)式计算目标视线角ψlos和θlos，由(12)式计算虚拟航向角速度和俯仰角速度期望值，分别由(24)式和(25)式获取虚拟控制指令rd和qd的微分信号，采用(15)式获取虚拟向导的速度控制律，采用(26)式和(3)式计算输入力和力矩的控制律，假设参数ki>0,i=1，2，3，4，5，6，7，则有：

2)未直接驱动的横向速度v和垂向速度w一致最终有界。

证明：1)首先，重新考察李雅普诺夫函数V3，当|φr|、|φq|、|φu|≥φμ时，对(19)式沿系统轨迹对时间求导可得

(27)

式中：kv=min (k1k6,k2k6,k5-0.5,k4-0.5,k7,kφr-0.5,kφq-0.5,kφu-0.5).

解方程式(27)式可得

(28)

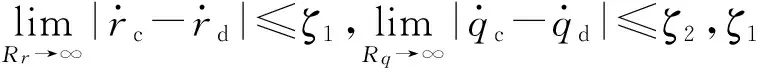
其次，重新考察李雅普诺夫函数V2，同理可以证明跟踪误差ε2=[xe,ye,ze]一致最终有界。

2)考虑如下李雅普诺夫方程：

(29)

对(27)式沿系统轨迹对时间求导，可得

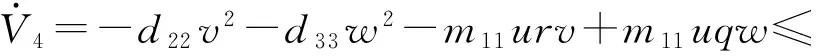
(30)

由于d22、d33>0，且m11、u、q、r均有界，根据文献[26]可知，未直接驱动的横向速度v和垂向速度w一致最终有界。

4 仿真分析

为了验证所设计控制器的有效性和鲁棒性，本文对上述控制器进行仿真分析，并与传统反步法控制器的性能进行对比。

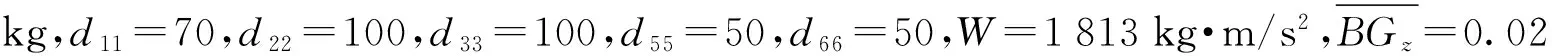
假设AUV跟踪的期望路径为：xP(μ)=μ，yP(μ)=20cos (0.05μ)，zP(μ)=20sin (0.05μ).

假设控制输入力τu的最大幅值为1 000 N，最大输入力矩τq和τr的最大幅值为500 N·m. 控制器参数设计为：k1=1，k2=1，k3=0.5，k4=1,k5=10，k6=1，k7=1，kψ=0.1，kθ=0.1，ku=0.1，kq=0.1，kr=0.1，φμ=0.001，h=0.001，kφr=kφq=kφu=10.

假设AUV参数mii(i=1,2,3,5,6) 在名义值上增加30%，dii(i=1,2,3,5,6) 在名义值上增加50%. 仿真结果如图2～图6所示，图2为AUV期望路径和实际路径，图3为Serret-Frenet坐标系下AUV和期望路径上虚拟向导之间的位置误差，图4为AUV线速度和角速度，图5为虚拟控制指令及跟踪微分器的输出，图6给出了在两种控制器作用下的控制输入。

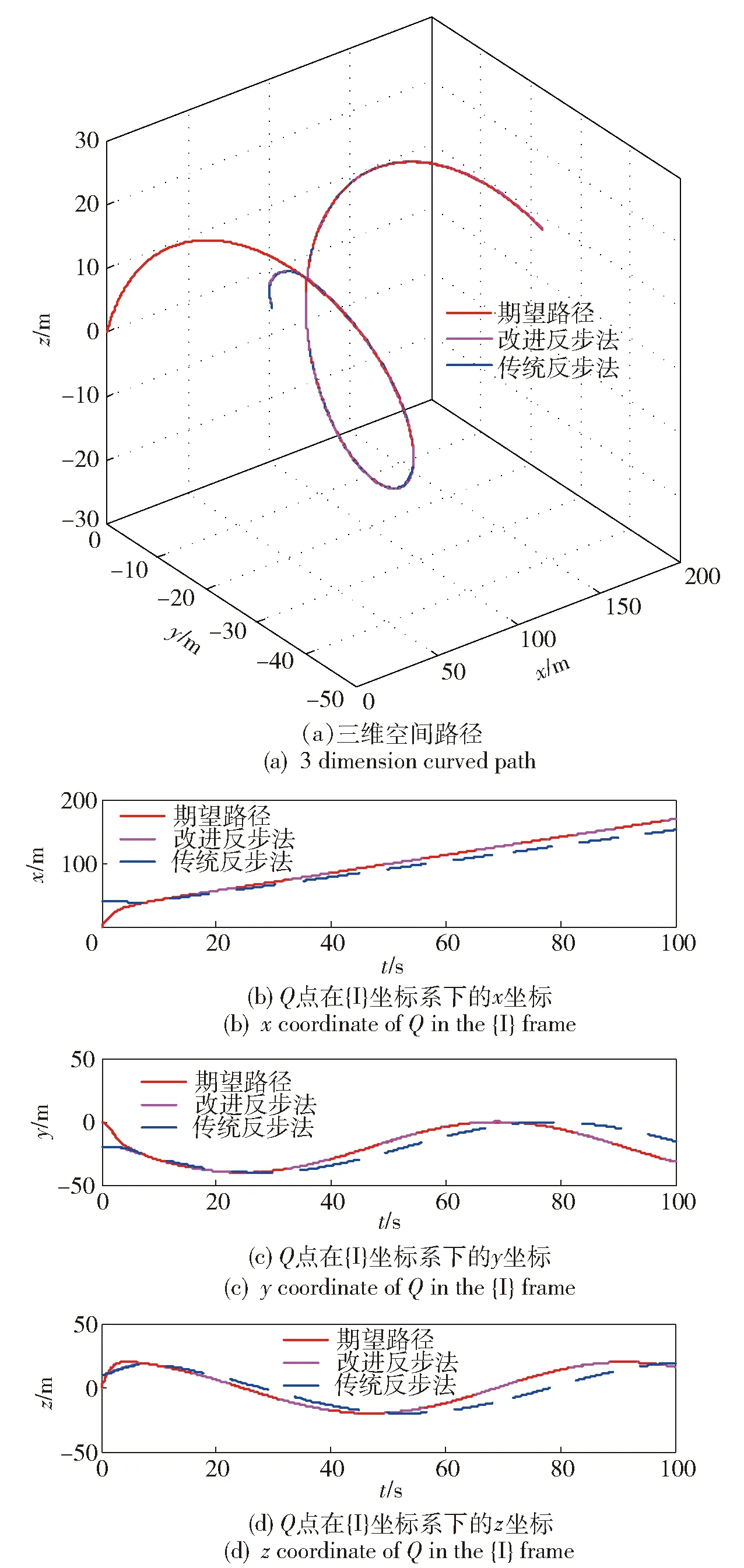
图2 AUV期望路径和实际路径Fig.2 The desired path and vehicle actual path

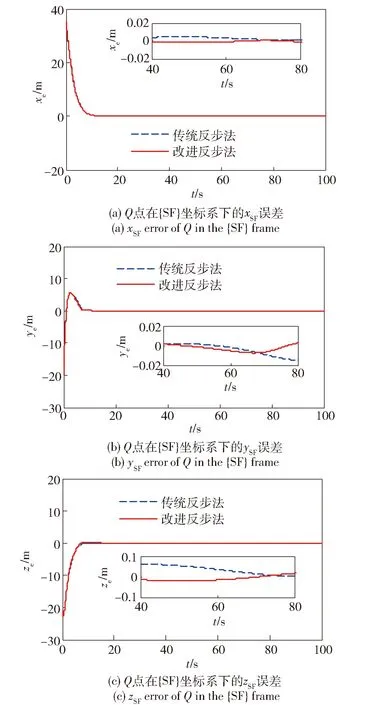
图3 AUV和期望路径上虚拟向导之间的位置误差Fig.3 Relative position errors of AUV and virtual moving target

从图2和图3中可以看出，基于改进反步法的控制器在模型参数不确定和输入饱和作用下能够实现三维空间曲线的路径跟踪控制，而基于传统反步法的控制器控制精度明显下降。图4表明AUV纵向速度在改进控制器作用下快速收敛到设定值2 m/s，而传统反步法控制器则存在一个恒定的误差。另外，从图4还可以看出，未直接驱动的横向速度v和垂向速度w均有界。图5表明所设计的非线性跟踪微分器在实现对虚拟指令快速跟踪的同时获得了其微分信号。图6表明改进的控制器控制输入始终在设定值范围内。

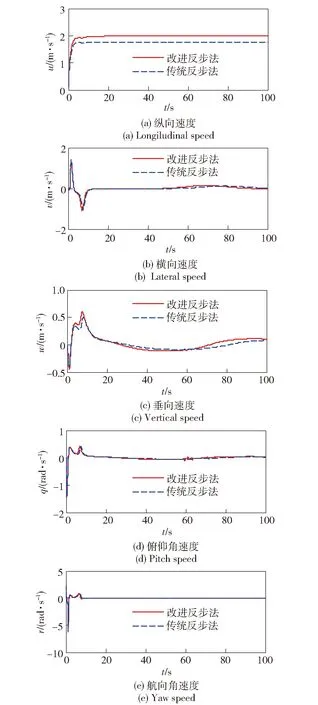
图4 AUV线速度和角速度Fig.4 Linear and angular speeds of AUV

图5 虚拟控制指令qd、rd和跟踪微分器输出的qc、rc、Fig.5 Virtual commands qd,rd, and qc,rc,, produced by nonlinear TDs

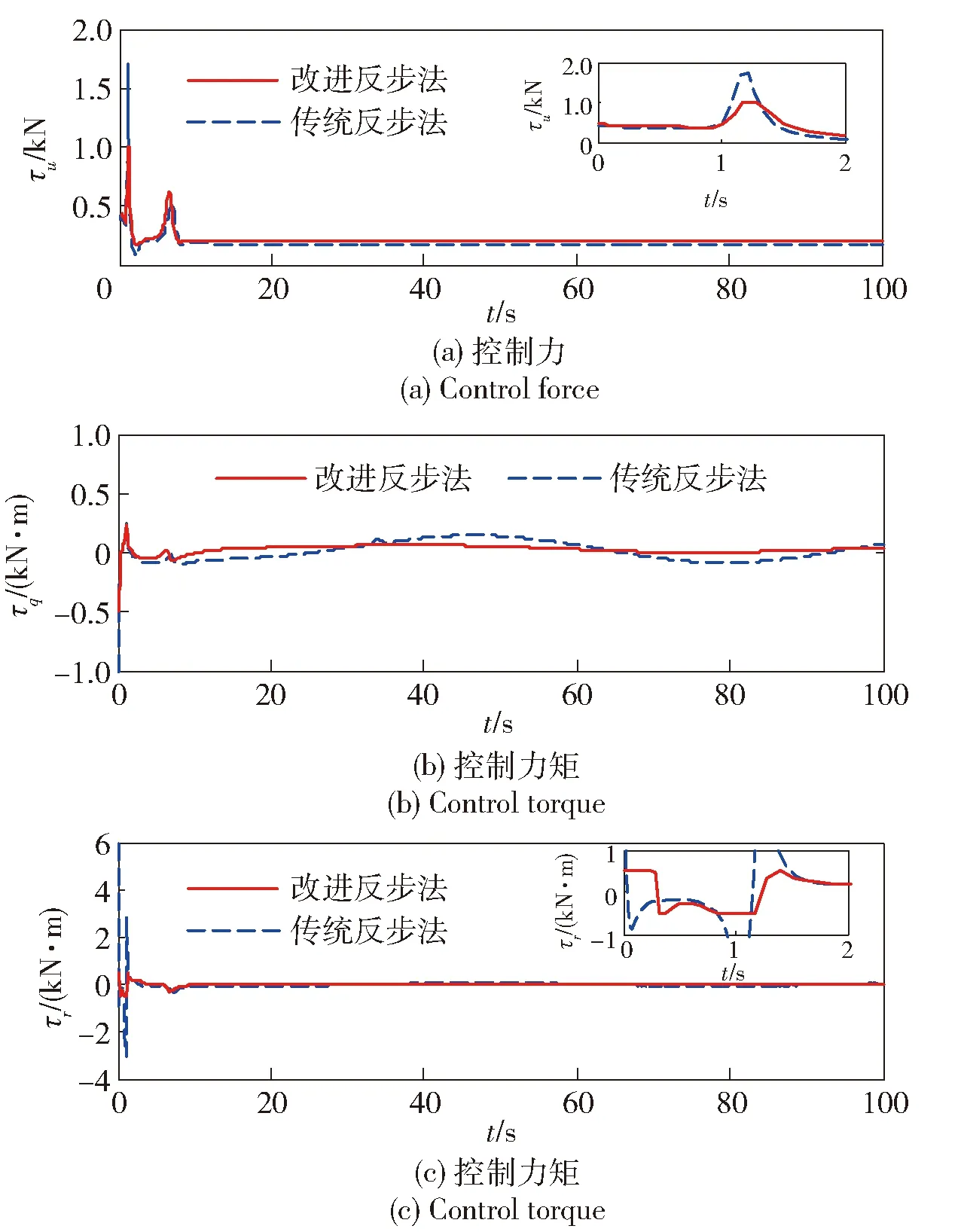
图6 控制输入力和输入力矩Fig.6 Control inputs

5 结论

本文采用一种非常简单的控制方法实现了欠驱动AUV在具有参数不确定性和输入饱和下的三维空间曲线路径跟踪控制问题。不同于传统的积分器反步法，该方法在增加控制器的鲁棒性的同时，不会增加系统的状态变量和计算量。另外，本文采用非线性跟踪微分器对控制器进行了简化。仿真结果验证了基于改进反步法的控制器能够实现欠驱动AUV在模型参数不确定性和输入饱和作用下的三维空间曲线的路径跟踪控制，并且控制精度和鲁棒性明显优于常规反步法。

References)

[1] Kohl A M, Pettersen K Y, Kelasidi E, et al. Planar path following of underwater snake robots in the presence of ocean currents[J]. IEEE Robotics and Automation Letters, 2016, 1(1): 383-390.

[2] 王芳, 万磊, 李晔, 等. 欠驱动 AUV 的运动控制技术综述[J]. 中国造船, 2010, 51(2): 227-241. WANG Fang, WAN Lei, LI Ye, et al. A survey on development of motion control for underactuated AUV[J]. Shipbuilding of China, 2010, 51(2): 227-241. (in Chinese)

[3] Shojaei K. Neural network formation control of underactuated autonomous underwater vehicles with saturating actuators[J]. Neurocomputing, 2016, 194(5): 372-384.

[4] Fossen T I. Handbook of marine craft hydrodynamics and motion control[M]. West Sussex: John Wiley & Sons, 2011.

[5] 向先波.二阶非完整性水下机器人的路径跟踪与协调控制研究[D]. 武汉:华中科技大学，2010. XIANG Xian-bo. Research on path following and coordinated control for second-order nonholonomic UUVs [D]. Wuhan：Huazhong University of Science and Technology, 2010. (in Chinese)

[6] Kaminer I, Pascoal A, Hallberg E, et al. Trajectory tracking for autonomous vehicles: an integrated approach to guidance and control[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(1): 29-38.

[7] Encarnacao P, Pascoal A, Arcak M. Path following for autonomous marine craft[C]∥5th IFAC Conference on Manoeuvring and Control of Marine Craft. Aalborg: MCMC, 2000: 117-122.

[8] Lapierre L, Soetanto D. Nonlinear path-following control of an AUV[J]. Ocean engineering, 2007, 34(11): 1734-1744.

[9] Xiang X, Lapierre L, Jouvencel B. Smooth transition of AUV motion control: from fully-actuated to under-actuated configuration[J]. Robotics and Autonomous Systems, 2015, 67: 14-22.

[10] 万磊, 张英浩, 孙玉山, 等. 欠驱动智能水下机器人的自抗扰路径跟踪控制[J]. 上海交通大学学报, 2014, 48(12): 1727-1731. WAN Lei, ZHANG Ying-hao, SUN Yu-shan, et al. ADRC path following control of underactuated AUVs[J]. Journal of Shanghai Jiao Tong University, 2014, 48(12): 1727-1731.(in Chinese)

[11] Park B S. Neural network-based tracking control of underactuated autonomous underwater vehicles with model uncertainties[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(2): 021004.

[12] Borhaug E, Pavlov A, Pettersen K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents[C]∥47th IEEE Conference on Decision and Control. Cancun, Mexico: IEEE, 2008: 4984-4991.

[13] Fossen T I, Pettersen K Y, Galeazzi R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 820-827.

[14] Dubins L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79(3): 497-516.

[15] Zheng Z, Sun L. Path following control for marine surface vessel with uncertainties and input saturation[J]. Neurocomputing, 2016, 177: 158-167.

[16] Caharija W, Pettersen K Y, Gravdahl J T. Integral LOS guidance for horizontal path following of underactuated autonomous underwater vehicles in the presence of vertical ocean currents[C]∥American Control Conference (ACC). Montreal, Canada: IEEE, 2012: 5427-5434.

[17] Caharija W, Pettersen K Y, Gravdahl J T, et al. Path following of underactuated autonomous underwater vehicles in the presence of ocean currents[C]∥Decision and Control (CDC), IEEE 51st Annual Conference on. NY, US: IEEE, 2012: 528-535.

[18] Do K D, Pan J, Jiang Z P. Robust and adaptive path following for underactuated autonomous underwater vehicles[J]. Ocean Engineering, 2004, 31(16): 1967-1997.

[19] 王宏健, 陈子印, 贾鹤鸣, 等. 基于滤波反步法的欠驱动 AUV 三维路径跟踪控制[J]. 自动化学报, 2015, 41(3): 631-645. WANG Hong-jian, CHEN Zi-yin, JIA He-ming, et al. Three-dimensional path-following control of underactuated autonomous underwater vehicle with command filtered backstepping[J]. Acta Automatica Sinica, 2015, 41(3): 631-645.(in Chinese)

[20] 韩京清. 自抗扰控制技术(估计补偿不确定因素的控制技术[M]. 北京:国防工业出版社, 2009:66-73. HAN Jing-qing.Active disturbance rejection control technique-the technique foe estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press,2009: 66-73.(in Chinese)

[21] Chwa D. Global tracking control of underactuated ships with input and velocity constraints using dynamic surface control method[J]. IEEE Transactions on Control Systems Technology, 2011, 19(6): 1357-1370.

[22] Qi X. Spatial target path following control based on Nussbaum gain method for underactuated underwater vehicle[J]. Ocean Engineering, 2015, 104: 680-685.

[23] 贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动 UUV 三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314. JIA He-ming, ZHANG Li-jun, CHENG Xiang-qin, et al. Three-dimensional path following control for an underactuated UUV aased on aonlinear iterative sliding mode[J]. Acta Automatica Sinica, 2012, 38(2): 308-314.(in Chinese)

[24] Pettersen K Y, Egeland O. Time-varying exponential stabilization of the position and attitude of an underactuated autonomous underwater vehicle[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 112-115.

[25] Miao J M, Wang S P, Zhao Z P, et al. Spatial curvilinear path following control of underactuated AUV with multiple uncertainties[J]. ISA Transactions, 2017,67:107-130.

[26] Khalil H K. Nonlinear systems[M]. 3rd ed. NY, US: Pearson Education, 2002.

SpatialCurvilinearPathFollowingControlofUnderactuatedAUV

MIAO Jian-ming1,2, WANG Shao-ping1, FAN Lei1,3, LI Yuan1

(1.School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China；2.No. 710 Research Institute, China Shipbuilding Industry Corporation, Yichang 443003, Hubei, China；3. 41th Detachment, Unit 61267 of PLA, Beijing 101114, China)

TP242.3

A

1000-1093(2017)09-1786-11

10.3969/j.issn.1000-1093.2017.09.016

2017-01-06

国家“973”计划项目(2014CB046402)；国家自然科学基金项目(51575019)

苗建明(1979—), 男，高级工程师, 博士研究生。E-mail: sxmjm@126.com

王少萍(1966—), 女, 教授，博士生导师。E-mail: shaopingwang@vip.sina.com