一种用于水下小尺度运动阵列的目标波达方向估计方法

郭拓， 王英民， 张立琛

(西北工业大学 航海学院， 陕西 西安 710072)

一种用于水下小尺度运动阵列的目标波达方向估计方法

郭拓， 王英民， 张立琛

(西北工业大学 航海学院， 陕西 西安 710072)

为解决水下小尺度运动阵列对目标定位的孔径和样本不足问题，采用合成孔径方法实现孔径的扩展。通过分析相干信源情况下不同阵元数与样本数之比时样本协方差矩阵的谱分离特性，提出采用小快拍的主特征空间目标波达方向估计方法。研究结果表明：仿真实验中，阵元数与样本数之比为5时，该方法依然可以正确分辨4个目标；水池试验中，阵元数与样本数之比为4.8时，该方法同样可以准确分辨3个相邻目标。该方法不需要先验信息如信源个数等，解决了小尺度运动阵列在实际应用时所暴露的孔径和样本方面的固有局限，可满足实际应用需求。

声学； 小尺度运动阵； 主特征空间； 波达方向估计； 小快拍

Abstract: The underwater small-scale moving array is limited by its small aperture and sample size for direction of arrival (DOA) estimation of coherent target. The passive synthetic aperture technique is used to solve the problem of insufficient aperture. The spectral separation of sample covariance matrix is stu-died in the case of coherent target. A DOA estimation method for coherent target based on main feature space is proposed, which uses small snapshots. In the simulation, the proposed method can still distinguish the four targets correctly when the ratio of the number of sensors to the number of samples is 5; in the water tank experiment, the above ratio is 4.8, and it can identify three adjacent targets clearly. The proposed method can achieve better resolution for coherent targets in small samples, which meets the application needs of small-scale motions array of targeting, and requires no priori information of signal source number.

Key words: acoustics; small-scale moving array; main feature space; DOA estimation; small snapshot

0 引言

小尺度声纳基阵由于其体积小、成本低、基阵校准和使用方便，广泛应用于鱼雷、水雷、水下无人航行器等小尺度安装平台上。但该声纳平台的运动特性导致在信号的局部平稳过程中所获得的样本数较小，小尺度阵即阵列孔径较小，因此基于小尺度运动阵列的目标波达方向(DOA)估计成为一个关键问题。

DOA估计作为阵列信号处理的一个重要分支，已经广泛用于雷达、声纳、通信、无源定位等多个领域[1-3]。阵列DOA估计经过几十年的发展，已经形成了两类技术，即基于波束形成技术和基于子空间分解技术。其中：基于波束形成技术的典型方法有常规波束形成器(CBF)和最小方差无畸变响应(MVDR)波束形成器；基于子空间分解技术的经典方法[4]是多重信号分类(MUSIC)算法。

上述传统DOA估计算法大都基于孔径较大的阵列，其估计性能随着阵列孔径的减小会迅速下降，且都需要估计基阵的统计协方差矩阵。在实际数据处理中都以样本协方差矩阵代替统计协方差矩阵，在小样本情况下如此估计出的统计协方差矩阵误差很大，会导致DOA估计算法失效。特别是对于相干目标，经典的高分辨方法如MUSIC随着信号相干程度的增加，空间分别率逐渐下降，甚至完全失效。因此针对水下小尺度运动阵列对相干目标DOA估计成为亟待解决的问题，以实现在小孔径情况下采用小样本进行方位估计。

针对小样本数问题，为了获得与统计协方差矩阵更加相近的样本协方差矩阵，通常情况下会对样本协方差矩阵进行修正，目前已经发展了很多修正方法，如：1)对角加载方法[5]、收缩因子方法[6-8]，二者都是通过对样本协方差矩阵的特征值进行加权操作以改进其性能；2)前后向平均[9]和空间光滑技术[10]，通过移动窗口虚拟出更多的快拍，以改进样本协方差矩阵估计；3)伪随机噪声再采样技术[11-13]，通过人为生成伪随机噪声信号加在接收到的信号上，以改进样本协方差矩阵估计；4)子空间泄露分析方法[14]，通过MUSIC算法的估计改进所需的样本协方差矩阵，以减少样本协方差矩阵方位估计时信号子空间的泄漏。上述方法的思路都是设法改进样本协方差矩阵，以使其与大样本时的样本协方差矩阵更加相近，但没有考虑样本协方差矩阵与样本数的关系，以及样本数不同时协方差矩阵本身所具有的不同特性。

本文首先采用被动合成孔径技术进行阵列的孔径扩展，解决阵列的孔径不足问题；对于小样本问题将打破上述通过改进样本协方差矩阵来改进方位估计的思路，而是通过研究不同快拍时样本协方差矩阵本身具有的一些特性如谱的分离特性，提出基于小样本协方差矩阵的主特征空间DOA估计方法。

1 阵列接收信号模型

如图1所示，水平线阵由N个阵元组成，假设有D个相互独立的平面波入射，阵列第k次快拍X(k)为

X(k)=A(θ)S(k)+N(k),

(1)

式中：X(k)=[x1(k),x2(k),…,xN(k)]T；A(θ)为阵列流形矩阵，A(θ)=[a(θ1),a(θ2),…,a(θD)]，θj为第j个平面波的水平入射角，a(θj)=[1,ej2πdsin (θj)/λ,…,ej2π(N-1)dsin (θj)/λ]为第j个入射平面波的导向向量,d为阵元间距，其值等于波长λ的一半 ；S(k)=[s1(k),s2(k),…,sD(k)]T,sj(k)为第j个平面波信号的第k次快拍；N(k)=[n1(k),n2(k),…,nN(k)]为阵列接收到的加性高斯白噪声，ni(k)为第i个阵元接收到的噪声。

图1 阵列接收信号模型Fig.1 Array signal model

当信号被假设具有零均值时，阵列接收信号的协方差矩阵R=E[X(k)XH(k)]，即协方差矩阵需要通过求集总平均得到。而实际应用中只能得到有限的采样数据，如有M次观测样本X(1),X(2),…,X(M)，则用这M个样本估计的采样协方差矩阵为

(2)

2 基于主特征空间的DOA估计方法

2.1 样本协方差矩阵特征的谱分离特性

令y=N/M，y表示阵元数与样本数之比，文献[15-17]采用随机矩阵理论研究样本协方差矩阵谱的极限分布，研究表明样本协方差矩阵具有谱分离特性。文献[18]详细研究了样本协方差矩阵的谱分离特性，并给出样本协方差矩阵的谱随y变化的特点，研究了y为1.00(样本数等于阵元数)、y为0.01(样本数是阵元数的100倍)以及在y由1.00逐渐变小至0.01的过程中的特征值分布表现形式，研究发现：特征值分布表现为一簇一簇的，每簇中有几个大小相近的特征值，其中每个簇的中心渐近于统计协方差矩阵R的一个真实特征值。每个簇的大小取决于y，即估计R的样本数，如果每个阵元所取的样本数小，则每个簇将会很大，的许多特征值将汇集在一个簇中，无法分离；反之，如果每个阵元所取的样本数足够大，则每个簇只对应R的一个真实特征值，这样R的谱就得到很好的分离。

仿真实验采用30个阵元，4个相干目标，噪声为高斯白噪声，可得如图2所示的特征值随不同y的变化曲线。由图2可知：当y很小时，即样本数远远大于阵元数即y很小时，的特征值会在最大特征值序数处陡峭升高，即最大特征值远大于其他特征值；当y较大时，特征值不再陡峭升高，紧邻最大特征值处还有较大的特征值。图2中特征值随y变化的特征，是相干源情况下样本协方差谱分离特性的具体体现。从子空间的角度来解释上述相干源时的谱分离特性，当样本数远远大于阵元数即y很小时，样本协方差矩阵得到较好的估计，相干信号的信息全部集中在一个最大特征值所对应的子空间上；当y较大时，样本协方差矩阵没有得到很好的估计，此时信号子空间发生了泄漏，使得除了最大特征值之外还出现一些连续的较大特征值，但是总体而言所有相干信号的主要信息仍然集中于最大特征值所对应的子空间中。本文将这个最大特征值所对应的子空间称为主特征空间，而不是MUSIC算法所假设的那样，即信号子空间就是s个信源所对应的s个较大特征值所构成的空间。通过上述对相干源情况下不同样本数时谱分离特性的仿真实验与分析，显然信号信息主要集中在主特征空间而不是MUSIC算法所使用的s个较大特征值构成的空间，从而很好地解释了MUSIC算法对相干目标DOA估计时失效的原因。

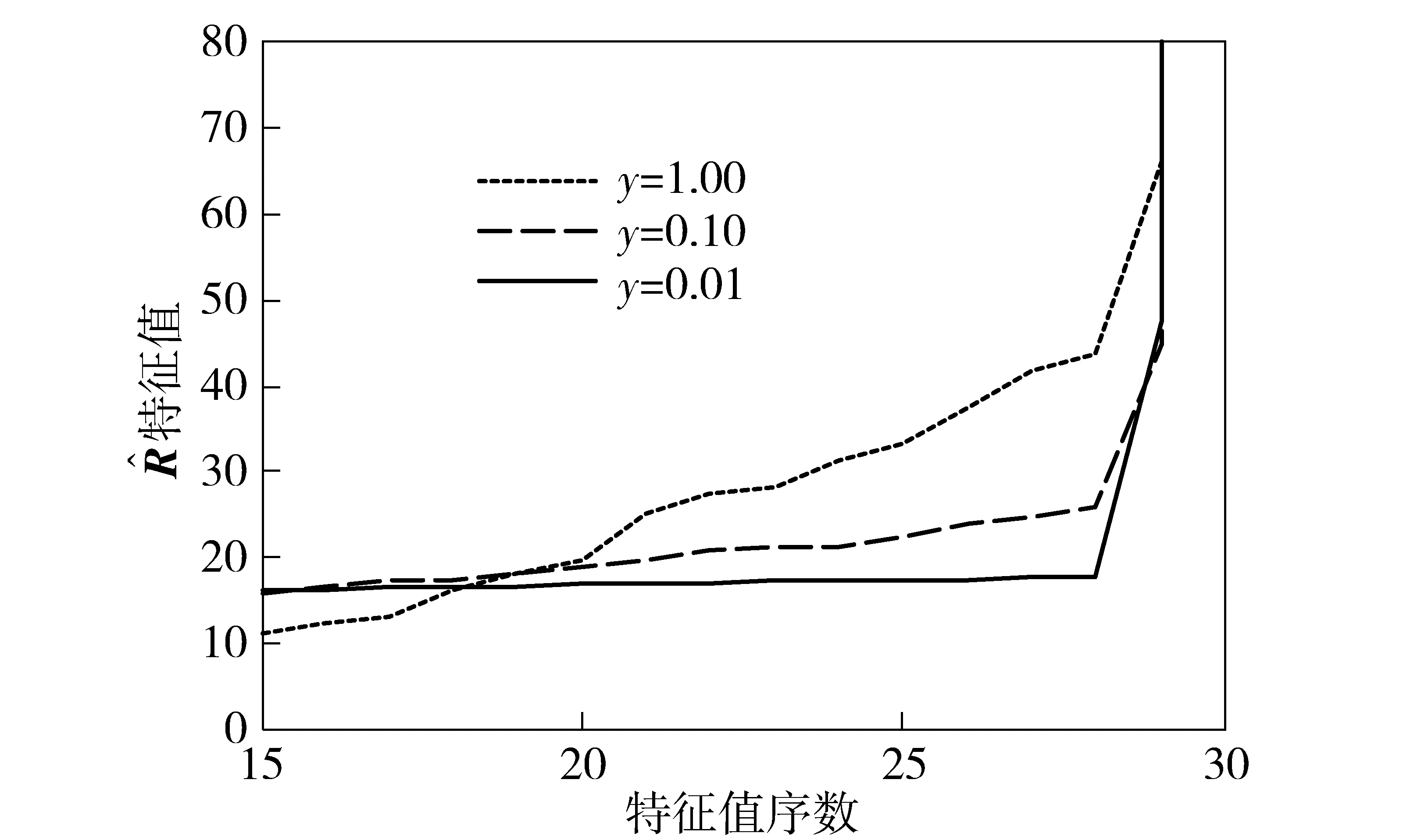
图2 相干目标的谱分离性Fig.2 Spectral separation of coherent target

综上所述，无论快拍数大小，目标为相干信号时其样本协方差矩阵具有很好的谱分离特性，下面将基于谱分离特性提出相干信号的目标DOA估计方法。

2.2 基于被动合成孔径的主特征空间DOA估计方法

被动合成孔径声纳有几种经典算法，本文采用较实用的扩展拖曳阵测量(ETAM)方法[19]。

假设目标是窄带声源，f0为声源频率，则目标信号可表示为s(tg)=Aexp (j2πf0tg)，A为信号幅度，tg为第g个时刻点。tg时刻第i个阵元接收到θj的信号可表示为

(3)

式中：f为目标频率；c为水下声速；εi,g为噪声。

由于阵列与目标之间的相对运动，接收到的目标频率f为

f=f0(1±vsinθj/c)，

(4)

式中：v为阵列与目标之间的相对运动速度。

将(4)式代入(3)式，得

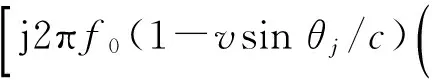
(5)

将(5)式化简，略去sinθ的2阶项，整理得

(6)

如果阵列不移动，则tg+τ时刻(τ为时间间隔)第i个阵元接收到的信号可表示为

(7)

如果选择合适的间隔时间τ，使得vτ=qd，即运动的距离正好等于q个阵元间距d，则tg+τ时刻第i个阵元接收到的信号变换为

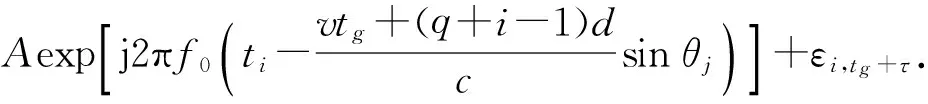
(8)

而tg时刻第i+q个阵元接收到的信号为

(9)

比较(8)式与(9)式发现，二式只相差一个相位补偿项，说明可以通过第i个阵元的运动来虚拟出tg时刻的第i+q个阵元。当阵列匀速运动时，时刻tg的第N-q+p个阵元与时刻tg+τ的第p个阵元在空间中同一个位置，即不同的阵元在不同的时刻接收空间相同位置上的信号。N-q为两个时刻重叠阵元数，利用N-q个重叠阵元计算两个时刻的相位补偿，q即为一次合成孔径虚拟出的阵元数，N为阵列物理阵元个数，经过u次合成则可以虚拟出q×u个阵元，经过u次孔径合成的总阵元数为N+q×u.

经过虚拟孔径合成后，物理阵和虚拟阵列接收到的信号可表示为

Xe(k)=
[x1(k),x2(k),…,xN(k),xN+1(k)，…，xN+q×u(k)]T.

(10)

经ETAM算法进行孔径扩展后的实际使用样本协方差矩阵可以用(11)式估计：

(11)

(12)

式中：λi为e的特征值；ei为该特征值所对应的特征向量；E为以所有特征向量按列排所构成的特征矩阵。

2.1节已将样本协方差矩阵的最大特征值所对应的空间定义为主特征空间，此处定义只包括最大特征值所对应的空间，并非主特征空间只包含最大特征值所对应的空间，也可以根据信源的特点扩展主特征空间。定义e可以划分为

(13)

式中：λm为主特征空间的特征值；em为与其对应的特征向量；Em为主特征空间特征向量构成的矩阵；Eo为特征空间E中去除主特征后的特征信息矩阵。

根据子空间理论，信号子空间与噪声子空间正交，且导向向量张成的空间与信号子空间张成的空间是同一空间，即Ena(θ)=0，Esa(θ)=1，其中En为噪声子空间，Es为信号子空间。

主特征空间中包含的主要是信号信息，即主特征子空间Em中主要包含的是Es空间的信息，当样本数较小时会发生子空间泄漏，有部分En的信息进入Em，使Ema(θ)=1，则arccos(Ema(θ))=0，故定义其倒数为主特征空间方法的方位谱估计，即

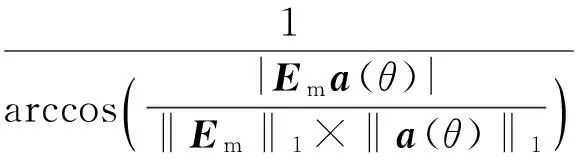
(14)

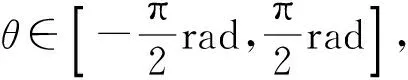
下面将合成孔径后，采用主特征空间方法进行方位估计的方法简称为ETAM-MFS.

3 仿真实验

通过数值仿真模拟水下小尺度运动阵列目标定位，首先采用被动合成孔径算法ETAM进行孔径扩展，然后采用主特征空间DOA估计方法估计目标方位。仿真采用一个半波长均匀分布的6元线阵模拟小尺度阵列，阵列运动速度为0.07 m/s，入射的信号为4个远场窄带信号，频率为6.25 kHz，采样频率50 kHz，4个信号的入射角分别为-20°、-10°、0°、10°，信噪比皆为0 dB，噪声为复高斯白噪声，快拍数取6，ETAM算法经过8次合成得到24个虚拟阵元，总线阵为30个阵元，阵元数与样本数之比y为5.

图3为CBF算法给出的目标DOA估计，图4为MVDR算法给出的目标DOA估计，图5为MUSIC算法给出的目标DOA估计，图6为ETAM-MFS方法给出的目标DOA估计。由图3～图6可以发现，在30个阵元、6快拍情形下，CBF方法、MVDR方法与MUSIC方法都不能正确估计出目标方位，而ETAM-MFS方法可以正确分辨出目标方位。由此可见，本文提出的方法可以在小快拍情况下很好地分辨相干目标，且不需要像MUSIC算法那样预先拥有目标个数的先验信息，这是相干源时样本协方差矩阵的谱分离特性带来的好处，即信号信息全部集中于主特征空间，只有很少的信号泄漏于其他空间。

图3 CBF方法DOA估计Fig.3 DOA estimation of CBF

图4 MVDR方法DOA估计Fig.4 DOA estimation of MVDR

图5 MUSIC方法DOA估计Fig.5 DOA estimation of MUSIC

图6 ETMA-MFS方法DOA估计Fig.6 DOA estimation of ETMA-MFS

4 水池试验

为了验证所提算法在小尺度运动阵列小样本的情况下能够分辨相干目标，在消声水池(长20 m, 宽8 m，深7 m，6面消声)进行了相关试验。试验采用由6个水听器组成的均匀线阵，设计频率为6.25 kHz，水平布放于水下2.5 m深处，阵元间距为半波长0.12 m，阵列匀速运动速度为0.07 m/s，使用电机匀速拉动；3个发射源发射频率均为6.25 kHz的连续波信号，与接收阵在同一深度，3个源按远场条件布放，与阵列形成的角度分别为24°、33°、44° ；采样频率为50 kHz. 首先采用被动合成孔径算法ETAM合成6次，共得到24个阵元，快拍数取5，阵元数与样本数之比y为4.8. 试验系统如图7所示，试验现场如图8所示。

图7 水池试验系统Fig.7 Water tank experimental system

图8 水池试验现场Fig.8 Water tank experimental site

图9～图12为采用被动合成孔径ETAM算法得到24个虚拟阵元后，分别使用CBF方法、MVDR方法、MUSIC方法与MFS方法得到的目标DOA估计，图中目标的真实方位用黑点标出。由图9可知，CBF方法不能清晰分辨3个目标，且具有明显的方位误差，其中物理阵所对应的是实际物理6个阵元没有进行合成孔径得到的目标DOA估计。由图10可知，MVDR方法只能估计出3个目标中的2个。由图11可知，MUSIC方法也只能估计出3个目标中的2个。从图12可以发现，ETAM-MFS算法可以很好地分辨3个目标，且没有方位误差。与其他3种方法相比，首先，本文所提出的方法不需要做协方差矩阵求逆运算，减少了计算量；其次，不需要先验信息如信源个数；最后，最重要的是，本文所提出的方法在小样本情形下表现优异，能够准确分辨目标。

图9 水池试验合成孔径前后DOA估计对比Fig.9 DOA estimations before and after synthetic aperture in water tank experiment

图10 水池试验MVDR方法DOA估计Fig.10 DOA estimation of MVDR in water tank experiment

图11 水池试验MUSIC算法DOA估计Fig.11 DOA estimation of MUSIC in water tank experiment

图12 水池试验ETAM-MFS方法DOA估计Fig.12 DOA estimation of ETAM-MFS in water tank experiment

5 结论

为解决水下小尺度运动阵列的目标DOA估计中的孔径和样本不足问题，本文首先采用被动合成孔径算法ETAM弥补小尺度阵的孔径不足，然后在对样本协方差矩阵谱分离特性分析的基础上提出了小快拍主特征空间DOA估计方法。在分析相干目标样本协方差矩阵的谱分离特性时，还得出了MUSIC算法对相干目标分辨失效的原因。通过仿真实验和水池试验，将本文所提出的方法与传统DOA估计方法(CBF算法、MVDR算法以及MUSIC算法)进行了对比，结果发现：当快拍数很小时，试验中阵元数与快拍之比接近5时，该方法依然可以准确地分辨多个目标，而其他3种方法或是出现多个伪目标或是有目标不能估计出。

本文所提出的方法实现了水下小尺度运动阵列的目标方位估计，主要体现在：1)通过合成孔径克服了小尺度阵列孔径的不足；2)能够实现小快拍相干目标的DOA估计，可以很好地弥补MUSIC算法的缺陷，且不需要先验信息如信源个数。该方法适合于水下小尺度运动阵列目标定位的应用需求，期望能在无人水下航行器、鱼雷等应用中有很好的应用前景。

References)

[1] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4):67-94.

[2] 吴振, 戴继生, 朱湘临, 等. 互耦效应下一种基于实值稀疏表示的波达方向估计算法[J]. 兵工学报, 2015, 36(2):294-298. WU Zhen,DAI Ji-sheng, ZHU Xiang-lin, et al. A real-valued sparse representation method for DOA estimation with unknown mutual coupling[J]. Acta Armamentarii, 2015, 36(2):294-298.(in Chinese)

[3] 邹吉武, 孙大军. 线阵双基地声纳波束零点形成MUSIC算法[J]. 兵工学报, 2010, 31(3):364-368. ZOU Ji-wu, SUN Da-jun. MUSIC algorithm of beam null forming on linear array of bi-static sonar[J]. Acta Armamentarii, 2010, 31(3):364-368.(in Chinese)

[4] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004:2-5. WANG Yong-liang, CHEN Hui, PENG Ying-ning, et al. Theory and algorithm of spatial spectrum estimation[M]. Beijing: Tsinghua University Press, 2004:2-5.(in Chinese)

[5] Carlson B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace Electronic Systems, 1988, 24(4):397-401.

[6] Chen Y, Wiesel A, Eldar Y C, et al. Shrinkage algorithms for MMSE covariance estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(10):5016-5029.

[7] Tong J, Schreier P J, Guo Q, et al. Shrinkage of covariance matrices for linear signal estimation using cross-validation[J]. IEEE Transactions on Signal Processing, 2016, 64(11):2965-2975.

[8] Auguin N, Morales-Jimenez D, Mckay M, et al. Robust shrinkage M-estimators of large covariance matrices[C]∥Proceedings of 2016 IEEE Statistical Signal Processing Workshop. Palma de Mallorca, Baleares, Spain:IEEE, 2016:1-4.

[9] Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1989, 37(1):8-15.

[10] Pal P, Vaidyanathan P P. A novel array structure for directions-of-arrival estimation with increased degrees of freedom[C]∥Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing. Dallas, TX, US:IEEE, 2010:2606-2609.

[11] Gershman A B, Bohme J F. Improved DOA estimation via pseudo-random resampling of spatial spectrum[J]. IEEE Signal Processing Letters, 1997, 4(2):54-57.

[12] Vasylyshyn V. Removing the outliers in root-MUSIC via pseudo-noise resampling and conventional beamformer[J]. Signal Processing, 2013, 93(12):3423-3429.

[13] Qian C, Huang L, So H C. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Processing Letters, 2014, 21(2):140-144.

[14] Shaghaghi M, Vorobyov S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Tran-sactions on Signal Processing, 2015, 63(12):3251-3265.

[15] Bai Z D, Silverstein J W. No eigenvalues outside the support of the limiting spectral distribution of large-dimensional sample covariance matrices[J]. Annals of Probability, 1998, 26(1):316-345.

[16] Bai Z D, Silverstein J W. Exact separation of eigenvalues of large dimensional sample covariance matrices[J]. Annals of Probability, 1999, 27(3):1536-1555.

[17] 李华, 白志东, 肖玉山. 大维随机矩阵的渐进特征[J]. 东北师大学报:自然科学版, 2014, 46(4):1-8. LI Hua, BAI Zhi-dong, XIAO Yu-shan. The asymptotic properties of the large dimension random matrix[J]. Journal of Northeast Normal University:Natural Science Edition, 2014, 46(4): 1-8.(in Chinese)

[18] Mestre X, Lagunas M. Modified subspace algorithms for DoA estimation with large arrays[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 598-614.

[19] Stergiopoulos S, Sullivan E J. Extended towed array processing by an overlap correlator[J]. Journal of the Acoustical Society of America, 1989, 86(1): 158-171.

NovelTargetDirection-of-arrivalEstimationMethodforUnderwaterSmall-scaleMovingArray

GUO Tuo, WANG Ying-min, ZHANG Li-chen

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China)

TB566

A

1000-1093(2017)09-1779-07

10.3969/j.issn.1000-1093.2017.09.015

2017-01-17

国家自然科学基金项目(61401362)

郭拓(1986—)，男，博士研究生。E-mail:guotuonwpu@126.com

王英民(1963—)，男，教授，博士生导师。E-mail:ywang@nwpu.edu.cn