基于混合自适应遗传算法的相控阵雷达任务调度

张浩为， 谢军伟， 张昭建， 宗彬锋， 陈唐军

(1.空军工程大学 防空反导学院， 陕西 西安 710051；2.94710部队， 江苏 无锡 214000；3.94921部队， 福建 晋江 362200)

基于混合自适应遗传算法的相控阵雷达任务调度

张浩为1， 谢军伟1， 张昭建1， 宗彬锋2， 陈唐军3

(1.空军工程大学 防空反导学院， 陕西 西安 710051；2.94710部队， 江苏 无锡 214000；3.94921部队， 福建 晋江 362200)

针对相控阵雷达任务调度NP难题，提出一种混合自适应遗传算法进行求解。在构建相控阵雷达任务调度优化模型的基础上，通过混沌理论优化初始种群，采取精英保留和混合排名的选择策略以及设计自适应的交叉、变异算子来提升算法的搜索性能；在自适应遗传算法的框架下，提出启发式脉冲交错算法，以利用雷达任务中的等待期来交错执行其他任务的发射期或接收期。仿真结果表明：相比于基于遗传算法的调度方法，改进算法的搜索效率更高、结果更优；相比于传统启发式算法，改进算法的调度成功率、时间利用率和实现价值率均得到了提升，并有效降低了时间偏移率。

兵器科学与技术； 相控阵雷达； 调度； 自适应遗传算法； 混沌理论； 脉冲交错

Abstract: A hybrid adaptive genetic algorithm is proposed for the task scheduling of phased array radar. An optimal scheduling model for phased array radar is established. The performance and efficiency of the algorithm are improved by optimizing the initial population by the chaos theory, adopting the selection strategy of elite reservation and mixed ranking, and designing the adaptive crossover and mutation operators. A heuristic pulse interleaving algorithm is presented based on the adaptive genetic algorithm. It could utilize the waiting period in a task to execute the transmitting period or receiving period of other task. The simulated results demonstrate that the proposed algorithm provides better results and search solutions more quickly than the genetic algorithm. Moreover, compared with the heuristic scheduling algorithm, the proposed algorithm improves the scheduling success ratio, time utilization ratio and high value ratio, and decreases the average time shift ratio efficiently.

Key words: ordnance science and technology； phased array radar; scheduling; adaptive genetic algorithm; chaos theory; pulse interleaving

0 引言

相控阵雷达因其对时间资源的高效利用，可以实现微秒量级的波束捷变，进而同时承担搜索、跟踪和制导等多种任务。因此，研究在时间资源有限[1]的前提下实现任务的最优调度，对充分发挥相控阵雷达的多功能潜力具有重要意义。

大量研究结果表明，相控阵雷达中的任务调度问题属于NP难题，最优解难以获得。目前，解决该类问题的方法可分为启发式算法和智能算法。前者通过预先设定的优先级规则，对满足条件的任务优先进行调度。典型的有：截止期最早最优先(EDF)算法[2-3]、价值最高最优先算法[4-5]等。但在调度过程中，优先级仅由任务的单个属性来确定是不够的。文献[6-7]依据任务序列和相关参数，将请求任务划分为多个队列，在每个队列中运用先入先出(FIFO)原则或截止期优先原则进行调度。文献[8-12]综合了任务的工作方式和截止期两种因素，以确定任务的优先等级，分别提出了工作方式优先级加截止期(HPEDF)算法和截止期加工作方式优先级(EDHPF)算法。文献[13-14]进一步考虑了任务调度的及时性，提出了基于调度收益的算法。文献[15-16]通过引入目标威胁度，提出了基于动态优先级的调度算法。文献[17-18]提出了可变驻留时间的概念，并运用多重嵌套的启发式算法进行任务调度。启发式算法计算简便、复杂度低，但当问题的规模较大时，所求得的结果往往与最优解相差甚远。相比较而言，智能算法可以凭借其群体搜索、迭代进化等优势，求得更佳结果。文献[19-25]将改进的遗传算法应用于该问题中，增强了任务调度的稳健性和鲁棒性。虽然上述方法多样，但尚存在如下不足：1)部分算法[1-3，5-10，15-17,21-24]没有考虑任务的内部结构，限制了任务中等待期的利用；2)虽然部分文献[4，11-14，18-20]运用了交错调度技术，但没有构建任务调度的优化模型或仅构建了单一目标函数，难以保证算法在多方面的调度性能；3)大部分文献[1-18，21-24]仅采用单一算法进行求解，没有兼顾两类算法的优势。

因此，本文提出一种混合自适应遗传算法来求解相控阵雷达的任务调度问题。该算法运用交错调度技术，在多方面提供良好的调度性能的同时，可有效提升收敛速度。首先，以时间和能量为约束条件，综合任务调度的3大原则，建立相控阵雷达任务调度的最优化模型；其次，提出改进的自适应遗传算法并进行求解。在传统遗传算法的基础上，引入混沌理论优化初始种群，使种群初值具有良好的随机性和遍历性；采用精英保留和混合排名选择策略，以避免算法过早收敛于局部最优；设计了自适应交叉算子和变异算子，以提升算法的搜索效率。在智能算法的框架下，提出了启发式脉冲交错算法，以进一步提升时间的利用率。最后通过一系列仿真实验证明了该算法的有效性。

1 基本理论建模

1.1 雷达任务模型

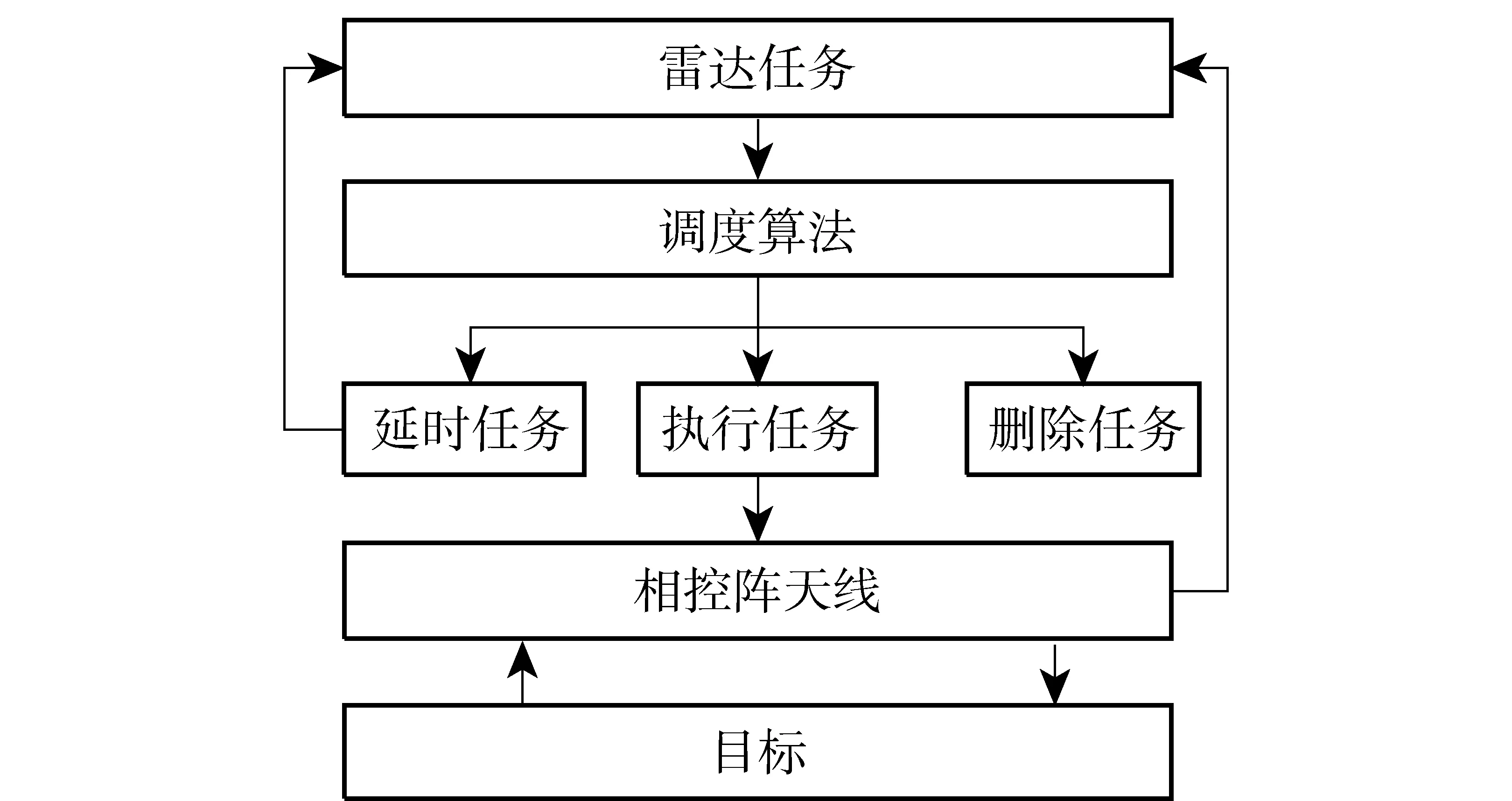
图1 相控阵雷达的任务调度框架Fig.1 Overall scheduling structure of phased array radar

图1为相控阵雷达的任务调度框架。由图1可知，当雷达捕获目标后，调度算法将根据任务的请求状态以及雷达的自身资源来调度任务。调度结果可分为执行队列、延时队列和删除队列。其中，延时队列中的任务将被再次送往请求队列，以期在后续的时间得到执行，执行队列和删除队列中的任务将分别被执行和删除。雷达任务的请求顺序一般为：搜索—确认—跟踪(—失跟处理—跟踪维持)。跟踪任务的种类可具体分为精跟、普跟和监视3种。图2给出了相控阵雷达的任务模型，从中可知，雷达任务主要由发射期、等待期和接收期3部分构成。第i个相控阵雷达任务[26-27]可以描述为

Ti={Pi,tai,txi,twi,tri,Pti,dwi,wi,tdi,Δti}，

(1)

式中：Pi为任务优先级；tai为任务请求执行时刻；txi为任务发射期持续时间；twi为等待期，长短由目标的距离决定；tri为接收期持续时间；Pti为任务执行完毕时消耗的功率；dwi为任务驻留时间；wi为任务时间窗；tdi为任务截止期；Δti为相邻两次任务之间的时间间隔。其中任务的驻留时间满足：

dwi=txi+twi+tri，

(2)

任务的截止期满足：

tdi=tai+wi，

(3)

相邻两次任务间请求时刻的关系为

tai=tei-1+Δti，

(4)

tei-1为上一次任务的成功执行时刻。

图2 相控阵雷达的任务模型Fig.2 Task model of phased array radar

1.2 资源约束模型

1.2.1 时间资源约束

调度间隔(SI)是相控阵雷达进行任务调度的基本单位。在一个SI内，雷达要处理前一个SI内的回波，并决定下一SI内的任务执行序列[26-27]。在一个SI内，成功执行的N1个任务在满足各自的截止期约束的同时，还需满足：

(5)

式中：SI为SI时长。由于任务在发射期和接收期内不能被中断，成功执行的N1个任务还需要满足：

(6)

(6)式表明，任务在发射期和接收期是不可抢占的，但等待期可以被有效利用。若任务不满足执行要求，则会被延时执行或被删除。

1.2.2 能量资源约束

(7)

式中：P(x)为雷达的功率函数；τ为回退参数，表示雷达的散热性能。

1.3 目标函数构建

雷达在调度任务过程中，应遵循以下几点原则：1)重要性原则，高优先级的任务应优先得到调度；2)紧急性原则，更加紧急的任务应优先得到调度；3)及时性原则，任务的实际执行时刻应尽可能接近其请求时刻[27]。因此，综合任务调度的三原则，构建(8)式所示的调度目标函数：

o(P,ta,w,ts,te)=
[o1(P)+o2(ta,w,ts)]o3(te,ta,w)，

(8)

式中：o1(P)为任务的重要性函数；o2(ta,w,ts)为任务的紧迫性函数；o3(te,ta,w)为任务执行的及时性函数；ts为SI开始时刻。(8)式构建的目标函数考虑了任务调度过程中的多项原则，从而保证了算法在多方面具有较佳的性能。

假设在一个SI内共有N个请求任务，经调度后执行、延时和删除队列中的任务个数分别为N1、N2和N3，则有N=N1+N2+N3. 因此相控阵雷达的任务调度优化模型[27]可表示为

(9)

式中：te为SI结束时刻；前4个条件为执行任务的约束，后2个条件分别对应延时和删除任务的约束。从中可以看出，相控阵雷达调度问题是NP难题，需要采取高效的算法对问题进行求解。

2 混沌自适应遗传算法

相比于其他智能算法而言，遗传算法具有无需先验知识和良好的全局寻优能力等优势，在非线性规划、约束求解等方面已经得到广泛应用[28]。但传统遗传算法的搜索效率低下，因此本文根据所设计的目标函数，采用改进的遗传算法对相控阵雷达任务调度问题进行求解。

2.1 混沌理论初始化

遗传算法模拟了自然界中生物的进化特性，种群通过不断地进行选择、交叉和变异操作完成优胜劣汰，从而找到目标函数的最优解。在运用遗传算法进行求解时，首先应对种群进行初始化。在传统遗传算法中，种群初始值是随机产生的，在求解过程中容易陷入局部极值。而混沌序列具有良好的随机性和遍历性等优点，可以作为避免算法在搜索过程中陷入局部极值的一种优化机制。因此，本文采用Logistic方程对种群进行混沌初始化：

λk+1=μλk(1-λk)，

(10)

式中：λk为混沌变量λ迭代k次后的结果，λ[0,1]；μ为混沌状态控制参数，μ[0,4]. 当μ=4且λ∉{0.25,0.50,0.75}时，产生的初始序列值将具有完全混沌特性[27，29]。

2.2 选择算子

选择操作、交叉操作和变异操作是遗传算法中的3个主要步骤。通过以上3个步骤，用新的优异个体(候选调度序列)替换较差的个体，可以完成种群的更新，促使算法找到最优解。在进行选择操作时，采用精英保留和混合排名相结合的策略：设算法中的种群规模为M，对种群中的个体按照适应值(在此为(8)式)由大到小进行排序后，选择前m个适应值最佳的个体直接遗传给下一代；其余的M-m个个体中第i个个体按照下式计算适应度：

(11)

然后，采用轮盘赌的方式确定父本。第i个个体被选择的概率可计算为

(12)

其中，精英保留策略是遗传算法收敛的重要条件；而采用上述混合排名选择策略，部分适应值较差的个体得以保留，从而保证了种群的多样性。

2.3 自适应交叉、变异算子

交叉和变异操作可以保证种群个体良好的遗传性和种群的多样性。其中：交叉操作是从两个被选择的父代中产生两个子代；变异操作是从一个被选择的父代中产生一个子代。交叉概率pc和变异概率pm在两项操作中起着重要作用：当概率较大时，算法的搜索速度较快，但容易过早收敛；当概率较小时，搜索出全局最优值的概率较大，但算法的搜索速度较慢。在此，本文提出一种根据适应值动态调整的交叉、变异概率调节公式：

(13)

(14)

式中：pc0和pc1为交叉概率的初始调节参数，决定了交叉概率的下界和上界，可以根据大量试验得出；f为个体适应值；fmax为当前种群中个体的最佳适应值；fmin为种群中个体的最差适应值；fa为种群中个体的平均适应值。(14)式中的各参数与(13)式相似。从(13)式和(14)式可以看出：当种群中个体的适应值低于种群的平均适应值时，个体将以较大的概率发生改变；当个体的适应值高于种群的平均适应值时，个体将以较大的概率得以保留。通过(13)式、(14)式可以使得算法的交叉、变异概率得以动态调整，从而提升算法的搜索效率。

2.4 启发式脉冲交错调度算法

如前所述，脉冲交错技术可以有效提升系统的时间利用率，但也使任务的调度分析更加复杂。图3所示为相控阵雷达任务交错执行的两种方式，从中可以看出，交错执行的两个任务需要满足(15)式所示的时间约束：

(15)

tw1≥tx2+tw2+tr2.

(16)

图3 相控阵雷达任务交错执行的两种方式Fig.3 Two ways of task interleaving of phased array radar

(15)式和(16)式分别对应图3(a)和图3(b). 同时，交错执行的任务还需要满足能量资源的约束。鉴于交错调度的复杂性，本文提出一种启发式任务交错调度分析方法如下：

在一个SI内，初始化剩余时间轴[ts,te]和功率指针Pt0. 若在该SI内存在N个请求任务，则算法中个体的基因个数为N. 其中每个基因代表了对应任务的候选执行时刻。对于每个个体的所有基因，按照FIFO原则排序后，分别记为任务1，2，3，…，N，对任务1的发射期进行时间资源约束分析：

(17)

若发射期不满足时间资源约束，则根据(9)式中的延时或删除条件将任务送入相应链表。若发射期满足时间资源约束，则更新剩余时间轴为[ts,te1]，[te1+tx1,te]，并继续分析任务1的接收期能否满足剩余时间资源约束：

(18)

若接收期不满足剩余时间资源约束，则根据 (9) 式中的延时或删除条件将任务送入相应链表，并重置剩余时间轴为[ts,te]. 若接收期满足剩余时间资源约束，则继续分析任务1能否满足(19)式的能量资源约束：

(19)

若任务1不能满足能量资源约束，则根据(9)式中的延时或删除条件将任务送入相应链表，并重置剩余时间轴为[ts,te]. 若任务1能够满足能量资源约束，则更新剩余时间轴为[ts,te1]，[te1+tx1,te1+tx1+tw1]，[te1+tx1+tw1+tr1,te]，并更新功率指针为

Pt0=Pt0e-tx1/τ+Pt1(1-e-tx1/τ).

(20)

然后，按照如上时间资源约束分析和能量资源约束分析方式，对剩余的N-1个任务进行可调度性分析，得到个体的执行任务序列、延时任务序列和删除任务序列，从而可以大大简化任务交错调度的复杂度、快速计算个体的适应值。

2.5 算法步骤

混合遗传算法的步骤可归纳如下：

步骤1参数初始化。确定初始种群的规模M，遗传代数G，混沌参数μ，精英保留数m，自适应交叉、变异算子的上下界pc0、pc1、pm0和pm1.

步骤2混沌初始化种群。采用实数编码方式对个体的基因进行编码，产生基因(任务的候选执行时刻)满足(9)式中的约束条件1的M个个体。个体的基因数量等于请求任务数量N，并根据(10)式对初始种群进行混沌优化。

步骤3适应值计算。通过(15)式～(20)式对个体的候选调度序列进行交错调度分析，根据个体对(9)式中约束条件的满足情况，计算个体的适应值((8)式)，并得到个体对应的执行、延时和删除队列。

步骤4选择操作。根据(11)式、(12)式，对种群采用精英保留和混合排名选择策略，得到父代个体。

步骤5自适应交叉操作。对每一个个体，产生一个(0,1)之间的随机数，并根据(13)式计算个体的交叉概率pc. 然后找出所有产生的随机数小于pc的个体，对第i个个体，选择与之不同的个体j进行交叉操作，产生(1,N)之间的随机数r，互换两个个体中位于第r个基因之后的所有基因，得到两个子代个体。

步骤6自适应变异操作。对于每一个个体中的所有基因，产生一个(0,1)之间的随机数，并根据(14)式计算个体的变异概率pm. 若随机数小于pm，则对该基因进行变异，产生一个与之前基因不同且满足(9)式中约束条件1的可行基因。在对所有基因进行检查后，得到子代个体。在经过交叉和变异操作后，子代个体必须不同于父代个体，且适应值需优于父代，否则产生的子代个体将被父代所替换。

步骤7若迭代次数达到遗传代数G上限，则算法结束，输出最优的调度序列；否则，转步骤3.

算法流程如图4所示。

3 仿真校验

3.1 评估指标

根据调度算法的设计原则，选取以下指标作为评判调度算法性能的标准：

图4 算法流程图Fig.4 Flow chart of algorithm

1)实现价值率(HVR)[9-13，27]，是指成功调度任务的优先级之和与请求调度任务的优先级之和的比值，用以反映算法是否满足重要性原则，如(21)式所示：

(21)

式中：Pi为任务的优先级，反映任务的重要程度；Ns和Ntot分别为调度成功的任务数量和请求任务数量。

2)调度成功率(SSR)[9-13，26-27]，是指成功调度的任务数量与请求调度的任务数量之比，用以反映调度算法是否满足紧急性原则，如(22)式所示：

SSR=Ns/Ntot.

(22)

3)时间利用率(TUR)[10-13，26-27]，是指成功执行所有任务的所用时间与可用时间Ttot的比值。在调度过程中，算法应充分利用可用时间资源来调度任务，如(23)式所示：

(23)

4)时间偏移率(ATSR)[10-11，27]，是指成功调度的任务执行时刻与其请求执行时刻的相对偏移程度，用以反映调度算法是否满足有效性原则，如(24)式所示：

(24)

(24)式表明，时间偏移率越低，算法的性能越佳。

3.2 参数设置

表1 雷达任务参数表

3.3 仿真结果及分析

图5和图6分别为4种算法的调度成功率和实现价值率对比曲线。从图5和图6可以看出：当目标数量小于20时，4种算法均能成功调度所有的请求任务，调度成功率和实现价值率均为1；当目标数量超过20时，启发式算法和AGA最先开始错失请求任务，调度成功率和实现价值率开始下降；当目标数量超过30时，HGA的调度成功率和实现价值率开始下降；当目标数量超过40时，本文改进算法的调度成功率和实现价值率开始下降；并且在开始错失请求任务后，相对于前3种算法，本文改进算法中的两条曲线下降更缓慢。在启发式算法和AGA中，雷达任务被视为非抢占式单个驻留，没有考虑任务的内部结构，限制了脉冲交错调度的运用，因此，启发式算法和AGA最先开始错失请求任务。而本文改进算法和HGA均运用了脉冲交错技术，使任务中的等待期得到充分利用，但相比较而言，本文改进算法取得的调度成功率和实现价值率更高。

图5 调度成功率对比Fig.5 Comparison of scheduling success ratios

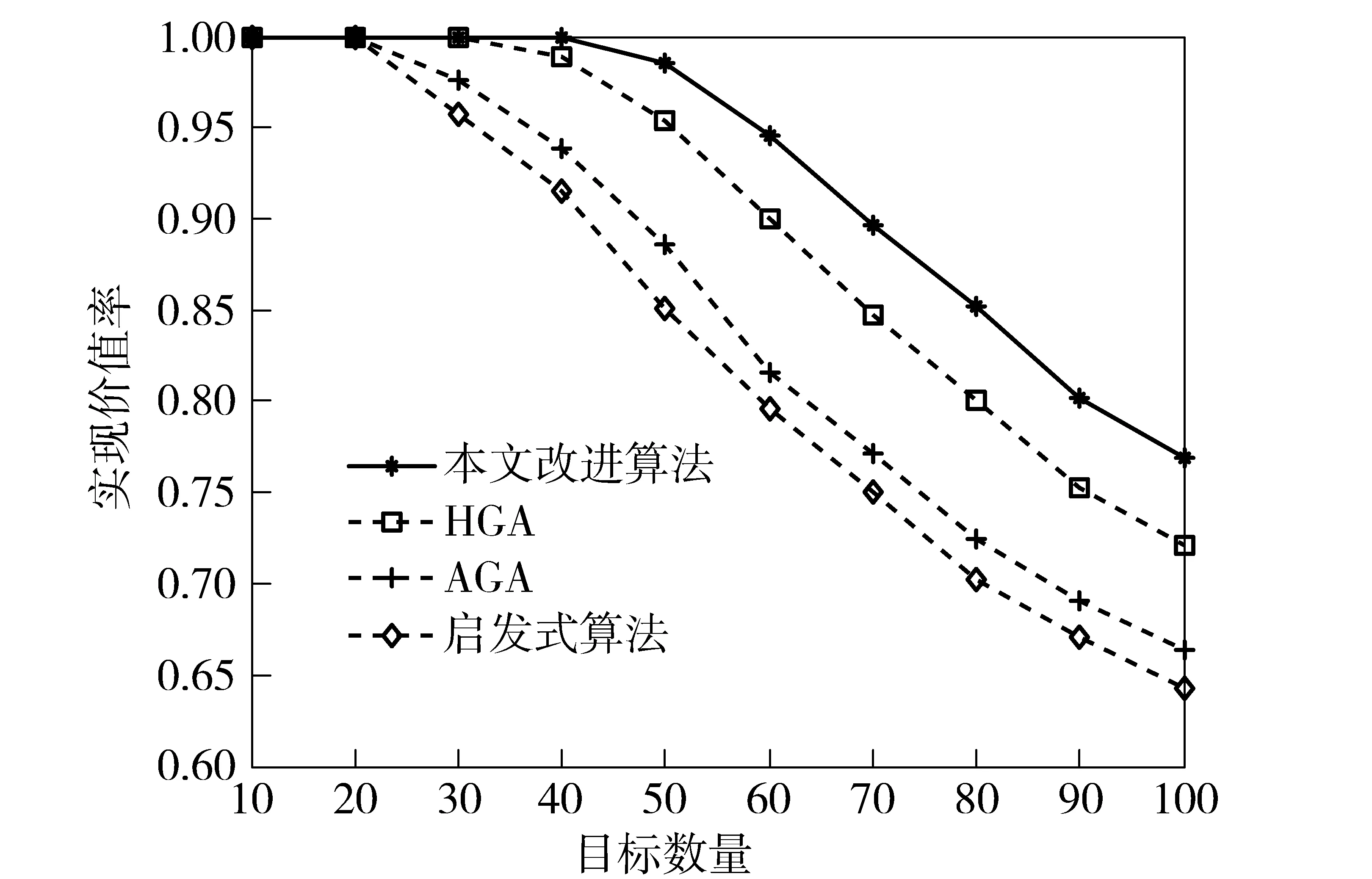
图6 实现价值率对比Fig.6 Comparison of high value ratios

图7为4种算法的时间利用率对比。从图7中可以看出，相对于启发式算法、AGA和HGA，本文改进算法取得了最高的时间利用率，更能够充分利用时间资源来调度请求任务。图8为4种算法的时间偏移率对比。图8中：本文改进算法和HGA的时间偏移率较低，控制在20%以内；启发式算法的时间偏移率较高，在45%～70%之间；AGA的时间偏移率居中。这主要是因为启发式算法通过预先设置的规则，优先对满足条件的任务进行调度，时间偏移率较高；本文改进算法和HGA利用种群优势可以进行全局搜索，因此取得的时间偏移率较低。相比于HGA，本文改进算法取得了更低的时间偏移率，表明改进算法能够更有效地执行搜索、跟踪等任务，以适应雷达工作环境的动态变化。虽然AGA同样采用了智能算法，但由于将雷达任务简化为非抢占式的单个驻留，调度柔性欠佳，相比于HGA和本文改进算法，时间偏移率略高。

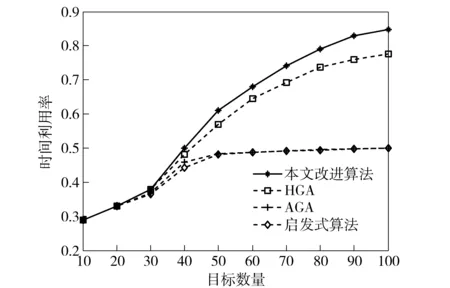
图7 时间利用率对比Fig.7 Comparison of time utilization ratios

图8 时间偏移率对比Fig.8 Comparison of average time shift ratios

图9(a)、图9(b)、图9(c)分别给出了目标数量为30、60和90时性能更佳的两种算法(本文改进算法和HGA)在单个SI内的平均收敛速度对比，以分别代表算法面临未过载、中度过载和严重过载任务量时的搜索性能。图9(a)的子图为HGA收敛速度的局部细节图，其横纵坐标与图9(a)～图9(c)一致。从图9中可以看出：HGA的初始种群质量不高、搜索效率较低，在迭代后期易产生阶跃现象，算法收敛速度较慢，容易陷入局部极值点；而本文改进算法的初始种群质量较高，收敛速度更快，寻优能力更佳。其原因可归纳为：

图9 本文改进算法和HGA的收敛速度对比Fig.9 Comparison of convergence rates of the improved algorithm and HGA algorithm

1) HGA采用启发式方法产生初始种群，初始种群质量较差；本文改进算法运用混沌理论，对初始种群进行了优化，使得初始种群分布遍历于整个解空间，提升了初始种群的质量。

2) HGA采用的适应值函数加惩罚函数方法本质上是最优选择策略，即适应值越大的个体被选择的概率越大，适应值越低的个体被选择的概率将更小，易使得算法仅对于适应值较优的个体邻域进行搜索，适应值差的个体邻域被忽略，算法过早陷入局部极值点。本文改进算法采用精英保留和混合排名相结合的选择策略，使得适应值大的个体得以保留，其他个体混合选择，适应值小的个体也有相同的机会被选择，保证了不同适应值的个体邻域均能被搜索，增强了算法的全局寻优概率。

3) HGA采用交换字串杂交、移动变异的策略，其概率均为恒定值。本文改进算法通过设计根据适应值动态调整的交叉、变异概率调节公式，使得交叉、变异概率可以根据个体的适应值进行调整：当种群中个体的适应值低于种群的平均适应值时，个体将以较大的概率发生改变；当个体的适应值高于种群的平均适应值时，个体将以较大的概率得以保留，提升了算法的搜索效率。

4)虽然HGA同样运用了交错调度算法，利用雷达任务的等待期来交错执行其他任务的发射期或接收期，以提升算法对于时间的利用率，但HGA考虑了能量约束，限制了交错执行的任务数量，同时将交错调度的约束条件迁移到染色体编码、交叉、变异操作中，使算法更加复杂。本文改进算法通过将能量约束公式化以及设计启发式的交错调度算法，在利用任务等待期的同时，无需考虑染色体进行交叉、变异时的约束，大大降低了算法的复杂度。

综上所述，本文改进算法中运用了混沌优化、精英保留和混合排名选择策略、自适应交叉、变异操作以及交错调度算法，因此搜索到了全局最优解；而HGA仅搜索到了次优解。相比于HGA，本文改进算法的收敛速度更快；相比于启发式算法，本文改进算法的调度成功率提升了40%，实现价值率提升了20%，时间利用率提升了70%，时间偏移率减少了80%.

4 结论

实现任务的优化分配是充分发挥相控阵雷达潜能的关键。本文提出了混合自适应遗传算法对该问题进行求解，所做的贡献和结论主要如下：

1)综合任务调度的重要性、紧急性和及时性原则，构建了相控阵雷达任务调度的优化模型。

2)利用混沌理论产生质量较高的初始种群；采用精英保留和混合排名的选择策略，在保证算法收敛性的同时赋予个体多样性；设计了自适应的交叉、变异算子，以提升算法的求解效率；提出了嵌套的启发式交错算法，以充分利用任务中的等待期。

3)仿真结果表明，相对于3种传统调度算法，本文提出的基于混合自适应遗传算法的调度算法性能更佳。相比于启发式算法，本文改进算法的调度成功率提升了40%，实现价值率提升了20%，时间利用率提升了70%，时间偏移率减少了80%.

下一步将综合更多的约束条件，对相控阵雷达的调度优化问题开展研究。

References)

[1] Zhang B Y, Li S H, Yan W, et al. An efficient scheduling method for phased array radars with limited time resources[C]∥Proceedings of the IET International Radar Conference. Guilin, China: IET, 2009: 1-4.

[2] Butler J M. Multi-function radar tracking and control[D]. London, UK: UCL University of London, 1998.

[3] Reinoso-Rondinel R, Yu T Y, Torres S. Multifunction phased-array radar: time balance scheduler for adaptive weather sensing[J]. Journal of Atmospheric and Oceanic Technology, 2010, 27(11): 1854-1867.

[4] Orman A J, Potts C N, Shahani A K, et al. Scheduling for a multi-function phased array radar system[J]. European Journal of Operational Research, 1996,90(1): 13-25.

[5] 曾光, 胡卫东, 卢建斌, 等. 多功能相控阵雷达自适应调度仿真[J]. 系统仿真学报, 2004, 16(9): 2026-2029. ZENG Guang, HU Wei-dong, LU Jian-bin, et al. The simulation on adaptive scheduling for multifunction phased array radars[J]. Journal of System Simulation, 2004, 16(9): 2026-2029.(in Chinese)

[6] Bolderheij F, Absil F G J, van Genderen P. A risk-based object oriented approach to sensor management[C]∥Proceedings of the 7th International Conference on Information Fusion. Philadelphia, PA, US: IEEE, 2005: 1-8.

[7] Jimenez M I, del Val L, Villacorta J J. Design of task scheduling process for a multifunction radar[J]. IET Radar, Sonar and Navigation, 2012, 6(5): 341-347.

[8] 卢建斌, 胡卫东, 郁文贤. 相控阵雷达实时任务调度研究[J]. 电子学报, 2006, 34(4): 732-736. LU Jian-bin, HU Wei-dong, YU Wen-xian. Research on real-time scheduling algorithm for multifunction phased array radar[J]. Acta Electronica Sinica, 2006, 34(4): 732-736. (in Chinese)

[9] Lu J B, Xiao H, Xi Z M, et al. Multifunction phased array radar resource management: real-time scheduling algorithm[J]. Journal of Computational Information Systems, 2011, 7(2): 385-393.

[10] Lu J B, Xiao H, Xi Z M, et al. Phased array radar resource management: task scheduling and performance evaluation[J]. Journal of Computational Information Systems, 2013, 9(3): 1131-1138.

[11] Cheng T, He Z S, Tang T. Novel radar dwell scheduling algorithm based on pulse interleaving[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 247-253.

[12] Cheng T, He Z S, Li H Y. Adaptive dwell scheduling for digital array radar based on online pulse interleaving[J]. Chinese Journal of Electronics, 2009, 18(3):574-578.

[13] Cheng T, He Z S, Tang T. Dwell scheduling algorithm for multifunction phased array radars based on the scheduling gain[J]. Journal of Systems Engineering and Electronics, 2008, 19(3):479-485.

[14] Chen J, Tian Z, Wang L, et al. Adaptive simultaneous multi-beam dwell scheduling algorithm for multifunction phased array radars[J]. Journal of Information and Computational Science, 2011, 8(14): 3051-3061.

[15] 张浩为, 谢军伟, 师俊朋, 等. 饱和时序下防空相控阵雷达动态优先级调度算法[J]. 北京航空航天大学学报, 2016, 42(12): 2722-2729. ZHANG Hao-wei, XIE Jun-wei, SHI Jun-peng, et al. Dynamic priority scheduling algorithm for air defense phased array radar in overload situations[J]. Journal of Beijing University Aeronautics and Astronautics, 2016, 42(12): 2722-2729.(in Chinese)

[16] 张浩为, 谢军伟, 盛川. 综合优先级规划下的相控阵雷达自适应调度方法[J]. 兵工学报, 2016, 37(11): 2164-2169. ZHANG Hao-wei, XIE Jun-wei, SHENG Chuan. Adaptive scheduling algorithm over comprehensive priority for phased array radar[J]. Acta Armamentarii, 2016, 37(11): 2164-2169.(in Chinese)

[17] Mir H S, Abdelaziz F B. Cyclic task Sscheduling for multifunction radar[J]. IEEE Transactions on Automation Science and Engineering, 2012, 9(3): 529-537.

[18] Mir H S, Guitouni A. Variable dwell time task scheduling for multifunction radar[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 463-472.

[19] 周颖, 王雪松,汪连栋,等.基于遗传算法的相控阵雷达最优化调度研究[J]. 系统工程与电子技术, 2005, 27(12): 1977-1980. ZHOU Ying, WANG Xue-song, WANG Lian-dong, et al. Optimal scheduling for phased array radar based on genetic algorithm[J]. Systems Engineering and Electronics, 2005, 27(12): 1977-1980.(in Chinese)

[20] 周颖, 王国玉, 王雪松, 等. 基于启发式混合遗传算法的相控阵雷达最优化调度[J]. 系统工程与电子技术, 2006, 28(7): 992-996. ZHOU Ying, WANG Guo-yu,WANG Xue-song, et al. Optimal scheduling using hybrid GA with heuristic rules for phased array radar[J]. Systems Engineering and Electronics, 2006, 28(7): 992-996.(in Chinese)

[21] Wang S J, He J, Wang B, et al. Research on adaptive scheduling algorithm based on improved genetic algorithm for multifunctional phased array radar[C]∥Proceedings of International Conference on Future Computer and Communication Engineering. Tianjin:Atlantis Press, 2014:13-20.

[22] 潘伟. 自适应遗传算法在相控阵雷达最优化调度中的应用[J]. 电子信息对抗技术, 2014, 29(1): 38-41. PAN Wei. Application of adaptive genetic algorithm to optimal scheduling of phased array radar[J]. Electronic Information Warfare Technology, 2014, 29(1): 38-41.(in Chinese)

[23] 王帅杰, 何俊, 王斌, 等. 改进遗传算法的相控阵雷达自适应调度算法及仿真[J]. 火力与指挥控制, 2015, 40(9): 88-91. WANG Shuai-jie, HE Jun, WANG Bin, et al. Adaptive scheduling algorithm based on improved genetic algorithm for multifunctional phased array radar[J]. Fire Control & Command Control, 2015, 40(9): 88-91. (in Chinese)

[24] 郑玉军, 田康生, 邢晓楠, 等. 基于小生境遗传算法的相控阵雷达任务调度[J]. 现代防御技术, 2016, 44(1):168-174. ZHENG Yu-jun, TIAN Kang-sheng, XING Xiao-nan, et al. Optimal scheduling for phased array radar based on niche genetic algorithm[J]. Modern Defence Technology, 2016, 44(1):168-174. (in Chinese)

[25] Zhang H W, Xie J W, Sheng C. Scheduling method for the phased array radar over chaos adaptively genetic algorithm[C]∥Proceedings of the 6th International Conference on Information Science and Technology. Dalian: IEEE, 2016:111-116.

[26] 张浩为, 谢军伟, 师俊朋, 等. 动态优先级下防空相控阵雷达在线交错调度算法[J]. 系统工程与电子技术, 2017, 39(3): 1-7. ZHANG Hao-wei, XIE Jun-wei, SHI Jun-peng, et al. Dynamic priority online interleaving scheduling algorithm for the air defense phased array radar[J]. Systems Engineering and Electro-nics, 2017, 39(3): 1-7. (in Chinese)

[27] 张浩为, 谢军伟, 张昭建, 等. 基于混合遗传- 粒子群算法的相控阵雷达调度方法[J]. 系统工程与电子技术，2017，39(9)：1985-1991. ZHANG Hao-wei, XIE Jun-wei, ZHANG Zhao-jian, et al. Scheduling based on the hybrid genetic particle swarm algorithm for the phased array radar[J].Systems Engineering and Electronics, 2017,39(9):1985-1991. (in Chinese)

[28] 张献, 任耀峰, 王润芃. 基于自适应遗传算法的连续时空最优搜索路径规划研究[J]. 兵工学报, 2015, 36(12): 2386-2395. ZHANG Xian, REN Yao-feng, WANG Run-peng. Research on optimal search path programming in continuous time and space based on an adaptive genetic algorithm[J]. Acta Armamentarii, 2015, 36(12): 2386-2395. (in Chinese)

[29] 刘爱军, 杨育, 李斐, 等. 混沌模拟退火粒子群优化算法研究及应用[J]. 浙江大学学报:工学版, 2013, 47(10): 1723-1730. LIU Ai-jun, YANG Yu, LI Fei, et al. Chaotic simulated annealing particle swarm optimization algorithm research and its application[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(10): 1723-1730. (in Chinese)

[30] Kuo T W, Chao Y S, Kuo C F, et al. Real-time dwell scheduling of component-oriented phased array radars[J]. IEEE Transactions on Computers, 2005, 54(1)： 47-60.

TaskSchedulingofPhasedArrayRadarBasedonHybridAdaptiveGeneticAlgorithm

ZHANG Hao-wei1, XIE Jun-wei1, ZHANG Zhao-jian1, ZONG Bin-feng2, CHEN Tang-jun3

(1.Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, Shaanxi, China；2.Unit 94710 of PLA, Wuxi 214000, Jiangsu, China；3.Unit 94921 of PLA, Jinjiang 362200, Fujian, China)

TN954+.2

A

1000-1093(2017)09-1761-10

10.3969/j.issn.1000-1093.2017.09.013

2017-01-03

国家自然科学基金青年科学基金项目(61503408)

张浩为 (1992—), 男, 博士研究生。E-mail: zhw_xhzf@163.com

谢军伟(1970—)，男，教授，博士生导师。E-mail: xjw_xjw_123@163.com