J-lay铺管作业力学分析
2017-10-11刘大辉阮伟东
刘大辉,阮伟东,白 勇
(浙江大学 建筑工程学院,浙江 杭州 310058)
J-lay铺管作业力学分析
刘大辉,阮伟东,白 勇
(浙江大学 建筑工程学院,浙江 杭州 310058)
目前J-lay铺管法作为深水和超深水铺管的最适用方法广泛应用于深海油气开发。考虑J-lay铺管时管道几何非线性特征以及触地区边界效应,将J-lay铺管模型划分三构件进行力学分析:悬浮段、边界层段以及触地段。建立OrcaFlex模型和引入Wang改进二构件模型,通过对比上述三种方法计算J-lay相应构型、轴力、弯矩和剪力分布,验证该三构件模型的可行性和考虑边界效应的必要性。基于Lamé公式计算管道横截面处轴向、径向以及环向应力,对比分析J-lay铺设管道应力分布特征。结果表明:该改进三构件模型能真实有效地模拟J-lay铺管过程中管道受力情况,特别是触地点附近弯矩和剪力变化情况,能为管道疲劳损伤分析提供理论基础。
J-lay铺管;三构件模型;边界效应;弯矩失真;剪力连续
Abstract: Nowadays J-lay pipelaying method, as the most suitable pipelaying method in deepwater and ultra-deepwater, has been widely used in the deepwater oil and gas development. By taking account of pipeline geometrical nonlinearity and boundary effect in the touchdown zone during J-lay pipelaying operation, J-lay pipelaying model is divided into three segments to study: suspended segment, boundary-layer segment and touchdown segment. J-lay FEM is developed by OrcaFlex software and the developed two-fields model proposed by Wang is also introduced. By comparing the results of the J-lay configuration, tension, bending moment and shear distributions obtained from the three methods above, it can strongly demonstrate the feasibility of the proposed three-fields model and the necessity of considering the boundary effect. Based on Lamé’s equations, the axial, radial and hoop stresses on pipe cross section can be obtained and the corresponding stress distribution characteristics can also be derived. The results show that: the proposed three-fields model can realistically and effectively simulate the pipeline loading performance in J-lay pipelaying operation, especially for the variation of the bending moment and shear force near the touchdown point. It will provide a theoretical basis for pipeline fatigue damage analysis.
Keywords: J-lay pipelaying; three-fields model; boundary effect; moment distortion; shear continuity
如图1所示,J-lay铺管由于铺管过程中管线形态呈“J”型而得名[1]。J-lay铺管采用近乎垂直形态进行铺管作业,有效减小悬浮段长度,从而降低铺管船的水平动力需求,同时缩短管道触地点与铺管船距离便于动力定位[2]。目前J-lay铺管已广泛应用于深海铺管作业,特别是墨西哥湾海域。而国内外关于J-lay铺管力学研究主要包括两方面:软件模拟和理论求解。其中软件模拟主要采用Abaqus和OrcaFlex等对J-lay铺管进行静态参数分析[3]和动态响应研究[4-6]。而理论研究主要包括:Lenci等[7]针对J-lay铺管建立四种力学分析模型,指出不能忽略触地点附近边界效应,否则将会导致弯矩失真和剪力不连续。Wang等[8]在Lenci提出的二构件模型基础上,充分考虑土体埋深和海流作用建立J-lay铺管力学模型,同时在三构件模型基础上考虑塑性海床作用,对比分析弹塑性海床作用下J-lay铺管不同响应[9]。白勇等[10-11]将柔性管材料非线性特性引入二构件模型,研究Reel-lay铺管作业柔性管力学特征。上述理论研究没有同时考虑水动力荷载和触地点附近边界效应,基于三构件模型引入Morison方程计算海流水动力荷载,通过控制触地点和边界层点的连续条件,采用打靶法计算J-lay铺管受力情况。同时对比OrcaFlex模型和Wang[8]改进二构件模型,验证该改进三构件模型的可行性和精确性,基于Lamé公式进行管道横截面应力分析,为立管触地点附近疲劳分析提供理论基础。
1 理论假定
由于海床抗力和水动力荷载作用,在实际工程中J-lay铺管作业力学分析比较复杂。为了便于进行J-lay铺管模型力学分析,作出以下假设:
1) 该理论模型为平面内静态分析,即管道运动和海流作用于同一平面内;
2) 不考虑管道的轴向变形和剪切变形;
3) 海床简化为线弹性水平海床。

图1 J-lay铺管安装Fig. 1 J-lay pipe laying
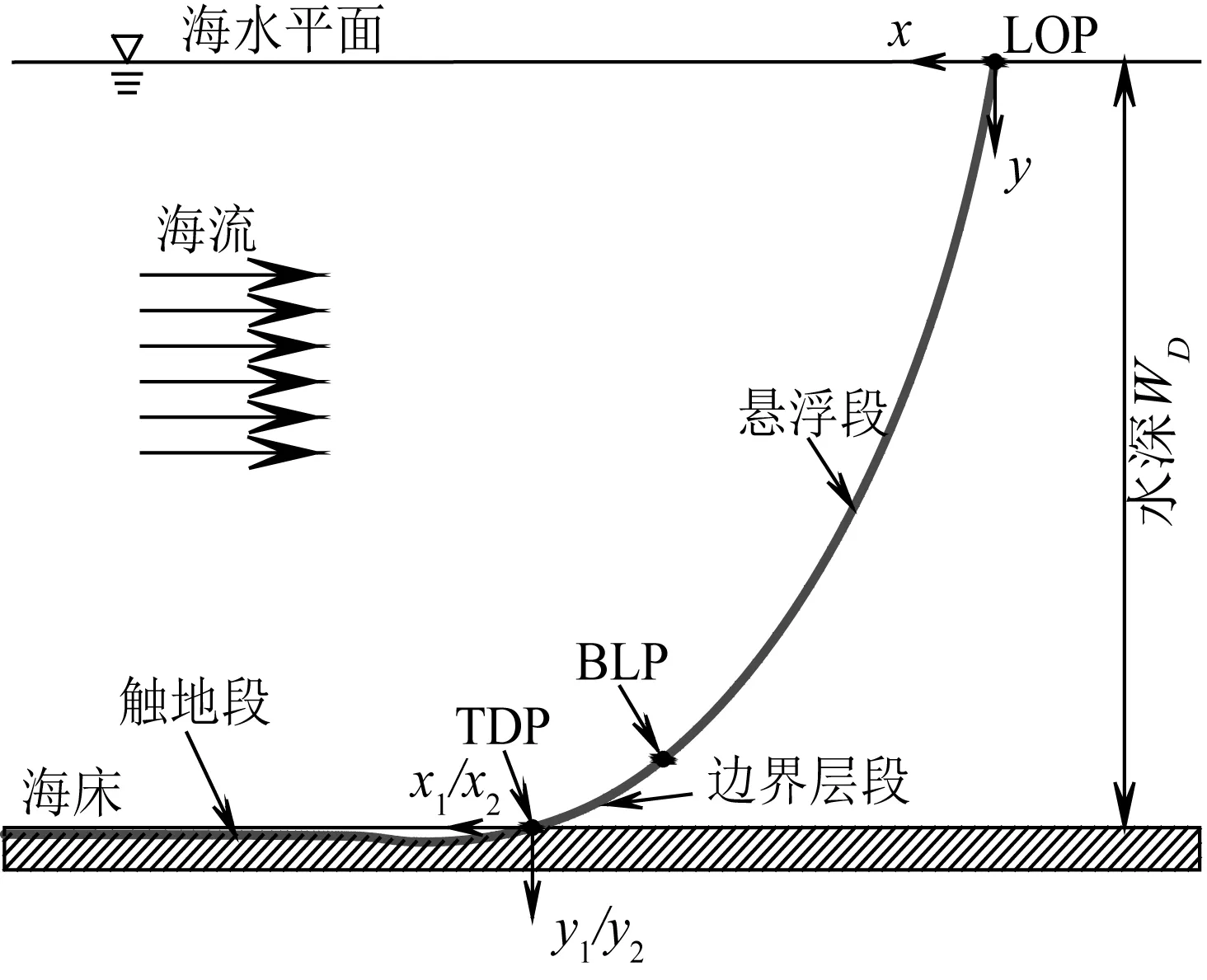
图2 J-lay铺管模型示意Fig. 2 Schematic diagram of J-lay model
2 J-lay铺管力学模型
以管道中心线描述管道运动,基于Ruan等[12]关于缓波构型理论研究,该J-lay铺管模型分为三部分构件进行力学分析(如图2所示):
1) 悬浮段:从顶部脱离点( LOP)到边界层点( BLP)之间的管段,由于深水作业中悬浮段很长,故忽略悬浮段抗弯刚度;
2) 边界层段:从边界层点( BLP) 到触地点( TDP) 之间的管段,由于边界层段非常接近海床并存在边界效应,因此将它单独作为一构件进行力学分析;

图3 悬浮段微分单元受力示意Fig. 3 Force sketch of a differential element of the suspended segment
3) 触地段:触地点( TDP) 之后置于海床上的管段。
如图2所示,在J-lay模型中分别建立三个坐标系统:整体坐标系(x,y)原点位于顶部脱离点( LOP),用于描述J-lay整体构型特征;局部坐标系(x1,y1)和(x2,y2)原点都位于触地点(TDP),分别用于描述边界层段和触地段构型特征。
2.1悬浮段
管道自脱离点(LOP)从铺管船分离铺设下放,主要承受顶部张力和水动力荷载。顶部张力如果过大将会导致管端脱离点处应力过大而强度失效。
如图3所示,将悬浮段划分成若干微分单元进行力学分析,通过微分单元受力平衡计算得到:


式中:T,H和V分别为节点轴力、水平力和竖直力;dH,dV和dM分别为水平力、竖直力和弯矩增量;Fn和Fτ分别为单位长度法向和切向拖曳力,Cd和Cτ为相应拖曳力系数;ρw为海水密度;vc为海流速度;Do为管道外径;we为管道单位长度有效湿重,we=w+ρigAi-ρwgAo;w为管道单位长度重量;ρi为内流密度;Ao为管道外截面面积,Ai为管道内截面面积;g为重力加速度;ds为微分单元长度;θ为管道倾角。
管道抗弯刚度将会导致式(3)极难求解,因此将悬浮段简化为悬链线构件。基于忽略悬浮段抗弯刚度假定,管道倾角θ可以通过式(3)近似计算:
管道曲率κ可以通过下式计算:
由于不考虑管道轴向变形和剪切变形,微分单元的水平和竖直增量表达式为:
一旦计算得到悬浮段构型、倾角以及曲率,管道近似弯矩和剪力可以采用以下公式计算:
式中:EI为管道抗弯刚度,弯矩以底部受拉为正,剪力以顺时针方向为正。
2.2边界层段
许多学者一般忽略边界层段抗弯刚度进行铺管力学分析,这将导致触地点附近弯矩失真以及剪力不连续。由于局部屈曲和压缩变形失效主要发生在触地点附近,因此考虑触地点附近边界效应对J-lay铺管模型分析具有极其重要意义。
图4为边界层段的微分单元力学分析模型。从图中可以看出该模型没有考虑边界层段受到的海流作用。由于边界层段非常接近海床,其倾角非常小,因此适用欧拉-伯努利梁理论。此外,为了便于进行力学分析理论假定边界层段受到的轴力为定值,其力学模型可表示为:
式中:T为边界层段恒定轴力,L为BLP在局部坐标系(x1,y1)中的x1坐标。方程(12)为四阶常微分方程,其通解为:

其中,c1、c2、c3和c4为未知量。
基于欧拉-伯努利梁理论,边界层段弯矩和剪力可以通过以下公式计算:
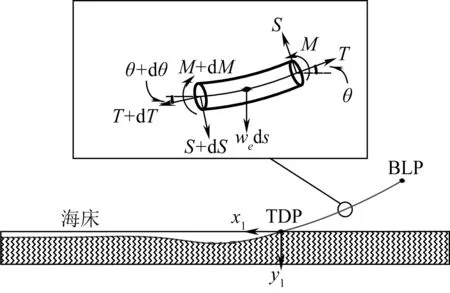
图4 边界层段微分单元受力示意Fig. 4 Force sketch of a differential element of the boundary-layer segment

图5 触地段微分单元受力示意Fig. 5 Force sketch of a differential element of the touchdown segment
2.3触地段
如图5所示,触地段主要受到管道有效湿重、海床抗力以及触地点处张力。管道通过陷入一定海床深度以达到有效重力和海床抗力平衡,进而抑制管道侧向运动,避免管道海底失稳和侧向屈曲。
由于需要综合考虑海床土体特性、复杂外界环境、管道几何形状,很难完全真实地模拟管道和海床的相互作用[13]。目前管土相互作用理论模型主要采用节点弹簧约束模型,从线性弹簧刚度模型发展到非线性弹簧刚度模型,最后发展到考虑海床土壤刚度衰减的弹簧刚度模型[14]。此外,国内外一般采用模型试验和数值模拟研究管土相互作用机理[15-16]。本文理论模型采用线弹性弹簧刚度模型模拟海床抗力,从而计算触地段埋深。基于欧拉-伯努利梁理论,触地段竖直平衡控制方程可表达为:
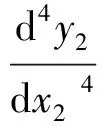


其中,c5、c6、c7和c8为未知数,
当x2→∞,海床受到竖直抗力等于管道有效湿重,即y2=we/k。因此,c7和c8都等于0,式(18)可以简化为:

触地段弯矩和剪力计算方法与边界层段相同。
2.4边界条件
J-lay铺管在脱离点(LOP)处边界条件为:
其中,θ0为脱离点管道倾角。
2.5管道应力
管道横截面处应力变化对疲劳损伤计算至关重要。如图6所示,横截面最大轴向应力为直接拉伸应力和弯曲应力的总和(即σt=σa±σm)。而直接拉伸应力σa和弯曲应力σm分别可以通过壁厚轴力和弯矩计算得到:
其中,Tw为壁厚轴力,Te为有效轴力,I为管道横截面惯性矩。考虑内外压以及轴向荷载作用于厚壁管道,管道径向应力σr和环向应力σθ可以通过Lamé公式计算得到:

其中,a=(po-pi)ro2ri2/(ro2-ri2),b=(piAi-poAo)/At,pi和po分别为管道内外压,ri和ro分别为管道内外半径,At为管道横截面面积。

图6 管道横截面轴向应力分布Fig. 6 Axial stress distribution acting on a pipe cross section
3 数值方法
在该数值分析中,脱离点轴力T0和边界层点倾角θBLP为未知量。一旦求得T0和θBLP值,便可通过式(24)-(31)采用递推法从LOP计算得到悬浮段构型和受力情况,同时计算出悬浮段长度。

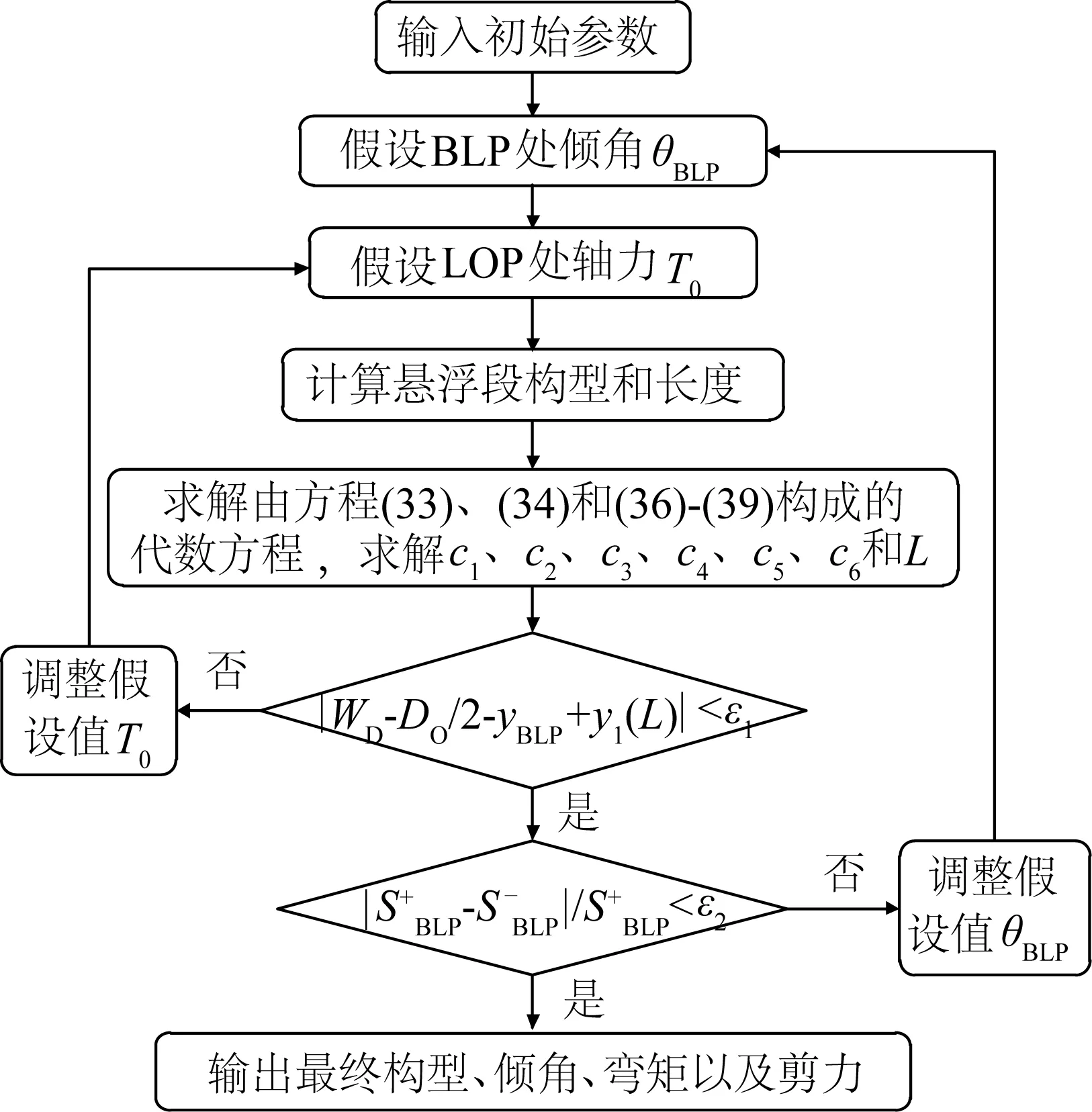
图7 数值计算流程Fig. 7 Flow chart of numerical calculation
该改进三构件模型必须确保BLP和TDP处位移、倾角、曲率(弯矩)以及剪力连续:式(32)-(35)为BLP处连续条件,式(36)-(39)为TDP处连续条件。考虑管道直径效应,方程(32)中真实水深WD需要减掉管道半径Do/2。
J-lay模型计算流程可以归纳为以下步骤:首先,提前假设T0和θBLP值,其中T0可以悬链线理论近似求解;通过式(24)-(31)计算悬浮段构型,因此相应位移、倾角、曲率、剪力以及轴力为包含T0和θBLP隐函数;之后,考虑BLP和TDP处位移、倾角、曲率(弯矩)以及剪力连续,式(32)-(39)包含7个未知数c1、c2、c3、c4、c5、c6和L,上述7个未知数可以通过式(33)、(34) 和(36)-(39)求解得到;可以发现还剩余两个方程(32)和(35),由于T0和θBLP值为假设值,并非真实值,因此T0和θBLP可以通过式(32)和(35)求解得到;最后,一旦上述9个未知数全部求解得到,可以计算得到J-lay铺管整体构型。图7为该力学模型数值计算流程图,其中ε1和ε2为极小值。
4 结果分析
通过OrcaFlex有限元建模以及Wang[8]改进二构件模型引入,验证分析改进三构件理论模型的可行性和精确性。其中,OrcaFlex有限元模型采用线弹性海床模型,该线性海床模型Normal stiffness=k/Do。表1为管道基本参数,表2为环境参数以及其他参数。表3为改进三构件理论模型、Wang[8]改进二构件模型以及OrcaFlex模拟计算结果对比。

表1 管道参数Tab. 1 Pipeline parameters
注:Di为管道内径,EA为管道拉伸刚度。

表2 环境和其他参数Tab. 2 Environmental and other parameters
图8分别为上述三种方法J-lay构型、有效轴力、弯矩和剪力整体对比图,以及为触地点附近构型、有效轴力、弯矩和剪力局部对比图。


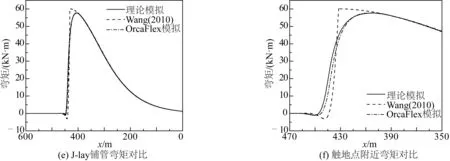

图8 三种方法J-lay构型、有效轴力、弯矩和剪力整体及局部对比Fig. 8 Comparison of J-lay configurations, effective tensions, bending moments and shear forces
从图8(a)~8(d)可以看出J-lay构型和有效轴力三种方法吻合比较好,主要区别发生在触地点附近。通过改进三构件理论模型、改进二构件模型和OrcaFlex模拟计算得到的触地点x坐标分别为438.58 m、431.43 m和436.63 m,可见是否考虑触地点附近边界效应对J-lay铺管构型基本没有影响。但是,从图8(d)可以发现改进三构件理论模型在触地点附近的有效轴力与改进二构件模型和OrcaFlex模拟计算结果有明显偏差。这是由于该理论模型假定边界层段和触地段的有效轴力保持定值,所以改进三构件理论模型计算边界层段和触地段的有效轴力曲线呈水平线,略大于另外两种方法计算值。
如图8(e)、(f)所示,Wang改进二构件模型求解的弯矩曲线在触地点处并不光滑,最大正弯矩和最小负弯矩绝对值都大于改进三构件理论模型和OrcaFlex模拟计算结果,其中Wang改进二构件模型与OrcaFlex模拟计算最大正弯矩误差大约为4.2%。而从图8(f)可以发现改进三构件理论模型和OrcaFlex模拟的弯矩曲线非常接近。由于J-lay铺管触地点附近的轴向应力主要由弯矩荷载控制,从而进行触地点附近疲劳损伤评估,因此这充分体现改进三构件模型考虑触地点附近边界效应的优势。
如图8(g)、(h)所示,改进三构件理论模型和OrcaFlex模拟的剪力曲线在触地点附近非常接近,其最大剪力分别为4.46 kN和4.54 kN。而Wang改进二构件模型计算的剪力曲线在触地点附近与另外两种方法有显著区别,最大剪力为13.06 kN,远远大于真实最大剪力值。这是由于Wang改进二构件模型没有考虑触地点附近边界效应,只保证弯矩在触地点处的连续,没有考虑剪力连续,因此该方法计算得到的剪力在触地点发生突变,从侧面说明触地点附近弯矩失真。
从图8可以发现最大有效轴力发生在顶端脱离点处,最大弯矩和最大剪力主要发生在触地点附近。根据Lamé公式可以计算管道横截面处最大轴向、径向以及环向应力沿x坐标分布(图9)。由于管道轴向应力主要由弯矩荷载控制,如图9(a),最大轴向应力发生在立管触地点附近。此外可以发现Wang改进二构件模型计算触地点附近最大轴向应力要略大于其它两种方法,这是由于Wang改进二构件模型在触地点附近最大弯矩荷载要大于其他两种方法。由于该算例中海水密度要稍大于内流密度,管道横截面受到的径向和环向应力都处于压缩状态,都随着水深的增加而不断增加。通过对比上述三种应力,可以发现触地点附近轴向应力要远大于径向和环向应力,同时触地点附近是深海J-lay铺管管道应力响应最大位置。由此可见,轴向应力的精确预测对疲劳分析非常重要。

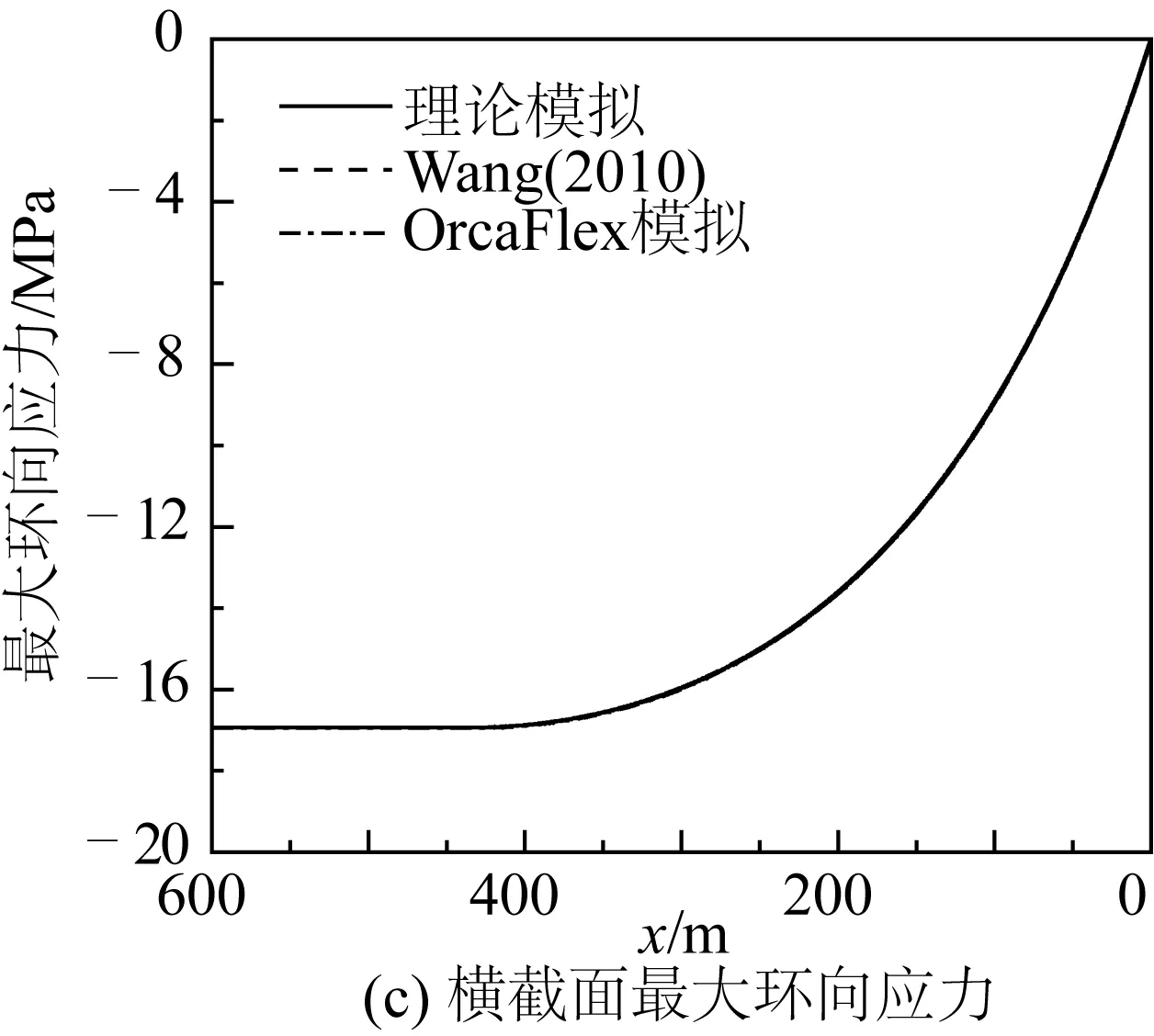
图9 横截面最大轴向应力、最大径向应力和最大环向应力对比Fig. 9 Comparison of maximum axial stresses, maximum radial stresses and maximum hoop stresses

项目T0/kNTTDP/kNMmax/(kN·m)xTDP/memax/mmSmax/kNσt,max/MPaσr,max/MPaσθ,max/MPa理论模型1068.11155.2457.68438.5814.504.46125.46-10.04-16.94Wang(2010)1068.62151.2660.14431.4324.8613.06130.35-10.04-16.94OrcaFlex模拟1068.63150.8357.73436.6314.624.54125.32-10.05-16.95误差/(%)0.052.920.090.450.821.760.110.100.06
注:TTDP为TDP处有效轴力,Mmax为管道最大弯矩,xTDP为TDP处x坐标,emax为管道最大海床陷深,Smax为最大剪力,σt,max为最大轴向应力,σr,max为最大径向应力,σθ,max为最大环向应力,误差为理论方法和OrcaFlex模拟结果的相对误差分析。
5 结 语
1) 该J-lay力学模型通过引入海流作用改进三构件模型,建立OrcaFlex模型和引入Wang改进二构件模型,对比分析上述三种方法求解的J-lay铺管构型、有效轴力、弯矩以及剪力等情况,有效验证改进三构件模型的可行性和精确性。
2) 对J-lay铺管作业进行力学分析时,必须考虑触地点附近的边界效应,否则将会导致该区域弯矩失真以及剪力突变。
3) J-lay铺管管道最大有效轴力发生在顶端脱离点处,最大弯矩和最大剪力主要发生在触地点附近。由于管道轴向应力主要由弯矩荷载控制,最大轴向应力发生在立管触地点附近。
4) 当海水密度要稍大于内流密度时,管道横截面受到的径向和环向应力都处于压缩状态,都随着水深的增加而不断增加。
5) 触地点附近轴向应力要远大于径向和环向应力,同时触地点附近是深海J-lay铺管管道应力响应最大位置。由此可见,轴向应力的精确预测对管道疲劳损伤分析非常重要。
[1] BAI Q, BAI Y. Subsea pipeline design, analysis, and installation[M]. Gulf Professional Publishing, 2014.
[2] 何宁, 徐崇崴, 段梦兰, 等. J 型铺管法研究进展[J]. 石油矿场机械, 2011, 40(3): 63-67. (HE Ning, XU Chongwei, DUAN Menglan, et al. Overview of J-lay technology for subsea pipelines[J]. Oil Field Equipment, 2011, 40(3): 63-67. (in Chinese))
[3] 陈景皓, 段梦兰, 徐崇崴, 等. 深水海底管道 J 形铺设参数[J]. 油气储运, 2013, 32(6): 654-658. (CHEN Jinghao, DUAN Menglan, XU Chongwei, et al. Parameters of J-lay method for deepwater submarine pipeline[J]. Oil & Gas Storage and Transportation, 2013, 32(6): 654-658. (in Chinese))
[4] 沙勇, 周巍伟, 李丽玮, 等. 深水海底管道 J 型铺设的动态分析[J]. 工程力学, 2014, 31(增刊): 228-230,238. (SHA Yong, ZHOU Weiwei, LI Liwei, et al. The dynamic analysis of a depwater pipeline installed by J-lay method[J]. Engineering Mechanics, 2014, 31(S): 228-230,238. (in Chinese))
[5] 王知谦, 杨和振. 深海 J 型铺管法管线触地区域动力响应研究[J]. 海洋技术学报, 2014, 33(5): 101-106. (WANG Zhiqian, YANG Hezhen. Study on touch down zone dynamics of pipelines during deep sea J-lay installation[J]. Journal of Ocean Technology, 2014, 33(5): 101-106. (in Chinese))
[6] 叶茂, 段梦兰, 徐崇崴, 等. J 形铺设过程管道动态分析与研究[J]. 石油机械, 2013 (6): 43-48. (YE Mao, DUAN Menglan, XU Chongwei, et al. Dynamic analysis and study of J-shaped pipeline-laying process[J]. China Petroleum Machinery, 2013 (6): 43-48. (in Chinese))
[7] LENCI S, CALLEGARI M. Simple analytical models for the J-lay problem[J]. Acta Mechanica, 2005, 178(1-2): 23-39.
[8] WANG L Z, YUAN F, GUO Z, et al. Numerical analysis of pipeline in J-lay problem[J]. Journal of Zhejiang University, Science A, 2010, 11(11): 908-920.
[9] WANG L Z, YUAN F, GUO Z, et al. Analytical prediction of pipeline behaviors in J-lay on plastic seabed[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011, 138(2): 77-85.
[10] BAI Y, YU B, CHENG P. Offshore installation of reinforced thermoplastic pipe (RTP)[C]//Proceedings of the Twenty-second International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2012.
[11] 白勇, 唐继蔚, 余彬彬, 等. 柔性管 Reel-lay 铺管安装稳定性分析[J]. 海洋工程, 2013, 31(6): 22-29. (BAI Yong, TANG Jiwei, YU Binbin, et al. Installation stability for flexible pipeline by Reel-lay method[J]. The Ocean Engineering, 2013, 31(6): 22-29. (in Chinese))
[12] RUAN Weidong, BAI Yong, CHENG Peng. Static analysis of deepwater lazy-wave umbilical on elastic seabed[J]. Ocean Engineering, 2014, 91:73-83.
[13] 付长静, 李国英, 赵天龙. 海底管道与海床相互作用研究综述[J]. 水利水运工程学报, 2014(6): 100-106. (FU Changjing, LI Guoying, ZHAO Tianlong. On interaction between submarine pipelines and seabed under action of waves[J]. Hydro-Science and Engineering, 2014 (6): 100-106. (in Chinese))
[14] 梁勇, 金志江, 叶皓, 等. 深海钢悬链立管管土相互作用研究进展[J]. 船舶工程, 2013(6): 1-5. (LIANG Yong, JIN Zhijiang, YE Hao, et al. Review of research on interactions of deepwater steel catenary risers with seabed[J]. Ship Engineering, 2013(6): 1-5. (in Chinese))
[15] 王小东, 郭海燕, 高秦岭, 等. 钢悬链线立管触地点区域管土相互作用的有限元分析[J]. 中国海洋大学学报: 自然科学版, 2010 (S1): 197-200. (WANG Xiaodong, GUO Haiyan, GAO Qinling, et al. Finite element analysis of steel catenary riser/seafloor interaction in the touch down zone[J]. Journal of Ocean University of China, Natural Science, 2010 (S1): 197-200. (in Chinese))
[16] 杨辉, 王婷, 雷铮强, 等. 管土接触作用下埋地管道力学分析[J]. 石油矿场机械, 2015 (7): 44-47. (YANG Hui, WANG Ting, LEI Zhengqiang, et al. Analysis on mechanical characteristics of buried pipeline under pipe-soil contact[J]. Oil Field Equipment, 2015 (7): 44-47. (in Chinese))
Mechanical analysis of J-lay pipelaying operation
LIU Dahui, RUAN Weidong, BAI Yong
(Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China)
P751
A
10.16483/j.issn.1005-9865.2017.01.006
1005-9865(2017)01-0051-09
2016-01-17
刘大辉(1980-),男,山东烟台人,硕士,主要从事海洋工程研究。E-mail:daweiping@126.com
阮伟东。E-mail:wdruan@zju.edu.cn
