考虑椭圆化和材料各向异性的管道极限 弯矩承载力解析解研究

王慧平，李 昕，周 晶

(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

考虑椭圆化和材料各向异性的管道极限 弯矩承载力解析解研究

王慧平，李 昕，周 晶

(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

已有的管道极限弯矩承载力解析方法忽略了截面的椭圆化变形，且假设管道截面达到全塑性抵抗力，这对于薄壁管道是不合理的。针对这些不足，在已有解析解的基础上，考虑管道截面塑性区的椭圆化变形以及管道轴向与环向材料的各向异性，推导了管道在内压、轴向力和弯矩联合荷载作用下的极限弯矩承载力解析解。并通过定义材料屈服后不同的广义模量，提出了管道极限弯矩承载力的上限解析解和下限解析解。在此基础上，研究了材料各向异性系数、径厚比以及初始荷载等参数对极限弯矩承载力上限和下限解析解的影响，并得到了一些有益的结论。

管道； 联合荷载；椭圆化；材料各向异性；弯矩承载力；解析解

Abstract: The previous analytic solution ignored the ovalization of the pipe cross-section, and assumed the pipe section able to attain its fully plastic capacity, which seems inappropriate for pipeline with large diameter to thickness ratio. On this basis, by considering the ovalization of the plastic region and the pipe material’s anisotropy of the axial and circumferential direction, an analytical solution of the ultimate bending capacity of pipeline subjected to combined internal pressure, axial forces and bending moments was derived in this research project. Both the lower and upper bound solutions are proposed based on the selection of a general modulus in the process of calculation. Based on the analytical solution, the effect of the anisotropy coefficient, the ratio of diameter to thickness, and the initial loading on moment capacity was studied, and some useful conclusions are obtained.

Keywords: pipeline; combined loading; ovalization; material anisotropy; ultimate bending capacity; analytical solution

随着海洋油气资源的开发，海底管道被广泛应用在海上油气田的开发、生产和产品运输中。海底管道建设日益增多，被称为海上油气田的“生命线”[1-2]。一般情况下，内压荷载是确定海底管道壁厚的控制荷载，而当管道受到滑坡、沉降、地震等影响时，由土体运动引起的弯矩荷载成为管道设计的控制荷载[3-6]。

在过去的四十年间，众多学者致力于联合荷载作用下海底管道的极限弯矩承载力研究。早期的研究主要集中于在内压和轴向力作用下管道极限弯矩承载力的实验研究[7-9]，20世纪开始，众多学者致力于海底管道在复杂荷载作用下的极限弯矩承载力理论研究。20世纪90年代期间，Mohareb和Bai等[10-13]采用Mises屈服准则，基于理想弹塑性假设得到了钢制管道在内/外压和轴向力作用下的极限弯矩承载力解析方程，该解析解被DNV规范[14]采用。Hauch和Bai[15]推导了管道在内压、轴向力和弯矩联合作用下的极限弯矩承载力解析解，并计入了管道材料各向异性系数的影响。随后，Mohareb发展了管道在轴向力、内/外压、扭矩、双轴弯矩和双轴剪力联合作用下的无量纲相互作用方程[16-17], 与他们的实验结果吻合较好[11,18]。党学博等[19]考虑材料各向异性系数的影响，推导出深水海底管道在弯矩、轴向拉力和外压共同作用下的极限承载能力公式，并应用到S型深水铺管施工受力分析中。陈严飞等[20-21]在Mohareb方程的基础上，考虑了管道轴向与环向材料强度的各向异性，提出了腐蚀缺陷管道在内压、轴力和弯矩组合荷载作用下极限弯矩承载力的一组广义解。

实验研究表明[22-24]，Mohareb解析解预测得到的弯矩承载力与实验得到的结果符合较好，具有一定的可靠性且计算简便，因此常被用作实验结果和数值预测结果的基准。然而，Mohareb以及Hauch和Bai[15]的解析方法在推导过程中忽略了截面椭圆化的影响，且假设管道截面达到全塑性抵抗力。这使得解析解无法给出管道在外力作用下的变形特性，且这些假设对于薄壁管道不合理。本文针对这些不足，在Mohareb解析解的基础上，考虑管道截面塑性区椭圆化变形和管道轴向与环向材料强度的各向异性，发展了管道在内压、轴向力和弯矩荷载联合作用下极限承载力解析解。

1 基本假定和屈服准则

1.1基本假定

Mohareb[11,22]，Bai和Hauch[15]推导了管道在内压、轴向力作用下极限弯矩承载力解析解，这里沿用其部分基本假定：1)忽略管道材料塑性部分的应力强化效应；2)在达到极限状态时，塑性中性轴将管道横截面分为压缩和拉伸两个区域；3)不考虑应变局部化的影响。在此基础上，又引入如下假设：1)管道在弯矩作用下，管道的横截面逐渐发生椭圆化变形，但是仍然在同一平面内；2)管道弯曲变形后，曲率半径沿管道截面的变化可以忽略不计，在推导过程中，采用管道截面中心线的曲率半径作为计算值；3)根据受力特性，把屈服后的管道结构简化为拱梁。

1.2屈服准则

管道在内压、轴力和弯矩作用下发生塑性变形时，表现为管道材料在多轴应力下的屈服，其中径向应力和剪应力分量可忽略不计。考虑到管道加工过程中会引起材料轴向和环向的各向异性[25-27]，则轴向应力和环向应力的相互作用方程可表示为[21,28-29]：

由式(1)得到管道轴向压应力和拉应力的极限值：

其中，R为管道的平均半径，t为管壁厚度。

2 内压和轴向力作用下管道极限弯矩承载力解析解

2.1椭圆化应力

在弯曲荷载作用下管道的横截面发生转动变形，进而使轴向压应力σc与轴向拉应力σt产生向内的应力分量qc和qt，如图1所示。qc和qt会使管道横截面发生椭圆化变形，称其为椭圆化应力。根据图1，由平衡方程和几何方程，可得到：

其中，下标c和t分别代表横截面压缩和拉伸区的变量，dsc、dst分别为横截面上压缩和拉伸塑性区的长度，dl为管道小微段长度，ρ为弯曲变形后的曲率半径，θ为管道变形产生的转角，如图1。

由公式(3)和(4)，可得到椭圆化应力：

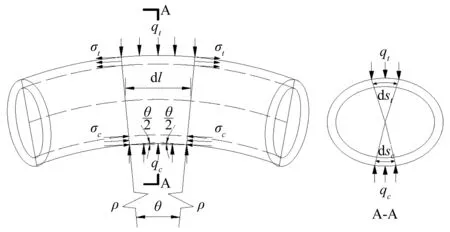
图1 管道截面椭圆化变形机理图Fig. 1 Ovalization mechanism of the pipe cross-section

图2 管道截面在椭圆化应力作用下的变形Fig. 2 Deformation of pipe cross-section under inward stress

2.2弯矩承载力影响系数

在某一弯矩荷载的作用下，假设管道截面的分布为：[αc,π-αt]与[π+αt,2π-αc]为弹性区；[2π-αc,αc]与[π-αt,π+αt]为塑性区，如图2所示。

管道材料刚度越大，截面的椭圆化变形就越小。材料进入塑性后，刚度急剧降低，椭圆化变形与弹性区的椭圆化相比会大很多。为了简化计算，只考虑塑性区的椭圆化变形及其对弯矩荷载的影响，弹性区的椭圆化变形被忽略。因此弹塑性区分界点Ac、Bc、At、Bt的竖向位移为零。在qc与qt的作用下，这些点只有水平向位移，分别移动到Ac'、Bc'、At'和Bt'，如图2所示。为了计算塑性区椭圆化对弯矩承载力的影响，把压缩和拉伸塑性区简化为拱梁结构，如图3所示。

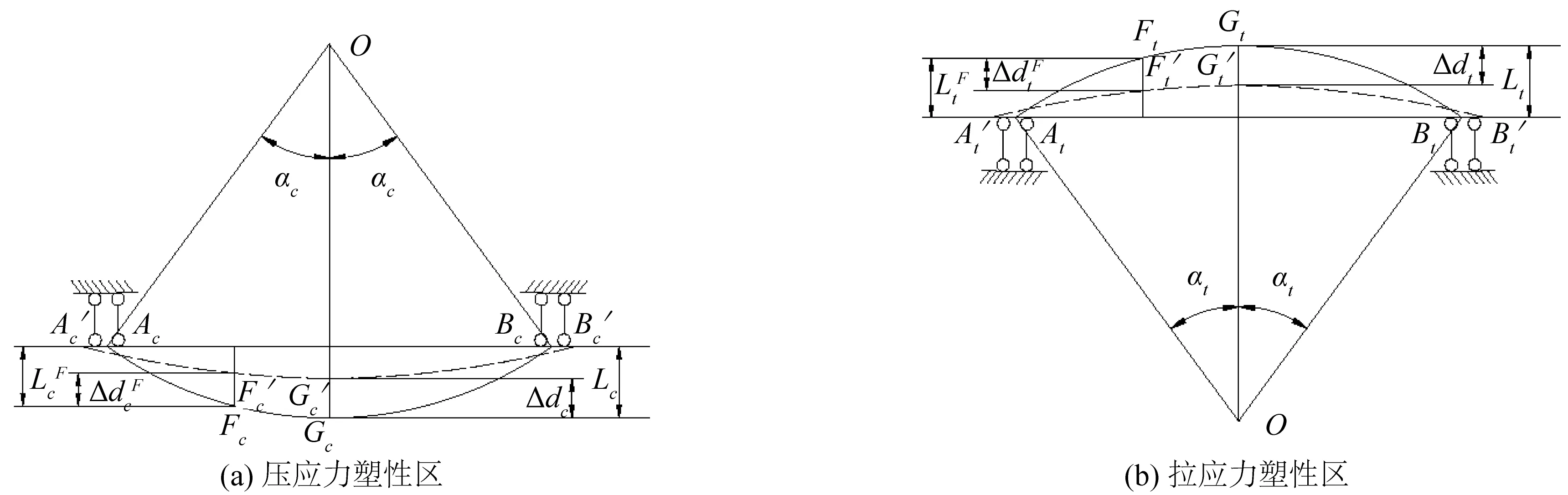
图3 塑性区的简化结构示意Fig. 3 Simplified structures of the plastic regions

在qc与qt作用下，管道截面最外侧点Gc和Gt分别移动到Gc'和Gt'，可求得其竖向位移为：

其中，E'为管道材料屈服后的广义模量，关于E'的讨论见第三部分。

由于Δdc、Δdt相对管道半径R较小，因此可以把塑性区的竖向位移看作是线性变化的。即有：

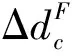
压缩或拉伸塑性区对管道中心线的弯矩可分为两部分：一部分为塑性区对截面弹性与塑性分界线AcBc或AtBt的弯矩；另一部分为从分界线到管道中心线的移轴弯矩。其中第一部分弯矩受椭圆化的影响，而第二部分与椭圆化变形无关。为了得到椭圆化变形后的弯矩承载力，只需求出椭圆化变形对第一部分弯矩的影响即可。椭圆化变形后，塑性区对分界线的弯矩可以表示为：

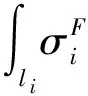
把式(7)代入式(8)中，得到：

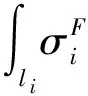
由最小势能原理[31]可知，当壳体结构在内压、轴力和弯矩作用下且处于稳定平衡状态时，不会产生向内凹陷的变形。因此当Δdc>Lc或Δdt>Lt时，令Δdc=Lc，Δdt=Lt。

2.3压缩与拉伸塑性区夹角

若要得到管道横截面的弯矩承载力，还需要求出压缩和拉伸塑性区的夹角αc、αt。图4和图5分别为一般截面应力分布图和相应的轴向变形图。

图4 管道横截面的应力分布Fig. 4 Stress distribution of pipe section

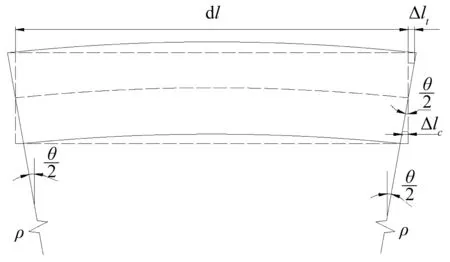
图5 管道截面的轴向变形Fig. 5 Deformation along the axial direction

由图4和图5，可以得到：

其中，E为管道材料的弹性模量，εc和εt为压缩和拉伸弹性区最外侧的轴向应变，Δlc和Δlt为相应的变形，如图5所示。

由式(11)、(12)，可以得到：

2.4管道的弯矩承载力

在计算过程中，将管道横截面的弯矩M分为六部分：M1为受压塑性区对弹塑性分界线的弯矩；M2为受压塑性区从分界线到截面中心线的移轴弯矩；M3为受压弹性区对中心线的弯矩；M4为受拉弹性区对中心线的弯矩；M5为受拉塑性区对分界线的弯矩；M6为受拉塑性区从分界线到中心线的移轴弯矩。对于给定的曲率半径ρ，根据塑性区的位置，可以分为以下四种工况来求解管道的弯矩承载力。

这种工况为管道截面全部在弹性范围内，管道截面最外侧的轴向压应力和拉应力分别为σc'和σt'。与式(11)和(12)类似，有：

根据式(14)和(15)，可得到：

则横截面的轴向力为：

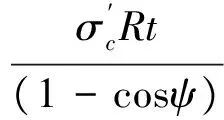
在已知实际轴力的情况下，可根据式(17)采用二分法[32]求出中性轴夹角ψ。从而求出管道截面的弯矩承载力M：

这种工况为仅部分压缩区达到屈服，轴向力可以表示为式(19)，同理可由此确定中性轴夹角ψ。

弯矩承载力M由应力沿整个截面的积分得到：

其中，M4与式(18)中M4相同。

这种工况为仅部分拉伸区达到屈服，此时管道截面轴力F和弯矩M可表示如下：

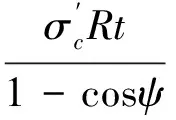
其中，M3与式(18)中M3相同。

这种工况为截面压缩区和拉伸区都达到了屈服，此时管道截面轴向力F和弯矩M可表示为：

其中，M1、M2、M3见式(20)，M4、M5、M6见式(22)。

3 参数分析

由上一节的推导可知，E′是用于求解压缩和拉伸塑性区的竖向位移Δdi的一个材料参数，见式(6)。管道材料进入塑性后，应力-应变曲线是非线性的，材料的切线模量不断变化。为了求出考虑椭圆化的弯矩承载力，在计算过程中可以引入一个确定的E′值来代替不断变化的切线模量，称为屈服后的广义模量。从物理意义上讲，E′的取值范围应该在应变强化模量Et和弹性模量E之间，其中Et为材料的应力-应变曲线上屈服点和极值点连线的斜率。因此，E′=Et和E′=E分别代表管道下限解析解和上限解析解。与前人的实验结果以及有限元计算结果的对比表明[33]，理论推导所得到的下限解和上限解可以很好地预测管道的极限弯矩承载力。

下面开展管道极限弯矩承载力的参数分析，分别研究了材料各向异性系数α、径厚比D/t以及初始荷载对极限弯矩承载力上限解析解和下限解析解的影响，其中初始荷载包括初始内压和初始轴向力荷载。计算管道的几何参数为：直径508 mm，壁厚7.9 mm，弹性模量196 110 MPa。

3.1各向异性系数α对极限弯矩荷载的影响

研究X80管道在不同内压和轴向压力作用下，各向异性系数对极限弯矩承载力的影响。表1给出了不同计算工况下，管道材料环向和轴向的屈服强度、抗拉强度以及管道材料的各向异性系数[27]。图6给出了不同内压作用下，管道的弯矩承载力的下限值和上限值。其中，P代表管道承受的内压作用力，M代表管道的弯矩承载力。

从图6可以看出，当各向异性系数为0.5，即材料为各向同性时，材料的屈服应力越高，管道的极限弯矩承载力越大。当材料的环向屈服强度相同时，管道的弯矩承载力随轴向屈服强度的增大而增大。当材料的轴向屈服强度相同时，环向屈服强度对弯矩承载力的影响与内压值有关：内压值越大，环向屈服强度的影响也越大，且管道的弯矩承载力随环向屈服强度的增大而有所提高。

这里还计算了不同轴向力作用下，管道弯矩承载力的下限值和上限值。理论上来说，管道在轴向力和弯矩共同作用下的承载力只与管道的轴向屈服强度有关，与环向屈服强度无关，这与本文的解析结果相同。由于篇幅的限制，这里没有列出相应的计算结果。

表1 X80管道材料参数Tab. 1 Material properties for X80 pipe

图6 内压作用下各向异性系数对弯矩荷载的影响Fig. 6 Effect of anisotropy coefficient on the moment capacity under internal pressure

图7 径厚比对弯矩承载力的影响Fig. 7 Effect of radio of D/t on moment capacity

3.2径厚比D/t对极限弯矩荷载的影响

工程中使用的管道的径厚比D/t大多为30～100，因此在直径不变的基础上计算了八种不同径厚比的管道，分别为30、40、50、60、70、80、90、100。管道的材料参数取为工况1，α=0.5。图7给出了在纯弯矩作用下，管道极限弯矩承载力下限值和上限值随径厚比的变化情况。

从图7中可以看出，管道的极限弯矩承载力随着径厚比的增大而减小。在径厚比相对较小的情况下，管道的弯矩承载力随径厚比的增大急剧减小，当径厚比较大时，弯矩承载力的变化趋势逐渐趋于平缓。上限值和下限值的变化趋势一致。

3.3初始荷载对极限弯矩荷载的影响

图8给出了在不同的轴向力作用下，无量纲的内压对极限弯矩承载力下限值和上限值和的影响。其中，P与F为管道实际的内压和轴向力荷载，Py与Fy为管道的屈服内压和屈服轴力，Py=2σyt/D，Fy=σyA，A为管道截面面积。F/Fy为负值代表管道承受轴向压力，F/Fy为正值代表管道承受轴向拉力。

从图8中可以看出，无论是下限还是上限解析解，轴向压力会大大降低管道内压荷载的作用范围，而轴向拉力会增加内压荷载的作用范围。对于无轴向力作用或承受轴向压力作用的管道，随着内压荷载的增加，管道的极限弯矩承载力会逐渐降低；对于承受轴向拉力作用的管道，随着内压荷载的增加，管道的极限弯矩荷载表现为先增加后减小的趋势。

从图8中还可以看出，对于无内压作用的管道，当承受相同的轴向拉力和轴向压力时，管道的弯矩承载力也是相同的，也就是说在无压状态下轴向拉力和轴向压力对管道的极限弯矩承载力的削弱程度相同。

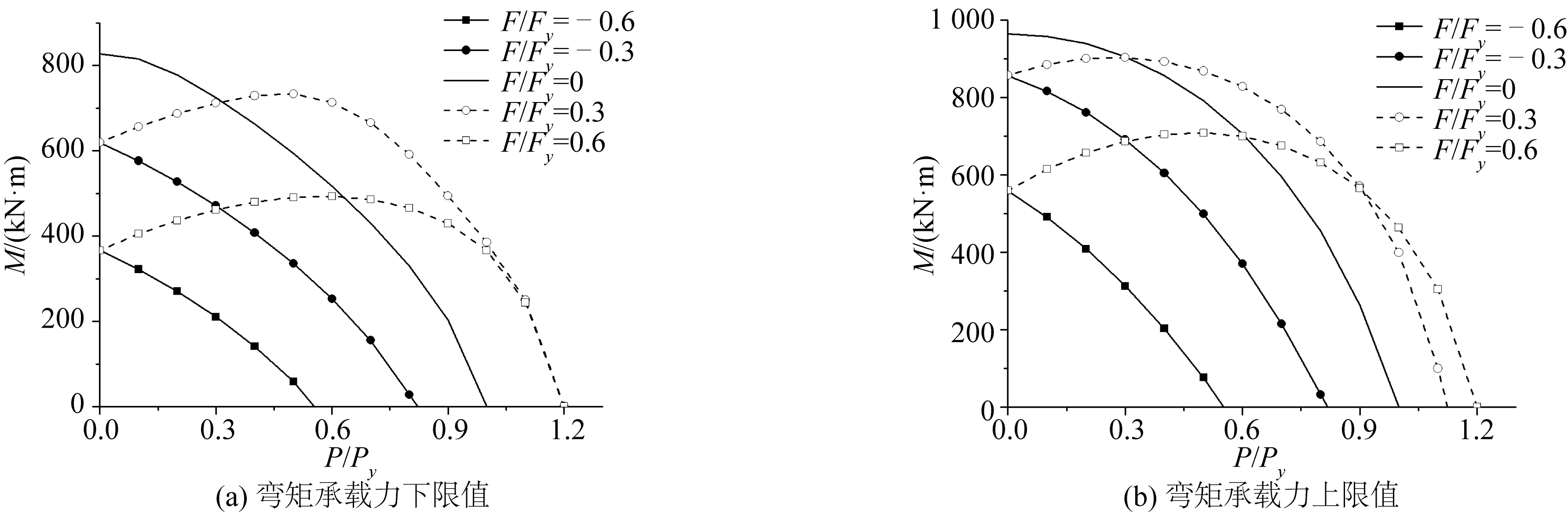
图8 内压、轴向力对极限弯矩荷载的影响Fig. 8 Effect of axial force and internal pressure on moment capacity

4 结 语

考虑管道截面塑性区椭圆化以及材料各向异性的影响，发展了在内压和轴向力组合荷载作用下管道的极限弯矩承载力上限和下限解析解，并研究了材料各向异性系数、径厚比、初始内压和轴向力荷载对管道极限弯矩承载力的影响。得到如下结论：

1)管道材料为各向同性时，材料的屈服应力越高，管道的极限弯矩承载力越大。

2)当无内压作用时，管道的极限弯矩承载力只与管道的轴向屈服强度有关，与环向屈服强度无关。当有内压作用时，各向异性系数对管道的极限弯矩承载力有一定的影响。内压值越大，环向屈服强度对弯矩承载力的影响也越大，且管道的弯矩承载力随环向屈服强度的增大而有所提高。

3)管道的极限弯矩承载力随着径厚比的增大而减小。在径厚比相对较小的情况下，管道的弯矩承载力随径厚比增大急剧减小，当径厚比较大时，弯矩承载力的变化趋势逐渐趋于平缓。

4)对于无轴向力作用或承受轴向压力作用的管道，随着内压荷载的增加，管道的极限弯矩承载力会逐渐降低；对于承受轴向拉力作用的管道，随着内压荷载的增加，管道的极限弯矩荷载表现为先增加后减小的趋势。

5)对于无内压作用的管道，轴向拉力和轴向压力对管道极限弯矩承载力的削弱程度是相同的。

[1] 周晶,冯新,李昕.海底管线全寿命安全运行的关键问题研究[J].工程力学, 2011, 28(S2):97-108. (ZHOU J, FENG X, LI X. Reasearch on critical issues of life-cycle service safety for subsea pipelines[J].Engneering Mechanics, 2011, 28(S2):97-108.(in Chinese))

[2] PALMER A C, KING R A. Subsea pipeline engineering[M]. Tulsa: Penn Well Books, 2004.

[3] 王慧平,李昕,周晶.初始几何缺陷对管道极限承载力影响研究[J].海洋工程,2014,32(5):50-56. (WANG H P, LIN X, ZHOU J. Effects of initial imperfections on pipeline capacities[J]. The Ocean Engineering, 2014, 32(5):50-56. (in Chinese))

[4] 陈严飞.海底腐蚀管道破坏机理和极限承载力研究[D].大连:大连理工大学,2009. (CHEN Y F. Study on failure mechanism and ultimate load capacity of corroded submarine pipeline[D]. Dalian:Dalian University of Technology,2009. (in Chinese))

[5] KARAMPOUR H, ALBERMANI F, VEIDT M. Buckle interaction in deep subsea pipelines[J]. Thin-walled Structures, 2013, 72:113-120.

[6] LIU R, XIONG H, WU X L, et al. Numerical studies on global buckling of subsea pipelines[J]. Ocean Engineering, 2014(78):62-72.

[7] BOUWKAMP J G, STEPHEN R M. Large diameter pipe under combined loading[J]. Journal of Transportation Engineering, 1973, 99(TE3): 521-536.

[8] SHERMAN D R. Test of circular steel tubes in bending[J]. Journal of the Structural Division, 1976,102 (ST11): 2181-2195.

[9] SCHNEIDER P S. Flexural capacity of pressurized steel pipe[J]. Journal of Structural Engineering,1998,124(3), 330-340.

[10] MOHAREB M E, ELWI A E, KULAK G L, et al. Deformational behaviour of line pipe[R]. Canada: University of Alberta, 1995.

[11] MOHAREB M,MURRAY D W. Mobilization of fully plastic moment capacity for pressurized pipes[J].Journal of Offshore Mechanics and Arctic Engineering,1999,121(4):237-241.

[12] BAI Y, IGLAND R, MOAN T. Tube collapse under combined pressure,tension and bending[J].International Journal of Offshore and Polar Engineering,1993,3(2):121-129.

[13] BAI Y, IGLAND R, MOAN T. Tube collapse under combined external pressure,tension and bending[J].Journal of Marine Structures,1997,1(5):389-410.

[14] DNV.Rules for submarine pipeline system[S]. Norway: Det Norske Veritas,1996.

[15] HAUCH S R, BAI Y. Bending moment capacity of pipes[J]. Journal of Offshore Mechanics and Arctic Engineering, 2000,122(4):243-252.

[16] MOHAREB M. Plastic Interaction relations for pipe sections[J]. Journal of Engineering Mechanics,2002,128(1): 112-120.

[17] MOHAREB M. Plastic resistance of pipe sections: upper bound solution[J]. Journal of Structure Engineering, 2003,129(1):41-48.

[18] OZKAN I F, MOHAREB M. Testing of steel pipes under bending,twist,and shear[J]. Journal of Structural Engineering,2003,129(10):1350-1357.

[19] 党学博, 龚顺风, 金伟良, 等. 深水海底管道极限承载能力分析[J]. 浙江大学学报:工学版, 2010, 44(4): 778-782. (DANG X B, GONG S F, JIN W L, et al. Analysis on ultimate bearing capacity of deepwater submarine pipe[J]. Journal of Zhejiang University, Engineering Science, 2010,44(4):778-782. (in Chinese))

[20] 陈严飞，李昕，周晶. 不规则腐蚀缺陷管道极限承载力研究[J]. 工程力学，2009, 26(11): 190-196. (CHEN Y F, LI X, ZHOU J. Ultimate bending capacity of pipe with arbitrary corrosion defects[J]. Engineering Mechanics,2009, 26(11): 190-196. (in Chinese))

[21] 陈严飞，李昕，周晶. 组合荷载作用下腐蚀缺陷管道的极限承载力[J].计算力学学报，2011, 28(1):132-139. (CHEN Y F, LI X, ZHOU J. Ultimate flexural capacity of pipe with corrosion defects subject to combined loadings [J]. Chinese Journal of Computational Mechanics, 2011, 28(1):132-139. (in Chinese))

[22] MOHAREB M, KULAK G L, ELWI A, et al. Testing and analysis of steel pipe segments[J]. Journal of Transportation Engineering, 2001, 127(5): 408-417.

[23] DOREY A B, CHENG J J R, MURRAY D W. Critical buckling strains in energy pipelines[R]. Department of Civil and Environmental Engineering, University of Alberta, 2001.

[24] OZKAN I F, MOHAREB M. Testing and analysis of steel pipes under bending, tension, and internal pressure[J]. Journal of Structural Engineering, 2009, 135(2): 187-197.

[25] PALMER A C, KING R A. Subsea pipeline engineering[M].Tulsa: Penn Well Books, 2004.

[26] 陈文，刘清友，孙新军，等．降低管线钢拉伸强度各向异性的热轧工艺[J]. 钢铁研究学报，2010, 22(12): 53-57. (CHEN W, LIU Q Y, SUN X J, et al. Hot rolling technology to reduce tensile strength snisotropy of pipeline steel[J]. Journal of Iron and Steel Research, 2010, 22(12): 53-57. (in Chinese))

[27] 郑茂盛, 李金波, 李海军. X80级管线钢的各向异性特征[J]. 焊管, 2005, 28 (3): 13-16. (ZHENG M S, LI J B, LI H J. The anisotropic of the X80 pipeline[J]. Welded Pipe,2005, 28 (3): 13-16. (in Chinese))

[28] 徐秉业，刘信生．应用弹塑性力学[M]. 北京：清华大学出版社，1995. (XU B Y, LIU X S. Application of elastic-plastic mechanics[M]. Beijing: Tsinghua University Press，1995. (in Chinese))

[29] HILL R. The mathematical theory of plasticity[M]. Oxford: Oxford University Press，1998．

[30] KYRIAKIDES S, CORONA E. Mechanics of offshore pipelines[M]. Elsevier Ltd., 2007．

[31] 龙驭球，包世华，匡文起，等. 结构力学[M]．北京：高等教育出版社, 2001. (LONG Y Q, BAO S H, GUANG W Q, et al. Structural mechanics[M]. Beijing: Higher Education Press,2001. (in Chinese))

[32] 张宏伟，金光日，施吉林，等. 计算机科学计算[M].北京：高等教育出版社，2005. (ZHANG H W, JIN G R, SHI J L, et al. Computer science calculation[M].Beijing: Higher Education Press,2005. (in Chinese))

[33] WANG H P, LI X, ZHOU J. Ultimate bending capacities of steel pipelines under combined loadings[J]. Advances in Structural Engineering, 2016, 19(4): 642-659.

Analytical solution of ultimate bending capacity of pipeline considering ovalization and material anisotropy

WANG Huiping, LI Xin, ZHOU Jing

(State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China)

TE973；P756.2

A

10.16483/j.issn.1005-9865.2017.01.008

1005-9865(2017)01-0071-09

2016-01-15

国家重点基础研究发展计划(973计划)(2011CB013702); 新世纪优秀人才支持计划资助(NCET-11-0051)

王慧平(1985-)，女，吉林长春人，博士研究生，主要从事海底管道承载能力的研究。E-mail：whpwanghuiping@126.com

李 昕。E-mail：lixin@dlut.edu.cn