API X70和X80管线钢管屈服强度的双循环模拟试验分析和估算*

方 伟，吕 华，徐 婷，许晓锋 编译

（中国石油集团石油管工程技术研究院，西安 710077）

API X70和X80管线钢管屈服强度的双循环模拟试验分析和估算*

方 伟，吕 华，徐 婷，许晓锋 编译

（中国石油集团石油管工程技术研究院，西安 710077）

为了准确估算API X70和X80管线钢管的屈服强度，分别对API X70和X80管线钢板和钢管进行了制管和压平过程的双循环模拟试验，并将包申格应力参数和Swift方程相结合来估算钢管的屈服强度。试验和估算结果表明，包申格应力参数和Swift方程相结合的估算方法中已经包含了显微组织和制管过程的影响因子，因而能较为准确地估算钢管的屈服强度。因拉压强度差效应较小且和反向流动曲线可用一条曲线表示，因此利用展平钢板的拉伸/压缩性能可有效估算制管前后屈服强度的变化，该估算方法对控制显微组织和制造工艺参数进而控制管线钢板的屈服强度有着重要的作用。

焊管；冷加工；力学性能；包申格效应；双循环模拟试验

Abstract:In order to accurately estimate the yield strengths of API X70 and X80 linepipe steel pipes,a double-cycle simulation test for the piping and flattening processes was respectively conducted to estimate the yield strength.The simulation test results indicated that the yield strengths of the outer or inner wall of the pipe could be estimated by combination of Swift’s equation and the Bauschinger stress parameter,and that these estimated yield strengths were well matched within a small error range with the measured yield strengths.Thus,the variations in yield strength before and after the piping could be effectively estimated using the tension/compression properties of the leveled sheets because the strength differential effect was small and the reverse flow curves were expressed by a single curve.These findings suggested that the present estimation method played an important role in controlling microstructural and manufacturing process parameters to minimize the reduction in yield strength of the linepipe steel sheets.

Key words:welded pipe;cold working;mechanical properties;Bauschinger effect;double-cycle simulation test

1 概 述

管线钢管用于长距离输送原油或天然气，通常需要具有较高强度以承受输送介质的高压。美国石油学会（API）推荐在制管和压平工艺后可通过拉伸试验评价钢管的强度。在制管和压平过程中，钢管外壁和内壁经受不同的应变，即外壁为拉伸－压缩应变，内壁为压缩－拉伸应变。根据以往的经验，由钢管压平至钢板的屈服强度通常比由热轧板卷展平至钢板的屈服强度低。如果采用热轧板卷展平至钢板的屈服强度来预评估钢管压平至钢板的屈服强度，往往会导致大多数制造商家提供的管线钢管不能满足API标准的要求。

在反复拉伸和压缩加载情况下（如制管和压平），屈服强度降低的原因一般可用包申格效应来解释。Park和Jeo研究了API X46～X70管线钢的包申格效应，定量分析了显微组织对制管后屈服强度变化的影响。制管后的屈服强度还可能随制管工艺和变形量的变化而变化。近期，Yun和Chang对X70管线钢制管后的屈服强度进行了估算。在X80或更高强度管线钢中，其显微组织相当复杂，但主要由低温转变的显微组织如针状铁素体等组成。螺旋焊或电阻焊的制管工艺复杂且影响因素较多，很难精确估算制管前后屈服强度的变化。因此，通过定量评价，并结合应变硬化和包申格效应分析制管前后屈服强度的变化，对于精确估算钢管的屈服强度，保证管线钢管质量的稳定是非常必要的。

采用控制轧制工艺，在一定的冷却条件下，分别制造一卷API X70钢板和两卷具有不同显微组织的X80钢板，再用螺旋焊和电阻焊工艺分别将其制成钢管后，取样压平，测试其屈服强度。制管和压平过程采用的是拉伸－压缩－拉伸或压缩－拉伸－拉伸的双循环模拟试验，由此估算屈服强度，并与压平钢板实测的屈服强度进行比较。通过试验及测试结果，估算钢管外壁和内壁的屈服强度，以验证制管后屈服强度估算方法的可行性。

2 试验方法

2.1 钢板和制管工艺

本研究使用的钢板是一卷API X70钢板和两卷最低屈服强度分别为483 MPa和552 MPa的X80钢板。为方便标识，制成螺旋焊管的X70和X80钢板的试样编号分别标记为S7和S8，制成电阻焊管的X80钢板的试样编号标记为E8。试验用API X70和X80钢的化学成分见表1。

钢板轧制时，采用高轧制压下率（80%以上）以期达到整体晶粒细化的效果。轧制完成后，迅速冷却并盘卷，然后再将热轧板卷展平。将X70和X80钢板采用与轧制方向呈30°的螺旋焊工艺分别制成Φ1 020 mm和Φ1 220 mm钢管，将另一卷X80钢板采用与轧制方向呈90°的电阻焊工艺制成Φ510 mm钢管。API X70和X80钢的轧制和制管条件见表2。

表1 API X70和X80钢的化学成分 %

表2 API X70和X80钢的轧制和制管条件

2.2 显微组织分析

将展平钢板抛光，并用2%硝酸溶液腐蚀，用光学显微镜和扫描电镜观察纵横向截面显微组织。用图像分析仪测量钢板中显微组织的体积分数。

2.3 拉伸试验

在展平钢板和由钢管压平至钢板的壁厚中间位置截取拉伸试样，取样方向和位置如图1所示。螺旋焊管和电阻焊管与轧制方向分别呈30°和90°。制备直径为6 mm、标距长度为30 mm的圆棒试样，用100 kN万能试验机按ASTM标准试验方法以5×10-3s-1的应变速率在室温下试验。载荷下0.5%伸长率时的应力为有连续屈服行为的钢的屈服强度，而下屈服点为有不连续屈服行为的钢的屈服强度。

图1 拉伸试样和双循环模拟试验取样方向和位置示意图

2.4 估算钢管屈服强度的双循环模拟试验

制管过程中变形量对钢管的力学性能有很大的影响，本研究进行了制管和压平过程的拉伸－压缩－拉伸（简称 T－C－T）或压缩－拉伸－拉伸（简称C－T－T）的双循环模拟试验。在制管和压平过程中，钢管外壁和内壁经受不同的应变，因此在拉伸试验前进行拉伸－压缩和压缩－拉伸试验，分别模拟外壁和内壁的应变状态。在展平钢板的壁厚中间位置截取双循环模拟试验试样，取样方向同展平钢板或由钢管压平至钢板的拉伸试样（见图1）。以往的试验结果表明，30°和90°方向拉伸性能具有各向异性，但包申格效应差异很小。用万能试验机按ASTM标准试验方法对直径为6.35 mm、标距长度为12.5 mm的圆棒试样进行拉伸试验，用12.5 mm长的引伸计控制并测量模拟应变。

制管和压平过程中应变梯度随钢板厚度的变化而变化，距钢板厚度中心X处的应变梯度可表示为

式中：ε（X）—距离X处的应变；

D—钢管外径；

t—钢板厚度；

X—距钢板厚度中心的距离。

考虑到应变随钢板厚度的位置而变化，制管和压平过程的模拟试验采用1%、2%、3%和4%的预应变。通过该试验对屈服强度进行估算，并与压平钢板测得的实际屈服强度进行比较。

3 试验结果

3.1 API X70和X80管线钢板的显微组织

3个试样的扫描电镜照片如图2所示。由图2可见，试样由准多边形铁素体（QPF）、针状铁素体（AF）、 粒状贝氏体（GB）、 珠光体（P）和马氏体-奥氏体（MA）组分组成。准多边形铁素体强度相对较低，但韧性较高；针状铁素体是一种具有高强度兼有高韧性的显微组织；粒状贝氏体韧性低；珠光体强度高；MA组分是在较快的冷却速率下形成的二次相，且具有高强度和低韧性。

对试样中各种显微组织进行分类统计，结果见表3。由表3可以看出，S7和E8试样由准多边形铁素体、针状铁素体、粒状贝氏体及少量珠光体和MA组成，E8试样中的针状铁素体和粒状贝氏体的体积分数较高。

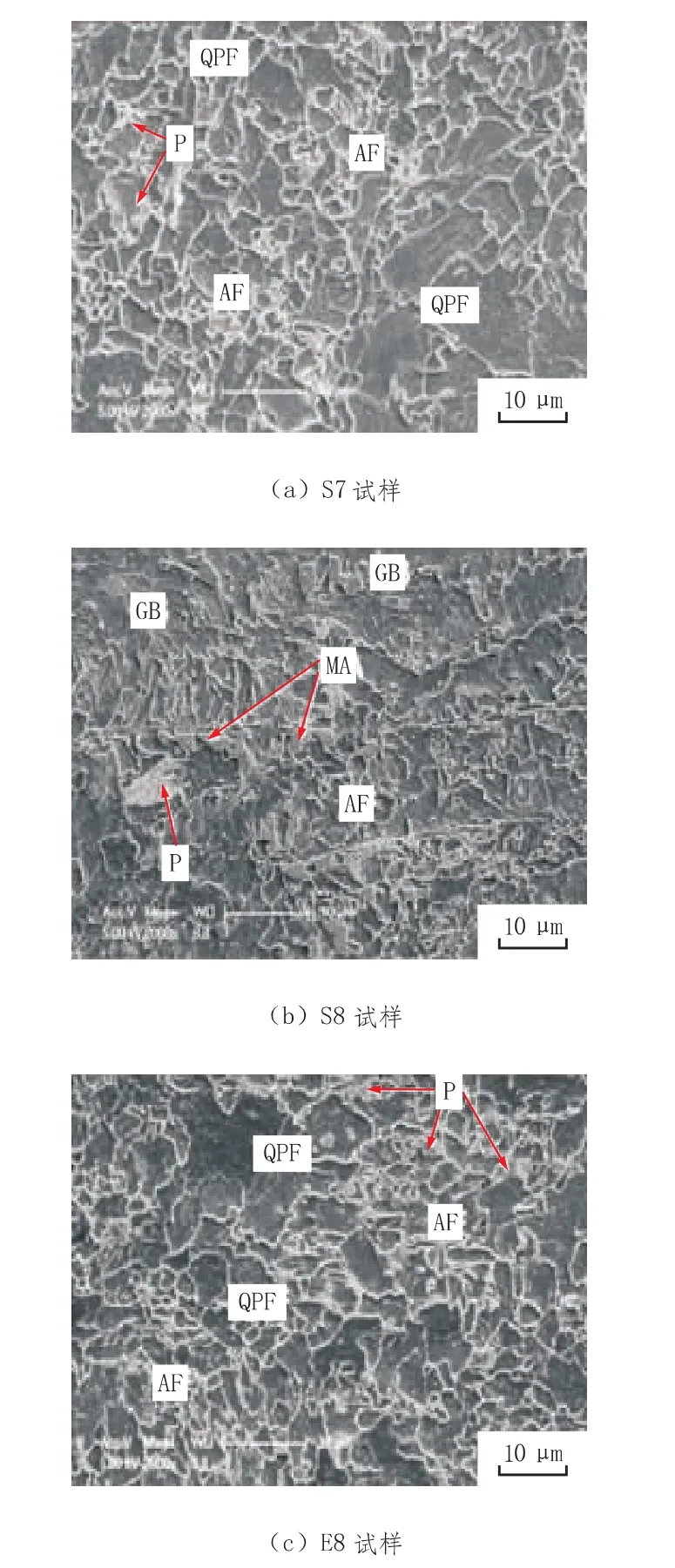
图2 S7、S8和E8酸蚀试样的SEM显微照片

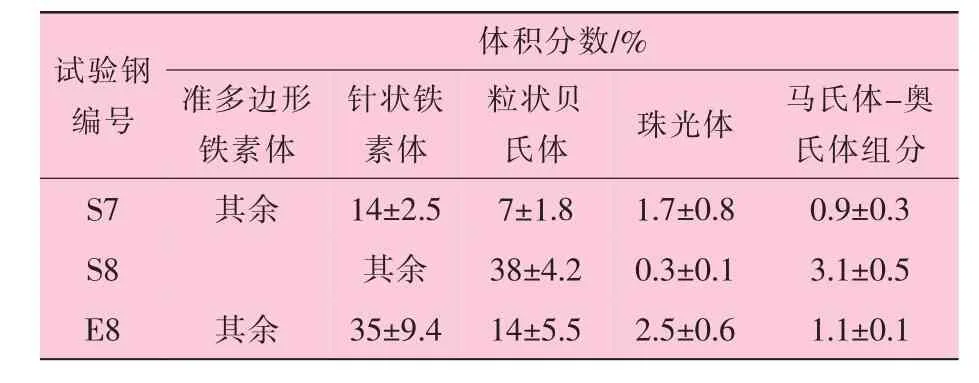
表3 API X70和X80钢中各种显微组织的体积分数

SEM显微照片中的MA组分和其他显微组织之间很难区分，因此将试样在LePera溶液中浸蚀。经过浸蚀的S7、S8和E8试样的光学显微照片如图3所示。图3中MA组分和其他显微组织（QPF、AF、GB 和 P）分别用亮白色和棕色进行着色。

3.2 通过双循环模拟试验估算钢管外壁屈服强度

图3 LePera溶液浸蚀后S7、S8和E8试样的光学显微镜照片

展平钢板和由钢管压平至钢板的屈服强度检测结果见表4。典型的双循环模拟试验曲线如图4所示。图4中包括拉伸、压缩、拉伸曲线以及预应变（εpre1、εpre2）、 预应变对应的流动应力、 拉伸屈服应力（εy1、εy3）和压缩屈服应力（εy2）。 当反转由反向加载状态获得的下行压缩曲线时，可以看见整个应变过程。从这些曲线就可以确定包申格应力的参数为

表4 API X70和X80展平钢板和由钢管压平至钢板的屈服强度

图4 典型的双循环模拟试验曲线

本研究用BS对包申格效应进行量化。

在制管和压平过程及随后的展平钢板的拉伸试验过程中，钢管外壁受到拉伸－压缩－拉伸应变，且当展平钢板在拉伸－压缩和压缩－拉伸加载模式下受力时，出现两次包辛格效应（见图 4）。快速变形过程中包申格效应随预应变（εpre）变化，因此用1%、2%、3%和4%的预应变来模拟制管和压平过程。E8试样双循环模拟试验获得的应力－应变曲线如图5所示，图5中红色压缩曲线显示出与快速变形曲线不同的行为。包申格效应导致的屈服强度的降低，以及应变硬化效应，流动压力突然增加（瞬变部分），快速变形（稳定部分）的流动应力显示出类似的增加，这些结果均与先前的结果相吻合。预应变分别为1%、2%、3%和4%时的压缩曲线如图6所示。由图6可见，压缩曲线的流动行为几乎是相同的，与拉伸预应变无关。

图5 E8试样外壁双循环模拟试验曲线

图6 预应变为1%、2%、3%和4%时的压缩曲线

可用本构方程将图6中这些相似的流动曲线方程化。表示塑性行为的主要本构方程有Hollomon方程和Swift方程。由于Swift方程中有一个材料常数b作为补充项，因而Swift方程比Hollomon方程更能准确地表示塑性行为。Swift方程为

式中：σ—流动应力；

εp—塑性应变；

a—强度指数；

b—材料常数；

N—加工硬化指数。

将压缩曲线与Swift方程拟合可获得这些常数。当拉伸预应变为2%、压缩预应变为4%的压缩曲线与Swift方程拟合时，可得到下列方程

与Swift方程拟合获得的压缩曲线如图7所示，将拟合曲线与试验获得的压缩曲线进行比较，可见这两条曲线的吻合度较高。

图7 与Swift方程拟合获得的压缩曲线和试验获得的E8试样外壁压缩曲线对比

在拉伸－压缩－拉伸试验中压缩－拉伸加载的包申格效应可用第二个包申格应力参数（2ndBS）进行量化（见图4）。E8试样外壁压缩预应变与2ndBS的关系如图8所示。在图8（a）中，变形初始阶段2ndBS突然增大，但随后增量逐渐减少，这是因为压缩－拉伸加载的包申格效应受拉伸－压缩－拉伸试验中两次包申格效应的影响，在给定压缩预应变情况下，2ndBS随着拉伸预应变的增加而减小。图8（b）是压缩预应变与2ndBS的对数关系，可见在对数坐标内2ndBS与压缩预应变成正比关系，故可用（5）式表示。

图8 E8试样外壁压缩预应变与2ndBS的关系

由钢管压平至钢板的屈服强度就是拉伸－压缩－拉伸试验的最后一条拉伸曲线的屈服强度（见图5中绿色虚线圆圈所示）。Swift方程和2ndBS方程结合可估算出该屈服强度值。式 （2）中，包申格应力参数由快速加载的流动应力和反向加载的屈服强度构成，因而反向加载的屈服强度可以表示为

式（6）中σpre是图5中压缩曲线的最大应力，可由 Swift方程的式（4）得到。将式（4）和式（5）代入式（6）， 可得到式（7）。

式（7）中，因钢管压平需要X%的应变，εp可由式（1）获得。 因此将式（1）代入式（7）可得到 E8试样由钢管压平至钢板的外壁屈服强度σy外。

用与E8试样相同的方法计算S7和S8试样的Swift方程和2ndBS方程，结果见表5。S7和S8试样由钢管压平至钢板的外壁屈服强度分别用式（9）和式（10）表示。

表5 API X70和X80钢的Swift方程和包申格应力参数方程

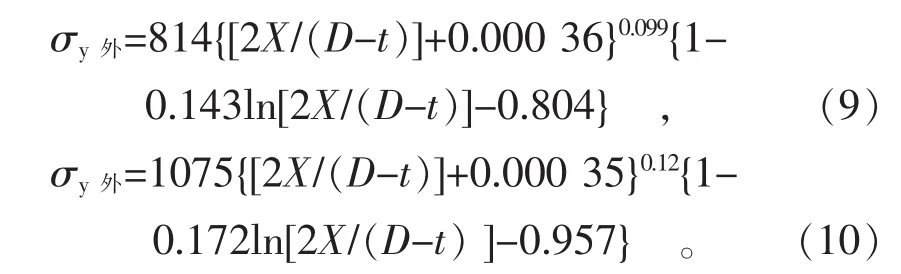
3.3 通过模拟试验估算钢管内壁屈服强度

在制管和压平过程及随后展平钢板的拉伸试验过程中，钢管内壁受到压缩－拉伸－拉伸应变，包申格效应发生在压缩－拉伸加载过程中展平钢板产生应变时。用1%、2%、3%和4%的预应变模拟制管和压平过程，由E8试样的双循环模拟试验获得的应力－应变曲线如图9所示。图10为钢管内壁的拉伸和压缩曲线、变形行为和1stBS。在压缩－拉伸－拉伸曲线中，第一条拉伸曲线（红线）显示了瞬变部分和稳定部分，其流动行为几乎相同，与压缩预应变无关（见如图 10（a））。该流动行为与图6（a）的外壁拉伸－压缩－拉伸曲线中的压缩曲线（见图10（b））流动行为也类似。这是因为X70和X80钢的拉伸和压缩行为主要与位错的结构和移动性有关。在快速变形过程中，这些钢具有拉伸－压缩对称性，表现为相同的变形行为，无论拉伸或压缩变形方向如何（见图 10（c））。 因此， 1stBS在压缩－拉伸－拉伸和拉伸－压缩－拉伸曲线中是相同（见图10（d）），因为包申格效应在两条曲线中的作用是一样的。出现相同的流动曲线时很容易估算钢管内壁的屈服强度。

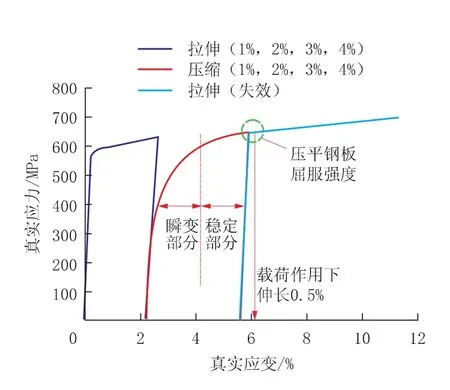
图9 E8试样内壁的双循环模拟试验曲线

图10 E8试样内壁的拉伸和压缩曲线、变形行为和1stBS

因压缩－拉伸－拉伸曲线中的第一条拉伸曲线与外壁的拉伸－压缩－拉伸曲线中的压缩曲线相同（见图10（b）），因此用于外壁屈服强度估算的Swift方程也可用于内壁屈服强度的估算。E8试样的压缩－拉伸－拉伸曲线中第一条拉伸曲线的Swift方程同样可以用式（4）表示。

不同于外壁屈服强度的估算，内壁屈服强度的估算可不考虑包申格应力参数。这是由于拉伸－拉伸应变过程中，包申格效应对第二条拉伸曲线几乎没有影响，另外第二条拉伸曲线的流动行为与第一条拉伸曲线相同。用载荷下产生0.5%伸长率时的应力或0.2%残余应变方法直接测量屈服强度。在用载荷下产生0.5%伸长率确定应力的方法中，从拉伸曲线可获得应变值，而0.2%残余应变方法在测量每种待测材料的弹性模量时有些困难。因此，给Swift方程（4）中增加0.5%应变项来估算屈服强度，具体计算见式（11）。

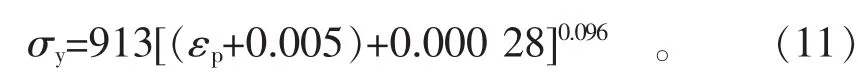
将式（1）代入式（11）得到式（12）， 用于估算内壁的屈服强度。

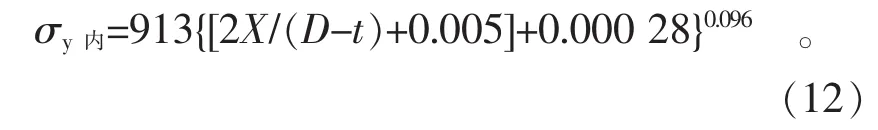
用与E8试样相同的方法计算S7和S8试样的Swift方程和2ndBS方程，结果见表5。S7和S8试样由钢管压平至钢板的内壁屈服强度可用Swift方程、BS方程和预应变方程分别表示为

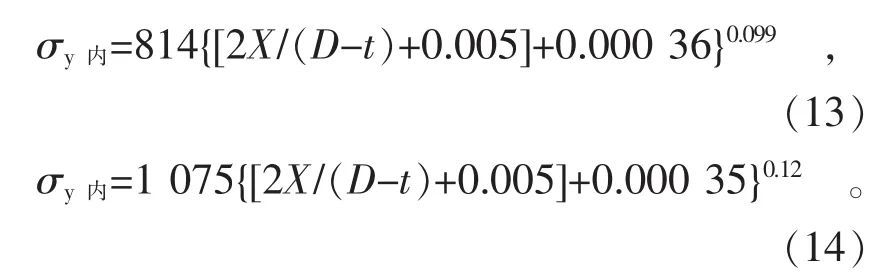
3.4 估算和测试的屈服强度比较

计算的S7、S8和E8试样由钢管压平至钢板的屈服强度如图11所示。3个试样中，在拉伸－压缩和压缩－拉伸曲线中出现了两次包申格效应，因此外壁的屈服强度低于内壁的屈服强度。随着测量点从中心向外壁移动，因制管和压平过程中预应变增加，屈服强度降低；随着测量点从中心向内壁移动，因两次拉伸加载产生的应变硬化效应覆盖了一次包申格效应，屈服强度增加。另外，由电焊管制成的E8试样具有较大的制管应变（t/D）（由于外径较小），因此，E8试样比S7和S8试样的屈服强度变化量更大。

图11 计算的S7、S8和E8试样由钢管压平至钢板的屈服强度

在图11中距中心间隔±3 mm范围内取平均值时，估算的S7、S8和E8试样的屈服强度分别为492 MPa、586 MPa和555 MPa。 这些数据与测量的由钢管压平至钢板的屈服强度（表4中的504 MPa、586 MPa和530 MPa）吻合的较好，误差不超过4.7%。

4 讨 论

4.1 显微组织对屈服强度的影响

当展平钢板经过制管过程时，对钢板沿不同厚度位置施加拉伸或压缩应力，钢管的屈服强度由应变硬化效应和包申格效应的竞争机制确定。钢管的应变硬化性能如图12所示。S7和E8试样的显微组织主要由准多边形铁素体组成，因此具有类似的应变硬化性能；S8试样的显微组织是针状铁素体基体中含有MA组分，因此具有相当高的应变硬化性能（见图12（a）），主要由准多边形铁素体组成的S7和E8试样具有类似的应变硬化性能，而在针状铁素体基体中含有MA组分的S8试样具有相当高的应变硬化性能（图12（a））。S8试样的高应变硬化性能与主要组织为针状铁素体有关。S8试样的1stBS高于S7和E8试样，而S7和E8试样的1stBS几乎相同（见图12（b））。由此可见，包申格效应对S8试样的作用比S7和E8试样更显著。

图12 钢管的应变硬化性能

将S7和S8试样进行比较时，S7试样由钢管压平至钢板的屈服强度比展平钢板的屈服强度低8 MPa，而 S8试样则高 26 MPa（见表 4）。S7试样中，包申格效应突然增加时屈服强度降低，而应变硬化效应并不大。S8试样中，应变硬化效应相当大时屈服强度增加，而在制管应变小于2%的情况下包申格效应与S7试样差别不大。这些结果表明，含有针状铁素体和MA组分的试样（如S8试样）在相同的制管工艺条件下可使屈服强度的降低达到最小，因其应变硬化效应大于含有准多边形铁素体的试样。可见，X80钢屈服强度的降低小于含有针状铁素体或准多边形铁素体的X70钢。

4.2 制管工艺对屈服强度的影响

影响制管前后屈服强度的其他参数包括制管工艺和制管应变（t/D）。当用螺旋焊工艺将展平钢板制成钢管时，在通过数个轧制机组过程中，钢板经受相对均匀和简单的变形，而用具有不同规格轧制机组的电阻焊工艺将展平钢板制成钢管时，钢板经受非均匀且复杂的变形。螺旋管的直径大于电阻焊管，而因不同的制管方向（30°和90°），电阻焊管的t/D较大。S7和E8试样由钢管压平至钢板的屈服强度比展平钢板分别低8 MPa和47 MPa（见表4）。这是因为E8试样在预应变为1%～2%范围内 1stBS突然增加（见图 12（b））。因此，具有相对较大包辛格效应和小的应变硬化效应的钢，制成螺旋管比电阻焊管的屈服强度的降低相对更少一些。但当包申格效应和应变硬化效应同时较大时，制成电阻焊管的屈服强度的变化也是可以接受的。

4.3 估算屈服强度的应用

在制管过程中，展平钢板通常要经受各种变形过程，如拉伸、压缩、弯曲等。一般情况下，单向拉伸－压缩变形代表了包申格效应。因此可以用简单的弯曲来估算沿圆周方向的制管过程，测量和估算的钢管屈服强度之间的差异很小（最大4.7%）。这就意味着这种情况下可以不考虑双向拉伸－压缩变形或剪切变形。

本研究中通过制管和压平过程的拉伸－压缩－拉伸或压缩－拉伸－拉伸双循环模拟试验来计算1stBS和2ndBS。制管前后屈服强度的变化可通过比较三个试样的1stBS及分析显微组织来定性的估算，也可结合2ndBS、Swift方程和预应变方程来定量的估算。在这些估算屈服强度的方程中，2ndBS和Swift方程中包含了显微组织因素，预应变方程中包含了制管工艺因素。

测量和估算的屈服强度之间存在小差异的原因与本估算方法有关：①虽然认为对数坐标中包申格应力参数与预应变成线性比例关系，但不是完全的比例关系；②流动曲线与Swift方程很好地吻合，但两者之间还是有些差异；③由复杂的电阻焊制管工艺制成的E8试样比由相对简单的螺旋焊制管工艺制成的S7和S8试样误差范围大些。这是因为电阻焊管沿切线方向的流动性能可能不均匀。

这些原因造成测量和估算的屈服强度不同，但本研究中提出的估算方法可应用于不同的结构材料以及管线钢制管过程中，具有重复拉伸和压缩应变的变形过程。

4.4 估算屈服强度的优缺点

4.4.1 估算方法的局限性

（1）在拉伸和压缩试验过程中，测试材料的拉伸和压缩变形行为必须相同。但实际材料，如钢、钛合金、金属基复合等材料中存在拉压强度差（SD）效应。在目前的X70和X80钢中，因在非奥氏体再结晶区域内很难形成马氏体，且经高轧制压下率（80%以上）轧制，晶粒被细化，残余应力和晶粒可能不会产生方向性。因此，目前的X70和X80钢的拉伸和压缩屈服强度是相同的，且流动应力在不超过10 MPa的误差范围内几乎是相同的（见图 10（c））。

（2）在不同的预应变下，反向流动曲线一定近乎相同。在某些孪晶诱导塑性（TWIP）钢和双相钢中，反向流动曲线并不总是相同的。在某些相变诱导塑性（TRIP）辅助的双相钢中，由于消除应力而使包申格效应几乎可以忽略不计，反向屈服强度随着预应变的增加而增加。在这些情况下，因为不能用Swift方程公式化，因此不能使用该估算方法。另一方面，因反向流动曲线总是相同的，本研究中的管线钢可用Swift方程公式化。因SD效应很小且反向流动曲线可用一条曲线表示，因此管线钢的屈服强度可用提出的估算方法来有效地估算。

4.4.2 估算方法的优势

（1）X70和X80管线钢板在制管和压平后的屈服强度可用展平钢板的拉伸/压缩性能进行估算，并可在展平钢板的基础上预测钢管屈服强度的变化。

（2）应变硬化效应和包申格效应可通过制管和压平过程的双循环模拟试验进行评估，从而可开发出提高应变硬化效应、并使包申格效应最小化的有效方法。

（3）因包申格应力参数、Swift方程和预应变方程中均包含显微组织因素和制管因素，因此，不需要再额外考虑其影响。

4.4.3 估算方法的缺点

（1）因电阻焊管的工艺比螺旋管复杂，因此电阻焊管中可能会出现问题。

（2）对于经常会产生SD效应且反向流动曲线不能形式化的TRIP和双相钢等材料，使用该估算方法有局限性。

5 结 论

（1）准多边形铁素体、针状铁素体和马氏体－奥氏体组分的体积分数是影响制管前后屈服强度的主要显微组织参数。含有针状铁素体和马氏体－奥氏体组分的钢使屈服强度的降低达到最小，因为其应变硬化效应大于含有准多边形铁素体的钢，而包申格效应变化不大。

（2）制管工艺和制管应变（t/D）是影响屈服强度的重要制造参数。在具有大的包申格效应和小的应变硬化效应的钢中，螺旋管较电阻焊管具有使屈服强度的降低达到最小的优点。当包申格效应和应变硬化效应两者都很大时，甚至电阻焊管都可能大大阻止屈服强度的降低。

（3）双循环模拟试验结果表明，Swift方程和包申格应力参数相结合可估算管子外壁或内壁的屈服强度。这些估算的屈服强度与测量的由管子压平钢板的屈服强度吻合很好，误差不超过4.7%。

（4）利用展平钢板的拉伸/压缩性能可预先估算制管前后屈服强度的变化，因为拉压强度差效应很小，且反向流动曲线可由一条曲线表示。因此，目前的估算方法对控制显微组织和制造工艺参数以使管线钢钢板屈服强度的降低达到最小起到了重要作用。

译自：SOHN S S，HAN S Y,SANG Y S,et al.Analysis and estimation of the yield strength of API X70 and X80 linepipe steels by double-cycle simulation tests[J].Metals and Materials International，2013，19（3）：377-388.

Analysis and Estimation of the Yield Strength of API X70 and X80 Linepipe Steels by Double-cycle Simulation Tests

Edited and Translated by FANG Wei， LYU Hua， XU Ting， XU Xiaofeng
（CNPC Tubular Goods Research Institute,Xi’an 710077,China）

TG142.1

A

10.19291/j.cnki.1001-3938.2017.01.012

2016-10-16

编辑：汪翰云

质检公益性行业科研专项经费资助项目“桥梁缆索用钢等23项国际标准研制——石油天然气工业油气井套管或油管用钢管等5项国际标准研制”（项目号201510205-03）。

方 伟（1968—），女，高级工程师，硕士，主要从事石油管材的标准化工作。