一种新型二维条码的生成和识读

廖景辉，楼喜中

(中国计量大学 信息工程学院，浙江 杭州 310018)

一种新型二维条码的生成和识读

廖景辉，楼喜中

(中国计量大学 信息工程学院，浙江 杭州 310018)

提出了一种新型的二维码编码和译码方案，基于Turbo码的编码和软译码方法，对二维条码进行改进，使其具有更强的识读能力.使用(13，15)的Turbo码编码器和矩阵交织器对源信息流进行编码得到一组二进制流，对编码得到的二进制流进行图像生成得到新型的二维条码.对使用后的二维条码图片进行图像采集，然后进行灰度量化得到软比特信息流，对软比特信息流使用矩阵解交织器和Turbo码译码器进行译码得到源信息流.通过这样的方法可以提高二维条码图片的可识别性.运用这种新型的二维条码图片在工业零部件和军事零部件上，可减少因二维条码无法识别产生的经济损失.

二维码；Turbo编码；Turbo译码

Abstract: A novel encode and decode project, which improves the readability of the two-dimensional bar code, was proposed based on Turbo. A Turbo encoder and a matrix interleaver were used to encode the source information to get a set of binary streams. The new two-dimensional bar code picture was procuced by using the algorithm of picture encoding. The image of the used pictures was processed with the algorithm of grey level quantization to get soft-bit information stream information. The soft-bit information stream was decoded by using a matrix deinterleaver and a Turbo soft decoder to get the source information. This method improved the recognizability of two-dimensional bar code pictures. The application of the two-dimensional bar code pictures to the industry and military can reduce economic losses.

Keywords: two dimensional bar code; Turbo encode; Turbo decode

全球现有的二维码中，最常见的有QRCode二维码、PDF417二维码、DataMatrix二维码等几十种.在日常百姓的生活当中最常见的是由日本Denso-Wave公司在1994年所发明的QRCode二维码[1]，QR来自英文Quick Response的缩写，即快速反应的意思，其高速的识别能力有区别与其他二维码.运用特定的数据压缩来表示汉字，只需要13比特就可以表示一个汉字，而其他二维码因为没有特定的汉字模式因此需要16比特才能表示一个汉字，效率相对其他二维码提高了20%，并且QRCode码可以存储4 296个字母数据或者7 089个数字数据，相比于其他二维码可以存储更多的字母、数字、字符.

工业当中最常见使用的是由RVSI Acuity Cimatrix发明的DataMatrix[2]的二维码，相对于QRCode二维码，DataMatrix二维码密集度高，应用简单，易被普通摄像头识别，且更加安全，纠错能力约为33%，相比QRCode码最大纠错能力不超过30%略高，因此只需要读取一定量的资料即可精确读取出信息.

二维码识别是通过使用图像采集设备对黑白色块的辨识和对二维码的纠错将二维码中所携带的源数据信息流读取出来.现有的二维码利用计算机内部逻辑基础的“0”、“1”比特流的概念，使用的是深色表示“1”比特、浅色表示“0”比特.各个二维码具有一定的纠错能力，因此当二维码图片有部分污染、破损、褶皱时仍可识别出源数据信息流.当二维码被大规模污染、破损、褶皱时，扫描设备无法通过识别二维码进行纠错从而获得源数据信息流.

为了提高二维码的可识读能力，本文在编码方面运用由Turbo码编码器和矩阵交织器，将源数据信息流通过Turbo码编码器和矩阵交织器在满足ECC200表格规则后得到二维码图片.在译码方面，对二维码图片进行灰度量化得到软比特信息，对软比特信息运用矩阵解交织技术和Turbo译码器得到源数据信息流.运用交织技术将因为污染破损褶皱而产生的突发错误变成随机错误；运用Turbo译码器可更好的识别出二维码图片中所携带的比特信息.将通过这种编码得到的二维码图片用于工业零部件、军事零部件，由于识别率提高因而可以更广泛地运用于激光雕刻在零部件上.这种二维码图片不仅可以使用更长的时间，而且可以减少因污染、破损、褶皱而导致无法识别二维码.在越来越多的场合，比如汽车工业领域，零部件的更新和维修需要及时追溯零件产生和使用过程的记录信息，二维码可以唯一确定零部件的信息，配合系统软件的使用，可以知道零部件的日常维护和维修记录，从而更好地对零部件进行管理.

现有的二维码一般使用的是Reed-Solomon[3]算法，Reed-Solomon译码算法基于求解线性方程组来对输入编码进行纠错.如果二维码译码选用可以软信息输出的Turbo译码算法，通过给出译码结果的软信息输出值并将这个值作为外部信息传递给下级译码器从而得到最大似然序列，实现过程相对简单.通过计算每个色块黑白占有比率直接输出占有比率，可以更加准确地分析和读出二维码当中的源数据信息流，从而提高了译码性能，增强了二维码可识别能力.

1 一种新型二维码编码方法

将源数据信息流通过转换成8位源数据二进制流输入到递归系统卷积码编码器和矩阵交织器最终转换为二维码图片，具体步骤如下.

步骤一：将源数据信息流通过查询ASCII码表转换成对应的8位二进制流，将二进制流通过Turbo编码器计算得到二进制流的个数，将计算所得到的二进制流的个数与ECC200表格规则中由数据区域预设规定所需要输入的二进制流个数相比较，来判断源数据信息流是否满足ECC200表格规则，将二维码图像填充完整.

步骤二：如果源数据信息流满足ECC200表格规则，则将源数据信息流根据查询ASCII码表生成8位在(0,255)范围内的长度为K源数据二进制流XK.为了将寄存器在编码后归零，含有递归系统卷积码(RSC)编码器[4]会根据编码器中反馈结构在后面添加3个尾比特使编码器状态W归零.将源数据二进制流通过Turbo编码器码进行编码，编码器结构如图1.

图1 1/2的Turbo编码器Figure 1 1/2 turbo encoder

根据原理图1，它的生成多项式可由公式(1)(2)(3)来表示，其对应的八进制形式为(1,13/15)，书写方便，通常都记为(13,15).

(1)

g1(D)=1+D+D3,

(2)

g0(D)=1+D2+D3.

(3)

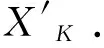
(4)

π(i)=(f1i+f2i2)modK.

(5)

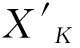
如果源数据信息流不满足ECC200表格规则，那就要根据源数据信息流计算满足ECC200数据区域表格规则所需要补充的二进制流，同时将源数据信息流根据查询ASCII码表生成8位在(0,255)范围内源数据二进制流{xi}根据ECC200表格规则中由数据区域预设规定所需要转换的二进制码个数与源数据二进制流个数进行比较，计算符合ECC200表格规则原本需要输入的源数据二进制流与源数据信息流转换成的源数据二进制流的差值个数a，在源数据二进制流后补充差值个数为a的“0”比特，得到新的源数据二进制比特流XK，将源数据二进制流XK进行编码得到数据码字.

步骤三：将步骤二中的数据码字输入到矩阵交织器[7]中进行交织，其交织器首先对数据码字进行分组交织，将列数C预设为30，然后设数据码字的码字个数为U，找出满足不等式U≤RC的最小整数R，得到行数R.确定行数R后，得到矩阵A，接下来将数据码字逐行写入矩阵A中，若数据码字无法将R行写入完整，则用数据二进制流的0或1将R行其它空缺位置填补，将矩阵A进行矩阵变换得到新矩阵B，如矩阵A按照表1进行变换，最终将新矩阵B逐列读出数据，并将之前不存在数据码字中的数据二进制流的0或1去掉，得到最终码字.见表1.

表1 编码交织器列排序

步骤四：将最终码字按照输出的排列顺序从左到右、从上到下分别填充到二维码数据区域.在已填充好的数据区域外加上取景器实心“L”型边界和黑白交替的反“L”型虚线边界，从而能够得到可供识别的二维码.

2 二维码译码方法

用能够识别新型二维码的扫描器扫描二维码，通过特定的图像处理获取二维码的软信息序列，将获取得到的二维码软信息序列通过译码器译码得到源数据信息流，所述译码器由解调器、矩阵解交织译码器和维特比软判决译码器构成，具体的步骤如下.

步骤一：使用能够识别新型二维码的扫描器对二维码进行扫描，通过特定的图像预处理采集二维码图像.

步骤二：对采集的二维码图像进行灰度化.

步骤三：对灰度化的图像进行二值化.

步骤四：获得图像大概区域，对图像进行粗定位.

步骤五：检测DataMatrix二维码的“L”型边界.

步骤六：计算图像倾斜角度.

步骤七：根据倾斜角度对图像进行旋转.

步骤八：对旋转后的二维码图像进行矫正处理.

步骤九：对矫正处理后的二维码图像进行偏差处理.

步骤十：对偏差处理过后的二维码图像输出，生成标准二维码矩阵.

步骤十一：对生成的标准二维码矩阵通过解调器运用软判决方法解调得到软信息比特流.

步骤十二：将解调得到的软信息比特流进入矩阵解交织译码器进行解交织得到一组新的软信息比特流，其矩阵解交织译码器具体算法是会构造一个解交织矩阵，其中规定解交织矩阵列数C为30，根据接收到的码字，设码字个数为U′，找出满足不等式U′≤CR′中的最小整数R′，得到行数R′，确定行数R′后，得到矩阵D，将接收到的码字逐列写入矩阵D中，若输入码字无法将行数R′写入完整，则用数据二进制流的0或1将行数R′其它空缺位置填补，然后将矩阵D经过矩阵变换，矩阵D按照表2进行变换，从而得到新矩阵E，接下来将矩阵E逐行读取，并将之前不存在数据码字中的数据二进制流0或1去掉，得到解交织后的软信息比特流.

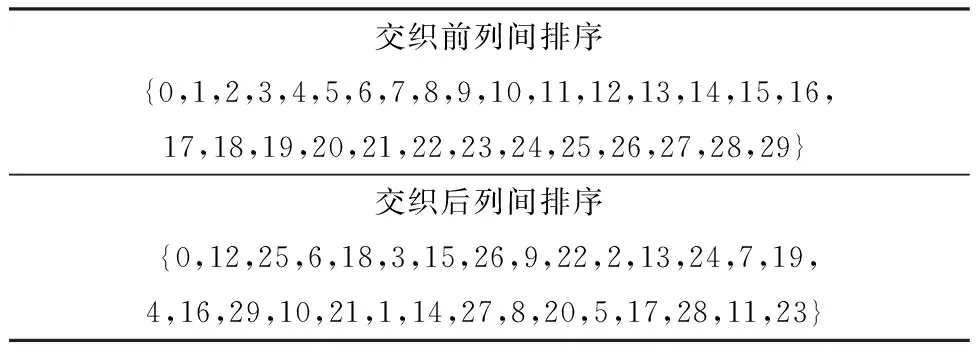
表2 译码交织列排序

步骤十三：将解交织后的软信息比特流输入到由两个软输入软输出(SISO)构成的串行级联Turbo码译码器DEC1和DEC2[8]，译码器DEC1对分量码RSC1进行最大似然译码，产生关于源数据二进制流XK中每一个比特的似然比信息，并将其中的“外部信息”经过交织送给DEC2，译码器DEC2将此信息作为先验信息，对分量码RSC2进行最佳译码，产生交织后源数据二进制流中每一比特的似然比信息，然后将其中的“外部信息”经过解交织后送给DEC1，进行下一次解码.经过多次迭代后，DEC1或DEC2的外部信息趋于稳定，似然比渐进值逼近于对整个码的最大似然估计译码，对此似然比进行硬判决即可得到最佳估值序列.

步骤十四：根据最佳估值序列还原得到源数据二进制流.

步骤十五：根据还原得到的源数据二进制流解析出源数据信息流.

在此基础上再引导学生仿写练习，学生就知道可以从颜色、形状、数量、神态等方面去写好事物或人物，要结合事物特点去修饰，而不是一味照抄却不知道抄的是什么，也不会张冠李戴，把“慈善的目光”用来形容小妹妹了。

3 实 验

以码率为1/2的Turbo码为例，输入三个源数据信息流，源数据信息流转换成八位二进制码，从而得到24位二进制码，根据Turbo编码器得到54位二进制码，根据得到的二进制码选择ECC200数据区域为8×8的表格，即源数据信息流不满足ECC200表格规则，因此需要补充5个“0”比特到源数据二进制流XK，从而编码得到64位二进制码以满足ECC200表格规则[9].

例如输入“ABC”两个字符，查询ASCII表格得到二进制流{01000001

01000010

01000011}，根据Turbo编码器要求得到54位二进制码，在添加5个“0”比特后重新对源数据二进制流XK编码得到{001001000101001001110

1000100100101100101011

011000001000000111011}，根据交织矩阵列变换排列规则可得到矩阵B

{001001000101001001110100010010

010110010101101100000100000011并且

101100000000000000000000000000}按列读出并去掉补充的二进制流0或1得到最终码字{001000010011001100000

0101101011110000000111

001011010110101000010}，根据二维码转换规则得到满足ECC200表格规则的可识别的二维码如图2.

图2 源数据信息流ABC的二维码Figure 2 Two-dimensional bar code of source data stream ABC

4 实验结果

通过对不同的源数据信息流进行编码，可以快速得到满足不同字符要求的可识别二维码图片.利用MATLAB软件对Turbo码在加性高斯白噪声信道环境下进行仿真，系统采用的是BPSK调制方式，长度为1 024.

对LOG-MAP算法、SOVA算法、MAX-LOG-MAP算法在AWGN信道中进行仿真比较[10]，RSC子码的生成多项式为(13,15)，系统码率为1/2，译码迭代3次，结果如图3所示.仿真结果表明，在这三种算法中，LOG-MAP算法表现最好，MAX-LOG-MAP算法表现次之，之后是SOVA算法.在高信噪比时，SOVA性能下降十分明显.从算法复杂度而言，LOG-MAP算法最为复杂，之后是MAX-LOP-MAP算法，SOVA算法最简单.因此可以得到性能优异的Turbo译码算法是以牺牲算法的简易性为代价.

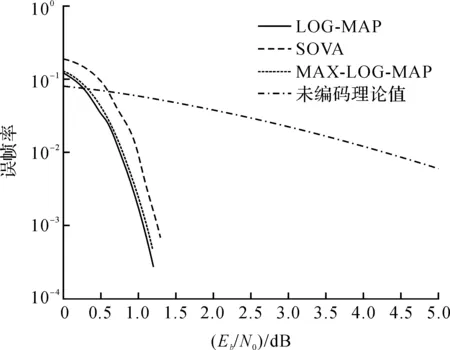
图3 Turbo码不同算法性能AWGN信道测试Figure 3 Different algorithm decoding performance in AWGN channel of turbo code

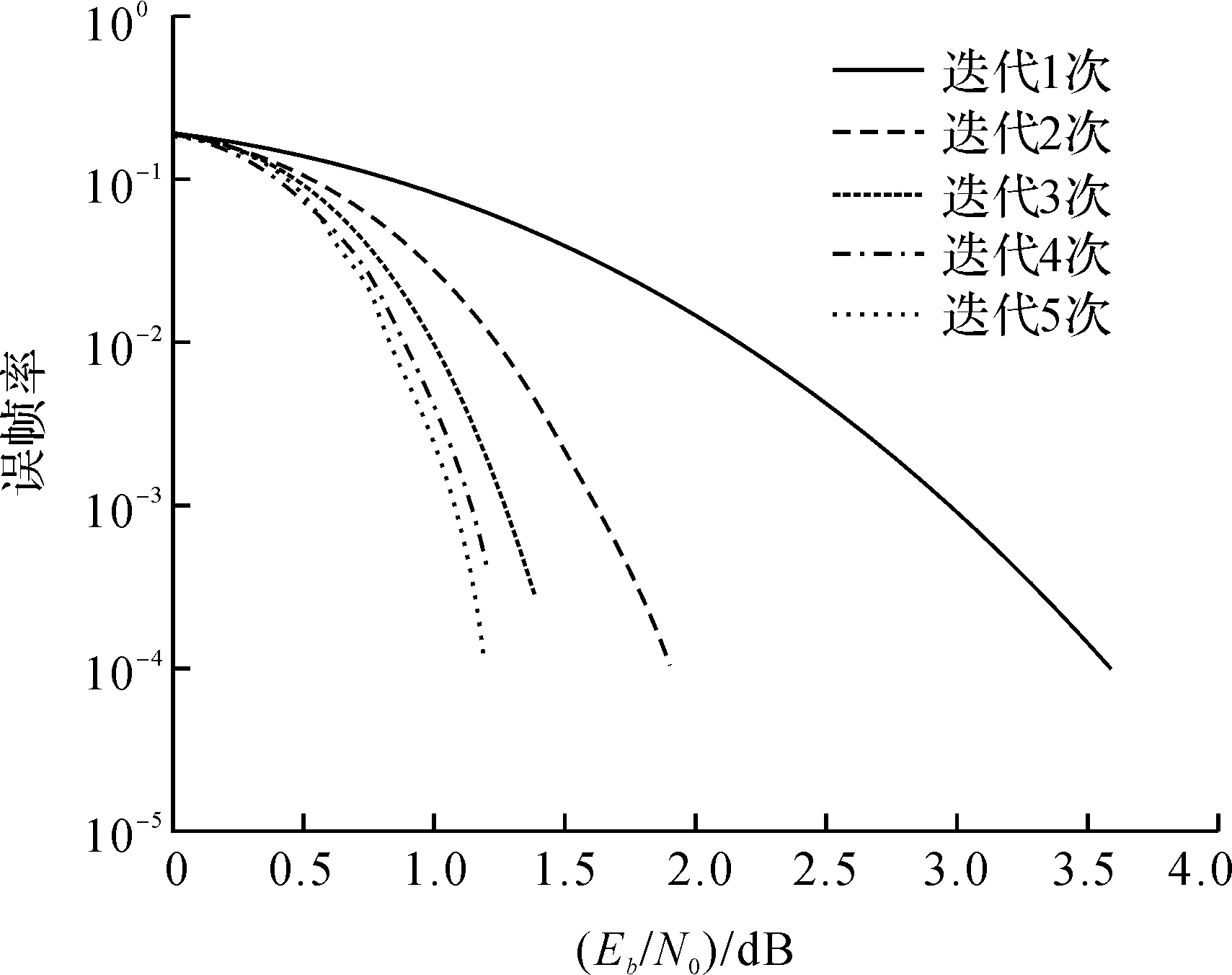
图4 Turbo码不同迭代次数译码性能AWGN信道测试Figure 4 Different iteration number decoding performance in AWGN channel of turbo code

对于不同的迭代次数，使用SOVA算法[11]，并且通过AWGN信道进行仿真比较，RSC子码的生成多项式为(13,15)，系统码率为1/2，结果如图4所示.仿真结果表明，第一次迭代的误比特性能较差，因为两个分量译码器之间的外部信息没有很好的互相利用，随着迭代次数的增加，两个分量译码器之间的外部信息得到更好的利用，似然比渐进值逼近于最大似然估计译码，解析得到源数据信息流的可能性也就越大.当迭代次数达到一定数值时，译码性能趋于稳定，增加新的迭代对性能的改善非常小并且运行时间显著增加.因此选择合适的迭代次数对二维码的译码效率也尤为重要.

对于不同的约束长度，使用SOVA算法并且通过AWGN信道进行仿真比较，RSC子码的生成多项式为(13,15)，系统码率为1/3，结果如图5所示.仿真结果表明，约束长度越长，Turbo码的纠错能力越好.但约束长度的增加会提高译码的复杂性，因此为了二维码的译码效率需要选择适当的约束长度.

对于不同的码率，使用SOVA算法并且通过AWGN信道进行仿真比较，RSC子码的生成多项式为(13,15)，系统迭代次数为3次，结果如图6所示.仿真结果表明，在达到误帧率10-5时，码率1/3比码率1/2低1.5分贝.说明码率越大，对于信道的纠错能力也就越弱.对于约束度确定的RSC编码器，为了让二维码携带更多的源信息数据需要改变删余矩阵对校验流的删减，增大码率.

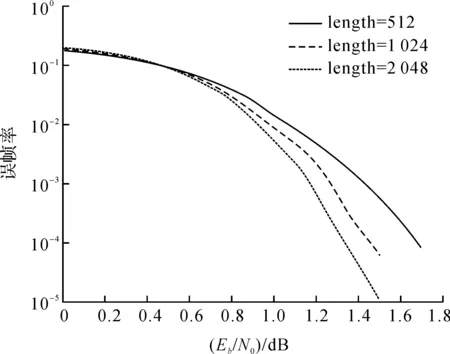
图5 Turbo码不同约束长度性能AWGN信道测试Figure 5 Different constraint length of Turbo code performance in AWGN channel

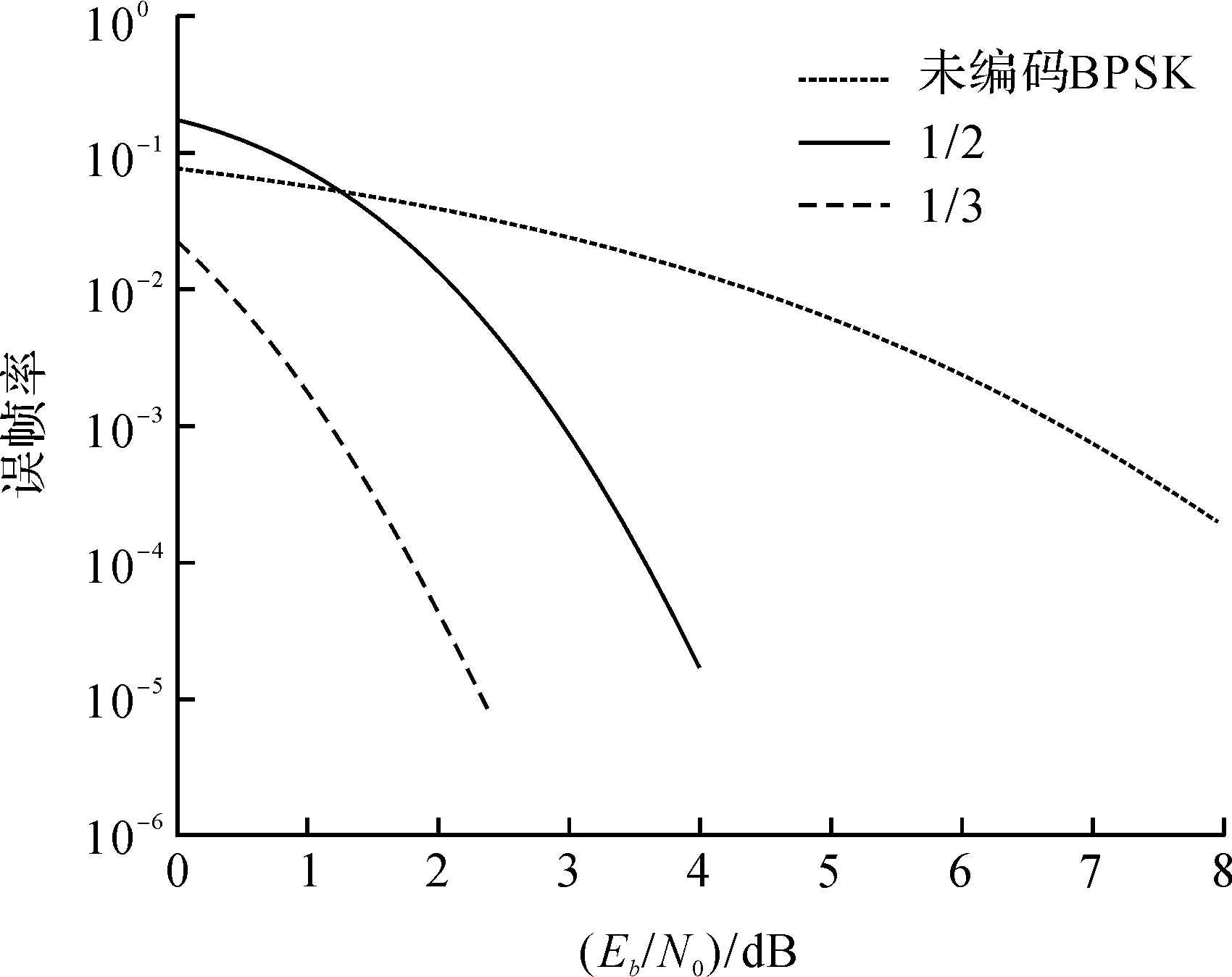
图6 Turbo码不同译码速率性能AWGN信道测试Figure 6 Different decoding speed performance in AWGN channel of turbo code

对于DataMatrix、QRCode等常用的纠错算法Reed-Solomon(基于NASA标准)，运用RS(255,223)与Turbo码进行比较.上述几个比较实验可以确定使用Turbo码的几个参数.在AWGN的信道中编码BPSK性能中，使用RSC子码的生成多项式为(13,15)，系统码率为1/2，系统迭代次数为3次的SOVA译码算法的Turbo码与使用硬判决的RS(255,223)译码相比，在达到误帧率10-5时，Turbo码性能比RS码低4分贝，可以在更低的信噪比下拥有更小的误帧率，仿真结果如图7.

图7 RS码，Turbo码性能AWGN信道测试Figure 7 RS code, Turbo code performance in AWGN channel

5 结 论

本文通过使用基于Turbo编码方法与基于Turbo译码算法和矩阵交织技术对二维码图片进行软译码方法，能够提高二维码的可识别能力和自我纠错能力.为了提高二维码的译码速度选择使用SOVA译码方法，系统迭代次数为3次，约束长度为1 024.根据源数据信息流的长度选择ECC200表格规格，参考表格的纠错率对不同长度的源数据信息流选择不同的译码速率.但Tubro码固有缺点有较大的延时，在低速的二维码中，要求源数据信息流的长度不宜过长.鉴于此问题，我们需要对其中的二维码图片编码和译码方法做进一步的改进，以便在实际应用中能够得到更广泛的运用.

[1] 王文豪. QR Code二维条形码的图像识别[J]. 计算机技术与发展, 2009,19(10): 122-126. WANG W H. Image recognition in 2-D bar code based on QR code[J].ComputerTechnologyandDevelopment, 2009,19(10): 122-126.

[2] 邹沿新,杨高波. Data Matrix二维条形码解码器图像预处理研究[J]. 计算机工程与应用, 2009, 45(34): 183-185. ZOU Y X, YANG G B. Research on image pre-processing for Data Matrix 2D barcode decoder[J].ComputerEngineeringandApplications, 2009, 45(34): 183-185.

[3] DARNELL M. Error control coding:fundamentals and applications[J].IETJournals&Magazines, 1865,132(1): 68-68.

[4] 王秀敏, 洪芳菲, 单良, 等. LDPC/Turbo双模译码器技术发展与前景综述[J]. 中国计量学院学报, 2016, 27(1):63-67. WANG X M, HONG F F, SHAN L, el al. The advance overview on LDPC/Turbo dual-mode decoders[J].JournalofChinaUniversityofMetrology, 2016, 27(1):63-67.

[5] WANG W W, GUAN Y L, YANG P, et al. Turbo equalization for waveforms encoded by reed Solomon codes[C]//MilitaryCommunicationsConference. Tampa：IEEE, 2015:804-808.

[6] 韩新强, 金小萍, 冯会真, 等. 差分协作系统中的软输入软输出多符号差分球形译码[J]. 中国计量学院学报, 2013, 24(2):171-176. HAN X Q, JIN X P, FENG H Z, el al. Soft-input soft-output multiple-symbol differential sphere decoding for differential cooperative system[J].JournalofChinaUniversityofMetrology, 2013, 24(2):171-176.

[7] JEONG J, YOON D, LEE J. Blind reconstruction of a helical scan interleaver[C]//Information,CommuicationsandSignalProcessing(ICICS). Singapore：IEEE, 2011:1-4.

[8] HANGENAUER J, OFFER E, PAPKE P. Iterative decoding of binary block and convolutional codes[J].IEEETransactionsonInformationTheory, 1996, 42(2):429-445.

[9] NAMBUTDEE A, AIRPHAIBOON S. Medical image encryption based on DCT-DWT domain combining 2D-DataMatrix Barcode[C]//20158thBiomedicalEngineeringInternationalConference(BMEICON). Pattaya：IEEE, 2015:1-5.

[10] LING C, CUI L, WU X F. Further results on the equivalence between SOVA and max-log-MAP decodings[C]//CommunicationTechnologyProceedings(WCC-ICCT2000). Beijing：IEEE, 2000:1689-1692.

[11] RAMTEKE S, KAKDE S, SURYAWANSHI Y, el al. Performance analysis of Turbo decoder using soft output viterbi algorithm[C]//CommunicationsandSingalProcessing. Melmaruvathur：IEEE, 2015:1332-1336.

Anoveltwo-dimensionalbarcodegeneratingandreading

LIAO Jinghui,LOU Xizhong

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0365-06

10.3969/j.issn.2096-2835.2017.03.016

2017-07-06 《中国计量大学学报》网址zgjl.cbpt.cnki.net

TN911.2

A

10.3969/j.issn.2096-2835.2017.03.019