基于模糊PID算法的六自由度并联机构控制研究

杨靖一，黄山云，丁祝顺，荆龙宾

(北京航天控制仪器研究所，北京100039）

基于模糊PID算法的六自由度并联机构控制研究

杨靖一，黄山云，丁祝顺，荆龙宾

(北京航天控制仪器研究所，北京100039）

针对六自由度并联机构难以实现高精度及快速响应的问题，分析六自由度并联机构模型，提出基于模糊PID的六自由度并联机构的控制算法。介绍了六自由度并联机构的运动学反解模型及机械系统模型；在此基础上确定模糊算法的模糊语言变量、隶属函数和模糊规则，完成了六自由度并联机构模糊PID控制器的设计。针对一组PID控制参数进行了仿真和实验，结果表明，加入模糊算法的PID控制提高了系统的动态响应特性及运动精度。

运动学反解；模糊PID控制；六自由度；SimMechanics

Abstract：Due to the difficulties in the high precision and fast response of parallel mechanism，the parallel mecha⁃nism model is analyzed，the PID controller based on fuzzy algorithm is proposed to solve the motioned problem.Firstly，the inverse kinematics solution process of parallel mechanism is deduced.On the basis of analyzing the PID control and fuzzy control principle，the fuzzy language variables，membership function and fuzzy rules are determined，then six DOF parallel mechanism fuzzy PID controller is designed to improve the precision and response of the system.Finally，by the simulation and experiment analysis，the results show that the fuzzy PID controller improves the dynamic response performance and pre⁃cision.

Key words：inverse kinematics;PID fuzzy control;six⁃DOF;SimMechanics

0 引言

六自由度并联机构基于Stewart平台原理，由Stewart于1965年在 《A Platform with Six Degree》中首次提出，应用于飞行模拟器的运动研究。近年来，六自由度并联机构以刚度大、结构稳定、承载能力强、精度高、动态性能好等优点成为机器人领域的一个研究热点，已在并联机器人、新型机床、大型射电望远镜、飞行模拟器、航空宇航对接器等领域获得了广泛应用。

六自由度并联机构系统是一个多输入、多输出的复杂非线性系统，具有时变、强耦合和非线性等动力学特点，这给机构的控制研究带来了很大的困难。在六自由度并联机构的运动过程中，平台的姿态变化反解出各杆的期望位移各不相同，甚至相差很大。而传统控制方法一旦控制参数确定，在运动过程中就无法实时调整控制参数，所以传统控制方法无法满足系统在不同位姿情况下快速响应和高精度的要求。文献[1]基于H∞鲁棒控制，提出了一种并联机构鲁棒自适应控制，但其终究还是先进行线性化再进行设计的一种方法，无法完全适应六自由度并联机构非线性控制的要求。文献[2]提出了一种新型滑膜控制算法，其缺陷是控制器频繁切换动作有可能造成跟踪误差在零点附近产生抖动的现象，而不能收敛到零。在此基础上本文首先建立了六自由并联机构模型，针对模型特性设计模糊PID控制器，并对其进行仿真及试验研究，验证了模糊PID在六自由度并联机构控制上的优势，达到了提高机构响应速度及精度的目的。

1 系统描述

六自由度并联机构系统总体框图如图1所示，主要由运动学反解、控制系统和六自由并联机构组成。运动学反解将输入的期望位姿解算为六自由度并联机构6根支腿的目标长度，同时根据反馈得到各支腿的实时长度，计算出各支腿的目标位移。将目标位移和目标位移的微分同时输入控制系统，控制系统根据输入量实时调整控制参数，输出控制信号控制电机驱动，通过对6根电动推杆的控制使六自由度并联机构输出指定位姿。

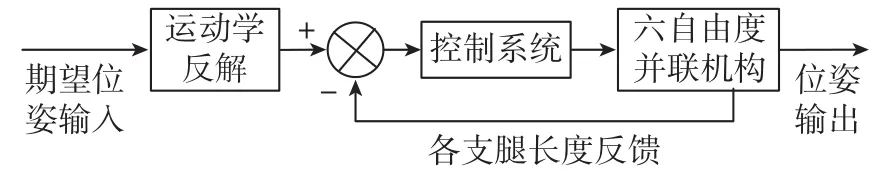
图1 系统总体框图Fig.1 Block diagram of system

下面将对系统运动学反解、控制系统的设计和六自由度并联机构的建模进行详细介绍。

2 系统建模

2.1 运动学反解

并联机构运动学中有两个基本问题，即机构的正解、反解问题。若己知机构主动件的位置，求解机构输出件的位置和姿态，称之为机构位置的正解；若已知输出件的位置和姿态，求解机构输入件的位置，称之为机构位置的反解。由于正解的复杂性，以及无法获得准确解，目前大部分并联机构都采用反解的方法来求解运动学方程。

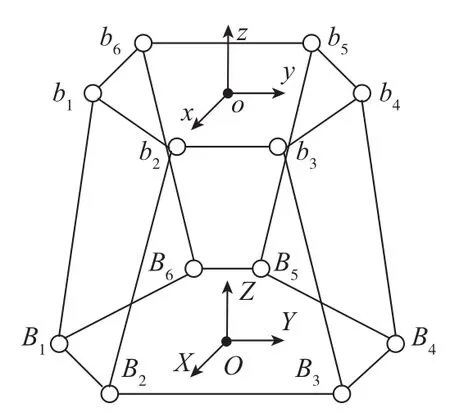
图2 Stewart机构的运动学模型Fig.2 Dynamitic model of Stewart organization institution

图2为Stewart机构的运动学简化模型，固定坐标系O⁃XYZ建立在固定平台上，动坐标系o⁃xyz建立在动平台上，跟随动平台一起运动。建立固定坐标系和动坐标系两者几何矢量关系：

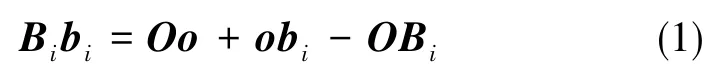
式中，Bi和bi是第i根支链的下固定铰点和上运动铰点。

并联机构的运动逆解是从工作坐标反求铰点坐标，并且有唯一解。位置逆解分析是利用坐标变换，将obi从动坐标系转换到固定坐标系中，求Obi。动平台在固定坐标系中有位置和姿态两个参数，位置是动平台的中心的位置(x，y，z）。姿态为动平台的角姿态，设动平台绕z轴旋转的角为γ，绕y轴旋转的角为β，绕x轴旋转的角为α。

角位移γ、β、α对应的转换矩阵R分别为［3］：

动平台的姿态在空间上可以看到分别绕z轴、y轴、x轴旋转得到，则：

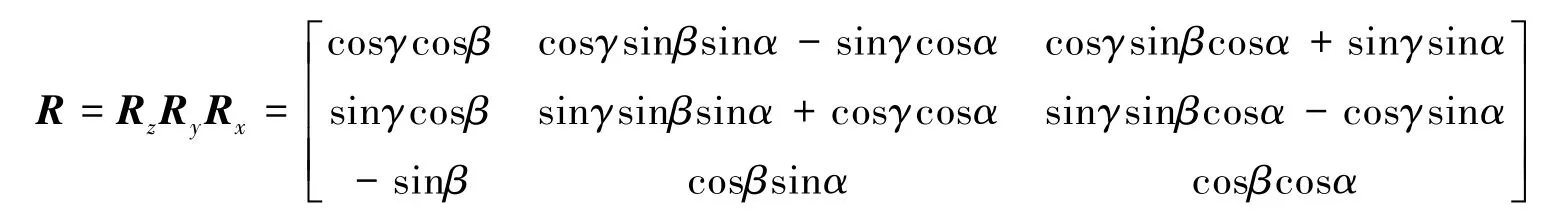
令Obi为Pi，obi为Pi′，Bibi为li，OBi为Bi，Oo为X，则［4⁃5］：

将式(2）代入式(1），得：

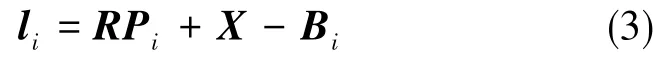
式中，li＝［lixliyliz］T。

则支链i对应的上下铰点间的长度为：

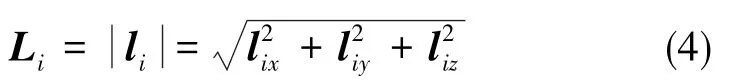
利用式(3）和式(4），即可通过输出件的目标位姿，求解出机构的输入量。

2.2 电动推杆建模

六自由度平台系统的直流电动推杆不同于直流电机，它是通过输入的电压量U(t）转换成距离量X(t），在此过程中电动推杆需要将U(t）逐步转化为电流量I(t）、转矩量T(t）、角速度量Ω(t）和最终的距离量X(t）。对于平台位姿的控制实际需要从控制单个电动推杆开始，因此对于整个电动推杆的模型搭建和计算就显得十分重要。图3是本文所用的电动推杆经过拉普拉斯变换后的传递函数图。

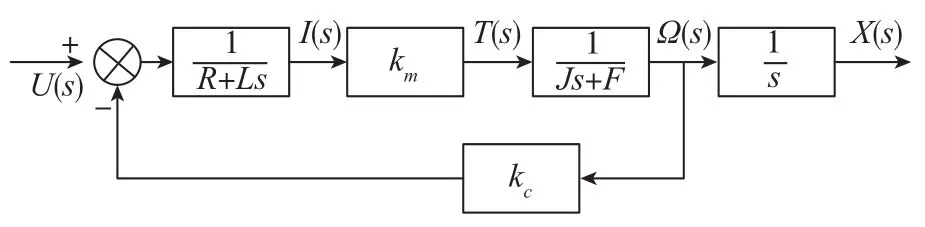
图3 直流电动推杆传递函数图Fig.3 Transfer function diagram of DC electric push rod

通过图3可以得出输入和输出参数之间的关系：

式(5）中，R和L分别代表直流电机的电枢电阻和电感，km是电子转矩和电枢电流之间的系数，J和F是拖动系统整体转动惯量和摩擦转矩，kc是电动推杆的反电动势系数。

2.3 并联机构的SimMechanics建模

目前，对六自由度并联机构的仿真大部分使用的是ADAMS，或者是ADAMS同Matlab的联合仿真，因涉及不同软件的接口问题，数据交换比较复杂。本文利用Simulink中的SimMechanics来构建物理模型，SimMechanics模块库中包含了组成一个完整机械系统所需要的基本模块，利用这些模块可以方便、准确地搭建出机械系统模型［6⁃7］。

六自由度机构结构主要由上、下平台和6根杆组成。其中，上平台由实体库下Body创建，通过参数设置对话框，设置上平台的几何属性、质量属性和初始状态。几何属性包括上平台质心坐标以及同伸缩杆连接点的坐标。固定下平台直接选用Ground模块建模，设定系统环境，包括质量、机械系统维数及分析模式等。定义每根杆的驱动力Fi(i＝1，…，6）为机械系统输入，杆的位移Pi(i＝1，…，6）作为机械系统输出。

六自由度机构伸缩杆由上伸缩杆和下伸缩杆组成，使用实体库、约束库和约束激励库建立模型。在模型中添加伸缩杆同上下平台的接口、上伸缩杆和下伸缩杆、上伸缩杆和上平台的万向副约束、上伸缩杆和下伸缩杆间的圆柱副，同时添加力驱动圆柱副、移动传感器测量伸缩杆的位移、下伸缩杆和下平台间添加万向副约束。最终，建立的模型如图4所示。

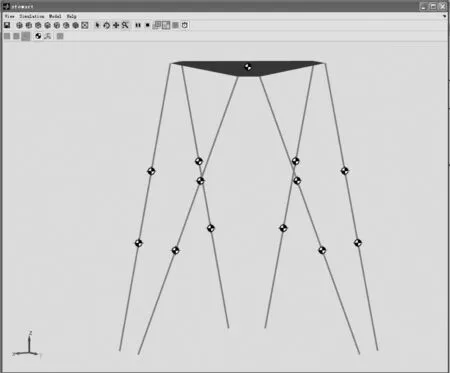
图4 并联机构的SimMechanics模型Fig.4 SimMechanics model of parallel mechanism

3 模糊PID控制器设计

通过以上对模型的分析，可以看出在机构运动过程中不同位姿反解得到的驱动杆的位移各不相同，如果在运动过程中使用同一组不变的控制参数，会对系统的响应速度及精度造成影响。本文提出在PID的基础上，引入模糊控制来改善PID控制在运动过程中不能实时调整参数对六自由度并联机构响应速度及精度带来的影响。

3.1 模糊PID控制算法

六自由度并联机构模糊PID控制器为基于误差驱动的增益调整型控制，由PID控制器和模糊控制器两部分组成。整个模糊PID控制器的结构框图如图5所示。

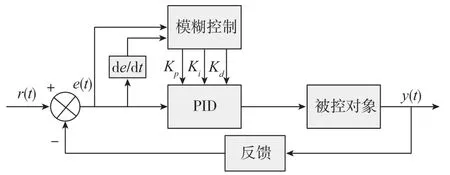
图5 模糊PID控制原理图Fig.5 Schematic diagram of fuzzy PID control

常规PID控制器的算法：

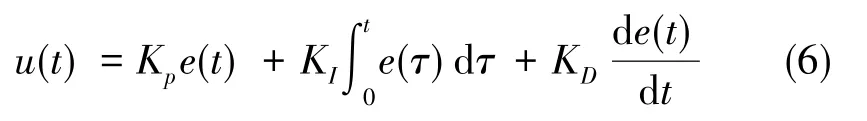
式中，KP为比例控制系数，KI为积分控制系数，KD为微分控制系数，e(t）为期望输入r(t）与实际输出y(t）之间的差值。

模糊控制器主要由4部分组成：模糊化、知识库、模糊推理和清晰化［8⁃10］。

输入输出变量的确定：由于模糊PID控制器主要针对PID的3个参考进行调整，能够实现参数自调整的效果。同时对于该控制器的输入，选用偏差e和偏差变化率 de/dt作为输入，输出为PID 控制的 3 个参数：Δkp、Δki、Δkd。参数kp、ki、kd可由以下公式计算得出：

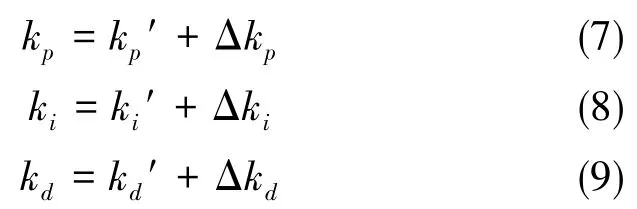
式中，kp′、ki′、kd′均为初始值，即为系统所要改进的传统PID的控制系数。

将输入输出变量所对应的模糊子集以及模糊论域定义为：｛E｝＝｛EC｝＝｛－0.3，－0.2，－0.1，0，0.1，0.2，0.3｝；｛Δkp｝＝｛－30000，－20000，－10000，0，10000，20000，30000｝；｛Δki｝＝｛－300，－200，－100，0，100，200，300｝；｛Δkd｝＝｛－750，－500，－250，0，250，500，750｝。

其中，｛E｝、｛EC｝、｛Δkp｝、｛Δki｝和｛Δkd｝的模糊子集都定义为：｛NB(负大），NM(负中），NS(负小），ZO(零），PS(正小），PM(正中），PB(正大）｝。

模糊规则的确定：根据上文对PID3个参数控制作用的分析，结合专家库中PID控制规则，得出关于Δkp、Δki、Δkd3个参数的控制规则表。如表1所示，文中只给出了Δkp的控制规则，Δki和Δkd的控制规则类似。

表1 ΔKp模糊规则表Table 1 Rule sheet ofΔKpfuzzy

3.2 模糊PID控制器设计

模糊PID是在普通PID基础上，根据经验对控制参数的实时修正，需要先搭建一个PID控制模型，如图6所示。系统输入两个6×1矩阵，pos和r＿pos分别代表传感器观测的6根杆实时位移和经过运动学反解得出的6根杆的目标位移，计算偏差量输入到PID控制器得到一个6×1矩阵Force，即施加在6根杆上的力。其中，kp＝80000、ki＝500、kd＝1800。

由于在并联机构的运动过程中给定目标姿态，经运动学反解得出的各杆目标位移各不相同，所以本文针对6根杆分别设计控制器。6个模糊PID控制器可以根据杆的目标位移与实际位移的偏差量及偏差量变化率实时更新控制参数，达到更好的控制效果。下面以其中1根杆为例设计模糊PID控制器。

在PID控制器基础上引入模糊控制，如图7所示。选择与传统PID的控制参数作为模糊PID控制的初始控制参数，添加Fuzzy Logic Controller模块，分别设置输入输出的论域及模糊规则，选择Max⁃Min的推理算法和面积中心法的清晰化方法。其中，模糊控制器的输入量为目标杆位移和实际杆位移的偏差量，即杆的伸缩量；以及伸缩量的变化率，输出为Δkp、Δki、Δkd，分别和初始控参数kp、ki、kd作和，得到新的控制参数。

图6 PID控制框图Fig.6 The PID control frame

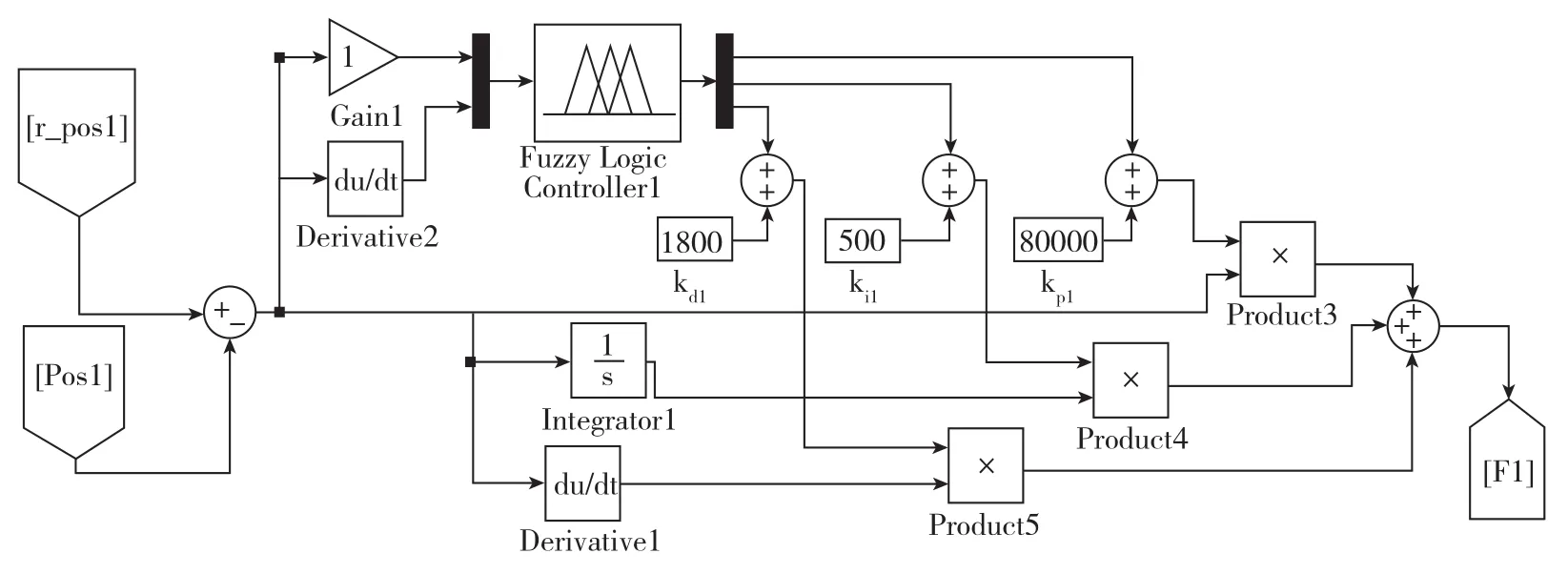
图7 模糊PID控制框图Fig.7 Control frame of fuzzy PID

4 控制系统仿真分析

采用 Matlab/Simulink软件对系统进行仿真，仿真平台的搭建与各模块的连接如图8所示。Leg Trajectory为运动学反解模块，Controller为控制器模块，Plant为机构的机械系统模块。

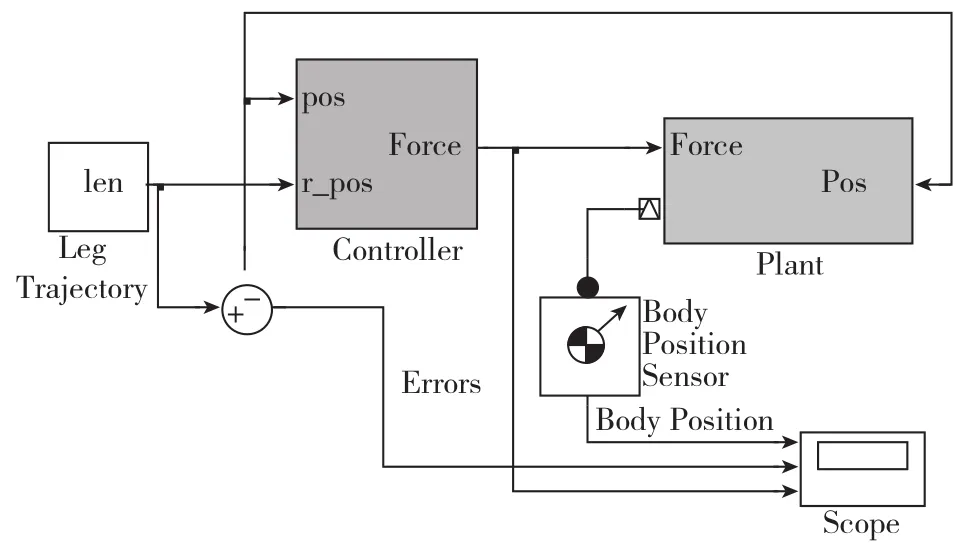
图8 仿真总体框图Fig.8 Overall model of simulation

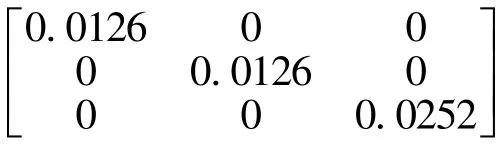
在3个进动方向和3个转动方向分别输入幅值为0.1m和1°、频率为1Hz的正弦信号，针对同一组控制参数分别对传统PID和模糊PID进行仿真，得到曲线如图9所示。

根据仿真结果分析，得到的传统PID仿真及模糊PID的仿真的幅值、误差平均值及误差方差如表2所示。从图9和表2中可以看到，加入模糊算法的PID控制相对传统PID控制在响应速度及精度上都有所改善。

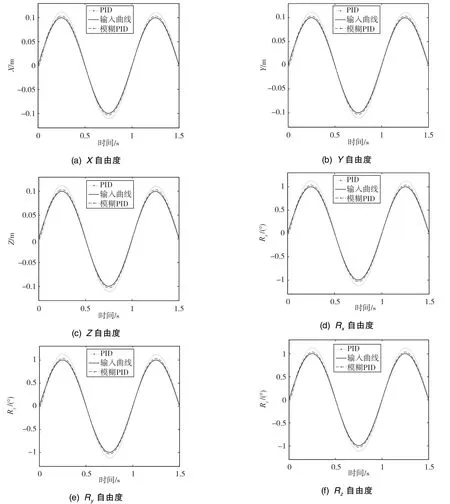
图9 正弦输入输出对比Fig.9 The comparison of sine response

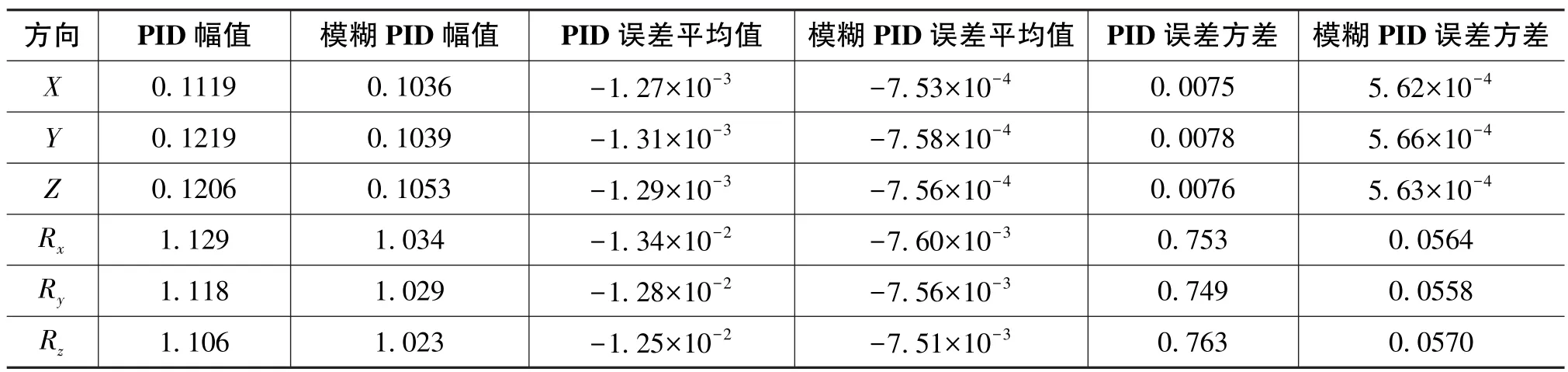
表2 设定信号为1Hz的仿真及实验结果Table 2 Results of simulation and experiment about input signals with frequency of 1Hz

5 实验结果分析

利用实验室现有六自由度并联机构，将模糊PID算法移植到控制板上。由于在各自由度的运动中得到的实验结果类似，这里以绕Y方向的转动为例，输入控制指令使并联机构绕Y轴跟踪幅值为1°、频率为1Hz的正弦曲线转动。利用姿态板采集上平台转动的角度信息，传统PID与模糊PID控制的输出曲线如图10所示。可以看出，模糊PID控制的响应速度及精度优于传统PID控制的响应速度及精度。

图10 正弦输入输出对比Fig.10 The comparison of sine response

传统PID与模糊PID控制的输出曲线与输入曲线作差取绝对值得出误差曲线，如图11所示。模糊PID控制误差均值为0.0597，方差为0.0021。传统PID控制误差均值为0.1348，方差为0.0056。从分析结果可知，在不同位姿情况下模糊PID控制的控制效果相对于传统PID控制的控制效果有所改善。

图11 正弦跟踪误差对比Fig.11 The comparison of sine response error

6 结论

针对六自由度并联机构难以实现高精度及快速响应的问题，本文针对六自由度并联机构特性在传统PID的基础上引入模糊算法，使系统在控制过程中可以实时调整控制参数，建立了并联机构的仿真模型，然后对所建立的并联机构模型进行研究及仿真分析，并在实际的六自由度并联机构中进行验证。结果表明，加入模糊控制的PID改进了传统PID控制在六自由度并联机构中响应速度和精度的不足。

[1]吴东苏.轻型飞行模拟器运动平台先进控制技术研究[D].南京航空航天大学,2007.WU Dong⁃su.Advanced control technology research of light flight simulator motion platform[D].Nanjing University of Aeronautics and Astronautics,2007.

[2]Zhao D Y,Li S Y,Zhu Q M.A new TSMC prototype robust nonlinear task space control of a 6⁃DOF parallel ro⁃botic manipulator[J].International Journal of Control,Au⁃tomation,and Systems,2010,8(6）:1189⁃1197.

[3]陆元九.惯性器件（上册）[M].北京:中国宇航出版社,1993.LU Yuan⁃jiu.Initial devices(1st）[M].Beijing:China Aer⁃ospace Press,1993.

[4]朱晓龙,顿向明.一种五自由度机械臂逆运动学求解的几何法[J].机械与电子,2014,28(5）:77⁃80.ZHU Xiao⁃long,DUN Xiang⁃ming.A geometrical method for inverse kinematics of 5⁃DOF manipulator[J].Machinery＆ Electronics,2014,28(5）:77⁃80.

[5]黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.HUANG Zhen,KONG Ling⁃fu,FANG Yue⁃fa.Theory of mechanism and control of parallel robot[M].Beijing:China Machine Press,1997.

[6]李沛,杨小强,李焕良,等.基于Matlab/SimMechanics的六自由度并联运动平台建模与分析[J].机械与电子,2016,34(3）:75⁃80.LI Pei,YANG Xiao⁃qiang,LI Huan⁃liang,et al.Modeling and analysis of six⁃DOF parallel platform based on Matlab/SimMechanics[J].Machinery ＆ Electronics,2016,34(3）:75⁃80.

[7]张寿凤,袁中凡,李彬彬,等.基于积分分离PID控制的Stewart六自由度台仿真[J].机械科学与技术,2009,28(2）:214⁃217.ZHANG Shou⁃feng,YUAN Zhong⁃fan,LI Bin⁃bin,et al.Simulink of a six⁃DOF Stewart platform integral⁃separated PID control[J].Mechanical Science and Tech⁃nology for Aerospace Engineering,2009,28(2）:214⁃217.

[8]Feng G.An approach to adaptive control of fuzzy dynamic systems[J].IEEE Transactions on Fuzzy Systems,2002,10(2）:268⁃275.

[9]Park K H,Hwang D H,Bien Z.A study on the robustness of a PID⁃type iterative learning controller against initial state error[J].International Journal of Systems Science,1999,30(1）:49⁃59.

[10]陈政文.基于模糊PID控制的退火炉温度控制系统的研究[D].武汉工程大学,2014.CHEN Zheng⁃wen.Annealing furnace temperature control system based on fuzzy PID control[D].Wuhan Institute of Technology,2014.

Research on the Controller of a 6⁃DOF Parallel Platform Based on the Fuzzy PID Strategy

YANG Jing⁃yi,HUANG Shan⁃yun,DING Zhu⁃shun,JING Long⁃bin
(Beijing Institute of Aerospace Control Devices,Beijing 100039）

U666.1

A

1674⁃5558(2017）01⁃01362

10.3969/j.issn.1674⁃5558.2017.05.006

2017⁃01⁃06

杨靖一，男，硕士，导航、制导与控制专业，研究方向为控制。