光学干涉式重力仪的数据处理方法

黄时康，黄腾超

（浙江大学 光电科学与工程学院，浙江 杭州 310013）

光学干涉式重力仪的数据处理方法

黄时康，黄腾超

（浙江大学 光电科学与工程学院，浙江 杭州 310013）

本文研究了光学干涉式重力仪的关键技术中的数据处理部分，阐述了对重力仪测出条纹进行分析处理的两种算法：过零探测法及二阶差分法的原理.并在Matlab平台下针对这两种算法进行了编程仿真，对用两种算法处理同一组数据的仿真结果进行了比较.

光学；干涉；重力仪；过零探测法；二阶差分法

重力场是反映地球内部物质结构及其变迁的地球物理基本场，其主要参数为重力加速度(g，常用值9.81m/s2).g值的精密测量是探测地球重力场的重要途径.重力值测量是计量、测绘、地质、地震与资源勘探等领域不可或缺的部分，其在大地测量、地球物理、精密计量和军用导航等领域具有十分重要的意义和应用价值.

本文的研究内容是第五项关键技术数据处理与仪器控制系统中的数据处理以及误差分析部分.我们根据两种重力值的算法编写程序，利用MATLAB软件对两种算法进行了仿真，对重力仪测量的数据进行处理，计算出了重力值g并进行了比较.

1 数据处理方法

1.1 过零探测法

落体下落距离S（t）的数学模型为：

其中，s0为物体的初始位置，v0为初速度.γ为垂直重力梯度.若重力梯度未知，由于其数值很小（为10-6数量级）则可以忽略不计.

过零探测法的工作原理如下：当物体下落时，重力仪的采点频率为fs=100MHz，如图1所示：

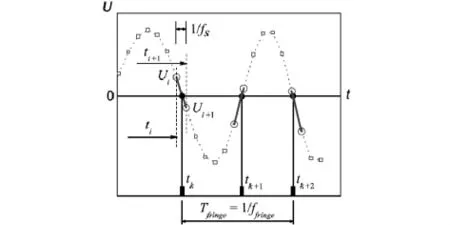
图 1过零探测法原理图

当第i个采样点Ui和下一个采样点Ui+1相乘小于0 时，在Ui与Ui+1之间必定存在一个零点.在Matlab平台下，可以在数秒内完成占存储空间几百Mbite数据量的过零探测.零点的准确时刻tk可由相似三角形关系算出：tk=ti+Ui·Ts/（Ui-Ui+1）.其中，Ts为相邻两点的间隔时间，其值为1/fs，同理，ti=（i-1）/fs.由于两个相邻的零点之间为1/2个条纹周期，其相位变化为π，故物体下落距离为λ/4.所以，在tk时刻物体的位置为Sk(tk)=(k-1)·(λ/4).将Sk(tk)与tk的值代入公式（1.1）中即可求出重力值g

2.2 二阶差分法

二阶差分法的核心思想为，当忽略重力梯度γ的影响时，取固定的Δt，下落距离S（t）的二阶差分Δ2(S(t)=g(Δt)2为常数.

地球的重力值在9.78ms-2至9.83ms-2之间，取 Δt= 0.2ms，则 Δ2在 3.912×10-7m 与 3.932×10-7m之间.测量光源为He-Ne激光器，波长λ=632.8nm.则条纹数差值为Δ2/（λ/2），其数值在1.236与1.242之间.也就是说，将条纹以Δt=0.2ms分为N段，每一段的条纹数Kn会比前一段的条纹数Kn-1多1.236至1.242个.

也就是说，Kn-Kn-1的整数部分是稳定不变的C=1，我们要确定的是小数部分.

图 2二阶差分法原理图

要确定小数部分，只需在每段Δt部分的同一位置取一个点作为特征点，用过零探测的方法求出与该点最近的两个零点，根据该点与前后零点之间点的个数，来求出该点在一个周期条纹中的位置即Φ(n).举个例子，若第n段的特征点是第100个点，距离最近的两个零点是第90个点与第140个点，则Φ(n)=10/50=0.2.将每段的Φ(n)求出后，Φ(n)-Φ(n-1)即为条纹数差Kn-Kn-1的小数部分.

在求出Kn-Kn-1之后，下落距离，之后代入(1.1)中即可计算出重力值g.

2 实验结果分析

下表为通过两种算法计算的重力值（重复实验20次，共20组数据）

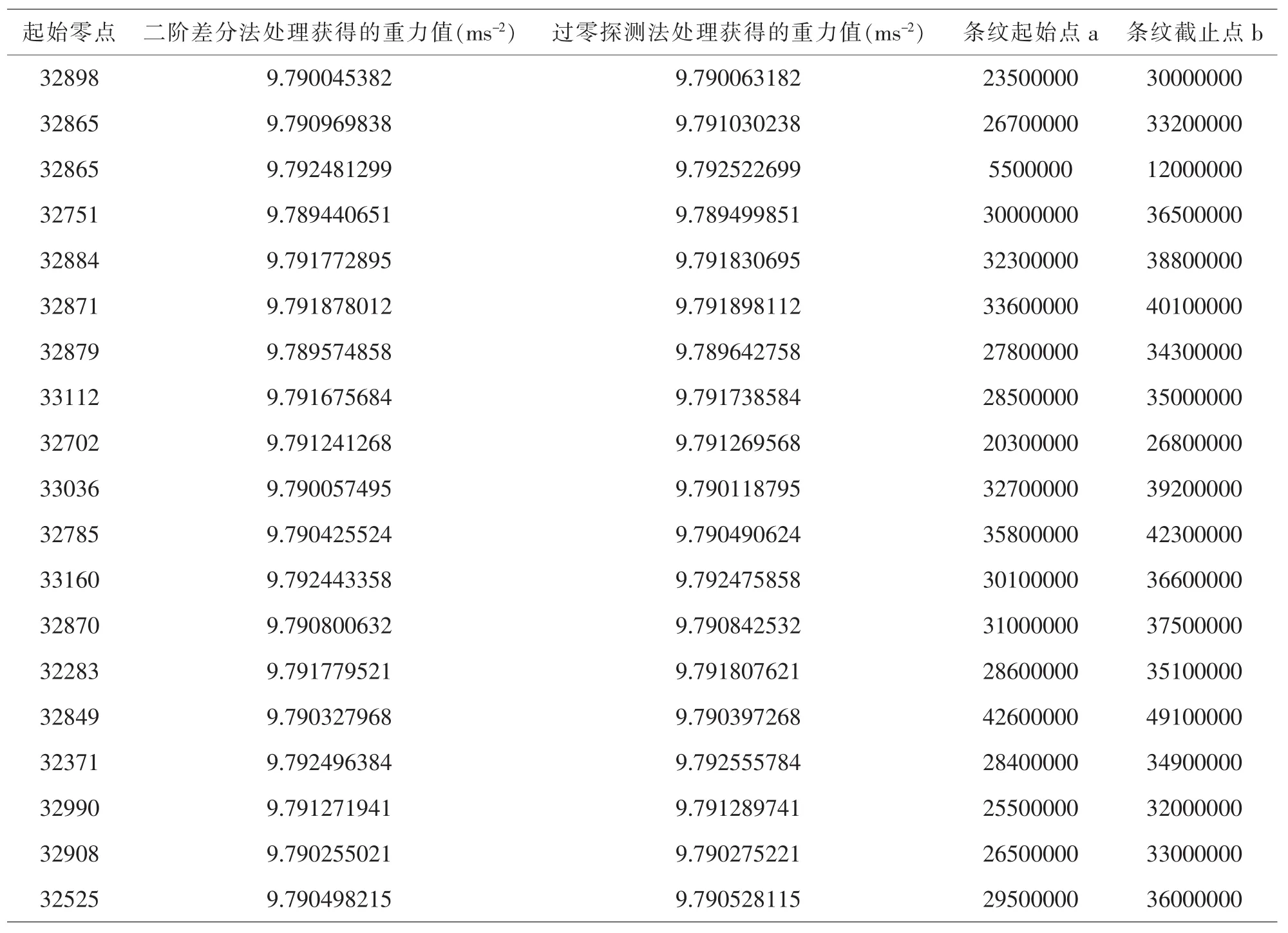
表1 实验数据记录表

对两种方法处理得到的重力值用Matlab画成平滑曲线图.

图3 两种算法计算出的重力值比较示意图

其中，红线代表过零探测法，蓝线代表二阶差分法.从图中可看出，两种算法得出的结果非常接近，几乎没有区别.

过零探测法：

方差：D（g）=8.9428×10-7ms-2

标准差：σ=9.4566×10-4ms-2

二阶差分法：

方差：D（g）=9.0056×10-7ms-2

标准差：σ=9.4898×10-4ms-2

3 结论

本文提出了两种提取重力仪测得的干涉条纹上的信息，计算重力值g的算法（过零探测法与二阶差分法），对误差来源进行了原理分析，并进行了数学建模，计算出了误差的大小.并在Matlab平台下，编写程序，对两种算法进行了仿真计算，并将计算结果进行了比较.结果表明，两种算法的结果几乎一致，但计算结果与真实重力值的差值还待进一步的研究.

〔1〕吴琼.高精度绝对重力仪关键技术研究[D].中国地震局地球物理研究所,2011.

〔2〕Dr.Eberhard Bansch，Lijun Wang,Ph.D，Dr.Thomas Fauster.Ultra-high Precision,Absolute，Earth Gravity Measurements，26. Juni 2008.

〔3〕S Svitlov1,P Mas?yk,Ch Rothleitner,H Hu and L J Wang.Comparison of three digital fringe signal processing methods in a ballistic free-fall absolute gravimeter，11 November 2010.

〔4〕高景龙.NIM-3型新的轻小高精度可移式绝对重力仪[J].测绘学报，1993，22（3）.

〔5〕郭有光，黄大伦，方永源，徐进义，刘达伦.中国NIM型绝对重力仪及国际绝对重力仪比对[J].现代计量测试,1998（6）.

〔6〕W.TORGE,R.H.RDER,M.SCHNIJ LL,H.-G.WENZEL.FIRSTRESULTSWITH THE TRANSPORTABLE ABSOLUTE GRAVITY METER JILAG-3,1987.

〔7〕T M.Niebauel;G.S.Sasagawa,J.E.Fallel;R.Hilt and E Klopping，A new generation of absolute gravimeters，1995.

〔8〕J.Liard and C.Gagnon.The new A-10 absolute gravimeter at the 2001International Comparison of Absolute Gravimeters.2002.

〔9〕Giancarlo D’Agostino,Sergio Desogus,A-lessandro Germak, Claudio Origlia, Danilo Quagliotti,Giovanna Berrino,Gennaro Corrado,Vincenzo d’Errico and Giuseppe Ricciardi,The new IMGC-02 transportable absolute gravimeter:measurement apparatus and applications in geophysics and volcanology,2008.

〔10〕Ch Rothleitner1,S Svitlov,H M′erim`eche2,H Hu and L J Wang,Development of new free-fall absolute gravimeters,2009.

〔11〕HHu,S Svitlov,C Rothleitner,J Schafer,J Zhang and L J Wang,Improvements of the MPG -2 transportable absolute ballistic gravimeter,2010.

〔12〕Giancarlo D’Agostino,Sergio Desogus,A-lessandro Germak,Claudio Origlia,Danilo Quagliotti,Giovanna Berrino,Gennaro Corrado,Vincenzo d’Errico and Giuseppe Ricciardi,The new IMGC-02 transportable absolutegravimeter:measurementapparatusand applicationsin geophysicsand volcanology,2008.

〔13〕J.E.Faller,Thirty years of progress in absolute gravimetry:a scientific capability implemented bytechnological advances,2002.

TB96

A

1673-260X（2017）09-0036-03

2017-07-02