“实物演示法”在概率论与数理统计教学中的应用

葛梅梅，余晓美

（滁州学院 数学与金融学院，安徽 滁州239000）

“实物演示法”在概率论与数理统计教学中的应用

葛梅梅，余晓美

（滁州学院 数学与金融学院，安徽 滁州239000）

《概率论与数理统计》是一门应用性很强的课程[1]，课程中的基本概念和基本模型比较复杂、抽象，为了让学生更好地理解基本概念和基本模型，采用"实物演示法"进行教学，以典型的教学问题-盒子模型为例，最后将其推广到抽签模型和最大似然估计.

概率论与数理统计；实物演示法；盒子模型

1 引言

《概率论与数理统计》是研究随机现象的统计规律性的一门学科，它在自然科学、社会科学、工程技术、工农业生产等领域中得到了越来越广泛的应用.这门课程的特征具有丰富的背景、巧妙的思维和有趣的结论，学生可以在浓厚的兴趣中学习和掌握《概率论与数理统计》的知识.因此，在我国高等学校的绝大多数专业的教学中，《概率论与数理统计》均列为必修课程或限定选修课程，尤其是应用型本科院校，更加要重视这门课程的教学.

长期的教学实践，我们发现，在这门课程的教学中，存在着几个棘手的问题，首先，目前非数学专业的概率论与数理统计教材中，普遍存在着“理论较多，理解困难”的问题.这些问题导致学生兴趣不足，不能学以致用.其次，《概率论与数理统计》课程通常在大二第一学期开设，课程内容在涉及到二重积分的二维随机变量、期望、方差等部分时，要用到学生在大一时学习的高等数学知识，但此时大部分学生已经遗忘得差不多了，最后，学校有很多文科类，文科生在高中时是没有学过排列组合的知识或对此只是略有了解，但是在讲授排列组合内容（如古典概型、二项分布、全概率公式等）的知识时，需要学生具备基础的排列组合的知识，尤其是文理兼收的班级在讲授这部分知识时教学就显得格外困难.这些问题导致学生学习这门课程时出现畏难情绪，课堂学习的参与度低，这就要求教师探索新的教学方法，力图将知识用最简单直观的方式讲授出来，在这其中，“实物演示法”功不可没，起到了积极的作用.

2 实物演示法及其特点

实物演示法是一种直观形象的教学方法，它的特点是教师通过展示实物、教具和示范性的试验来验证某一事物和现象.演示所使用的工具可分为以下四大类：实物、标本、模型、图片的演示；图表、示意图、地图的演示；实验演示；幻灯片、电影、录像的演示.

在《概率论与数理统计》这门课程的教学过程中，我们借助实物演示引导学生集中注意力，运用多种感官去感知，鼓励学生自己去探索和思考，使得各种概念和定理不再枯燥无味，而是鲜活地呈现在学生眼前.

3 盒子模型的“实物演示法”的教学设计

3.1 提出问题

古典概型中，有一类模型是盒子模型，盒子模型即是涉及将球放入盒子的一类模型.学生对于这类模型的困惑在于，这个模型中既有盒子又有球，学生容易混淆这两个对象，当盒子与球变动时，学生很难找到球放入盒子方法数计算的突破口.所以此时就要求教师必须探索新的教学方法“实物演示法”，将盒子模型的本质用最简单直观的方式讲授出来.下面就来讨论“实物演示法”在盒子模型中的具体应用.

3.1.1 盒子模型问题

有3个球、4个盒子，球与盒子都是可以区分的，每个球都等可能地被放到4个盒子中的每一个，试求：

（1）指定的3个盒子中各有一球的概率；（2）恰有3个盒子各有一球的概率.

3.2 实物演示法的教学设计

课前让学生每人准备4个一次性纸杯（当作盒子），3个小塑料球，接下来就是和同学们一起进行扔球游戏，题目中指出球与盒子都是可以区分的，让学生用黑笔在纸杯上标上序号1、2、3、4，

（1）问中指定的3个盒子，向学生强调盒子是指定的，让学生拿出3个纸杯放在书桌上，三个纸杯就已经确定好了，然后扔球，学生手中3个小塑料球，第一个纸杯有3种放法，第二个纸杯有2种放法，还剩一个小塑料球只能放到最后一个纸杯里（每个小塑料球都等可能地被放到4个盒子中的每一个），故所求概率为

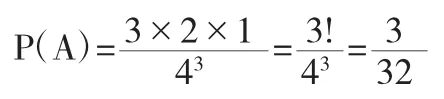
（2）记“恰有3个盒子中各有一球”，与（1）问不同的是纸杯从“指定”变成“恰有”，恰有3个纸杯，纸杯没有选出来，首先要从4个纸杯任选3个纸杯准备放球，共有C43种取法，选完纸杯之后，然后同学们又开始扔球游戏，学生手中有3个小塑料球，第一个纸杯有3种放法，第二个纸杯有2种放法，还剩一个小塑料球只能放到最后一个纸杯里（每个小塑料球都等可能地被放到4个纸杯中的每一个），故所求概率为

立即可以得到一般情况，如下

设有n个球，N个盒子，球与盒子都是可以区分的，每个球都等可能地被放到N个盒子中的每一个，试求：

（1）指定的n个盒子中各有一球的概率；

（2）恰有n个盒子各有一球的概率.

分析：由盒子模型问题一同理推得

（1）记p1=“指定的n个盒子中各有一球”，则有

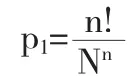
（2）记p2=“恰有n个盒子各有一球”，则有

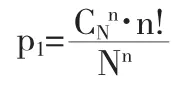
3.3 推广及引申

“实物演示法”也可推广到抽签模型和最大似然估计，利用实物演示向学生讲解知识.

3.3.1 抽签模型

上课前准备10根签，其中有7根白签、3根红签，现在请十名学生随机地一根一根抽签，抽后不放回，谁抽得红签奖励一个小礼物，同学们在底下嘀咕着是不是先抽抽得的红签概率大呢，接下来讨论的问题是让谁先抽才公平呢？

分析：问题转化为第k（k=1,2,3…10）次抽得红签的概率是否相等.把签标上编号，按抽签次序把签排成一排，直到10根签都抽完，将每一个排列作为一个样本点，总数为10根签的全排列数10！，事件Ak=10“第k次抽得红签”相当于在第k位放红签，共有3种放法，每种放法又对应其余9根签的9！种放法，故Ak包含的样本点数为3×9!，因此所求概率为

本题的结果与k（k=1,2,3…10）无关，即不论是第几次，抽得红签的概率都一样，均为红签所占的比例数.可见，抽签不论先后，中签的机会都一样！学生得知这个结论，不再争先恐后地去抽签，而是不慌不忙地去抽签.

3.3.2 最大似然估计

在讲授在参数的点估计中的最大似然估计一节时，学生往往学完之后，只会机械地按步骤求解，对于什么含义，大部分学生是模糊不清的.使用实物就可以帮助学生理解什么是最大似然，上课之前给学生每人发一个刮刮卡，学生刮开之前，问学生刮开之后是什么，学生会回答几乎全是谢谢惠顾，这时候及时问学生为什么你们第一反应是谢谢惠顾而不是中奖呢，因为平时最可能刮到的就是谢谢惠顾，我们就认为谢谢惠顾出现的概率就是最大的，这就是最大似然估计在生活中最简单的体现，同学们在不知不觉中就用到了.这也让学生对最大似然估计原理有直观的印象，即是设一个随机现象有几种可能结果：A,B,C,…,若在一次试验中结果A出现，则一般认为A出现的概率最大.简言之，“在一次试验中发生了的事件概率最大”，下面再来看一个具体的例子.

一袋中装有黑球和白球，其数目之比为1:9，但不知道是黑球多还是白球多.若以p表示从袋中任取一球为黑球的概率，则p可能是0.1，也可能是0.9.现从袋中有放回地取2只球，结果全是黑球，问p的估计值应取0.1还是0.9？

分析：以X表示从袋中任取一球为黑球的只数，即

则XB（1，p），即

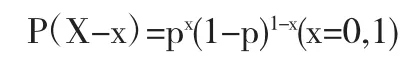
由题设知，在对总体X进行的一次抽样中，取到了样本值(x1,x2)=(1,1),故该样本值出现的概率为

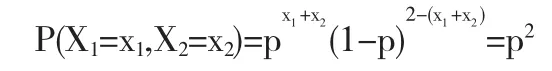
记为L(p)，其中p是未知参数，即

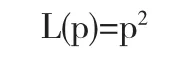
由此一来，学生一下子就会觉得最大似然估计不是那么高深的概念了.

4 “实物演示法”的教学效果

这种让学生亲自体验的实物演示教学方法，既可以激发学生学习的兴趣，又可以让学生更容易接受教学内容.学以致用是教学的最高境界，学生从实物演示中亲自获得的知识，更容易在头脑中留下印象，也更容易学以致用.此在教学过程中要从学生的实际情况出发，通过实物演示教学有效地和学生互动、活跃课堂气氛，消除学生学习这门课的畏难情绪，提高学习的积极性与参与度．其次，合适的实物演示法可提高学生对概念的快速理解与应用.同时该课程本身的特点也是贴近实际应用，这样一来，实物演示法更能发挥它的优越性，通过实物让学生感知知识，有效地降低了其枯燥性、抽象度.

总而言之，课堂教学不是要抽象化、数学化，而是要实物化、具体化.实物演示法就是运用多种感官去感知，鼓励学生自己去探索和思考，使得各种概念和定理不再枯燥无味，极大提高了学生的学习兴趣.

〔1〕马阳明,朱方霞,陈佩树.应用概率与数理统计[M].合肥：中国科学技术大学出版社，2013.

〔2〕王利超,吕丹,刘婷.“案例教学法”在概率论与数理统计教学中的应用[J].统计教研，2009（1）:42-43.

〔3〕茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社，2004.

〔4〕秦玉芳,丁艳凤,郑晓琪.浅谈情景教学法在概率论与数理统计中的应用[J].高教学刊，2016(15)：113-114.

〔5〕李晓彬.案例教学在《概率论与数理统计》中的应用及思考[J].兰州文理学院学报（自然科学版），2014,28(5).

O211.1

A

1673-260X（2017）09-0005-02

2017-06-17

滁州学院多元统计分析课程综合改革项目（2016kcgg008）;滁州学院统计学课程综合改革项目（2016kcgg007）;滁州学院科学研究项目-混合序列的强收敛性及在半参数回归模型中的相合估计（2015GH35）;滁州学院科学研究项目:时间序列长记忆性和波动聚集性研究——基于ARFIMA-GARCH模型研究（2014GH34）