树上限制性k-node multicut问题的近似算法

杨惠娟，董延寿，林仕勋

（昭通学院 数学与统计学院，云南 昭通657000）

树上限制性k-node multicut问题的近似算法

杨惠娟，董延寿，林仕勋

（昭通学院 数学与统计学院，云南 昭通657000）

树上的限制性k-node multicut问题(k-CMC(T))是NP难的,针对k-CMC(T)问题本文首先将问题分解成若干个最大流问题设计了近似值为k的算法其中k是参数.其次利用树的性质改进算法降低了算法的时间复杂度得到一个时间度为O(|V|3log2|V|)且近似值不变的算法.算法简单、易懂.

限制性k-node multicut；近似算法；树；最大流

1 引言

原始的multicut问题（MC)是图论与组合优化中比较活跃和经典的一类问题,原始的multicut问题分为edge multicut问题(EMC)和node multicut问题(NMC).它们在现实中的应用广泛，特别是在城市建设,道路规划,通讯等方面.近几十年来一直受到广泛关注,但是随着对问题的不断深入，许多研究者对原始的multicut问题（MC)的提法或目标进行改动，这就产生了一些比较复杂的推广问题如k-edge multicut问题(k-EMC)问题和k-node multicut问题(k-NMC)问题等这些推广问题都是NP难,因此与其花大量的时间去找一个最优解,倒不如在多项式时间内去找一个近似度较好的可行解.

一般图上multicut问题及它的推广问题的求解是非常难的,因此很多研究者将它限制在特殊图上进行研究.Guo和Huffner等在文献[1]中证明了区间图上的无限制性node multicut是NP难的,限制性的node multicut是多项式可解的.Papadopulos[2]研究了置换图上的限制性node multicut问题并且给出了一个多项式时间算法去求得最优解.对于树上的edge multicut问题(EMC(T))问题,Garg,Vazirani和Yannakakis在文献[3]中利用线性规划的原始-对偶理论设计了近似值为2的算法,这是EMC(T)问题目前最好的算法且同时证明了即使在高度为1且不赋权（图中每一条边的权重都是1）的树上EMC问题都是NP难和MAX SNP难的.对于树上限制性node multicut问题(NMC(T))问题文献[4]中设计了一个近似比为2的算法.Levin和Segev在文献[5]中考虑了Prize-Collecting版本的树上的edge multicut问题(pc-EMCP(T)),他们将pc-EMCP(T)问题归约到EMCP(T)并证明了文献[1]中设计的算法对pc-EMCP(T)具有拉格朗日乘数保持性质.树上的k-edge multicut问题Mestre[6]设计了一个近似值为2+ε的近似算法，树上推广的k-edgemulticut问题文献[7]中设计了一个近似值为的近似算法.

2 树上限制性k-node multicut问题的描述及近似算法

任给无向树T=(V,E)以及正整数k和T的q个顶点对构成的集合S={(s1,t1),(s2,t2),…,(sq,tq)},∀i∈{1,2,3,…,q}，si,ti称为终端点,对树T的除终端点外所有的顶点赋一个非负实数w(v),树上限制性k-node multicut问题是求G的一个顶点子集D,并且D满足如下条件:

（1）D不含任何终端点;

（2）S中至少有k个顶点对在G-D中不连通;

我们可将此问题分解成树上的q个最大流问题,则得到一个近似值为k的算法.

算法1:

输入:T=(V,E;w)以及正整数k和q个顶点对构成的集合S={(s1,t1),(s2,t2),…,(sq,tq)}，其中w:V-S→R+

输出:该问题无解或可行解D.

Begin

第1步:∀i∈{1,2,3,…,q}检查Pi上的点是否全是S中的点，如果全是S中的点则令i∈Q若|Q|≥q-k则输出：此问题无解否则令S'=S-{(si,ti)|i∈Q}转到第2步.

第2步:把此问题分解成求|S'|个树T的node multicut问题,然后对S'中的每一个顶点对(si,ti)调用一次求解最大流的Dinic算法[8]求得最小si-ti点割集Di.

第3步:∀(si,ti)∈S'计算按w(Di)从小到大排序,不妨设排序为w(D1)≤w(D2)≤…≤w(D|S'|),令D=D1∪D2∪…∪Dk,输出D.

End

定理3.1算法1得到问题的可行解,并且近似值为k.且时间复杂度为O(|V|4|E|.

证明任给树上限制性k-node multicut问题的一个实例I,设I的最优解为D',即S'中至少有k个顶点对在G-D'中不连通并且达到最小,不妨设(s'1,t'1),(s'2,t'2),…,(s'k,t'k)在G-D'中不连通.因为算法1的第2步调用最大流算法求得的Di是最小si-ti点割集即顶点对(si,ti)在G-Di中不连通,因此在G中去掉D至少使得(s1,t1),(s2,t2),…,(sk,tk)在G-D中不连通,于是D是k-node multicut问题的可行解.假设用最大流算法解得的最小s'i-t'i割集,i=1,2,3…,k最优解为D*i,而D'为可行解所以有w(D*i)≤w(D'),根据算法1第3步有则w(D')≤kw(D'),因此算法1得到的解近似值为k.算法中第1步要考虑所有的路Pi最多有q条路,而每一条路所有的点都要进行检验每一个点检验一次最多有|V|个点,故第1步总的计算量为O(q|V|).第2步对s'中的每一个顶点对调用一次Dinic算法,Dinic算法的时间复杂度为O(|V|2|E|)最多调用q次,因此第2步总的计算量为O(q|V|2|E|).第3步主要在于对w(Di)进行排序,时间复杂度为O(qlog2q).S中的顶点对至多为因此算法总的时间复杂度为

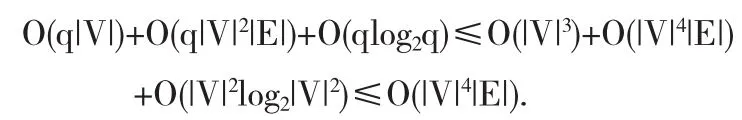
因为我们考虑的图比较特殊是树而树上任意两点之间只有唯一的一条路要想顶点对(si,ti)不连通只要在Pi上去掉一个点即可,不需要花费大量时间去调用最大流算法.因此改进算法如下：

算法2:

输入:T=(V,E;w)以及正整数k和q个顶点对构成的集合S={(s1,t1),(s2,t2),…,(sq,tq)}，其中w:V-S→R+

输出:该问题无解或可行解D.

Begin

第1步:令T1=T[M]即T1是T的由顶点集M导出的子图,检查T中Pi上的点是否全是T1中的点,如果全是T1中的点则令i∈Q若|Q|≥q-k则输出：此问题无解否则令S'=S-{(si-ti)|i∈Q}转到第2步.

第2步:对S'中的每一个顶点对(si,ti)所对应的路Pi上的非终端点按权重进行升序排序.将权重最小的点放入D',若某一条Pi上有多个点权重同时小的点只需放入一个点即可.每一条路上放入D'中一个点.

第3步:对D'中的点按权重进行升序排序,不妨设排序为w(v1)≤w(v2)≤…≤w(v|S'|),令D={v1,v2,…,vk},输出D.

End

定理3.2算法2得到问题的可行解,并且近似值为k.且时间复杂度为O(|V|3log2|V|).

证明根据算法1的证明方法可证得算法2得到的解是可行解并且近似值为k.算法第1步首先构造由顶点集M导出的子图T1,方法可以删掉所有非终端点及所有与非终端点相关联的边,而树T中边的数目|E|=|V|-1,因此这一步的计算量O(|V|2),其次考虑所有的路Pi最多有q条路,而每一条路所有的点都要进行检验每一个点检验一次最多有|V|个点,故第1步总的计算量为O(q|V|).第2步的主要计算量在于对S'中的每一个顶点对(si,ti)所对应的路Pi上的非终端点按权重进行排序,排序一次的时间复杂度为O(|V|log2|V|),总共需要迭代q次,总得计算量为O(q|V|log2|V|).第3步主要在于对D'中的点进行排序时间复杂度为O(qlog2q).S中的顶点对至多为.因此算法总的时间复杂度为:

5 结论

本文主要提出并研究了树上限制性k-node multicut问题.首先将问题分解成若干个最大流问题设计了近似值为的算法.算法时间复杂度虽然是实例规模的多项式,但是随着图的规模的增大运行算法时依然浪费了大量时间.其次结合了树的性质改进算法降低了算法的时间复杂度得到一个时间度为O(|V|3log2|V|)且近似值不变的算法.本文所设计的两个算法虽然近似值都是k,它是一个参数与输入的实例规模有关,因此实例不一样近似值也就不一样.如何进一步改进算法使算法的近似值是一个固定常数与实例的规模无关是我们今后将要努力的方向.

〔1〕J.Guo ,F.Huffner ,E.Kenar,R.Niedermeier,J.Uhlmann.Complexity and exact algorithms for vertex multicut in interval and bounded treewidth graphs[J].European Journal of Operational Research 186 2008,542-553.

〔2〕Charis Papadopoulos.Restricted vertex multicut on permutation graphs [J].Discrete Applied Mathematics 1602012, 1791-1797.

〔3〕N. Garg, V. Vazirani and M. Yannakakis. Primal-dual approximation algorithms for integral flow and multicut in trees[J].Algorithmica 1997, 18, 3-20.

〔4〕杨惠娟.树上的限制性node multicut问题[J].大理学院学报（自然科学版），2014（12）.

〔5〕Levin A,Segev D.Partial multicuts in trees [C]//Proe of the 3rd workshop on Approximation and online Algorithms(WAOA).Berlin:Springes 2005:320-333.

〔6〕Julian Mestre,Lagrangian relaxation and partial cover(extended abstract)[J].Theoretical Aspects of Computer Science,STACC 2008 ,25:539-550.

〔7〕Peng Zhang ,Daming Zhu ,Junfeng Luan.An approximation algorithm for the Generalized k-Multicut problem[J].Discrete Applied Mathematics 2012 ,160 :1240-1247.

〔8〕高随祥.图论与网络流理论[M].北京:高等教育出版社,2009.308.

O157.5

A

1673-260X（2017）09-0007-02

2017-06-08

云南省教育厅科学研究基金项目（2016ZDX152)；昭通学院一般项目（2016xj31）