基于余枝搜索的最小独立闭合环自动搜索算法

谢海燕，王 超

(上海岩土工程勘察设计研究院有限公司,上海 200438)

基于余枝搜索的最小独立闭合环自动搜索算法

谢海燕，王 超

(上海岩土工程勘察设计研究院有限公司,上海 200438)

在控制测量、水准测量数据处理中，为实现快速有效的进行最小独立闭合环的自动搜索，基于生成树和余树，利用数组的存储结构，由余枝两端向外搜索，遇同名点后获得闭合环，再通过闭合环的独立性判断，实现最小独立闭合环的快速有效搜索.进而利用该程序对2011年上海市闸北区水利普查项目中的部分水准测量结果进行进行验证，证明所搜索的闭合环在常规网型中可以有效的做到最小和独立.

最小独立闭合环；生成树；自动搜索；算法

在测量的数据处理中，为保证平差结果的正确性，防止观测值可能含有粗差及系统误差影响平差结果，无论是导线网、水准网，还是GPS控制网，都需要对控制网中的各种多边形进行闭合差检核，以探测、剔除粗差，并评定观测值的质量[1].最小独立闭合环的确定是这一工作得以展开的首要工作，通常通过手工方法虽然也能完成闭合环的确定，但对于较为复杂的网型而言，这种方法容易出错，且不易做到最小性与独立性，而且数据处理时其效率较为低下，不能满足高质、高效的要求.因此，在进行最小独立闭合环搜索时，利用计算机实现最小独立闭合环的自动生成在数据处理中具有重要意义.

利用计算机进行最小独立闭合环的搜索时一般有以下几种方法：李光炎等[2]阐释了基于邻接矩阵变换的闭合环搜索算法；白征东[3]给出了基于深度优先的闭合环搜索算法；吕光楣[4]将网型信息简化为拓扑图，利用图论的相关算法知识进行搜索；姚连璧[5]利用网型信息构建一生成树，同时得到余枝信息，然后以余枝为基础搜索最小独立闭合环；赵一晗等[6]确定了基于邻接矩阵的搜索算法.这些方法虽然都实现了最小独立闭合环的自动搜索，但其各具优缺点.基于邻接矩阵的搜索算法虽然简单，但其时间复杂性与空间复杂性高，导致其计算时间长、效率较低；基于深度优先算法，在采用邻接表后，虽节省时间和空间，但在判断两端点是否直连时，不太方便；对于利用图论的相关算法进行搜索，编程复杂，不易实现；基于生成树和余树搜索算法虽然理论简单，但该搜索算法还可以进一步优化.

本文是基于生成树和余树搜索算法，利用二维数组存储结构，将原先由余枝一端先搜索闭合环，再判断选择的基本思路，改为由余枝两端同时搜索对方端点，遇同名点即得最小闭合环，最后再通过独立性判断，实现最小独立闭合环的自动搜索.本方法避免了原算法中将其它边数较大的闭合环先搜索出来再排除的冗余计算，从而在一定程度上减少了计算量，在闭合环独立性分析中，给出了几类较常见的独立性问题，并给出了相应的解决方法，最终实现最小独立闭合环的自动搜索.

1 生成树和余枝搜索算法原理

1.1 最优树的建立算法

面对一个网型，可以建立很多种树.为了有利于闭合环的搜索，所建立的树应使得构成基本环路的支路数目尽可能地少，并称这样的树为最优树.其具体建立步骤为[7]：

(1)计算网中各个节点(指网中所有点)的度，并找出度最大的结点，度最大的结点不止一个时，此时可任意选取一个，假设该点为V.

(2)以网中度最大的接点为起点，即先访问度最大的结点，再访问该点的邻节点V1，V2，…，且记录相应的邻接边.

(3)分别从V1，V2，…出发，访问它们未被访问过的邻接点，记录相应的邻接边.

(4)若此时尚有未被访问过的接点，则继续访问下一级邻接点，直到所有的结点都被访问过为止.

以上算法搜索出的树枝的集合即为所建立的最优树，同时，网中未被访问过的边组成的集合即为余枝.基于余枝搜算法正是在所建立的最优树枝和余枝的基础上进行的.利用已经建立的最优树的余枝进行搜索，一方面，可以利用余枝的独立性来达到所搜索闭合环的独立性；另一方面，可以利用余枝数目同最小独立闭合环的数目相同来达到搜索的全面性.基于本余枝搜索的算法，在此处进行调整，得到适合数组存储结构的新算法.

1.2 最小独立闭合环

最小独立闭合环的选取必须满足以下3个条件：

(1)所有闭合环应该是相互独立(线性无关)的，任何一个闭合环都不能由其它闭合环线性合成；

(2)闭合环中包含的边数最少，这样可以提高探测粗差的能力；

(3)对于边数相同的闭合环，应取长度最短的环.

上述方法是姚连璧等[8]给出的一种典型的独立闭合环的搜索算法，本文算法在此算法的基础上进行了改进优化.

1.3 多边形独立闭合环数

皱进贵等[9]给出了最小独立闭合环数确定的方法.对于一个有n个测站点，其中有任意一个点的高程为已知，m条观测边的高程控制网，其必要的观测个数为n-1，实际观测个数为m，故其自由度(条件方程个数)为m-(n-1)，即m-n+1个.在图网G=(n,m)中，由图论知识可知，非生成树边的个数必为m-n+1个，因此所有最小独立闭合环的个数为m-n+1.

2 基于余枝搜索的闭合环搜索算法

2.1 算法原理

传统的余枝搜索算法在进行独立闭合环的搜索时，虽然其能够实现闭合环的搜索，但该方法将包括余枝的所有闭合环都搜索出来，然后选择合适的环.而在实际生产应用中，并不需要包含余枝的所有闭合环，一般只需要边数最小的独立环.为此，本文设计从余枝的两边同时向外搜索，遇到同名点则停止，如此既避免了对其它无用环的搜索，同时减小了程序的运算量，再则所得闭合环可以保证边数最小.以下算法根据图1中的水准网给出了相应的算法步骤.

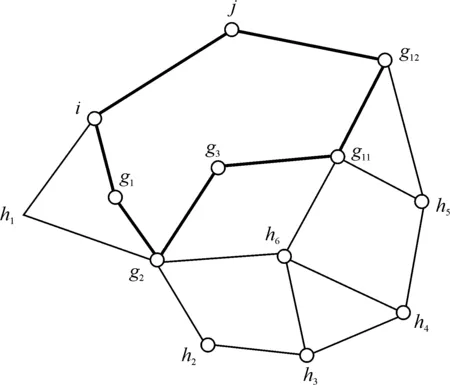
图1 水准网例图

(1)建立最优树并将树枝信息存于数组B中，同时得到余枝，余枝信息存于数组A中.

(2)以余枝(i，j)的两端点为搜索起点，以i为起点搜索其邻节点g1、h1、j…，剔除节点j，搜索信息存放于数组C中；以j为起点搜索其邻节点h1、g12、i…，剔除节点i，信息存放于数组D中.在存储搜索信息的数组中，第一列存放余枝的起点，后续的每一列均为前一列的邻节点，每一列代表一种可能路径.设置整数n，表示第n次遇到同名点时停止搜索(一般为1，特殊情况n加1).

(3)比较新搜索出的相邻节点间有无同名点，若有n减1.若n=0时，停止搜索，n>0则转下一步.

(4)以C的最后一列节点分别为起点，搜索其邻节点，并存于C的下一列中，以C的当前最后一列和D的倒数第二列和倒数第一列比较，遇同名点n减1，同时判断是否停止；若没有同名点则以D的最后列分为起点，搜索其邻节点，并存于D的下一列中，以D的当前最后一列和C的倒数第二非零列和倒数第一非零列比较，若遇同名点n减1，并判断是否停止.

(5)重复第四步直到搜索到符合要求的闭合环，将C、D数组中对应有同名点的相应行摘录出，即可组成该余枝下边数最少的闭合环，将余枝和其对应环存入数组E中.

(6)对于E中一条余枝对应一个环的，优先选择存入最小独立环数组F中，在存储时要判断和F中已有环之间的独立性；若某条余枝对应多条闭合环的，逐个将各环和F中的入选环比较，若其和某一环是同一环的则删除.若比较结束后该余枝对应的闭合环还不唯一，则计算各环距离，取距离最短的存入F中.

(7)若经过第(6)步的比较，某一余枝对应环全部被删除时，n加1，对于该余枝需要再次搜索，重复上述步骤直到得到合格的闭合环.

本算法的对应流程图(见图2).

2.2 独立性判断

基于上述算法，虽然对于一条余枝可以搜索出一条闭合环，但在独立性方面还无法保证.包含余枝的闭合环之间不一定是独立环，因为在某些情况下，包含本条余枝的情况下可能还包含有其它的余枝，同时这两条余枝所搜索出的闭合环有可能是同一条闭合环.

根据图3所示，黑色实线为树枝，虚线为余枝.图3中，余枝(8,9)和余枝(9,10)在搜索时所得到的闭合环为8-10-9-8和9-8-10-9，虽然都包含各自的余枝，但它们实质为同一环，这对于本文所要求的独立性还不满足,这是此类方法所遇到的第一类独立性问题.为此，在以余枝进行搜索时，每搜索出新的闭合环，将其与已经搜索出的闭合环中边数相同的环比较，当包含相同节点名的应当剔除，如此可消除上述提出的第一类独立性问题.

图2 最小独立闭合环自动搜索算法图

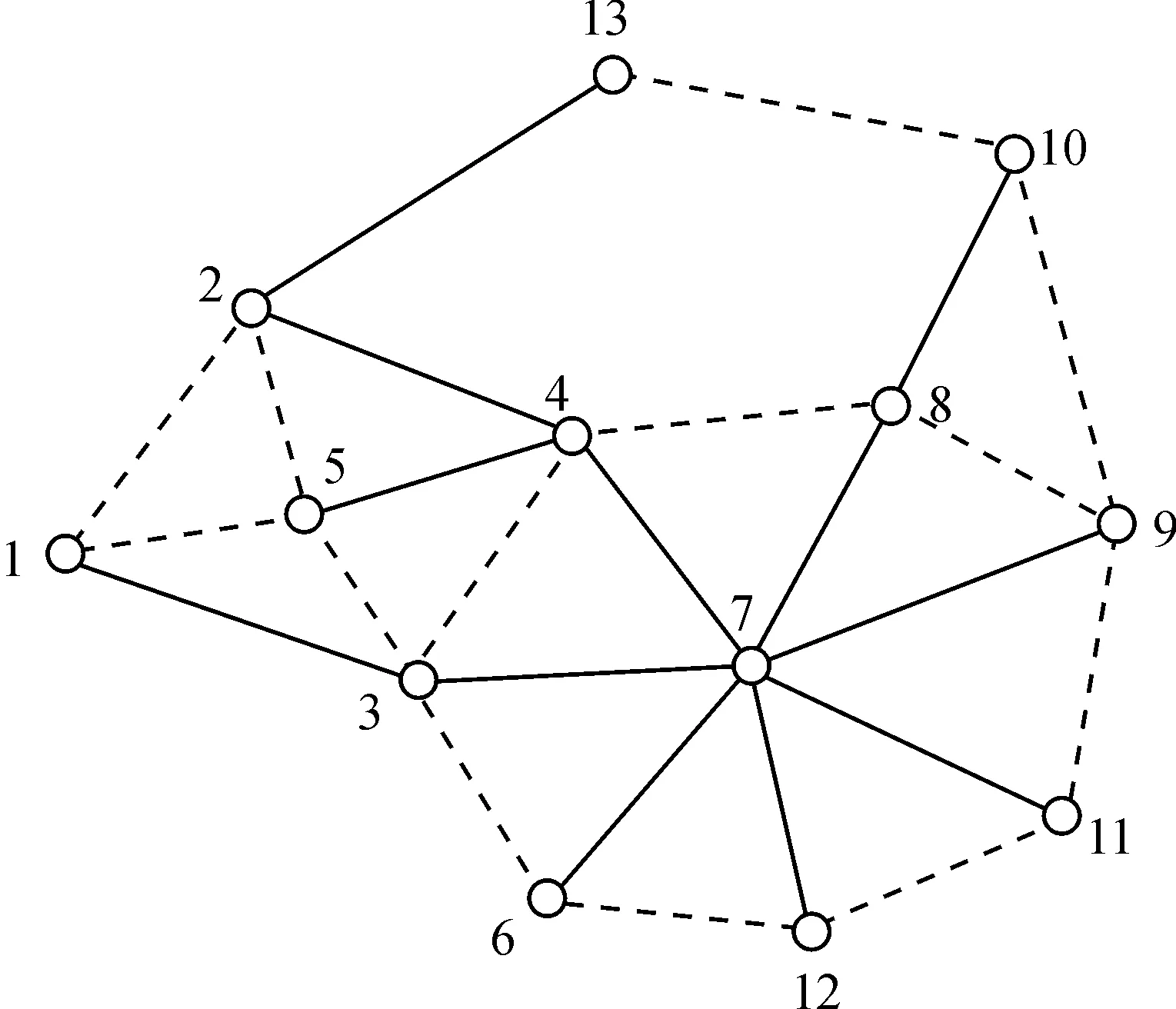
图3 图1最优树

第二类独立性问题是上述算法第(7)步所谓的特殊情况.对于这种情况，可将这种余枝单独重新搜索，逐渐增加它同名点相遇的次数(n++)，以此扩大环的边数，得到其它的独立环，以实现每条余枝都能搜索到一条闭合环.

在进行独立性判断时，主要是判断当前的环和已经判断筛选过的环之间是否独立.对于某些特殊的余枝，它们需要通过增大相遇点的次数来得到闭合环.为避免所得到的环由其它独立环线性组合的情况，也可以由该余枝通过树枝去搜索，在第一次遇到同名点时获取闭合环，而且可以肯定该环和其它环一定是独立的.这种办法虽然能保证独立性，但所得到的闭合环不一定是最小的.

对于上述方法，由于是从余枝两端向外搜索，遇到同名点则停止，个别特殊的余枝需要增加所遇到同名点的次数经搜索后停止，因此所搜索的闭合环边数满足最小.在独立性方面，由于每个环包含一条不为其它环所具有的余枝，因此满足独立性的要求.

3 算 例

根据上述算法，编制了最小独立闭合环的自动搜索程序.下面利用该程序针对2011年海市闸北区水利普查项目中的部分水准测量结果进行水准环自动搜索，实测水准网图(见图4).搜索结果为：

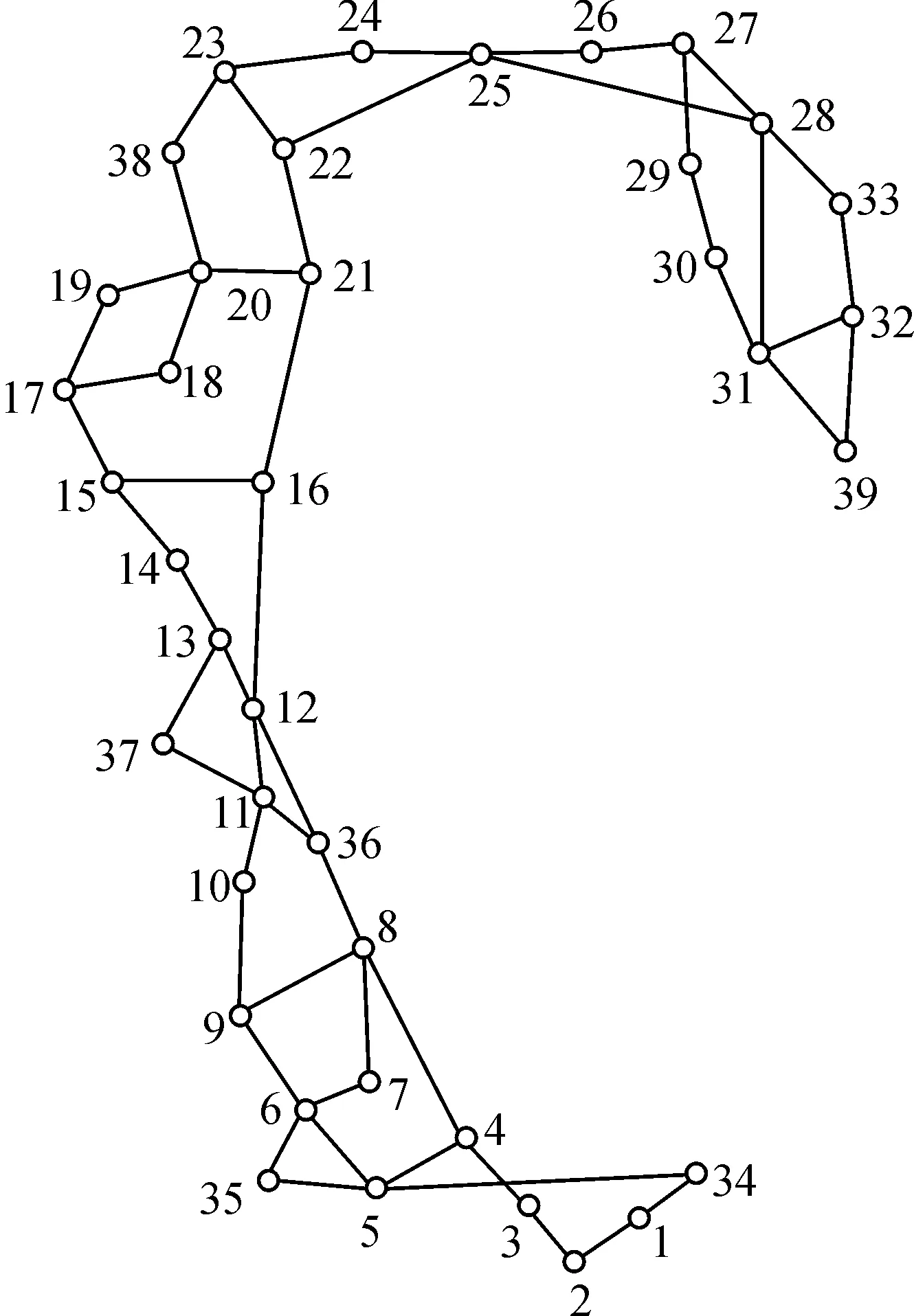
图4 实测水准网图

经核查，该方法所搜索出的闭合环均满足边数最小，闭合环数目亦符合理论要求，且各环之间互相独立.

4 结 论

本文根据测量控制网的特点，以数组的存储结构，给出了一种新的余枝搜索算法.为避免原先算法计算量大、效率低下的缺点，同时考虑到所需闭合环最小的特点，采用由余枝两端双向搜索、寻求同点的思路设计算法，最终实现最小闭合环的搜索.本文针对本算法的独立性展开进一步的分析，列举了2种比较特殊的情况，并给出了较为有效的解决方法.本算法避开了深奥的理论知识，以直观、易于理解的逻辑判断进行搜索，对于所搜索的闭合环在常规网型中可以有效地做到最小和独立，算例部分也正验证了这一点.

[1] 叶宝义,陈 义.基于边集数组的最小独立闭合环搜索算法实现[J].测绘通报，2010(12):37-39.

[2] 李光炎,王解先.闭合环搜索方法的探讨[J].工程勘察,2004(6)：52-53.

[3] 白征东.GPS网中最小独立闭合环的自动搜索[J].测绘科技动态，1994(2)：18-21.

[4] 吕光楣.单源点最短路径的一种新算法[J].微机算机应用，1990(2):51-54.

[5] 姚连璧.平面控制网闭合环的自动寻找[J].铁道勘察，2006(12)：55-58.

[6] 赵一晗,伍吉仓.控制网闭合环搜索算法的探讨[J].铁道勘察，2006,32(3)：12-14.

[7] 欧 龙.一种新的闭合环自动搜索算法[J].柳州师专学报,2014,29(1):117-120.

[8] 姚连璧,周小平.基于MATLAB的控制网平差程序设计[M].上海：同济大学出版社，2006.

[9] 皱进贵,冯 晨.控制网最小独立闭合环搜索算法研究[J].地理空间信息，2008,6(6)：97-99.

A Method of Auto-searching Least Closed Loops Based on Spare Branch

XIE Hai-yan, WANG Chao

(Shanghai Investigation and Design Institute Co., Ltd. of Geotechnical Engineering, Shanghai 200438, China)

In the data processing of control surveying and leveling, in order to quickly and effectively carry out auto-search least closed loop, based on spanning tree and spare branch, a 2-D array storage structure is used to search at both ends of spare branch and to get closed loop when meeting the same point. The independent judge of the new closed loop realizes fast and effective auto-searching least closed loops, which is proved to be effective by some leveling results of water census in Zhabei district of Shanghai city.

the least closed loop; the spanning tree; automatic searching; algorithm

P211

A

1008-536X(2017)03-0068-04

2017-02-13

谢海燕(1983-)，男，江西吉安人，工程师，研究方向为工程测量、变形测量.