基于地理加权回归模型的省级TRMM降水数据降尺度研究

金辉明，徐 鹏，何 康，许金涛，马自强

(1.浙江省水文局 浙江 杭州 310009;2.浙江耘图信息科技有限公司,浙江 杭州 310053；3.浙江大学 环境与资源学院，浙江 杭州 310058)

基于地理加权回归模型的省级TRMM降水数据降尺度研究

金辉明1，徐 鹏2，何 康3，许金涛3，马自强3

(1.浙江省水文局 浙江 杭州 310009;2.浙江耘图信息科技有限公司,浙江 杭州 310053；3.浙江大学 环境与资源学院，浙江 杭州 310058)

以2011—2013年浙江省地面监测站点降水数据为因变量，TRMM降水数据为自变量进行TRMM数据精度验证，结果表明两者存在比较明显的线性相关性.使用NDVI数据为空间因素，基于GWR模型进行TRMM数据的降尺度操作，三个典型年的降尺度结果与地面数据间的相关系数稳定在0.8左右，呈现良好的线性相关性，且降尺度后相关系数R提升，相对误差BIAS、均方根误差RMSE都有所降低.基于GWR模型的降尺度牺牲一部分数据精度为代价，可以提高TRMM数据的空间分辨率，同时使其能更好地表现变量的空间非平稳性.

GWR；TRMM；NDVI；降尺度；浙江省

降水是地球水循环过程中的重要一环，在水文学、气象学、农业科学等研究领域具有重要意义.通过传统的基于地面气象监测站点的方式获取的降水数据，能够较精确地表征某一点位的降水情况，并可以使用空间插值的方法进一步表现研究区域的降水信息[1].但是地面站点通常在站点数量、地理位置分布、观测数据完整性与连续性等方面存在难以规避的不足，不能很好地反映降水的空间变异性，且由空间插值得到的降水信息可能与实际情况存在较大的误差.与之相比，覆盖面积广、观测数据完整连续的卫星遥感降水数据，在研究大区域降水方面无疑具有更大的优势[2].

1 国内外研究趋势

随着卫星遥感技术的快速发展，利用遥感数据产品对降水信息进行监测和反演，逐渐成为国内外研究、应用的热点方向.某些搭载于特定卫星上的传感器，已是提供空间化降水数据的重要来源[3].这些降水遥感数据产品包括全球降水气候计划(global precipitation climatology project,GPCP)、全球卫星降水制图计划(global satellite mapping of precipitation,GSMaP)、热带降雨计划(tropical rainfall measuring mission,TRMM)等等.国内外的科研人员通过使用这些数据，开展了一系列诸如精度校验、模型构建等研究[4-10].本文的降水数据来自热带降雨计划卫星，该气象卫星由美国国家航空航天局(national aeronautics and space administration,NASA)和日本宇宙航空研究开发机构(Japan aerospace exploration agency,JAXA)联合研制，于1997年11月成功发射.良好的工作状态使得TRMM卫星的使用寿命远超其3年的设计寿命，提供了长达17年的降水数据，为全球与降水相关的科学研究提供了数据保障[11].TRMM降水数据与其他遥感降水产品相比，具有较高的空间分辨率(0.25°×0.25°)，即每一栅格代表实地范围为27.5 km×27.5 km，但是在用于区域尺度的降水空间变异性以及空间分布的研究时，该空间分辨率就稍显粗糙，因此有必要对TRMM降水数据进行降尺度处理，以提高其空间分辨率[12].

利用降尺度技术提高气温、降水等中低空间分辨率的遥感数据，是根据高空间分辨率的环境变量，例如归一化植被指数(normalized difference vegetation index,NDVI)、数字高程模型(digital elevation model,DEM)，与中低分辨率遥感数据建立两者之间的经验方程，然后通过该方程反演得到较高分辨率的气温、降水等数据.近年来，针对TRMM数据的降尺度研究颇有成果，研究人员针对不同的环境变量，建立对应的回归方程，通过反演计算得到了较高空间分辨率的降水数据[13-15].

近年的研究中，常用的降尺度模型有2种，即一般线性回归(linear regression，LR)模型和地理加权回归(geographically weighted regression，GWR)模型.一般线性回归模型是空间数据分析中最常用的统计方法之一，具有较为完善的理论体系和统计推断.它通常使用普通最小二乘法(ordinary least squares,OLS)，假定变量内部以及变量之间具有空间同质性，因此模型的回归方程的参数在整个研究区域内就是确定的常数.使用一般线性回归模型进行全局角度的降尺度处理，虽然在操作上简便易行且计算量小，但其忽略了空间数据的空间非平稳性(spatial nonstationarity)，掩盖了变量在局部的特性[16].地理加权回归模型是一般线性回归模型的延伸，它将空间结构嵌入线性回归模型中，使得空间因素作为回归方程的参数，强调了变量的局部特性，增强了回归结果的可信度[17].

本文以浙江省为研究区域，基于GWR模型和NDVI植被指数数据，对TRMM数据进行降尺度处理，以得到空间分辨率较高、局部特征明显的降水数据，用于研究浙江地区降水的空间分布和空间异质性.

2 研究区概况与数据源介绍

2.1 研究区概况

浙江省位于东经118°01′～123°08′，北纬27°01′～31°10′，地处我国东部沿海、欧亚大陆与西北太平洋的过渡地带.浙江地形复杂，气候局地性特征很明显，全年冬夏较长、春秋短促，属于典型的亚热带季风气候区[18].浙江省温和湿润，年平均温度在16～19 ℃，自南向北递减，年等温线走向大致与纬度线平行；年平均相对湿度较高，在75%以上，年降水日数在140～180 d，多年平均降水量在1 100～2 200 mm之间，不过全省降水地区分布不均，时空变化较大，7、8月份常出现伏旱，9、10月份又出现秋旱，锋面气旋和台风在浙江省活动频繁[19-20].由于独特的地理位置和气候条件，浙江历来是各类气象灾害频发地区，是我国受台风、暴雨、洪涝、干旱影响最为严重的地区之一.因此，本文对浙江省地区降水进行研究很有必要.

2.2 数据源介绍

本文使用的TRMM数据为TRMM卫星第7版本3级产品(3B43 Version7)的月降水数据，数据来自NASA，空间分辨率为0.25°×0.25°，时间分辨率为1个月，数据覆盖浙江全省，数据年份为2011—2013年.地面站点降水资料来自浙江省水文局，资料包含浙江省150个站点2011—2013年降水数据(见图1).NDVI数据来自terra卫星MODIS传感器的MOD13A3植被指数数据，空间分辨率为1 km，时间分辨率为1个月.DEM数据由NASA提供，空间分辨率为90 m.

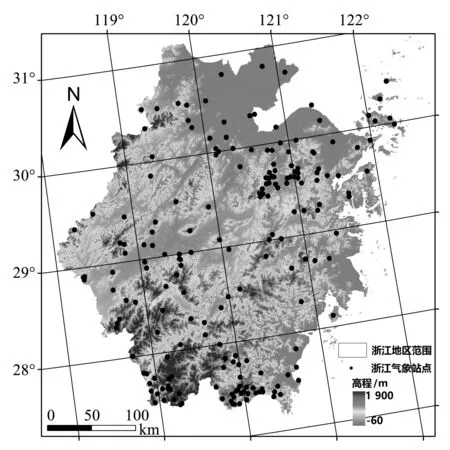
图1 研究区位置与降水监测站点分布

针对下载得到的数据进行波段提取、图层拼接、投影转换、图层裁剪等操作，得到浙江省2011—2013年TRMM月降水数据、NDVI月数据以及DEM数据.将一年中的TRMM月数据算术求和，得到TRMM年降水数据.对一年中的NDVI月数据求算术平均值，得到NDVI年数据.最后，在ArcGIS中，通过DEM数据计算提取坡度和坡向数据.

3 GWR模型的降尺度分析

相关系数R、相对误差BIAS以及均方根误差RMSE是评判回归模型反演结果的常用指标参数.本文使用相关系数R表现地面站点实测降水量与TRMM年降水量数据的线性相关性；使用相对误差BIAS评价实测数据与降尺度后数据的偏离程度；使用均方根误差RMSE反映误差的整体水平.3个指标的计算公式为：

相关系数R=

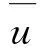
3.1 地理加权回归(GWR)模型

Brunsdon等[17]于1996年提出了地理加权回归(GWR)模型，它通过将空间结构嵌入线性回归模型中，以此来探测空间关系的非平稳性.由于GWR模型不仅在计算上简单易行，回归估计结果有明确的解析表示，而且得到的参数估计还能进行统计检验，因此得到越来越多的研究和应用.GWR模型公式如下.

式中：yi—第i个点的降水量；a0i—第i个点的常数项回归参数；ui,vi—第i个点的空间坐标(如经纬度或大地坐标等)；

aji—第j个空间因素(如NDVI或DEM等)在第i个点的回归参数；

k—空间因素的个数；

xji—第j个空间因素在第i个点处的值；

σ—第i个点的残差值.

本文使用NDVI数据与TRMM降水数据结合，构建GWR模型进行降尺度处理，因此空间因素只有NDVI一种，式(4)可以简化为式(5).

一般线性回归模型的回归系数是不存在空间异质性的，即每一空间坐标点的回归系数保持不变.而在理论上GWR模型不同坐标点的回归系数是不同的，这也是GWR模型优于一般线性回归模型的特点之一.

3.2 降尺度方法

本文通过使用GWR模型，建立起同一典型年的TRMM降水数据与NDVI植被指数数据的函数关系，从而实现降尺度操作.具体操作步骤为：

(1)使用栅格数据重采样技术，将空间分辨率为1 km的NDVI数据转换成分辨率为0.25°的数据.

(2)将尺度一致的TRMM数据与NDVI数据(空间分辨率均为0.25°)作为输入，构建GWR模型.从回归模型中提取每一栅格中心点对应的常数项、NDVI系数项以及残差项.

(3)将提取得到的常数项、NDVI系数项以及残差项这3个矢量数据栅格化，并重采样为分辨率1 km的数据.

(4)根据上述公式(5)，根据每一栅格的NDVI数据计算得到预测降水值，最终得到空间分辨率为1 km的降水数据.

3.3 TRMM数据降尺度的GWR模型分析

3.3.1 典型年TRMM数据精度分析

以2011—2013年浙江省TRMM降水数据为因变量，对应年份全省150个气象监测站点的年降水量数据为自变量，建立一元线性回归方程，验证TRMM数据的精度.由图2可知，2011年TRMM降水数据与地面站点观测数据之间的决定系数R2=0.463 1，一次项系数K=0.829 3；2012年两者的决定系数R2=0.455 5，一次项系数K=0.816 7；2013年两者的决定系数R2=0.343 3，一次项系数K=0.572 4.根据以上3年的数据，TRMM降水数据与观测数据之间存在不低的线性相关性.2011年与2012年的相关程度持平，且略高于2013年.3年的拟合结果都显示TRMM降水数据较实测数据偏大.

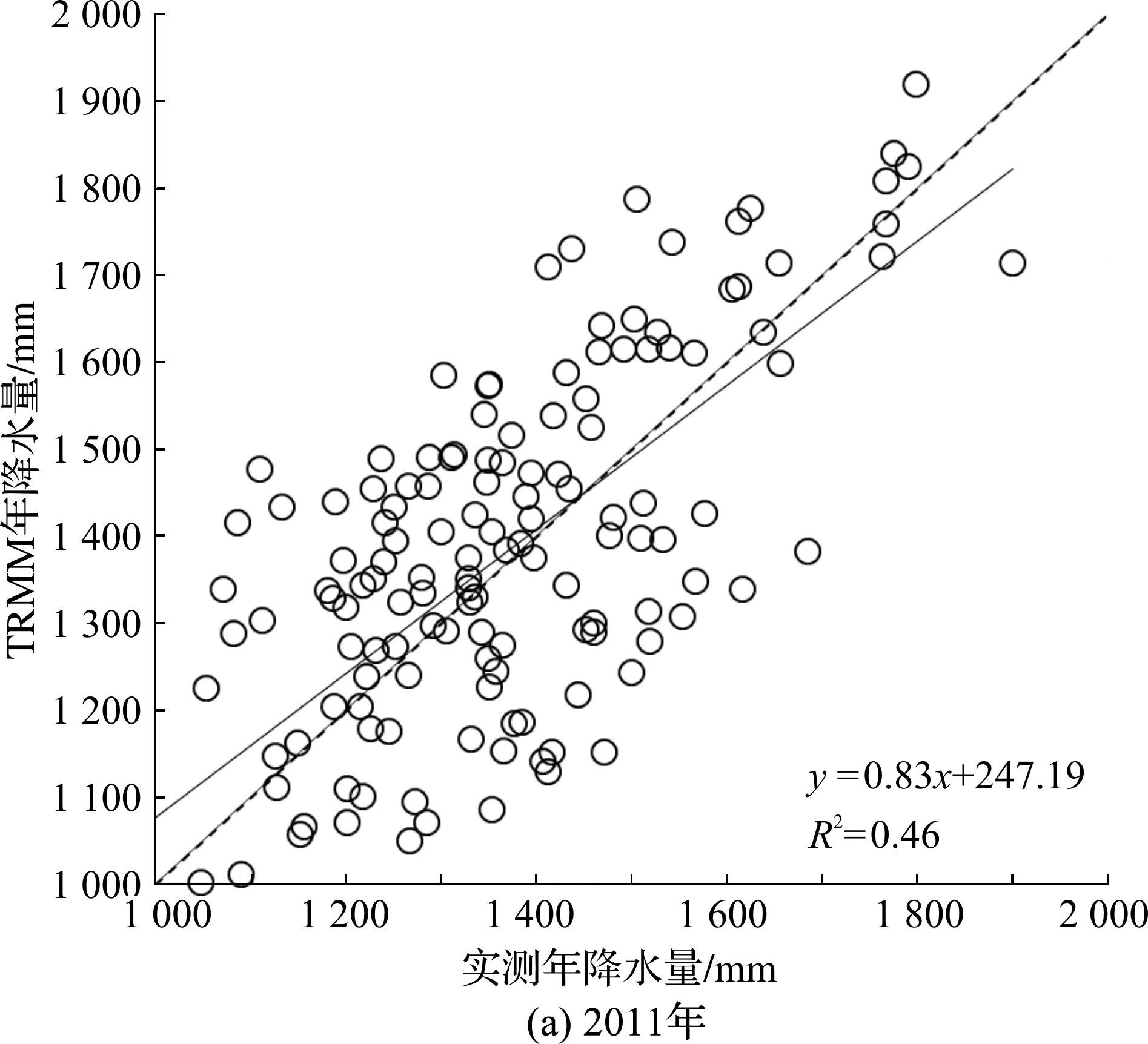
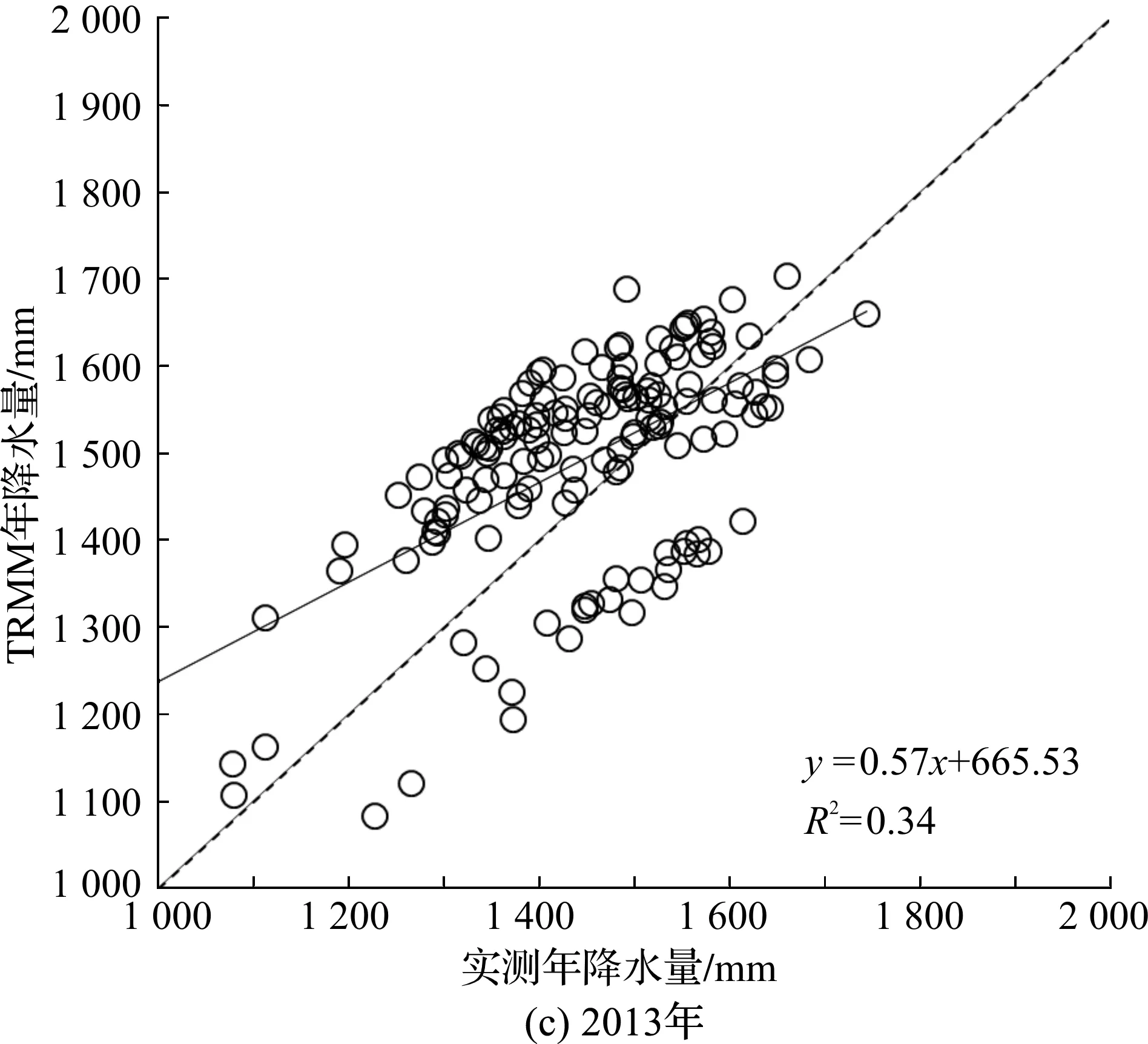
图2 2011—2013年浙江省TRMM降水数据与实测降水数据散点图

3.3.2 典型年降水数据降尺度结果

按上述降尺度操作步骤对2011—2013年TRMM降水数据与NDVI数据进行处理.得到降尺度结果(见图3～图5).结合3年GWR降尺度操作后的年降水量数据与实测年降水量数据，绘制GWR降尺度数据与观测数据的散点图(见图6).

图3～图5中，(a)为空间分辨率为0.25°的原始TRMM降水数据，可以看到它的尺度是比较粗糙的，无法满足针对研究区浙江省的降水空间分布的研究；(b)是由TRMM与NDVI构建的地理加权回归模型预测的降水数据，空间分辨率为1 km；(c)是构建模型中求得的残差数据；(d)是由预测数据加上残差数据得到的最终降水降尺度结果.

根据图6，可以了解到GWR降尺度年降水量与地面实测站点年降水量的决定系数，并能与图2中的数据进行对比分析.2011年，两者的决定系数为0.707 6，比原始TRMM数据与实测数据的决定系数高0.244 5；2012年，决定系数为0.712 3，相比增加0.256 8；2013年，决定系数为0.657 2，相比增加0.313 9.总体来说，图6中反映的3年决定系数较高，说明降尺度后的TRMM数据与实测数据的相关性很好；降尺度后的决定系数相比降尺度前有较明显的提高，说明对TRMM数据实施降尺度方法能够显著提升它的空间非平稳性的表达.

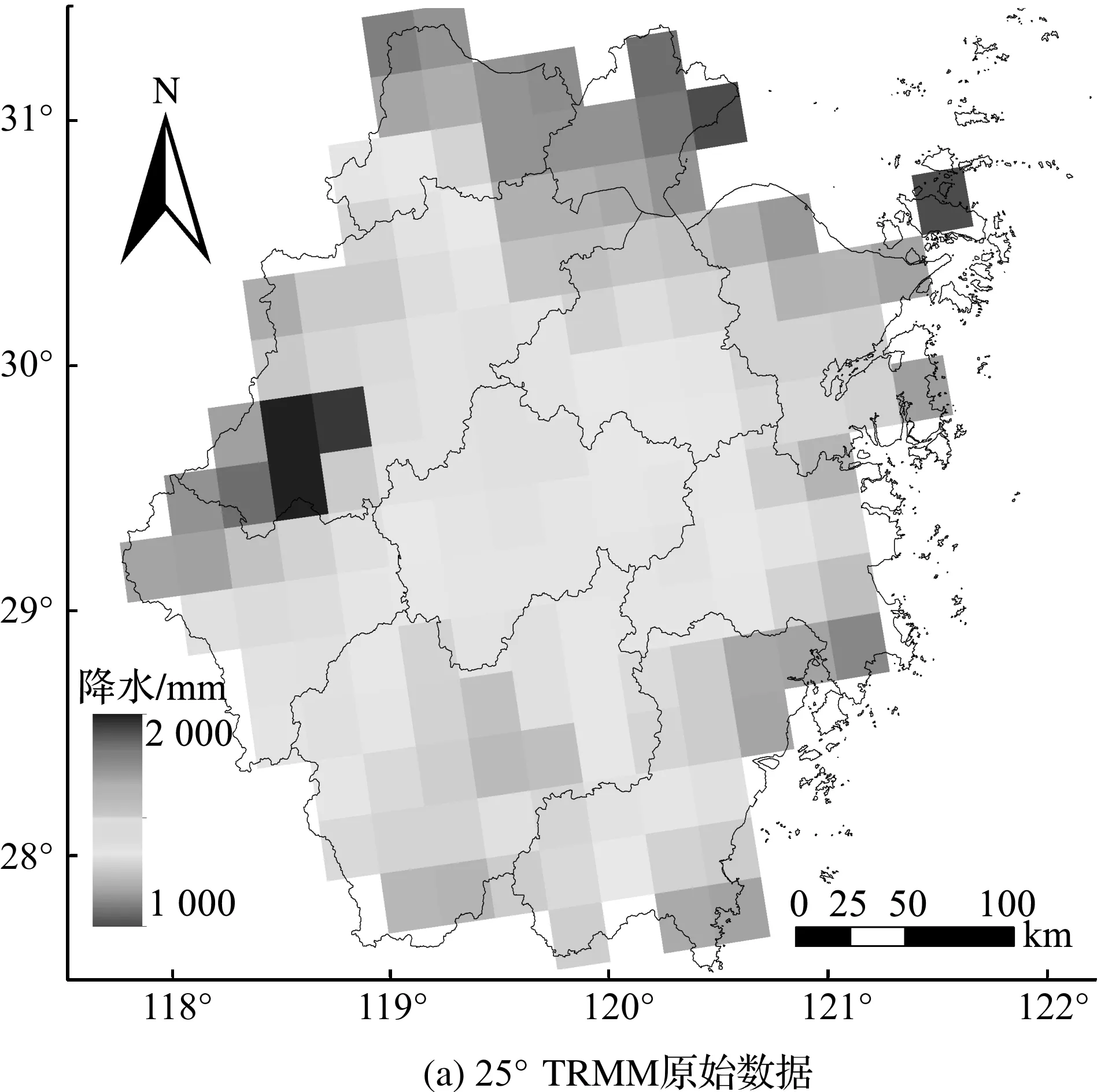
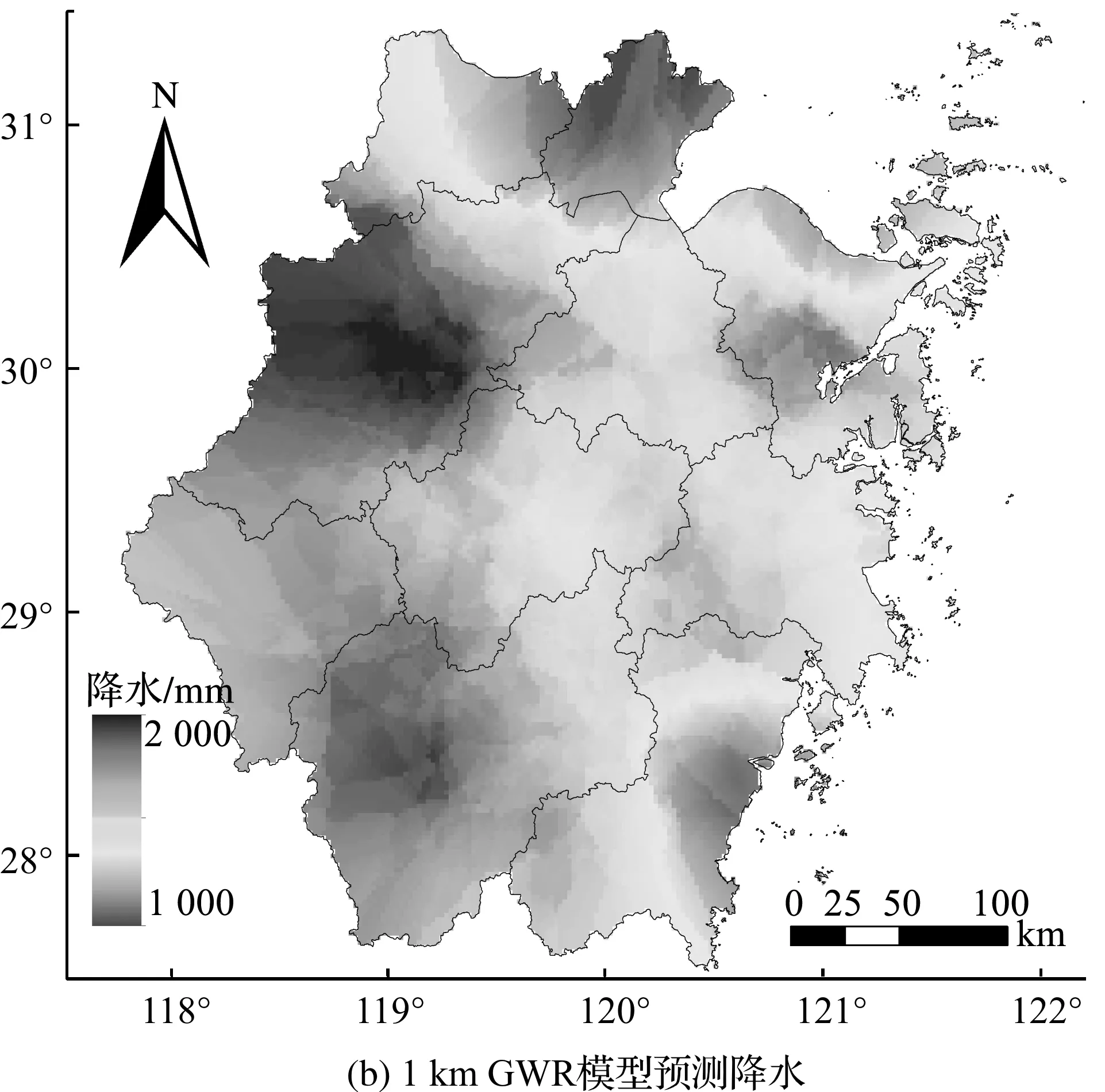
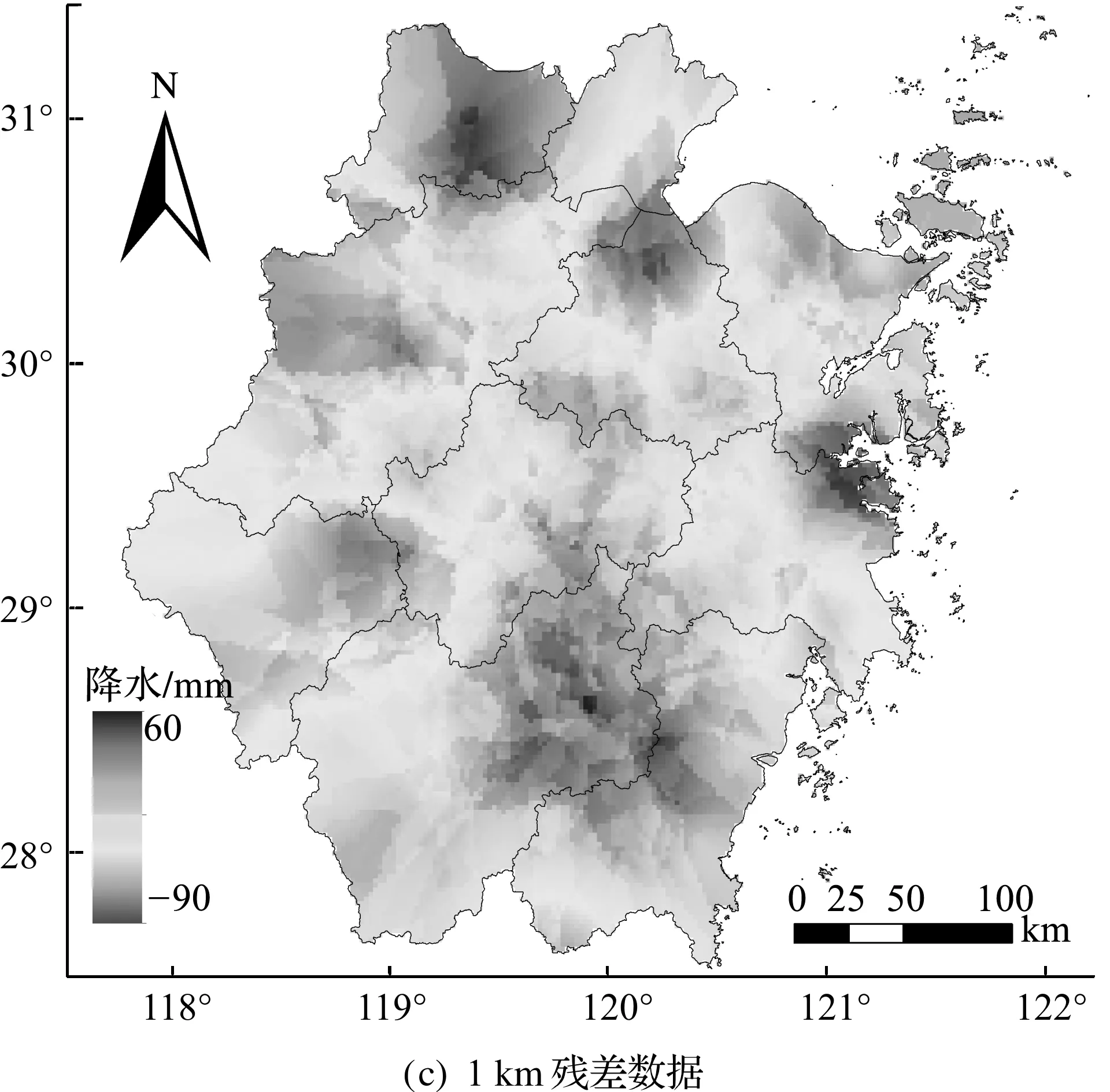
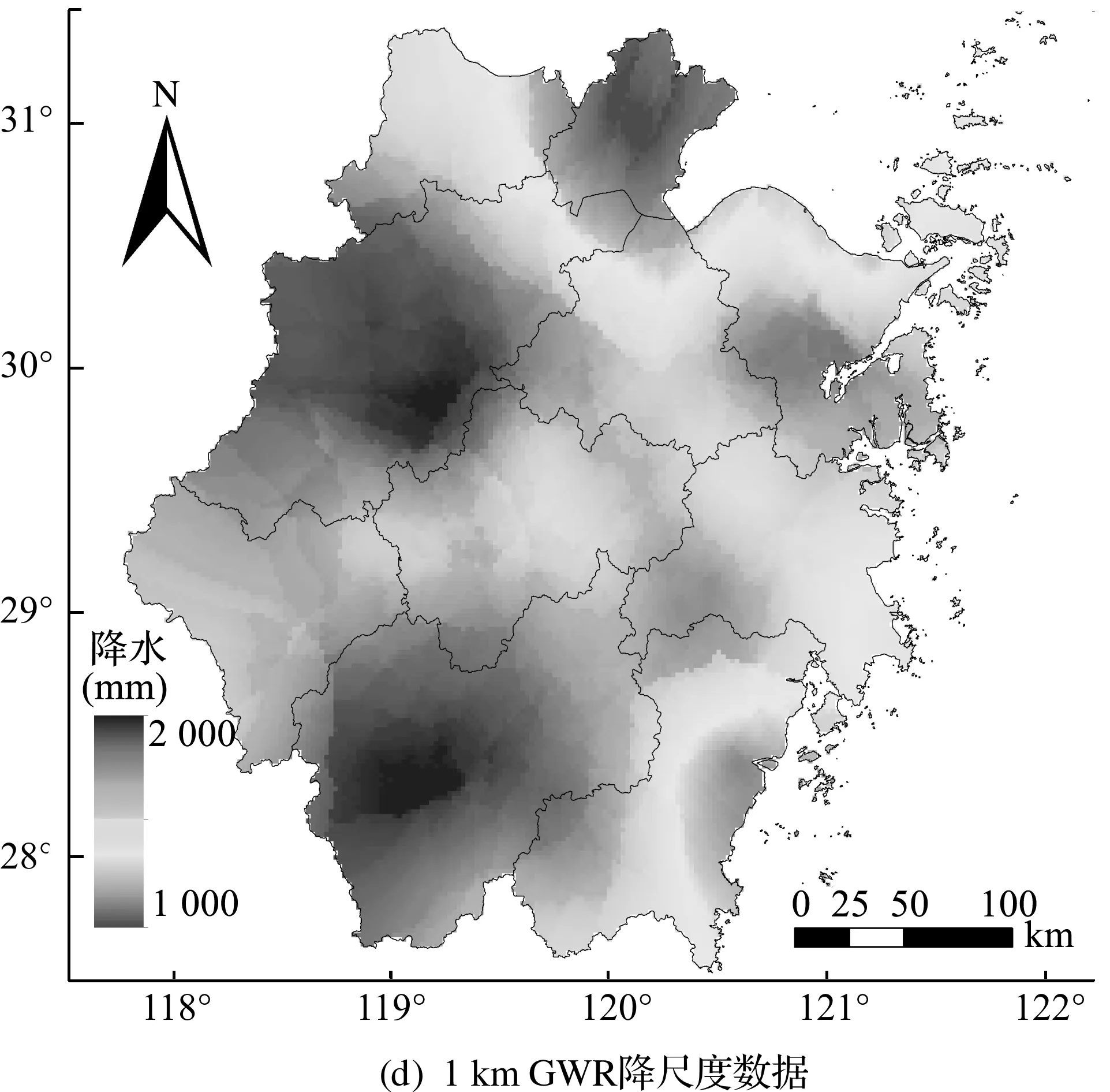
图3 2011年浙江省TRMM降水数据、模型预测降水、残差数据和降尺度数据

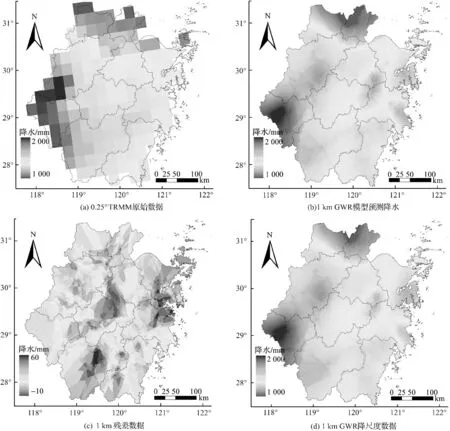
图4 2012年浙江省TRMM降水数据、模型预测降水、残差数据和降尺度数据

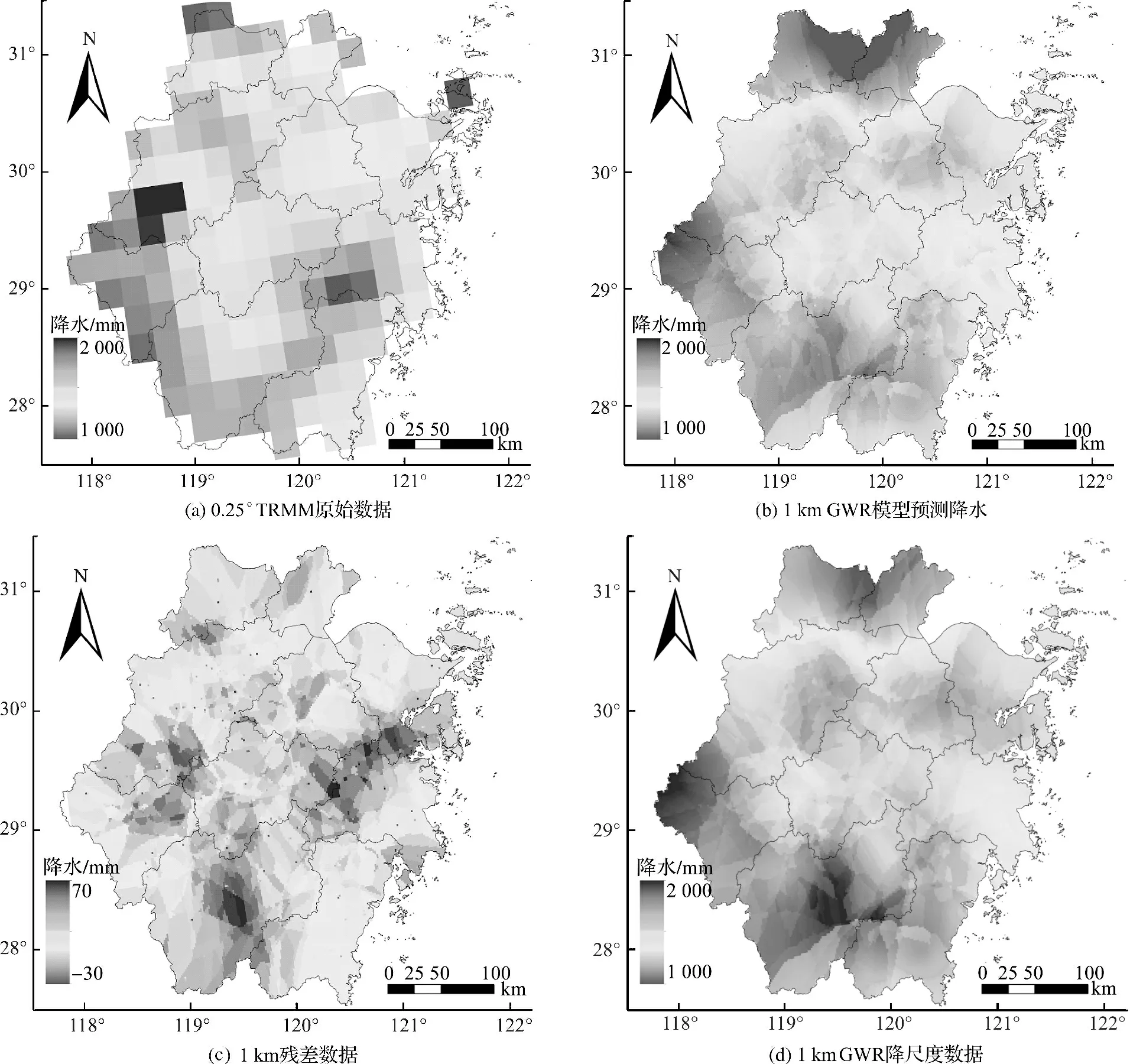
图5 2013年浙江省TRMM降水数据、模型预测降水、残差数据和降尺度数据

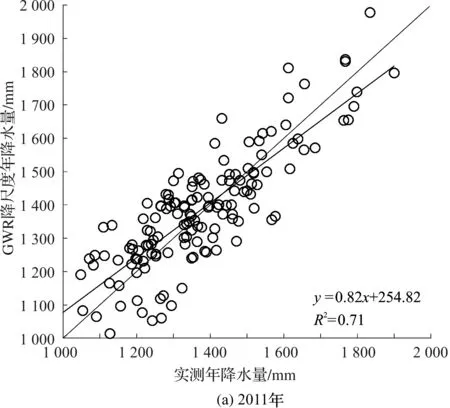
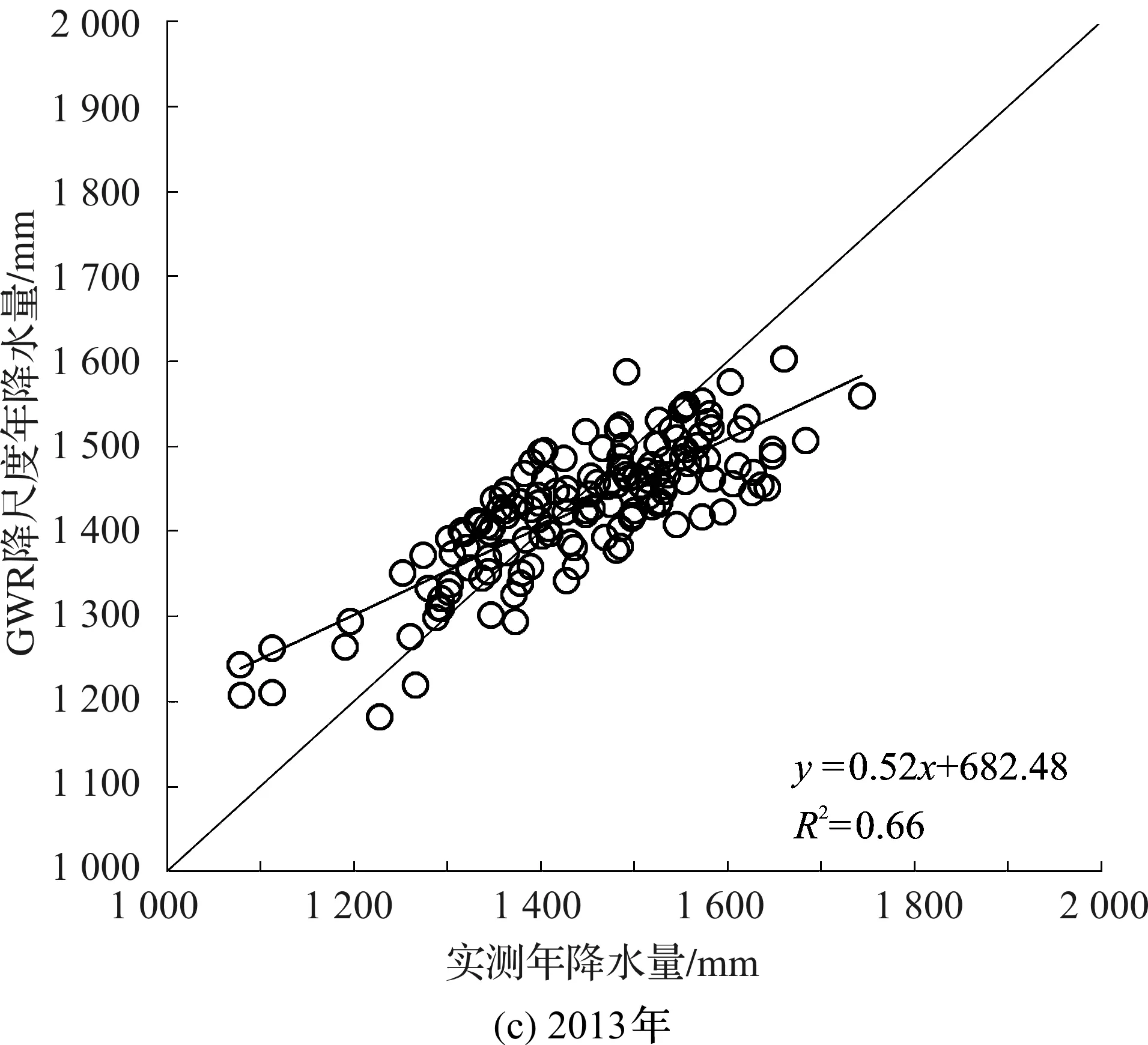
图6 GWR降尺度降水数据与观测数据散点图

3.3.3 降尺度结果与地面站点数据的比较

将进行降尺度操作后的降水数据与浙江省2011—2013年150个地面监测站点的降水数据进行结果验证.3个典型年的GWR降尺度后的降水数据与原始TRMM数据相比，同地面站点实测数据的相关系数均有可观的提升，这表明GWR降尺度方法能够使变量的空间异质性更加突出.另外，2011年GWR降尺度结果对应的BIAS降低了0.030 8，RMSE下降了63.169；2012年降尺度结果对应的BIAS降低了0.037 4，RMSE下降了54.566；2013年降尺度结果对应的BIAS减少了0.021 5，且从对结果的低估变为了高估，RMSE则减少了44.205(见表1).综上所述，利用GWR模型对TRMM降水数据进行降尺度操作可以使其与地面站点的观测数据更为接近，误差更小，与此同时空间分辨率也变得更高.

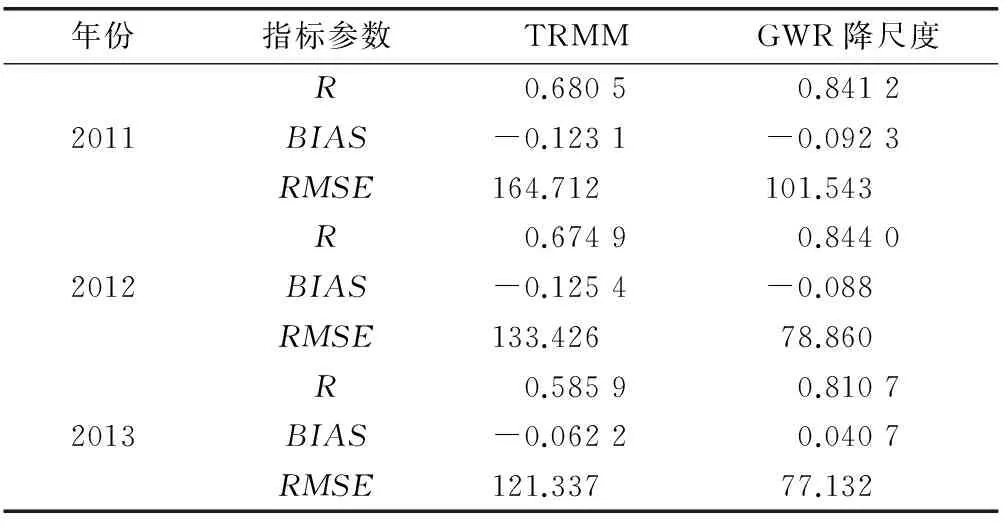
表1 降水降尺度结果验证

4 结 论

本文以浙江省为研究区域，首先结合地面监测站点数据，对2011—2013年的TRMM数据进行了精度验证，发现两者存在一定的线性相关性，且TRMM降水数据数值略大于地面站点观测值.然后以NDVI为空间因素，利用地理加权回归模型对TRMM数据进行了降尺度处理，获得了空间分辨率为1 km的降尺度降水数据，基于结果绘制的散点图显示，3年的降尺度降水数据与地面站点观测值的线性相关性都有显著的提高，说明降尺度方法可以有效地反映空间变量的空间非平稳性.最后对比了3个典型年降尺度操作前后，降水数据与地面监测站点降水数据的相关系数、相对误差和均方根误差的变化，结果显示3年的相关系数均略有提高，稳定在0.8左右，相对误差有小幅降低，均方根误差有显著的降低.因此，使用地理加权回归模型对TRMM将于数据进行降尺度处理，以牺牲一部分数据精度为代价，可以提高TRMM数据的空间分辨率，同时使其能更好地表现变量的空间非平稳性，更真实地反映降水在研究区的空间分布.

[1] Bhattacharya A, Adhikari A, Maitra A. Multi-technique observations on precipitation and other related phenomena during cyclone Aila at a tropical location[J]. International Journal of Remote Sensing, 2013,34(6):1965-1980.

[2] 郝振纯,童 凯,张磊磊,等.TRMM降水资料在青藏高原的适用性分析[J].水文,2011(5):18-23.

[3] 吕 洋,董国涛,杨胜天,等.雅鲁藏布江流域NDVI时空变化及其与降水和高程的关系[J].资源科学,2014(3):603-611.

[4] Huffman G J, Adler R F, Bolvin D T,et al. Improving the global precipitation record: GPCP version 2.1[J]. Geophysical Research Letters, 2009,36(17):153-159.

[5] Okamoto K I, Ushio T, Iguchi T, et al. The global satellite mapping of precipitation (GSMaP) project[C]//IEEE International Geoscience and Remote Sensing Symposium. IEEE,2006:3414-3416.

[6] 自 勇.GPCP与中国站点雨量计观测降水之气候比较[A].中国气象学会.推进气象科技创新加快气象事业发展——中国气象学会2004年年会论文集(下册)[C].中国气象学会,2004:1.

[7] 杨云川,程根伟,范继辉,等.四川盆地及周边地区TRMM3B42数据精度检验[J].气象科学,2013(5):526-535.

[8] 曲 伟,路京选,宋文龙,等.TRMM遥感降水数据在伊洛瓦底江流域的精度检验和校正方法研究[J].地球科学进展,2014(11):1262-1270.

[9] Ahmet Emre Tekeli,Hesham Fouli. Evaluation of TRMM satellite-based precipitation indexes for flood forecasting over Riyadh City, Saudi Arabia[J]. Journal of Hydrology,2016(541):471-479.

[10] 刘 欢,郭建平,陈田萌,等.全球热带海洋地区降水季节变化的TRMM卫星观测[J].科学通报,2017(1):90-104.

[11] 何会中,崔哲虎,程明虎,等.TRMM卫星及其数据产品应用[J].气象科技,2004(1):13-18.

[12] 王晓杰.基于TRMM的天山山区降水降尺度方法及其空间变异特征研究[D].石河子:石河子大学,2013.

[13] No-Wook Park,Chung-Ru Ho. Spatial Downscaling of TRMM Precipitation Using Geostatistics and Fine Scale Environmental Variables[J]. Advances in Meteorology,2013,2013(11):187-190.

[14] ZHENG X,ZHU J J. A methodological approach for spatial downscaling of TRMM precipitation data in North China[J]. International Journal of Remote Sensing, 2015,36(1):144-169.

[15] CHEN F R,LIU Y,LIU Q, et al. Spatial downscaling of TRMM 3B43 precipitation considering spatial heterogeneity[J]. International Journal of Remote Sensing, 2014,35(9):3074-3093.

[16] 覃文忠,王建梅,刘妙龙.地理加权回归分析空间数据的空间非平稳性[J].辽宁师范大学学报：自然科学版,2005(4):476-479.

[17] Brunsdon C, Fotheringham S, Charlton M. Geographically Weighted Regression-Modelling Spatial Non-Stationarity[J]. Journal of the Royal Statistical Society, 1998,47(3):431-443.

[18] 苗长明,樊高峰,毛裕定.浙江省降水量时空特征及近40年变化[C]//中国科协2005学术年会分会场——气候变化与气候变异、生态—环境演变及可持续发展科学研讨会,2005.

[19] 毛建生,王亚芹,林高印.基于GIS和地统计的浙江省单季稻产量和生长期降水量空间变异性研究[J].浙江水利水电学院学报,2016,28(2):48-52.

[20] 李东风,谢 峰,白福青,等.临海大田平原河网水系调整影响分析[J].浙江水利水电学院学报,2016,28(6):12-15.

Downscaling Research of TRMM Precipitation Data Based on GWR Model in Zhejiang Province

JIN Hui-ming1, XU Peng2, HE Kang3, XU Jin-tao3, MA Zi-qiang3

(1.Zhejiang Hydrology Bureau, Hangzhou 310009, China; 2.Zhejiang Yuntu Infotech Co., Ltd., Hangzhou 310053,China; 3.College of Environment and Resources, Zhejiang University, Hangzhou 310058, China)

The precipitation data of ground monitoring site and TRMM in Zhejiang Province from 2011 to 2013 are used to verify the accuracy of TRMM data. Results show that there is a significant linear correlation between observed precipitation data and TRMM data. Using NDVI data as the spatial factor, the downscaling operation of TRMM data based on GWR model is carried out. The correlation coefficient between the three typical years and the ground data is stable at about 0.8, showing good linear correlation. After downscaling operation,Rvalue increases,BIASandRMSEvalues reduce. Downscaling operation based on GWR models sacrifices part of the data accuracy. However, it can improve spatial resolution of TRMM data, and make TRMM better to show the spatial nonstationary of variables.

GWR; TRMM; NDVI; downscaling; Zhejiang Province

TV131

A

1008-536X(2017)03-0029-08

2017-02-06

金辉明(1982-)，男，浙江东阳人，硕士，高级工程师，研究方向为水利信息化与水文模型研究.