复杂桁架内力计算中的“零杆判断”

沈靠山

(浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)

复杂桁架内力计算中的“零杆判断”

沈靠山

(浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)

针对复杂桁架的内力计算，内力计算最为常用的方法有两种，即结点法和截面法，传统方法求桁架中杆件的内力，对于结点数较多或较复杂的桁架并不太适用.在特殊情况下对几种结构内力特点的分析，归纳总结了5种零杆判断方法，即利用特殊节点判断零杆、利用整体法与结点的平衡相结合判断零杆、利用截面法判断零杆、利用对称结构性质判断零杆和利用假设法判断零杆.通过归纳总结的零杆判断方法，为快速计算复杂桁架的内力提供了可靠的理论依据.

桁架；零杆；结点；结构对称性

1 研究概述

桁架是由一些短粗的直杆铰接而成，各杆所受的内力为轴向拉压力.由于其具有内力分布均匀、材料受力合理，以及采用短杆即可跨越较大空间等优点，桁架被工程界广泛采用，如在桥梁和厂房等应用[1].为确保工程结构的安全，设计过程中需对桁架中杆件的内力进行计算[2].桁架内力计算常用的方法有2种，即结点法和截面法[3-4]：结点法是取结点为隔离体，每个结点有2个平衡方程，这种方法原理简单，但逐个取结点为研究对象，求解的过程十分繁琐；截面法是取桁架的一部分为隔离体，每次可列3个平衡方程，应用截面法求内力时，同样不能随意建立平衡方程.因此，对于结点数较多或较复杂的桁架的内力计算，这两种方法都不太适用.目前，对复杂桁架的内力计算往往是通过对零杆的判断进行简化.所谓零杆，是指桁架中轴力为零的杆件.零杆可以通过计算确定，其计算方法可采用结点法和截面法，又可根据其内力的独特性，结合结构的某些特殊性质，减少大量不必要的运算.一些学者利用静定结构的局部平衡特效判断零杆，利用附属结构的性质判断零杆，利用对称结构的性质来判断零杆，与截面法相结合判断零杆，利用假设判断零杆等方法对桁架结构的零杆判断进行了研究，并得出了一些有益的结论[5-6].从对各类文献分析来看，学者们对零杆判断的研究方法较多，但给出的实例较少[7-8].为此，本文从传统结点法和截面法出发，结合具体结构对零杆的判断方法进行了归纳和探讨，并对各种方法的适用范围进行了初步研究.

2 零杆的判断方法

2.1 利用特殊结点判断零杆

在桁架中，通常有一些特殊的结点，即结点不受荷载或所受荷载较为特殊时，组成其结点的杆件往往是零杆.一般来说，常规结构根据组成的杆件数量可分以下3种情况：二杆组成的结点、三杆组成的结点和四杆组成的结点.

(1)常见的二杆组成的结点(见图1)，即无荷载作用的结点和有荷载作用的结点，两杆不共线.图1(a)显示，当结点上无荷载作用时，很显然两杆皆为零杆，即N1和N2均为0.图1(b)显示，当结点上有荷载作用，且其中一杆与外力共线，则此杆内力与外力异号等值，不与外力共线的一杆为零杆.即N1=F，N2=0.

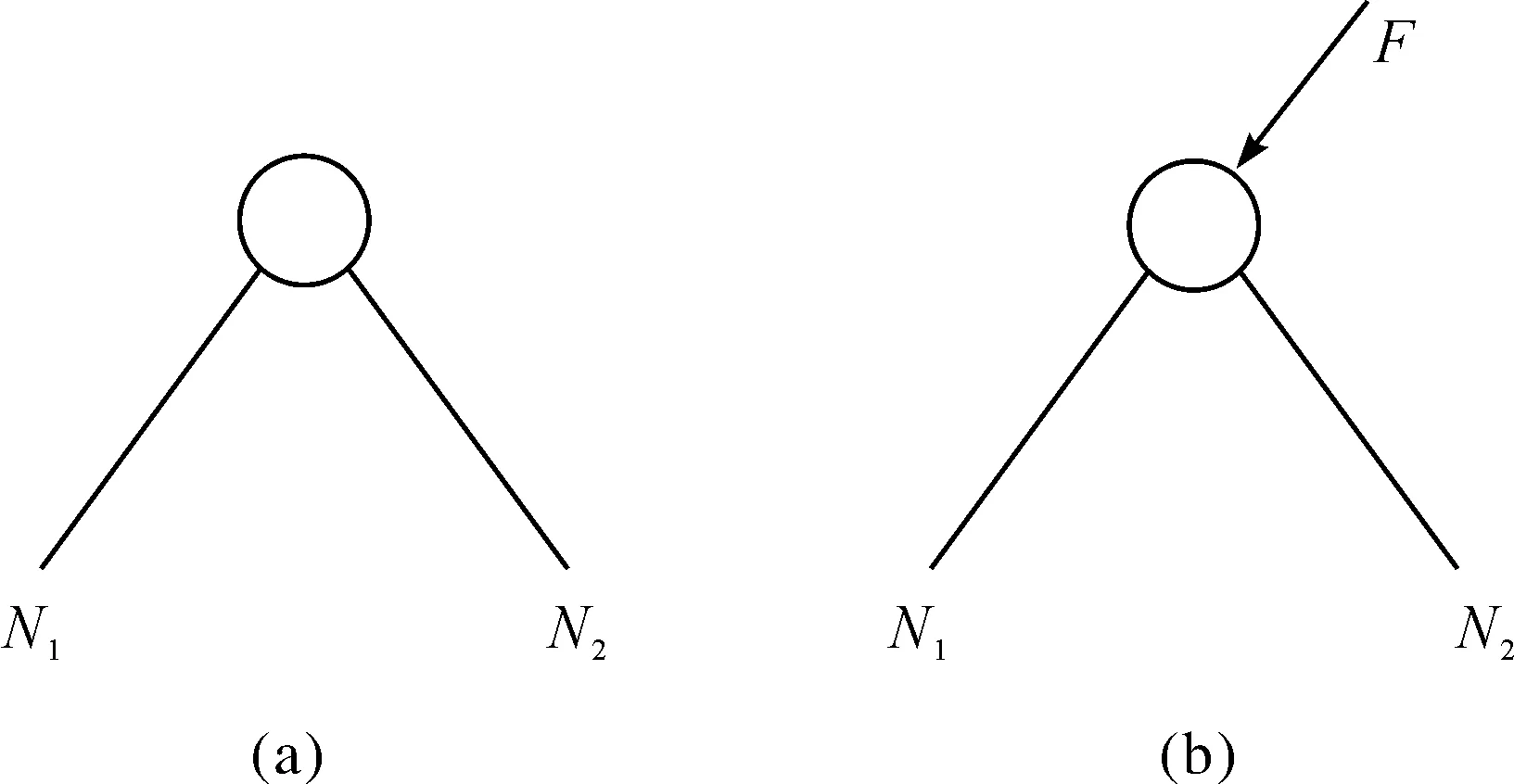
图1 二杆组成的结点

(2)无荷载和有荷载作用下，且由三杆组成的结点(见图2)，其中两杆共线，第三杆不共线.图2(a)显示，当结点上无荷载作用时，不共线的一杆为零杆，共线的两杆内力同号等值，即N1=N2，N3=0.图2(b)显示，当结点上有荷载作用，且外力与第三杆共线时，虽不存在零杆，但可直接求出第三杆的内力，即N3=F，且N1=N2.当外力与第三杆不共线时，不存在零杆，内力只能采用节点法或截面法计算.

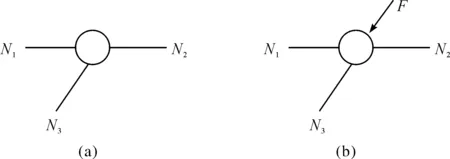
图2 三杆组成的结点

(3)无荷载作用的四杆组成的结点(见图3).四杆组成的结点只包含四个未知内力杆，且结点无荷载作用.图3(a)显示，当结点上无荷载作用时，当其中两杆在同一直线上，另外两杆在此直线同侧，且与此直线夹角相等时，两斜杆内力异号等值；对称桁架在对称荷载作用下，对称轴的此种结点无荷载作用时，该结点上的两根斜杆为零杆.图3(b)显示，当其中四杆两两共线时不一定存在零杆.但在同一直线上的两杆内力必定同号且等值，即N1=N2，N3=N4.

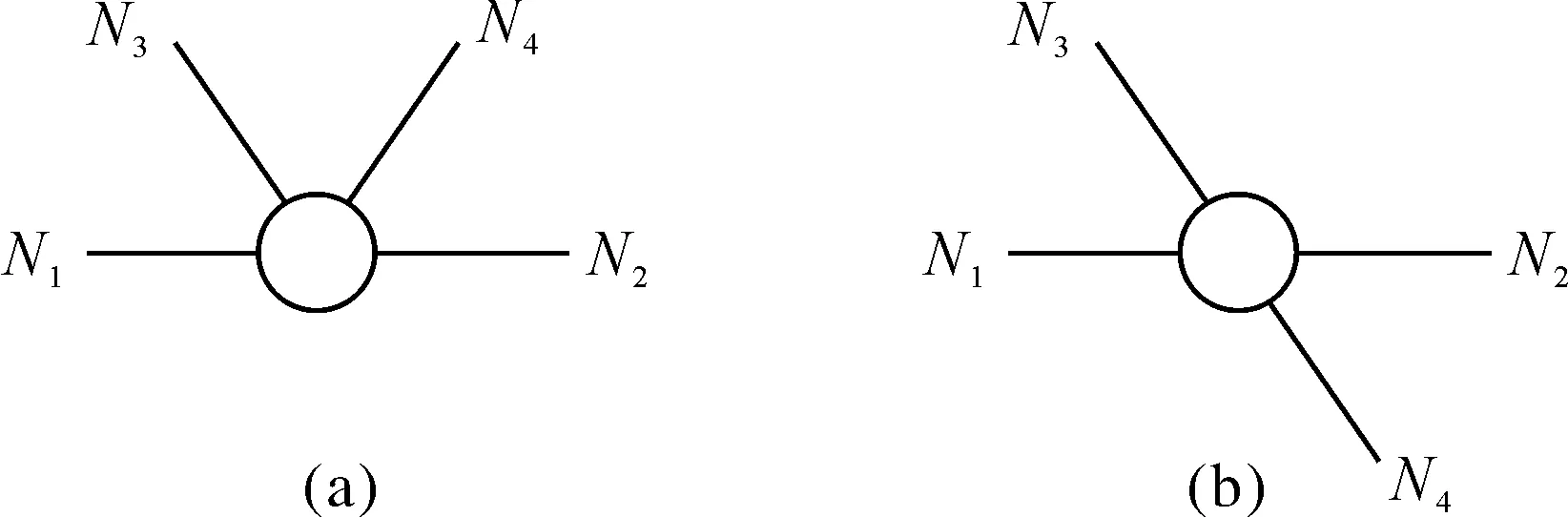
图3 四杆组成的结点

2.2 利用整体法与结点的平衡相结合判断零杆

利用结点法快速判断零杆时，往往没有涉及支座反力的求解，组成支座结点的杆件就无法判断，因此，在涉及支座结点的零杆判断时，通常先用整体法求出支座反力，再用结点的平衡判断零杆.为说明该方法，以图4给出的结构为例.

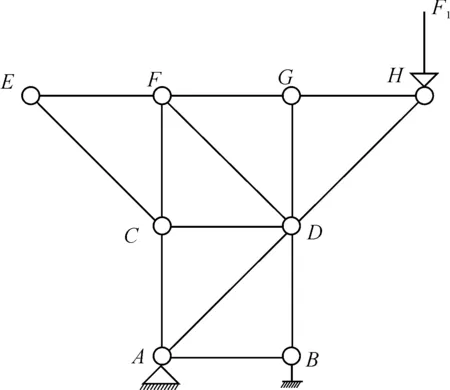
图4 带支座桁架结构

图4中，利用特殊结点可快速判断法得出杆EF、EC、CD、GD为零杆，但目前并没有完全找出零杆.然后，选取桁架的整体作为分析对象，可列出平衡方程.首先，取结点A为分析对象，利用式(1)可求出支座B的支座反力FRB，并可判断受力方向为铅垂方向.

∑MAF=0

(1)

式中：MA(F)—各分力对A点的矩.

然后，取结点B为分析对象，列水平方向的平衡方程.

∑FX=0

(2)

式中：Fx—各水平向分力.

由式(1)可得FAB=0，同理，可得FAD=0.故结构的零杆为CD、GD、EF、EC、AB、AD，共6根.

2.3 利用截面法判断零杆

有些复杂桁架结构不存在特殊结点，无法用结点法直接判断零杆，且用整体法求支座反力的过程繁琐，不便解题.对于此种桁架，可考虑采用截面法判断零杆.

一带支座的无特殊结点的桁架结构(见图5)，集中力P作用于结点F处.该方法以图5给出的结构为例，利用截面法判断零杆.

图5 带支座无特殊结点的桁架结构

图5中，I-I为截面.首先可选取截面I-I上半部分为隔离体分析，由水平方向的平衡方程，可得N3=0；其中，平衡方程表达式见式(2).然后，结合特殊结点法，可得NEA=0，NEB=0，NBA=0.因此，此结构中的零杆为杆EF、EA和EB.

2.4 利用对称结构性质判断零杆

在桁架结构中，往往存在一些对称结构，其内力通常具有以下特点，即对称结构在对称荷载作用下，内力是对称的，且反对称的未知力为0；对称结构在反对称荷载下内力是反对称的，且对称的未知力为0[3].利用对称结构的内力特点，可快速判断对称桁架当中的零杆.

下面给出实例具体说明利用对称结构性质进行零杆判断(见图6).图6(a)给出了一个结构对称的桁架，其中，水平力P作用在结点F处.由于支座A处产生了一个水平向左的力Fax，为简化计算，将荷载转化为2部分，即图6(b)所示的荷载对称作用图6(c)所示的荷载反对称作用.由图6(b)可知，结构在对称荷载作用下，反对称的未知力为0，故可得出杆FG、GC为零杆.由图6(c)可知，结构在反对称荷载作用下，正对称的未知力为0，故杆ED为零杆，从而可得出EF、DC为零杆.

2.5 利用假设法判断零杆

对于某些杆件数少的复杂桁架，可考虑利用假设法判断零杆.具体方法如下：先假设其中某一根杆件的内力方向，再利用多个结点的平衡条件，得出该杆内力方向与假设方向相反的结论，即可得出该杆为零杆.

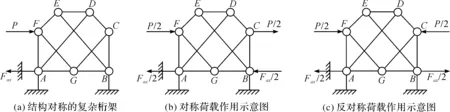
图6 具有对称结构性质的桁架结构

以图7所示的桁架为例.首先，假设NBD>0，则由B点的水平方向平衡方程，可得NBF<0，由F点的竖向平衡方程，可得NFD>0，其中，竖向平衡方程为：

∑Y=0

(3)

其中Y为各竖向分力，再由D点的水平方向平衡方程，可知NBD<0，这显然与假设矛盾，所以NBD=0.从而，NAD、NDF也为零杆，由此可得到结构中的所有零杆.

图7 带支座的复杂桁架

3 结 论

本文针对复杂桁架利用传统的结点法和截面法求解存在内力计算量大、求解过程繁琐这一问题，通过对结构在特殊结点及结构对称等情况下内力特点的分析，归纳总结出5种零杆判断法，为快速计算复杂桁架内力提供了可靠的理论依据.

[1] 孙训芳,方孝淑,关泰来.材料力学[M].武汉：武汉理工大学出版社,2012.

[2] 李晓英,杨恩伟.下承式预应力桁架系杆拱桥设计与施工[J].浙江水利水电专科学校学报,2010,22(2):58-60.

[3] 朱守芹,毕全超.浅谈静定平面桁架中的零杆判断[J].河北建筑工程学院学报,2007,25(1):102-104.

[4] 黄志刚.静定平面桁架内力计算的方法与技巧[J].中国科技信息,2014(22):84-85.

[5] 刘彩棉,邹小平.复杂桁架的内力计算[J].山西建筑,2007,33(6):80-81.

[6] 朱守芹，毕全超.浅谈静定平面桁架中零杆的判断[J].河北建筑工程学报,2007,25(1):102-104.

[7] 吴 明,丁克伟.桁架内力计算方法的讨论[J].力学与实践,2013,35(6):82-84.

[8] 林 枫,陈奕杰,詹 伟.考虑剪切效应的六边形开孔蜂窝梁挠度研究[J].浙江水利水电学院学报,2015,27(1):42-45.

Judge of Zero-pole in Internal Force Calculation of Complex Truss

SHEN Kao-shan

(Survey and Design Institute of Qiantang River Administration of Zhejiang Province, Hangzhou 310016, China)

For the internal force calculation of complex truss, there are two commonly used methods, namely node method and section method. The traditional method for internal force of the bar is not applicable, specially for the truss with many junction points or more complex structure. Through the analysis of several structural internal force characteristics under special circumstance, five judging methods of zero-pole are summarized. That is, judging the zero-pole with special node, judging the zero-pole combined the integral method with the balance of the node, judging the zero-pole by the cross section, judging the zero-pole by the property of symmetric structure and judging the zero-pole by hypothesis method. Meanwhile, these judging methods provide a reliable theoretical basis for fast internal force calculation of complex truss.

truss; zero pole; node; structure symmetry

TU321

A

1008-536X(2017)03-0052-03

2016-12-03

沈靠山(1984-)，男，江苏连云港人，硕士，工程师，主要从事水工建筑物设计及研究工作.